融合电池温度控制的混合动力汽车多目标能量管理策略

吴生宇,邓 涛

(1.重庆交通大学 机电与车辆工程学院， 重庆 400074；2.重庆交通大学 航空学院， 重庆 400074;3.绿色航空能源动力重庆市重点实验室， 重庆 401120；4.重庆交通大学 绿色航空技术研究院， 重庆 401120)

0 引言

混合动力技术是新能源技术的重要支撑，能量管理是混合动力汽车(hybrid electric vehicle,HEV)的关键技术[1]，其策略主要分为以下两类：基于规则与基于优化。基于规则的策略高效简单，适合用于工程实际。但制定规则需要大量标定时间[2-3]。基于优化的策略需要建立数学模型，通过最优控制原理进行求解，具有计算量大，计算过程复杂，实际优化结果趋于最优等特点[4-5]。其中，具有代表性的优化策略有：基于瞬时油耗率最优的等效油耗最小(equivalent consumption minimization strategies,ECMS)策略[6-7]，以及已知整个行驶工况，对全过程进行效率优化的动态规划(dynamic programming,DP)算法[8]。Yuan等[9]设计了一种采用动态规划算法确定最优油耗经济性和满足驾驶性的能量管理策略，设置了专家规则和模糊系统来满足其控制目标。解少博等[10]通过动态规划算法求解得到关于电池SOC、行程的等效因子三维图，并最终形成查表式ECMS策略，在保证能耗经济性近似最优的前提下，保持了良好的优化实效性。

目前能量管理研究中，大部分着眼于获得最佳的燃油经济性。然而在混动系统的实际使用过程中，围绕电池热失控现象开展的讨论十分必要。涉及到电池安全性问题，主要有电池温升损伤和电芯温度不一致、不均匀现象，其中温升损伤对于电池寿命的影响重大。旨在解决电池热失控问题，Zhao等[11]通过建立电化学与三维热分析模型，模拟了不同条件下电池恒流放电的热力学过程，结果表明：高倍率放电下焦耳效应产生的热量急剧增加，占到了产热的主要部分。Kim等[12]归纳了一种三维锂电池热反应模型，研究了电池热分布、热传导与散热介质，电池结构的关系，提出借助相变材料填充，并列排列等方式避免电池发生热失控。Samba等[13]验证了极耳位置对于大尺寸电池包热效应的影响，指出对称式结构的设计有利于减小欧姆热的产生，使温度更加均匀。此类研究的对象仅针对单体电池进行建模与热分析，对电池散热的优化不能反应电池与其他动力部件的相互关系，且在恒定功率的假设下进行热仿真也不能真实反应汽车实际运行的功率变化。

部分研究者将燃油经济性与电池性能参数联合成多目标优化问题。通过选定次优参数嵌入到惩罚函数的方式，或归一化目标成本，通过加权因子将多目标简化为单一目标。Tang等[14]通过引入权重系数来衡量燃料成本和电池老化成本，进而由庞氏原理对目标函数进行求解。Li等[15]建立了关于油耗和电池寿命的优化模型，在不同循环条件下设定不同电池衰减惩罚系数，采用DP算法求解该优化目标。然而，此类方法中的加权系数难以标定，无法真实反应目标之间的权衡关系或复杂的耦合情况。

本文提出计及能耗经济性与电池温升的能量管理策略。首先建立混合动力部件模型，电池温度模型。选定了影响程度较大的待优化参数，利用NSGA-Ⅱ算法得到权衡Pareto前沿。针对极端高速工况，提出基于温升反馈的电机转矩门限值调节策略。最后通过仿真与对比，验证了该方案对于电池热累积控制的有效性，评价了不同策略之间的电池热响应指标与综合油耗指标。为顾及电池温度的能量管理策略提供了一种可行性方案。

1 动力总成结构及建模

1.1 动力总成结构

本文研究对象是一款并联式插电混合动力汽车(plug-in hybrid electric vehicle,PHEV)，其动力系统布置如图1所示。运用CAN总线进行整车分层控制。整车控制器作为上层控制系统，发动机ECM、电机控制器、电池管理系统BMS等组成动力部件控制层。整车参数如表1所示。

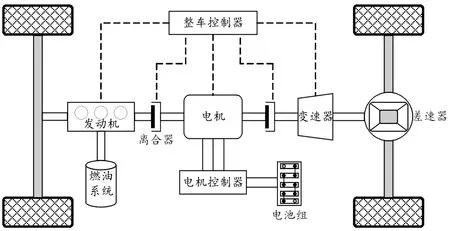
图1 并联式插电混合动力系统布置示意图

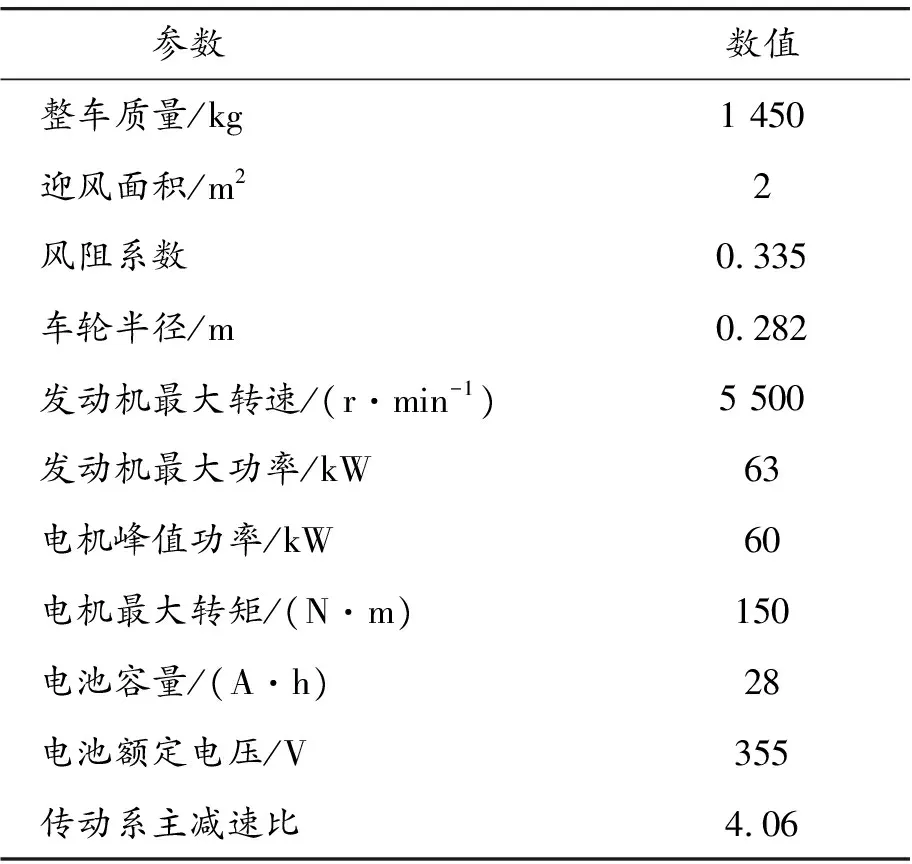
表1 整车参数

1.2 动力部件模型

1.2.1发动机模型

发动机数学模型以转速和转矩作为输入，以燃油消耗率作为输出，建立三维查表形式的MAP，便于后续的计算。其油耗MAP如图2所示。

图2 发动机油耗MAP

1.2.2电机模型

电机数学模型根据当前时刻的转矩及转速输出对应的电机运行效率，如图3所示。为简化模型，认为电机处于驱动状态时与其发电状态保持共同的运行效率。

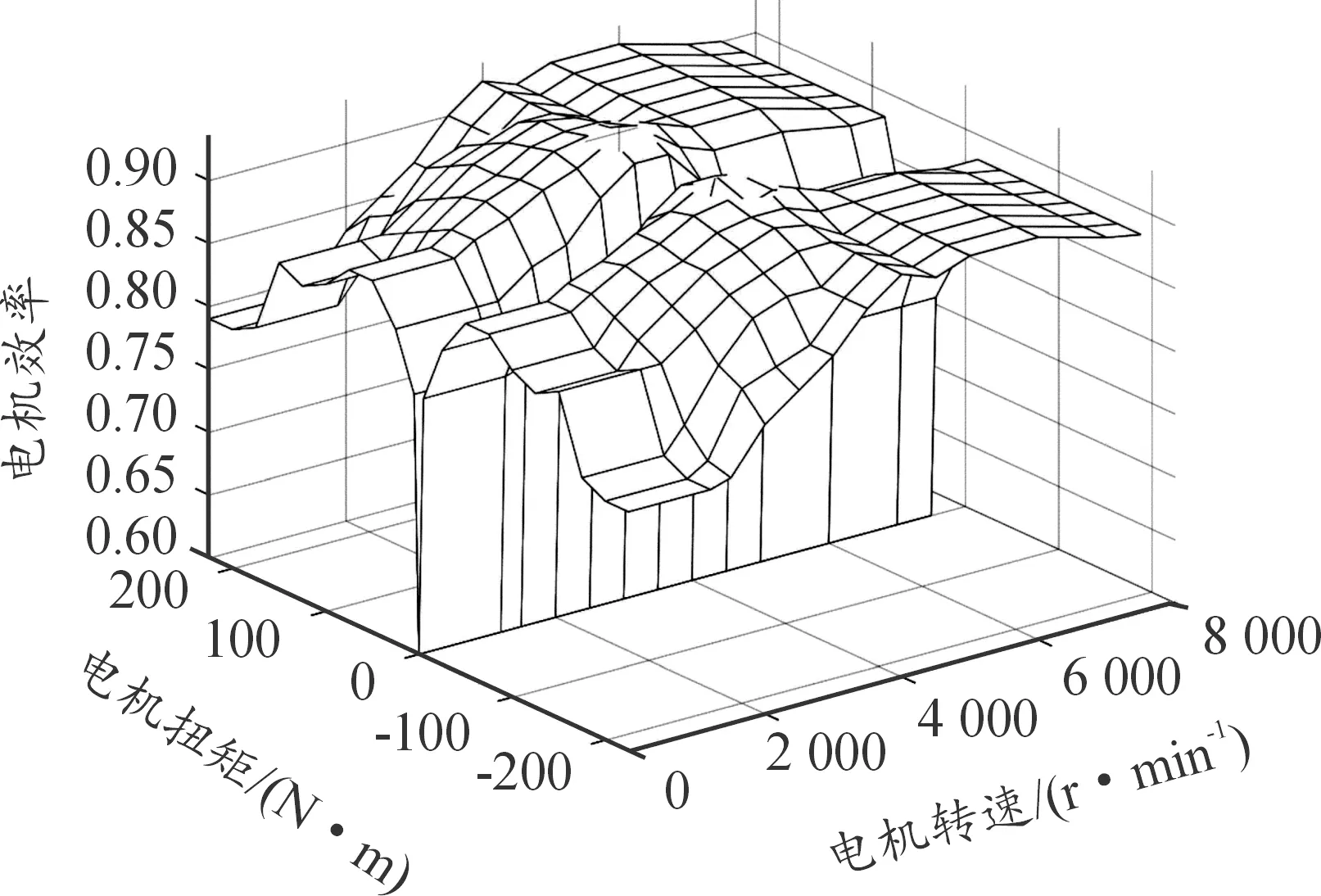
图3 电机效率MAP

1.2.3电池RC等效电路模型

为探究汽车行驶过程中电池温度的响应情况，进而实现对电池温度的主动控制。需建立能够高效反映电池内部产热与放热动态，且便于工程应用的等效电路模型。基于二阶RC等效电路建立电池模型，如图4所示。其中，OCV表示电池开路电压(open circuit voltage,OCV)；R0为电池内阻；R1和R2分别构成活化极化电阻和浓差极化电阻；C1和C2分别为对应的电容；U0为端电压；i表示端电流。

图4 电池二阶RC等效电路模型

该模型特性由下式表达：

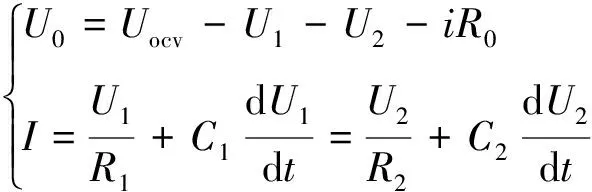
(1)

1.2.4电池热力学仿真模型

建立包含3个阶段热流交换过程的电池仿真热力学模型。第1阶段，焦耳效应在电池中产生热量。第2阶段，电池热量被传导至周围空气中。第3阶段，热量以空气对流的方式和环境进行热交换。产热过程由下式表达：

Qg(k)=i(k)2R0(k)+i1(k)2R1(k)+

i2(k)2R2(k)

(2)

假设电池表面热量以对流方式与周围空气进行热传导，在温度超过允许温度上限后进行强制冷却。任意时刻电池向周围环境传递的热量表示为：

(3)

式中:Tair为周围空气温度；Reff为有效热阻。认为电池产热的50%热量用于加热空气，空气温度Tair表示为：

(4)

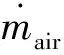
(5)

式中：h为传热系数；A表示与空气进行热传导的电芯表面积；t为模块外壳厚度；k为外壳材料的导热系数。

综上，经过3个阶段的热产生与热交换，电池温度的计算公式表示为：

(6)

式中：mbat为电池质量；Cbat为电池热容。

2 基于Pareto最优集的多目标优化

2.1 多目标优化数学表达

多目标优化问题的实质是：在约束范围之内对一系列决策变量进行求解，目标是实现待优化函数的最大或最小化。典型的多目标问题可表示为：

miny=F(x)=(f1(x),…,fm(x))

s.t.gj(x)≤0,j=1,2,…,J

hk(x)=0,k=1,2,…,K

(7)

式中：x为决策变量；m为目标个数；m组f(x)共同构成了优化空间；gj和hk组成了不等式和等式约束条件。

本文旨在设计一种具有良好燃油经济性，且电池温度保持在较低区间的混动系统。根据上述目标，建立关于燃油经济性和电池温升特性的混合动力系统多目标优化模型。

首先建立汽车油耗经济性的优化目标函数：

(8)

随后建立电池温升控制的优化目标函数，这一函数需要体现能源利用率和电池热安全。因此，以每个周期内温度升高最小化进行评价：

(9)

式中，J2为电池温升评价函数。

在满足车辆动力性和电池单次循环荷电平衡的基础上，对发动机转速ne，电机转矩Tm和转速nm，电池放电范围进行约束。发动机转速，电机转矩、转速均不能超过标定范围的最大值。电池SOC下限设置为0.2，单次循环允许的最大放电深度不得超过0.7。

综上，以燃油经济性与电池温升为优化目标的混合动力系统多目标优化数学模型为：

miny=F(x)=(f1(x),f2(x))

f1(x)=J1

f2(x)=J2

s.t. 800≤ne≤nemax

Tm min≤Tm≤Tm max

nm min≤nm≤nm max

20%≤SOC≤90%

T≤Tmax

(10)

式中：y为权衡Pareto解；T表示在整个行驶过程中的电池温度。

2.2 优化参数

在燃油经济性方面，发动机和电机的部分控制参数对耗油量影响较大。与油耗表现密切相关的参数，如发动机最大功率、发动机最高允许转矩等。在电池热效应方面，与动力电池、驱动电机相关的参数也能直接改变电池充放电电流，进而引起电池温度场的变化，如电机控制器允许的最低电压、电池SOC范围、电池充电功率等。本文选取与燃油经济性和电池温升相关程度较大的5个参数作为优化项，具体如表2所示。

表2 优化参数

3 能量管理多目标优化的实现

3.1 NSGA-Ⅱ多目标参数优化

考虑到加权法处理多目标问题的缺陷，本文采用Pareto前沿对两目标间的冲突关系进行权衡。选用带精英策略的NSGA-Ⅱ算法，在预设约束条件下对优化变量进行迭代循环，以实数编码的方式完成代码撰写后，联合Simulink整车模型进行仿真。总体结构如图5所示。首先，进行模型参数和第一代种群的初始化，对动力部件模型设置约束后将初始化种群N调配给各个部件，运行模型，仿真完成输出f1，f2成本指标。种群N包括了多个个体，所有个体完成成本计算后对其进行快速非支配排序并计算距离函数。随后，对N进行进化操作，产生子代Ns作为新一组动力部件参数输入至Simulink重新计算成本指标，得到评价值f1、f2后,将Ns和N合并在一起，对其进行排序和拥挤度计算。最后对合并后的种群进行修剪，更新种群Nt+1作为新的父代种群。在达到预设的迭代次数mgen后输出Pareto前沿，否则继续下一次迭代。

图5 仿真总体结构框图

3.2 基于比例积分法的电流控制策略

通过NSGA-Ⅱ多目标优化算法对整车油耗和电池温升的成本函数进行求解，算法迭代终止后得到Pareto权衡控制参数。上述做法从整车模型层面，对电池温升进行有效控制。然而，电池充放电过程随着实际行驶不断发生交替，导致温升累积不断加剧，特别是在极端的高速工况下，大倍率电流放电直接导致温度持续升高。此外，急剧放电引起电池SOC快速下降，会使电池内阻产生变化，进一步导致电池温度上升。

出于上述考虑，从控制放电电流的逻辑出发对电池热累积效应进行改善。直接限制电池电流较难实现，故采用限制电机最大转矩的方式。将高速工况下的电机转矩保持在一个较低的门限值，其余需求转矩全部由发动机承担。汽车能够在驾驶员需求的车速下正常行驶，电池则在较小的输出电流下进行自然冷却。在车速高于80 km/h或电池端接受到较大需求功率时，通过调整电机最大输出转矩，进而限制电流，降低电池焦耳热的累积。引入电机转矩比例系数来调节其最大输出转矩，关系式如下：

Tm0=φTm_max

(11)

式中:Tm0为电机转矩门限值；Tm_max为电机额定转矩；φ为转矩比例系数。

采用比例积分法调整φ的大小，以当前时刻电池温度作为输入量，由文献[16]得知，电池最佳工作温度范围为15～35 ℃，当电池长期工作于 50 ℃以上时，电池衰减加剧，导致其循环寿命显著下降。仿真过程中，设置温度参考点T0为30 ℃，仿真温度距离预期差值越大，调整更小的转矩比例系数，使得电池放电电流减小。φ表示为：

(12)

4 仿真与结果分析

选用新欧洲续航测试工况NEDC作为仿真工况对NSGA-Ⅱ算法进行验证，测试在Pareto前沿参数下混合动力系统的性能指标与动力表现。为了更好地凸显电池热量累积效应和电荷使用情况，连续运行3个NEDC循环，总仿真时间3 600 s。该工况下车速与SOC轨迹如图6所示。从单个NEDC循环来看，该策略下SOC轨迹较为平缓，放电深度为5.56%。中低速工况下电池放电量均匀，SOC波动不大，在980～1 150 s高速下，SOC下降较大，放电深度约为3%，仍处于可接受范围。随后50 s内，车辆进入制动回收阶段，SOC小幅度上升。

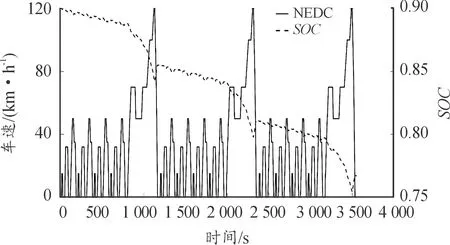
图6 车速与SOC轨迹曲线

算法达到最大进化代数后结束迭代，由整车模型输出燃油消耗和温升指标，解集最终收敛于Pareto最优解，如图7所示。该分布表明，最优前沿之间表现为非支配关系，其意义在于对经济性和温升的权衡或相互制约。不同的解则代表了对某一目标的侧重点。选取7组代表性Pareto解，如表3所示。相较于初始参数，Pareto前沿无论是油耗表现还是温升表现均优于对照值。以第二组为例，在达到循环终点时的温度比优化前降低11.12%，发动机耗油量减小了21.38%。

图7 多目标Pareto前沿图

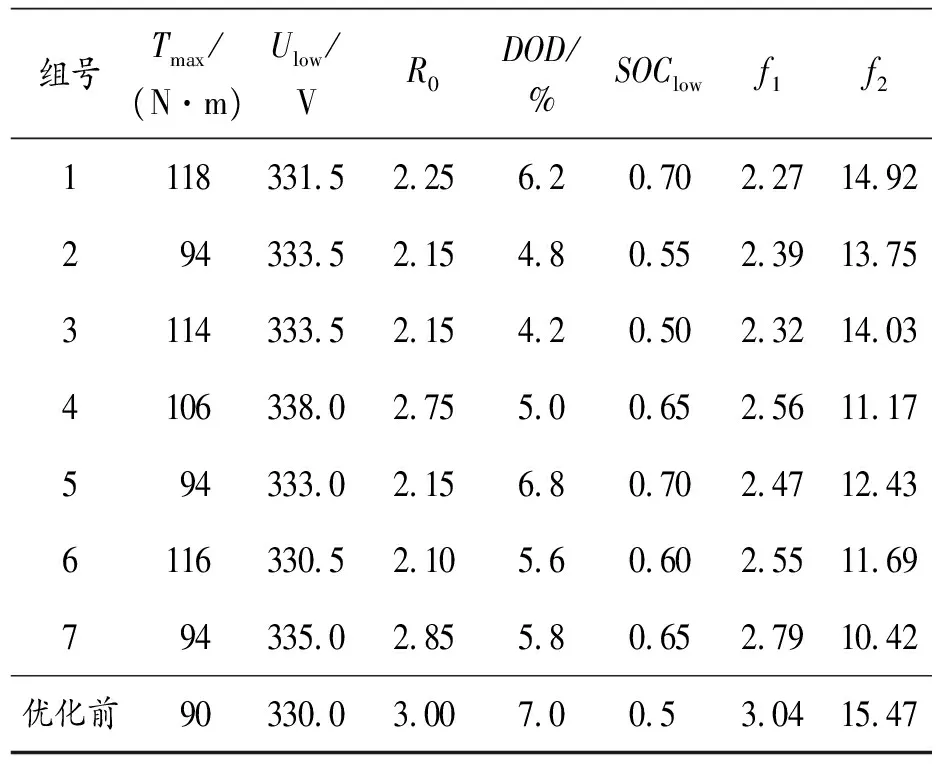
表3 部分优化参数及评价指标

为验证大功率需求条件下，引入温升反馈限制电机转矩对电流的影响效果，对参数优化后且加入PI控制策略和未作控制的电流情况进行对比，电流变化情况如图8所示，其分布如图9所示。

由图8、9可知，融合温度控制策略下的电流分布更多集中于20～40 A小倍率区间，电池在中等及以上放电区间的使用频率下降，在高于80 A的大倍率放电区间缩小至零。由此可见，对比无控制下的电流分布情况，比例积分法通过对电机转矩上限值的适当调整，良好地限制了高倍率放电电流。

图8 电流变化曲线

图9 电流分布直方图

通过分析工况循环下电池温度响应情况以及SOC变化，可直观得到多目标优化算法与控制电机转矩门限值对于控制电池温升的可行性。图10显示了在3段NEDC工况循环下电池温度的变化趋势，与之对应的各组不同的SOC变化情况如图11所示。其中，策略A：融合温升反馈的多目标参数优化；策略B：仅作参数优化；策略C：未优化。

整体来看，NEDC末段的高速工况对于电池温升的影响是显著的，仅通过多目标参数优化难以直接改善电池热累积，策略B中，电池终点温度达到为37.42 ℃，SOC下降约14%，热累积效应仍然存在，但处于可接受范围；通过增加限制高倍率区间的放电量，在策略A中电池终点温度下降至30.92 ℃，SOC轨迹呈现出更加平缓的下降趋势，降幅约为6%。这是由于限制了大倍率电流，电机使用频次远低于策略B、C，使得终点SOC高于前两者。

图10 电池温度曲线

图11 SOC曲线

最后对不同策略间的评价指标值进行对比。由于3种策略的电能消耗量截止于不同SOC点，而SOC偏差会直接影响到发动机油耗，于是采用“综合油耗成本”来衡量燃油经济性。其表达式如下：

Qtotal=cfuel*mfuel+celec*melec

(13)

式中:mfuel和melec为油耗量和电耗量；cfuel和celec则表示燃油成本和电价，分别取9/L和0.6/度。

最终评价值如表4所示，对比可知，融合温升反馈的多目标参数优化方案相较于单一的多目标优化方案在循环结束后模块温度降低6.5 ℃，相较于未优化方案降低11.55 ℃。其中，高速工况段(控制段)模块温度分别降低6.04、10.9 ℃。表明该策略不仅能有效缓和普通工况下电池热效应，还能改善极端工况下的温升情况。此外，带参数优化的能量管理策略使得综合油耗相较于优化前降低12.23%；加入反馈调节后的参数优化方案在综合油耗方面降低了3.37%，且获得了良好的限制温升效果。

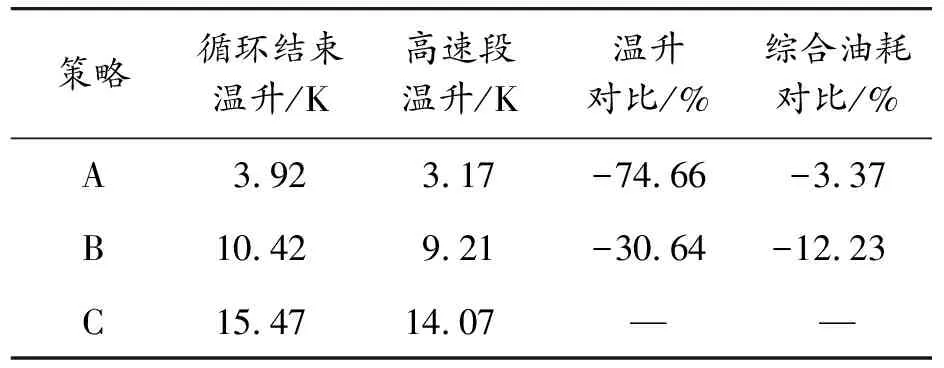
表4 3种策略评价值

5 结论

1) 提出了基于电流主动控制的多目标优化方法，综合考量整车油耗、电池温升、高倍率电流幅值控制3个因素，构建了多目标能量管理策略。

2) 结果表明：采用多目标最优参数后，电池温度指标最高降低了30.64%，综合经济性指标降低12.23%。在该条件下加入了电机转矩门限值控制策略，高速工况下进一步限制了电池产热速率，温度指标降低至74.66%，综合油耗降低3.37%。

3) Pareto前沿旨在揭示目标间的制约关系，其最优解集提供了权衡多目标问题的备选方案。今后的研究可构建由2个或2个以上电池相关指标与整车动力性能、污染物排放指标构成的多目标前沿曲面。