初中数学课堂“问题链”设计的探讨*

江苏省苏州文昌实验中学校

于永娟

初中数学课堂教学应以激发学生探究知识的动力与兴趣为主要目的.教师要以新课标的教学目标为导向，将课堂中的知识结构、数学逻辑、数学应用、学习态度等，依据数学逻辑结构构成“问题链”，通过这一教学方法满足不同能力学生学习数学知识的需求；将课堂教学内容设计成“以开阔、锻炼学生数学思维为主要任务，以知识传授为主线，以问题为纽带，以师生互动、生生互动为基本教学形式”的初中数学课堂教学方式.与此同时，设计问题链时应注意知识结构的延伸与拓展，寻找知识传授的支撑点，细化知识学习的重难点，优化知识结构的分支点，从而激发学生思维活动，加深对知识的理解与吸收，提升课堂教学质量与效果，使得初中数学教师的课堂教学工作愈加高效.

1 数学“问题链”的意义及作用

数学“问题链”是指在具体的数学知识点或知识主题范围内，以这一主题的数学学习目标及主题关键问题为教学中心，依据学生接受、理解的知识内容和经验，围绕学生在学习这一主题过程中可能会产生的问题及一些难以透彻理解的知识点，根据一定的逻辑思维、层次结构精心设计出一组既有明确目的及中心，又有层次性和阶梯性的问题.课堂上教师有目的性地提出疑问，设立障碍，布置迷局，揭晓矛盾，为学生创造更多参与数学活动的机会，帮助学生通过自主探究和合作讨论，更好地理解和掌握数学理论知识、框架结构、数学技能，深刻领悟数学思想与思维逻辑，从而丰富学生参与数学学习活动的经验，使得学生激活数学思维，深刻理解课堂所学知识，有效提高初中数学课堂教学质量与效果，促进教师教学目标的高效完成.

在初中数学教学课堂中，传统教学理念下的教学课堂，教师占据课堂主导地位，拥有绝对权力，以教师讲、学生听为主要教学手段，重视知识讲授，重理论轻实践，这种学习模式下，学生一味被动接受知识，教师的讲授几乎占据了课堂全部时间，学生缺少独立思考的时间，严重阻碍了学生数学思维的发展和探究能力的提升；同时，教师多围绕考试重点进行授课，教学内容枯燥无味，课堂气氛沉闷，师生关系紧张，导致学生对数学的兴趣大幅度降低，很难提起精神认真听讲，导致学生丧失对数学学科的学习兴趣和学习积极性，极大影响了数学教育工作的开展.而教师运用以学生为课堂主体的“问题链”教学模式，极大地激发了学生的学习积极性，推动学生积极参与课堂问题讨论，从而使得学生的数学素养得到不断提升与发展.

2 初中数学课堂“问题链”的设计原则

在初中数学课堂中，由于教师注重基础知识的学习，常常依据基础知识点设计问题，大部分学生往往能很快理解基础知识点，并且能较为轻松地解答问题，因此，会产生一种数学很简单的错觉，从而减少对基础知识夯实和拓展的钻研.然而课外练习的难度较课堂中教师设计的题目难度提升许多，对学生知识的理解程度要求也增加不少，学生完成作业的难度极大.所以，教师在课堂中应用“问题链”教学模式时，应注意“问题链”的设计方法，遵守设计原则.

2.1 设计时关注重难点知识

数学的重难点知识是以基础知识为根基，在此之上的延伸与拓展，能够打破学生认为课堂教学问题简单的错误印象，让学生产生认知上的冲突，使得学生认真对待数学知识，深刻思考重难点，不断加深学生对数学理论知识的理解与吸收.

2.2 设计时布置陷阱

由于许多学生在做数学习题时难以认真审题，很难清楚判断出题目的考点，只凭主观臆断，快速阅读题目进行解答.然而大部分数学题目都存在着隐形条件，极具迷惑性，因此，学生们极其容易掉进命题者的陷阱里.

因此，教师在设计“问题链”时，要充分利用学生在习题中发生的错误与存在的问题，有针对性地设计存在陷阱的题目，以此帮助学生通过课堂问题意识到审题时存在的不足，并通过错误来强化对知识点的理解与内化吸收，总结解题方法，提高学习效果.

2.3 注意问题的发展性与层次性

初中数学课堂中设计“问题链”时要注意以全班学生的知识水平为基础，从学生的认知结构出发，依据发展性原则，设置符合学生思维理解能力发展水平且具有一定难度的问题，以此拓展学生的思维能力，从而更好地促进学生的全面可持续发展.

案例2在学习“勾股定理的逆定理”时，教师可布置题目：

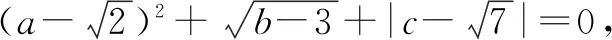
本题考查了学生对于非负数的性质和勾股定理的逆定理的掌握情况，让学生开拓思维.

此外，初中数学教师在设计“问题链”时，要尊重个体间的差异性，不能歧视或轻视认知能力较差的学生.设计的问题应遵循“由易到难、由浅入深、由现象到本质、由抽象到具象”的原则，设计具有层次性的问题，使得不同认知水平的学生在课堂中有时间去思考、探究；同时，注重发散学生思维，通过数学解题技巧的迁移运用，达到举一反三的效果，使学生学会从多个角度思考问题，清晰数学知识的脉络体系，创建数学知识的理论框架.

3 初中数学课堂“问题链”的设计策略

3.1 设计“问题链”要找到知识传授的支撑点

初中数学课堂教学既要注重学生的数学基础知识，又要掌握学生的认知水平和学习能力、理解能力.因此，教师在设计“问题链”时要找到知识传授的支撑点，综合考虑题目的难度、有效度、思考度，以此激发学生思维能力，极大地提升学生的学习兴趣，有效促进对所学数学知识的掌握及理解，有利于学生学习效率的提高.

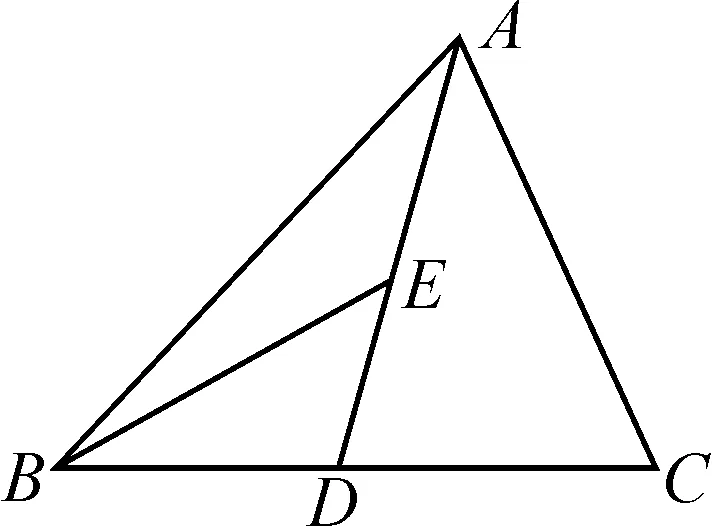
图1

案例3如图1所示，AD为△ABC的中线，BE为△ABD的中线.

(1)若∠ABE=15°,∠BAD=40°,求∠BED的度数；

(2)在△BED中作BD边上的高；

(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少？

这道题的设计意图是让本节课的知识点基于学生的认知基础，难度层层递进.

第(1)问考查相交线中邻补角的知识点.邻补角∠BED与∠BEA互补，即可知∠BED的度数.

第(2)问考查垂线的定义.高即为垂线，所以只需以E为起点，作一条与BD的延长线BC垂直的线段，即为△BED中BD边上的高.

第(3)问考查相似三角形的性质.由于BE为△ABD的中线，因此过点A作BC的垂线线与过点E作BC的垂线段之比为2∶1，通过计算可知答案.这一问题便是以三角形的知识为支撑点，不仅能够激发学生的学习兴趣，还能激起学生对于数学学习的主动性，提供给学生参与数学探索活动的机会，促使学生加深对三角形有关知识的理解.

3.2 设计“问题链”要注重学生自主学习的参与度

自主学习能力对学生的学习以及发展极其重要，它是个体在社会中极具竞争力的一种能力.因此，教师要加大对学生自主学习能力的培育力度，提高学生自主学习的参与度.教师在数学课堂教学时，应设计不同层次的问题链，使得每个学生都能积极参与问题思考，于学习探究中收获知识.

3.3 设计“问题链”要拓展学生思维的广度及深度

思维以问题为基础.教师要设计开放性、包容性较强的“问题链”，以问题为纽带，贯彻课堂教学过程，帮助学生养成学习思考、不断探究的好习惯，使得学生学习具有自主性.

在初中数学教学课堂中，教师要改变传统教学模式，应以问题为课堂教学的纽带，围绕教学目标设计问题链，此外，设计问题时应注重问题设计的原则，着力培育学生数学思维能力和解决问题的能力.