用于微低重力模拟装置的主动补偿控制方法

权宇超 兰 超 韩大鹏* 王兆魁

(1.福州大学机械工程及自动化学院, 福州 350116; 2.清华大学航天航空学院, 北京 100084)

1 引言

嫦娥五号的采样返回标志着中国探月工程规划中“绕、落、回”中的第三步已经完成,中国探月计划将进入载人深空探索阶段。 近年来,研究人员对载人探月的基础技术进行了广泛研究[1-3]。

载人探月活动需要对航天员进行针对性的训练,帮助其适应月面环境。 目前,航天员在地面模拟微低重力的方法主要有悬吊法[4]、抛物线飞行法[5]和水浮法[6],其对微低重力的模拟效果均不理想。 悬吊法精度较低,只有当绳索直线经过被悬吊体质心时才能完全平衡重力影响,否则无法平衡重力所产生的力矩;抛物线飞行法持续时间短,且无法模拟空间中的地形和安放空间站模型;水浮法水槽的造价昂贵,使用和维护成本高,且由于水的动态阻尼和粘滞效应,航天员在水槽中的运动特性与其在真实微低重力环境下的表现差异很大。 针对上述各种方法的不足,马欧等[7-11]提出了一种被动式低重力模拟系统,该系统机构重力势能及航天员重力势能与弹簧系统弹性势能可以相互转换并保持总能量守恒,实现任意位置的失重模拟,具有灵活性高、成本低、安全性好且重力可调等优势;王兆魁等[12]对以上装置进行了改进,模拟重力连续可调,调节过程简单,装置占地面积小、易部署,能够以较简单的结构达到较高的模拟精度,并对该装置关节上存在的摩擦力设计了补偿方法,弥补了摩擦力带来的微低重力模拟精度的损失[13]。

但摩擦力并不是影响该类装置微低重力模拟精度的主要因素。 装置中的弹簧刚度通常难以选取到理想值,实际采用多根弹簧构成弹簧组来代替理想刚度弹簧,而一般弹簧组的总质量可达几十千克,其质心位置会随着装置末端运动而改变,从而对失重模拟精度产生较大的影响。 此外,机械装置运动杆件不可避免的存在惯性,其对重力模拟过程中模拟精度的影响也远大于摩擦力。 进一步讲,摩擦力可通过润滑等方式进行有效抑制,但弹簧重力和惯性力的影响难以通过外部措施或被动方式消除。

针对以上问题,本文采用附加力补偿策略进行主动补偿。 在关节处安装补偿电机,建立外加电机后装置的动力学方程,在电机提供的角位移测量值的基础上,设计速度观测器和加速度观测器,给出一种惯性力及弹簧重力补偿模型,对惯性力和弹簧重力进行主动补偿,有效提高微低重力失重模拟精度,增强航天员微低重力模拟的沉浸感。

2 主动补偿原理

微低重力模拟装置参数设置如图1 所示,其中2 个弹簧刚度分别为k1、k2;2 个平行四边形杆的质量分别为m1、m2,其连接件质量(包含主动补偿装置质量)为m3,人机接口质量为m4,航天员质量为ma;第一个平行四边形关节铰中心高度为h1,两平行四边形上下连杆距离为h2,弹簧上端连接点距两平行四边形关节铰中心距离分别为d1、d2,人机接口与航天员的距离为d3,平行四边形杆长分别为l1、l2,杆质心与杆转动关节点距离分别为a1、a2;平行四边形关节转角分别为θ1、θ2,两弹簧质量分别为mk1、mk2。

图1微低重力模拟装置参数Fig.1 Para meterofmicrogravitysimulationsystem

系统的总势能主要由机构的重力势能VM、航天员的重力势能VB和弹簧的弹性势能VS组成,取失重效果为ρ(航天员被补偿重力与在地球所受重力之比),可知系统总势能VT如式(1)所示[11]:

为保证系统的总势能不随航天员的运动状态而改变,需满足条件Ci=0(i=1,2) ,基于此可解出弹簧刚度的选择条件如式(2)所示:

主动补偿系统的配置如图2 所示。 2 个主动补偿单元安装在平行四边形的2 个关节处,每个单元的组成如图3 所示,主要由伺服电机、滑环、传动齿轮、减速机、编码器等组成。 伺服电机带动传动齿轮输入端旋转,传动齿轮输出端连接减速机输入端,减速机输出端连接被补偿关节。 当编码器将关节角位置信号传输到控制器后,控制器给出对应的补偿力矩,从而抵消惯性力及弹簧重力对低重力模拟装置模拟精度的影响。

图2 主动补偿系统Fig.2 Active compensation system

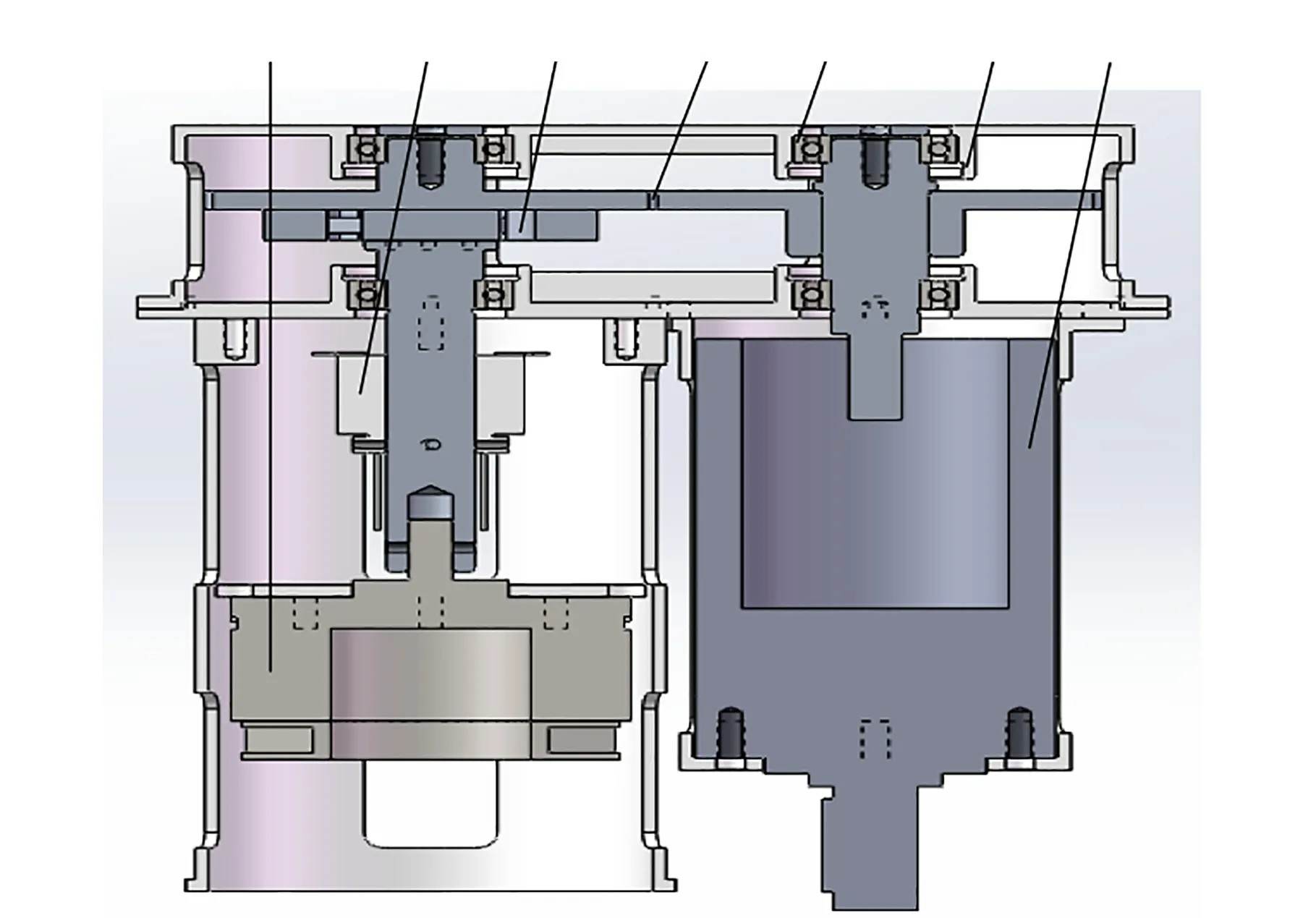
图3 主动补偿装置结构Fig.3 Structure of active compensation device

将主动补偿装置与原平行四边形系统统一考虑,根据第二类Lagrange 方程法可导出考虑弹簧重力的模拟装置动力学模型,见式(4):

式中,I1、I2为2 个平行四边形机构的转动惯量,杆件长度中间变量如式(7)和(8)所示:

由此建立了考虑系统中主动补偿装置及弹簧重力的动力学方程。 基于方程中的M(θ)θ¨项及Gk(θ) 项中的弹簧重力矩,通过θ、θ·、θ¨值以及各杆件参数可实时计算得到弹簧重力及惯性力,从而得到所需的附加力矩值,该力矩值由伺服电机提供,进而就可以实现主动补偿。

3 补偿控制策略

本文采用一种可在线进行装置惯性力和弹簧重力补偿的计算力矩法实现微低重力装置的主动补偿。 其基本思路为[14]:在内控制回路中引入非线性补偿,且惯性力项和重力项包含在该非线性补偿中,将系统变为易于控制的线性定常系统。对于装置惯性力的二阶非线性,在实际装置中无法通过安装传感器测量,本文通过加速度传感器来观测系统的角加速度,从而求得在系统运动过程中产生的惯性力及重力。

3.1 三阶观测器设计

受空间限制,主动补偿系统只安装有位置测量单元,考虑到惯性力的二阶非线性使其在实际中无法测量,需通过加速度观测器观测模拟装置的加速度,从而得出模拟装置在运动过程产生的惯性力。 将模拟装置的动力学模型(4)改写成状态空间方程,如式(9)所示:

3.2 主动补偿策略

主动补偿策略如图4 所示。 编码器实时测量模拟装置的各关节转角信息,并以脉冲的形式发送给解码器,解码器将关节转角信息分别发送给弹簧重力补偿模型、惯性力补偿模型来计算出对应的平衡力矩,然后将得到的力矩信息实时发送给模拟装置的各关节电机,使电机输出反向驱动力矩来抵消模拟装置因动力学特性而产生的附加力矩,从而实现模拟精度的提升。

图4 主动补偿策略控制框图Fig.4 Block diagram of active compensation strategy

关节电机的补偿力矩τm如式(11)所示:

式中,τG为补偿的重力力矩,τI为补偿的惯性力力矩,结合动力学模型(4)与式(10),补偿力矩取值如式(12)、(13)所示:

4 试验验证

为有效验证模拟装置的性能,选取合适的弹簧组和对应的丝杠高度模拟航天员在月球环境下的重力水平(ρ=0.83)。 被试人员的躯干固定在微低重力模拟装置的末端,在跑步机上模拟月面的跳跃运动。 对应的试验验证系统如图5 所示。

图5 主动补偿装置安装实物图Fig.5 Installation diagram of active compensation device

模拟装置的各项物理参数如下:m1=5.73 kg,m2= 5.73 kg,m3= 15.78kg,m4= 18.13 kg,ma= 75kg,mk1= 19.88kg,mk2= 11.7 kg,l1=1 m,l2=1 m,a1=0.5 m,a2= 0.5 m,h1=1.68 m,h2= 0.45m,d1= 0.6m,d2= 0.4m;被试人员体重限制在70 kg。 试验过程中被试人员重心的初始位置为xa= 1.32 m,ya= 1.4m;式(10)中参数设置为Λ1=diag(5,5),Λ2=diag(5,5),Λ3=diag(5,5) 。

图6、图7 分别给出了2 个关节上的位置测量值和观测器给出的的速度和加速度值。

图6 关节1 运动参数观测值Fig.6 Observation of joint-1’s the motion parameters

图7 关节2 运动参数观测值Fig.7 Observation of joint-2’ s the motion parameters

可以看出,速度和加速度的噪声水平保持在较低水平,远远低于经差分计算得到的速度和加速度值,显示动力学模型参与式(10)中观测器计算的良好效果。

图8～10 依次给出了被试人员在重力方向的加速度、速度和位置变化曲线。 为了进行比对,采用同样的物理参数进行了仿真,图中给出了主动补偿前、主动补偿后和理想条件下的曲线对比。

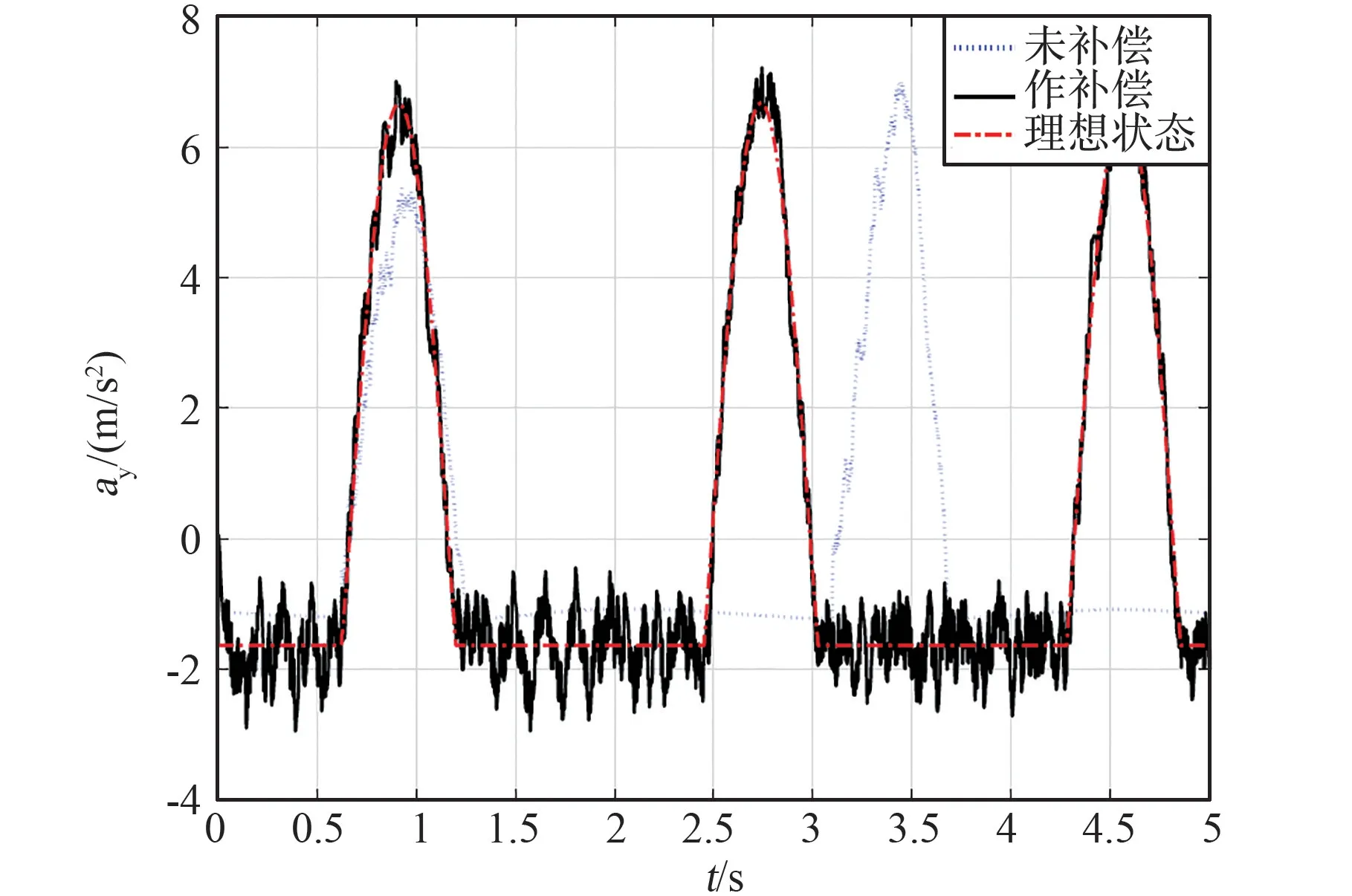
图8 被试人员y 方向加速度Fig.8 Acceleration of test subjects in the y direction

图8 表明,未进行补偿时,由于弹簧组重力的存在,下落阶段加速度不是月球的重力加速度1.633 m/s2;且由于机构惯性力的存在,下落阶段(1.4～2.4 s 区间)加速度不恒定,即机构会对被试人员产生持续拉拽。 在进行主动补偿后,在下落阶段可实现月球重力加速度,部分缓解了机构对被试人员的拉曳,局部改善了对月球跳跃的模拟,但由于加速度有跳变,改善效果尚不能持续,这是主动补偿面临的最大难题。 从图9～图10 可知,未进行补偿时,弹簧组重力与机构惯性力会使被试人员的运动滞后,且随着时间的推移,滞后在不断地扩大。 在进行主动补偿后,被试人员运动滞后性得到改善,运动状态与理想状态较为吻合,能够较好地模拟月球跳跃运动。

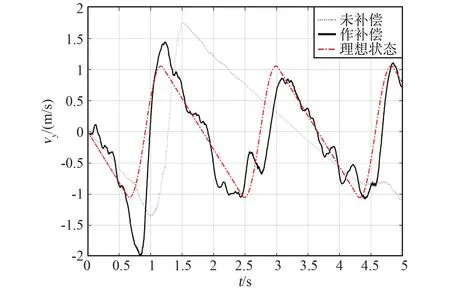
图9 被试人员y 方向速度Fig.9 Velocity of test subjects in the y direction

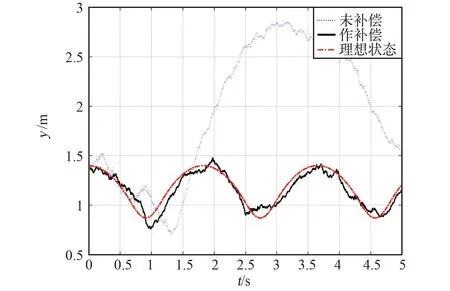
图10 被试人员y 方向位置Fig.10 Position of test subjects in the y direction

综合分析可知,在进行主动补偿后,被试人员的运动状态与真实失重的运动状态具有较好一致性,通过对误差因素的动态补偿,能够获得更逼真的微重力体验。

5 结论

本针对有限安装空间下速度和加速度测量传感器无法安装的问题,设计了三阶观测器实现对装置运动过程中速度及加速度的观测;在处理惯性力干扰和弹簧重力干扰时,采用非线性补偿方式使系统变为易于控制的线性定常系统。 本文所提的方法对采用弹簧装置的各类重力卸载机构的主动补偿均具有借鉴意义。

受电机响应速度、外部传感器精度等限制,当前的主动补偿系统还只能在限定条件下给出良好效果,下一步会对动力学参数的精确辨识、多传感器信息的融合使用等开展研究,有望进一步提升主动补偿的效果。