Asymmetrical spiral spectra and orbital angular momentum density of non-uniformly polarized vortex beams in uniaxial crystals

Ling-Yun Shu(舒凌云), Ke Cheng(程科), Sai Liao(廖赛),Meng-Ting Liang(梁梦婷), and Ceng-Hao Yang(杨嶒浩)

College of Optoelectronic Technology,Chengdu University of Information Technology,Chengdu 610225,China

Keywords: non-uniformly polarized beams,spiral spectrum,spin angular momentum,orbital angular momentum,vortex

1.Introduction

The influence of non-uniform polarization on angular momentums has inspired considerable enthusiasm in recent years.[1-5]Generally, angular momentum is comprised of orbital component related to helical wavefront of light beam and spin component associated with circular polarization.[6]The light beams with helical phases or vortex structures carry orbital angular momentum(OAM)per photon of±l¯hwith topological chargeland reduced-Planck constant ¯h.[7,8]Circularly polarized beams originating from the helical trace of the vectorial optical field possess an intrinsic spin angular momentum (SAM) of±¯h.[9,10]The spin-orbit interaction also plays an important role in producing novel optical phenomena such as microscopic, nano-optics, and surface plasmons fields.[11]The optical spin-orbit conversion can occur in the longitudinal component of the non-paraxial beam with non-uniform polarization.[12,13]

The decomposition of OAM or spiral spectrum is an important approach to dealing with OAM modes of complex optical fields.In isotropic media,a scalar beam presents symmetric power weight distribution of spiral spectra about a maximal weightm=l, and its longitudinal OAM density is also cylindrical symmetry or zero-value,and it is the sum of OAM density in the positivezdirection and that in the negativezdirection.[14,15]Asymmetric spiral spectra about the higher order Bessel-Gauss beams integrated in time (HOBBIT) system and the new Hermite-Gaussian(HG)vortex beam can be found in turbulence.[16,17]As typical anisotropic media, uniaxial crystals can show great flexibilities to design nonlinear optical elements.[18-20]It is natural to ask whether a vortex beam coupled with non-uniform polarization could show different properties of OAM in anisotropic media.Following our previous work,[21]we further explore the effect of nonuniform polarization on OAM (i.e., spiral spectra and OAM densities) in uniaxially anisotropic crystals.The results obtained in our work reveal that an asymmetry in power weight of spiral spectra and the non-zero value in the sum of longitudinal OAM densities originate from the initial non-uniform polarization at the input plane and anisotropy in uniaxial crystals,and the multi-lobes of SAM can induce the non-zero value of OAM even in non-vortex.The conclusions are beneficial to the OAM-based communication,optical metrology,and imaging by varying the initial non-uniform polarizations and vortex cores.[22-24]

2.Orbital angular momentum of NUPV beam in uniaxial crystal

Under the paraxial approximation, thex-andy-direction electric fields of the non-uniformly polarized vortex (NUPV)beams propagating in uniaxial crystals orthogonal to the optical axis in Cartesian coordinates obey the following equation:[25]

wherekis the wave number and the subscripts=xory,q=e orq=o.Ifs=x,thennq=ne(extraordinary refractive index),the signnq=no(i.e., ordinary refractive index) whens=y.Thexandycomponents of the input electric field ofEs(x,y,0)in Eq.(1)are expressed as[21,26,27]

whereθdenotes the angle between polarization and radial direction,δis the phase retardation angle between thexcomponent andycomponent,sgn(l)is the sign function,wandlare the waist width and topological charge of vortex core,respectively.Under the condition ofθ=0,δ=0 andθ=π/2,δ= 0, equation (2) reduces to the electric field of radially polarized vortex(RPV)beams and azimuthally polarized vortex (APV) beams, respectively.One can find that the NUPV beams can describe not only RPV and APV beams, but also a kind of hybridly polarized vortex(HPV)beams with linear,circular and elliptical polarization states in different spatial positions.

2.1.Spiral spectrum

To elucidate the spiral spectrum of thex-andy-direction electric field distributions, the complex field ofEs(x,y,z) can be projected into spiral harmonics eimφ.The expanded expression in a cylindrical coordinate system is written as[28,29]

whererandφare radial coordinate and azimuthal coordinate withx=rcosφandy=rsinφ,and the expansion coefficient is expressed as

The power weight of the spiral spectrum can be computed from

with the power of spiral spectrumPm.Equation (5) provides a powerful way to explore the relative energy of each spiral spectrum ofm-mode for the NUPV beams.Especially the spiral spectra of the input optical field with different polarization states are illustrated in Fig.1.From Figs.1(a1) and 1(a2), it is obvious that the spiral spectra of uniformly polarized vortex(UPV)beams centered atm=ldue to the embedded vortex cores with topological chargel,which indicates that these beams carry well-defined OAMs only at unique peak atm=l.However for NUPV beams their spiral spectra are concentrated atm=l±1 modes as shown in Figs.1(b1) and 1(d2),since the beam with non-vortex,i.e.,l=0, incredibly carries the same spiral spectra at ofm=-1 and +1 mode, respectively.One can find that the relation among topological chargel, mode of spiral spectramand the power weight valueRmcan be expressed asl=∑∞m=-∞mRmin such symmetric OAM spectra.[30]For example,for the case ofl=2 in Figs.1(b2)-1(d2), the power weights are 0.5 and 0.5 form= 1 and 3,respectively,and their weight values are both equal to 0.5 form=-1 and 1 withl=0 as shown in Figs.1(b1)-1(d1).These interesting phenomena demonstrate that spiral spectra of nonvortex optical fields can also be induced by non-uniform polarization in the initial field.The combined effect of non-uniform polarization and vortex structure leads to the concentration of spiral spectra atm=l±1 modes.

Next,our attention is focused onto the evolution of spiral spectra of NUPV beams and UPV beams in uniaxial crystals.When the beams travel through a uniaxial crystal along the direction orthogonal to the optical axis,they-component optical field follows the standard Fresnel diffraction in an isotropic medium with ordinary refractive index,the calculation results show that the weight values of spiral spectra ofy-direction optical field always remain the same value ofRm=l±1=0.5 in uniaxial crystal.Whereas thex-component optical field exhibits anisotropic diffraction,the evolution of spiral spectrum in an anisotropic medium is worth further studying.Unless otherwise specified, the abbreviation NUPV beam in the following refers to thexcomponent of the case ofθ=π/4 andδ=7π/8 in Eq.(1),and its polarization is a hybrid morphology with linear,right-handed and left-handed elliptical polarizations.Besides, the abbreviation UPV beam refers to thexcomponent of a uniformly polarized vortex beam with phase retardation ofδ=3π/8 in the following studies.The parameters are chosen to beλ=632.8 nm,w=1 mm,no=2.616(rutile crystals),and Rayleigh lengthze=kw2/2.

Figures 2(a1)-2(a4)and 2(b1)-2(b4)show the evolutions of spiral spectra of NUPV and UPV beams in uniaxial crystals for different topological chargelatne/no=1.5,respectively,and the weight curves of different spiral spectra inl=1 andl=-2 are also described in Figs.2(c1)-2(c4).One can find that spiral spectra concentrated atm=l±1 modes spread to other modes along with the positive and negative directions at an interval of Δm=2,which means that the power carried by initial spiral spectrum gradually disperses into those of other spiral spectra.In particular, the UPV beams still keeps symmetrical spiral spectra about a maximum weight value in uniaxial crystal, whereas for NUPV beams their distributions in spiral spectrum is asymmetrical.For example,the weight values ofm=-2, 0, 2, 4 modes in NUPV beams as shown inl=1 of Fig.2(a2) are 0.018, 0.57, 0.39, 0.025 respectively,while their weight values ofm=-1, 1, 3 in UPV beam(seel=1 of Fig.2(b2))equal 0.034,0.93,0.034,respectively.The UPV beams also exhibit another type of symmetry,which does not exist in NUPV beams.When|l| is the same, the weight value of the center position is the same, and the weight values on both sides of the center position are also symmetrically equal.Particularly in the case of NUPV beam as shown in weight curves in Figs.2(c1)and 2(c2),the two initial weights of 0.5 centered atm=l±1 modes present asynchronous behaviors.The weight of one mode starts to increase to a maximum value then it gradually decreases, but the other mode decreases to a lower weight.For the UPV beam the initial weight ofRm=1 decreases monotonically to a stable value,and the synchronous increase of the weights atm=-1 and 3,orm=-3 and 5 can be found atl=1 of Fig.2(c3).A similar case can be also found atl=-2 of UPV beam in Fig.2(c4).One can find that the equation ofl=∑∞m=-∞mRmstill holds true when the UPV beam propagates in a uniaxial anisotropic crystal, but for the NUPV beam the equation no longer holds true because of the embedded non-uniform polarization.More detailed data of the relationshipl=∑∞m=-∞mRmare given in Appendix A.It means that non-uniform polarization in the initial optical field can lead to the asymmetrical distribution of spiral spectrum propagating in uniaxial crystals, which provides a potential method for modulating the power carried by OAM modes.The asymmetric distribution results from joint action of the non-uniform polarization of the input plane and the anisotropy of the uniaxial crystal.The topological charge only affects the position and weight value of spiral mode.

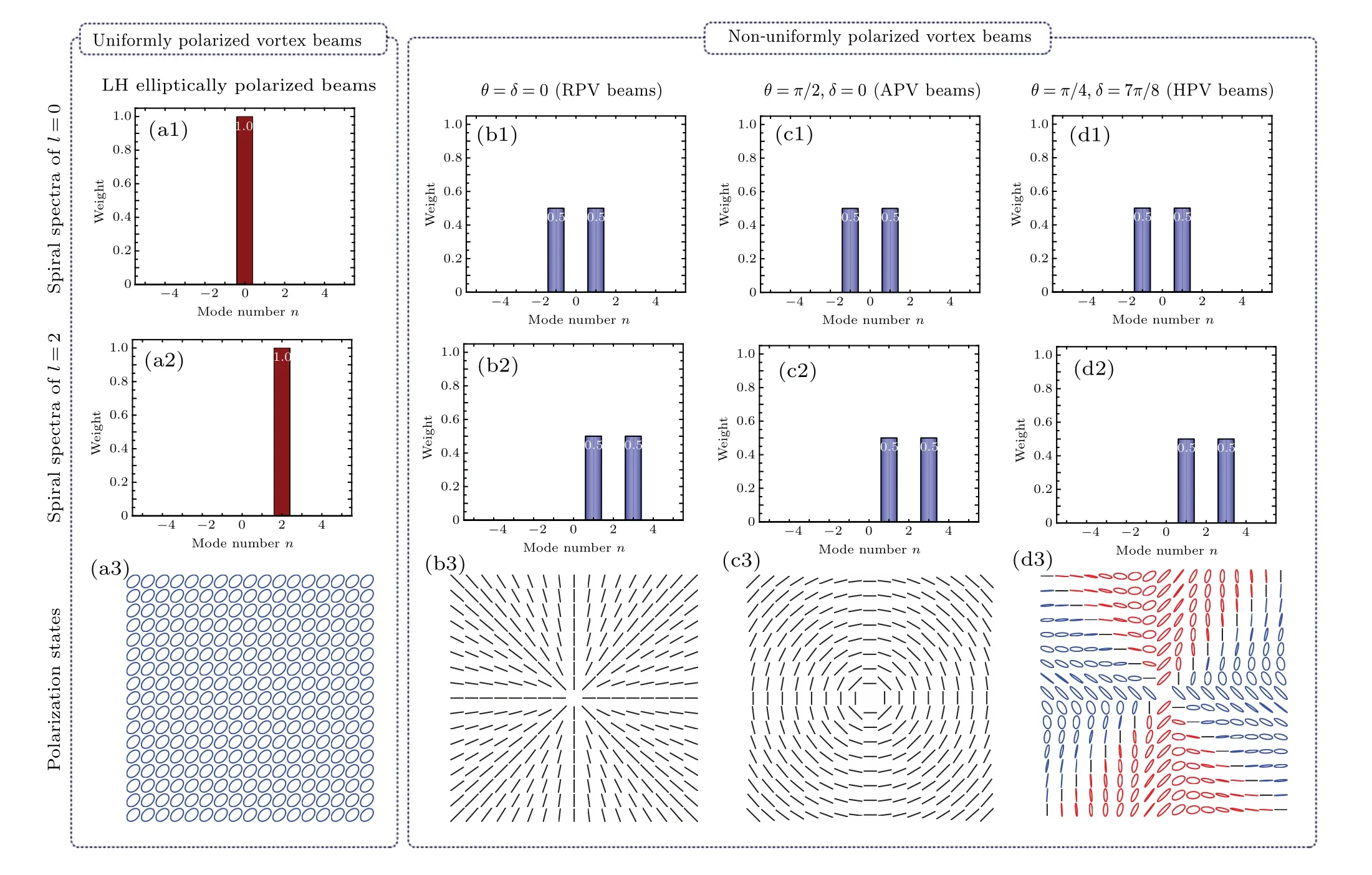
Fig.1.Spiral spectra of input optical field with different polarization states.Top row: spiral spectra of l=0;middle row: spiral spectra of l=2;bottom row:the right-handed polarization (red), left-handed elliptical polarization (blue), and linear polarization (black).(a1)-(a3) uniformly polarized vortex beams;(b1)-(b3)radially polarized vortex beams;(c1)-(c3)azimuthally polarized vortex beams;(d1)-(d3)hybridly polarized vortex beams.

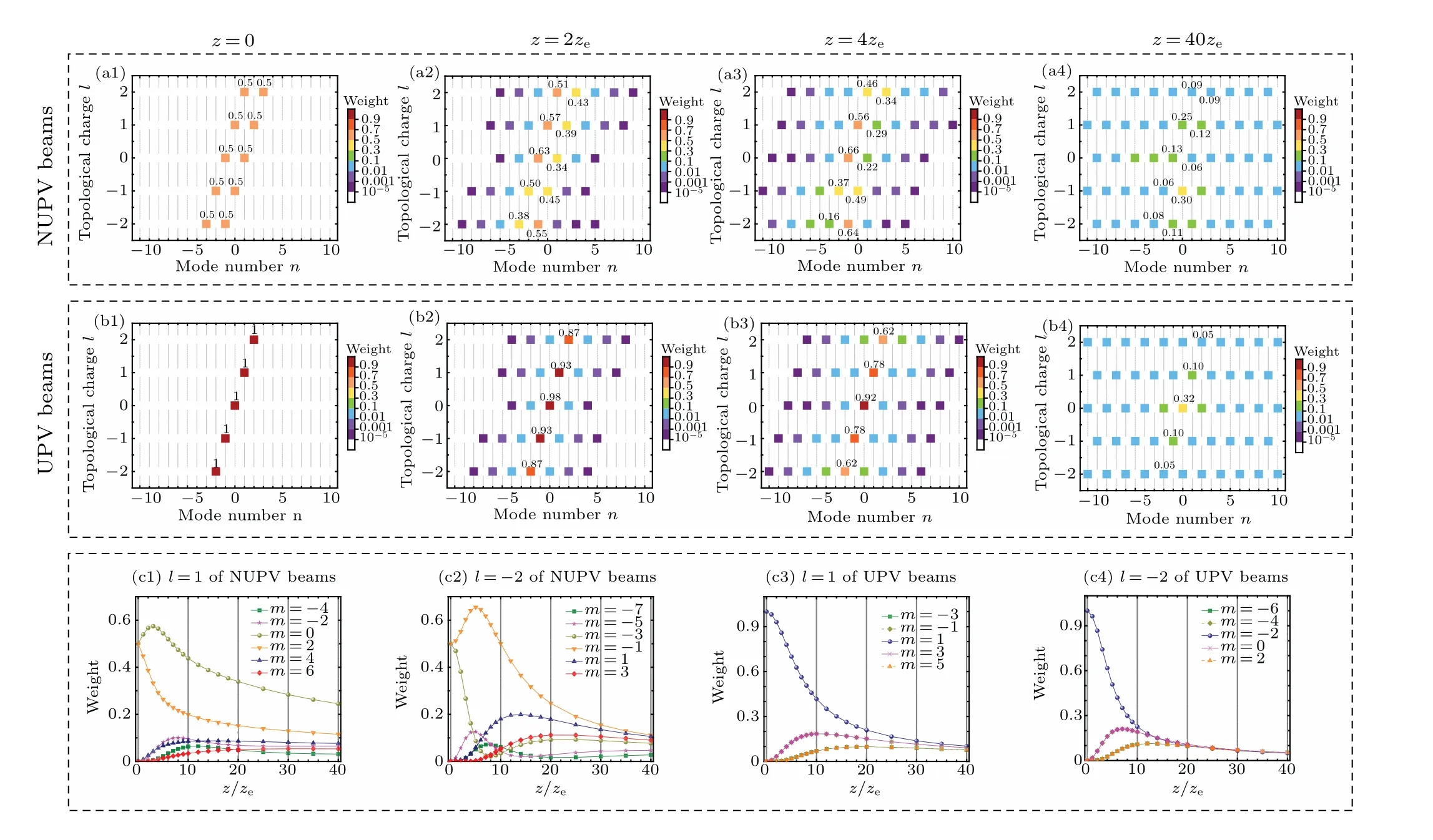
Fig.2.Evolutions of spiral spectra and weight values of NUPV and UPV beams in uniaxial crystals for different values of l with ne/no=1.5.(a1)-(a4)NUPV beams; (b1)-(b4)UPV beams;(c1)-(c2)weight curves of spiral spectra of NUPV beams with l=1 and l=-2;(c3)-(c4)weight curves of spiral spectra of UPV beams with l=1 and l=-2.

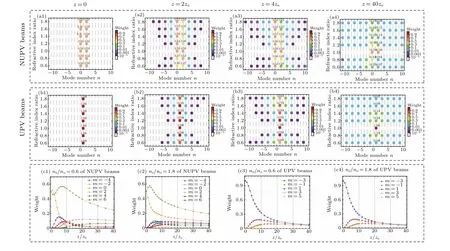
Fig.3.Evolutions of spiral spectra and weight values of NUPV and UPV beams in uniaxial crystals for different values of refractive index ratio ne/no with l=1.(a1)-(a4)NUPV beams;(b1)-(b4)UPV beams;(c1)-(c2)weight curves of spiral spectra of NUPV beams with ne/no=0.6 and ne/no=1.8;(c3)-(c4)weight curves of spiral spectra of UPV beams with ne/no=0.6 and ne/no=1.8.

The effect of refractive index ratione/noon spiral spectra of NUPV and UPV withl=1 beams in uniaxial crystals are plotted in Figs.3(a1)-3(a4)and 3(b1)-3(b4),respectively,and their weight curves in different modes atne/no=0.6 andne/no=1.8 are also given in Figs.3(c1)-3(c4).It is clearly seen that the weights of spiral spectra always remain the same forne/no=1, but the power at original modes can extend to other modes in anisotropic media forne/no/=1.More importantly, the extensions in weights of spiral spectra of UPV beams remain symmetrical in uniaxially anisotropic crystals for different values ofne/no, but the distributions of weight value at spiral spectra are asymmetrical for NUPV beams.In addition, the weight values atm=l=1 for UPV beams decrease monotonically, and the weights of other modes grow symmetrically with the increase of propagation distancez/zeas shown inne/no=0.6 andne/no=1.8 of Figs.3(c3)-3(c4).However for the NUPV beams the non-monotonic changes of weight at original modesm=l±1,e.g.,m=0 andm=2 in Figs.3(c1)-3(c2),also further verify the asymmetrical distributions of spiral spectra propagating in uniaxial crystals.The phenomenon means that the central mode with maximal weight in the NUPV beams can propagate in a lossless or highquality behavior, and the energy loss even in the far field is much smaller than that of the UPV beams.These results indicate that the asymmetrical spiral spectra in propagation originate from the joint action of input non-uniform polarization states at the initial plane and the anisotropy in uniaxial crystals.For the input field of the NUPV beams, even in the absence of vortex embedding,there are still weights on non-zero modes.The central modes of the NUPV beams have larger weight values than those of the UPV beams.Therefore, the information carried in the NUPV beams will be lost less than that in the UPV beams, which implies that the NUPV beams in OAM-based communication have higher degrees of freedom,capacities and robustness than UPV beams.

2.2.Vectorial orbital angular momentum density

It is well established that the light beams with helical wave-front structures can carry OAM of±l¯hper photon.[31]The OAM in vectorial structures satisfies the following relationship:

whereex,ey,andezare the unit vectors along the positivex,y,andzaxes,respectively.The components ofLx,Ly,andLzare given by[32,33]

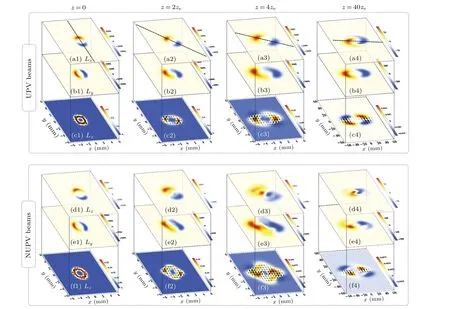
Fig.4.The x,y,and z components of the OAM densities of NUPV and UPV beams in uniaxial crystals with topological charge l=2 and ne/no=1.5,where the transverse OAM densities,i.e.,Lx and Ly,are also described by arrows.(a)and(d)Lx;(b)and(e)Ly;(c)and(f)Lz.

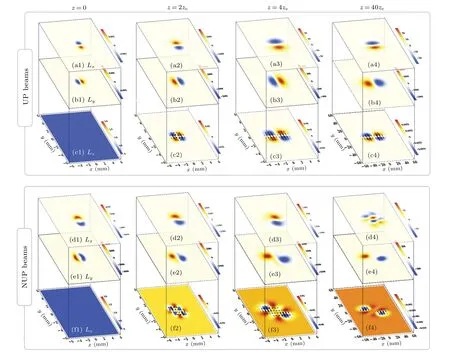
Fig.5.The x,y,and z components of the OAM densities of non-uniformly polarized(NUP)beams and UP beams with non-vortex in uniaxial crystals,where the transverse OAM densities,i.e.,Lx and Ly,are also described by arrows.The parameters are l=0 and ne/no=1.5.(a)and(d)Lx;(b)and(e)Ly;(c)and(f)Lz.

In an arbitrary polarization, theLzcomponent of light beam with non-vortex is generally equal to zero in free space or isotropic medium.[34]But the above analysis indicates that in uniaxially anisotropic crystals the spiral spectra of NUPV beams are asymmetrical due to non-uniform polarization at the input plane,our attention is paid to the effect of the embedded non-uniform polarization on the transversal and longitudinal OAM densities for non-vortex and vortex cases,respectively.

Numerical calculations taken from Eqs.(7)-(9) and shown in Figs.4 and 5 are used to explore the evolution of OAM in vectorial structures in a uniaxial crystal.It is clearly seen that the longitudinal OAM densities of the NUPV beams with topological chargel=2 become distorted from circular structures atz=0 to non-cylindrical patterns atz=40zein uniaxially anisotropic crystals as shown in Figs.4(f1)-4(f4).For the transversal OAM densities, the uniformity of the pattern is destroyed as the transmission distance increases.Thex-components of OAM densities,i.e.,Lx,display the rotation of two main-lobes anticlockwise.This can be seen intuitively from the rotation of the lobes in the transversal OAM density shown in Fig.4,where the center positions of two main-lobes are connected by a dashed lines.One can see that dashed lines are rotated by two lobes anticlockwise.However,such an obvious rotation phenomenon is not found inLy.Undoubtedly,the anisotropies in uniaxial crystals can lead to the distortion in OAM densities of NUPV and UPV beams due to faster spreading of light beams in thexdirection forne/no＆gt;1,and the sum ofLzof NUPV beams and the sum ofLzof UPV beams,in the presence of vortex and polarization,are both not equal to zero.However,from Figs.3(c4)and 3(f4),the sum ofLzof the UPV beams at the far field is closer to zero than that of the NUPV beams.What will happen if the vortex does not exist? For the case ofl=0, the OAM densities of both beams in the input plane satisfyLz=0 rather than circular structures as shown in Figs.5(c1)and 5(f1).From Figs.5(c1)-5(c4),one can find that the sum ofLzequals zero,with four stable lobes in longitudinal OAM densities forl=0.However,for non-uniformly polarized beams with non-vortex,the sum of the longitudinal OAM density,i.e.,Lz, is not equal to zero.These phenomena indicate that the non-zero appearance of the sums ofLzin the NUPV beam is caused by a joint effect of the input nonuniform polarization and anisotropy.

Figure 6 further gives thezcomponents of SAM and OAM densities of uniformly polarized (UP) and NUP beams with non-vortex in uniaxial crystals.Their OAM densities can be found for UP and NUP beams as shown in Figs.6(b2)and 6(d2).The fact ofLz=0 for UP beams even in anisotropic media indicates that the anisotropy in uniaxial crystal cannot change orbital angular momentum.Whereas for NUP beams theLz/=0 in anisotropic medium means that the input non-uniform polarization, or the input multi-lobes SAM in Fig.6(c1) can induce non-zero value inLz.Therefore, the non-zero value inLzis not caused by anisotropy, but by the input non-uniform polarization or the input multi-lobe SAM.

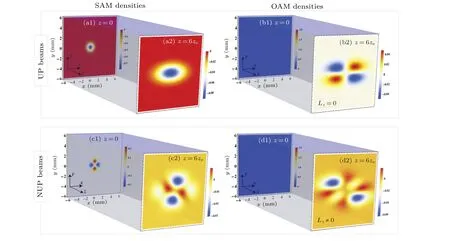
Fig.6.The z components of SAM and OAM densities of UP and NUP beams with non-vortex in uniaxial crystals at different propagation distances.The parameters are l=0 and ne/no=1.5.(a)and(c)SAM densities;(b)and(d)OAM densities.

2.3.Relation between spiral spectrum and longitudinal OAM density

The above analysis indicates that a non-uniform polarization can result in the asymmetrical distributions of spiral spectra and a non-zero value in the sum ofLz.The spiral spectra and longitudinal OAM densities provide different perspectives for exploring the evolution of OAM,and their relations are determined by[28,35]

Figure 7 displays the ratio of positive part and negative part to the total OAM of NUPV and UPV beams in uniaxial crystals for different values of refractive index ratione/no=0.6,1,1.8,andl=1,respectively.From Figs.7(a1)and 7(b1),it can be found that the values ofR-σin spiral spectra and longitudinal OAM densities both monotonically increase, and the values ofR+σdecrease in two different ways as shown in Figs.7(a2) and 7(b2).When the NUPV beams propagate in uniaxial crystals, the increase the values ofR-σmeans that the weight of negative OAM gradually grows from zero-value, while the values of the positive part,i.e.,R+σ, decrease from maximal values.Compared with UPV beams,the NUPV beams present a greater range of change inR+σandR-σ.The results confirm that the asymmetrical distribution of spiral spectra as shown in Figs.3(a1)-3(a4) in NUPV beams.The change ofR+σandR-σbecome increasingly intense with the augment of the difference between refractive index ratione/noand 1,while forne/no=1 the values ofR+σandR-σremain unchanged, which indicates that the anisotropy can further strengthen the asymmetrical distribution of spiral spectra and a non-zero value in the sum ofLzinduced by non-uniform polarization.

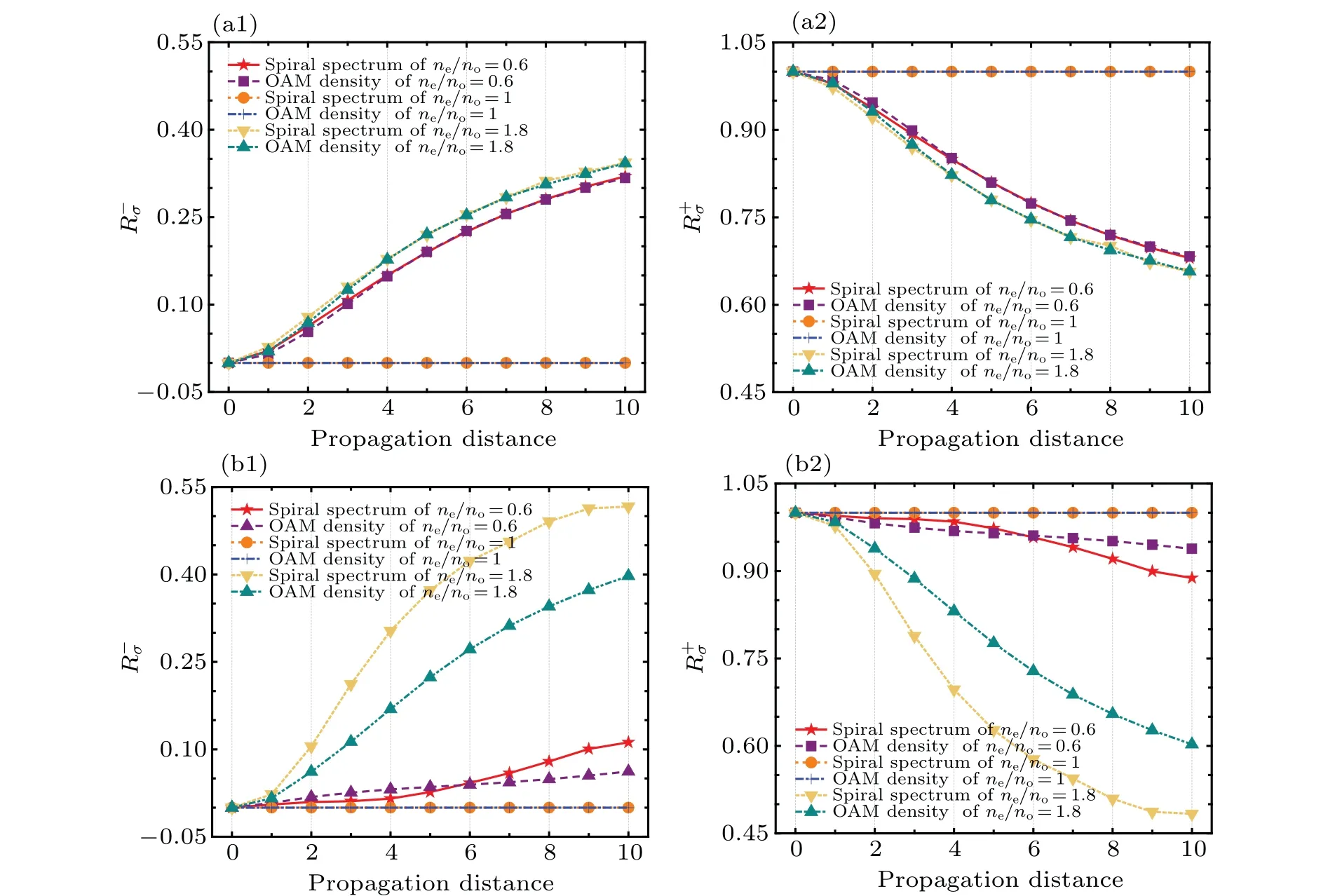
Fig.7.Ratios of positive part R+σ and negative part R-σ to the total OAM of NUPV and UPV beams in uniaxial crystals for different refractive index ratios ne/no=0.6,1,1.8,and l=1,respectively.(a1)and(a2)UPV beams;(b1)and(b2)NUPV beams.

3.Conclusions

Based on the beam model in our previous work, the spiral spectra and OAM densities of NUPV and UPV beams in uniaxial crystals are further studied.For the NUPV beams,their positions of modesmconcentrated atm=l±1 rather thanm=lin spiral spectra,and the relation among topological chargel, mode of spiral spectramand the power weight valueRmcan be expressed asl= ∑∞m=-∞mRmat the input plane.In the uniaxially anisotropic crystals the relation ofl=∑∞m=-∞mRmstill holds true for UPV beams, whereas for NUPV beams their relations are no longer valid due to the nonuniform polarization.

The influence of non-uniform polarization, topological charge and refractive index ratio on spiral spectra and OAM densities of NUPV and UPV beams are also explored by anisotropic diffraction in thex-component electric field.The UPV beams possess symmetrical power weights of spiral spectra even in anisotropic media, whereas the symmetrical distribution in power weights of spiral spectra disappears for the NUPV beams.The results show that the asymmetrical spiral spectra originate from the joint action of the input nonuniform polarization and anisotropy in uniaxial crystals.The topological charge affects the position and weight value of modes.Furthermore,the sum of the longitudinal OAM densitiesLzfor NUPV beams with non-vortex is not equal to zero,which are different from that of the UPV beams.It indicates that the non-zero value inLzis related to the anisotropy and the input non-uniform polarization.The anisotropy in uniaxial crystals results in the extension of the spiral spectrum and the distortion ofLz.Based on such effects, the asymmetric spiral spectra and the non-zero values of the sums ofLzare obtained under the joint effect of anisotropy and input nonuniform polarization.These interesting phenomena may be explained by the conversion of optical SAM related to nonuniform polarization into OAM.[36]The relation between spiral spectrum and longitudinal OAM density is also discussed.The consistency of two different methods,i.e., spiral spectra and OAM densities,in exploring OAM are numerically elucidated by the definedR±σ.The NUPV beams present a greater range of change inR±σthan the UPV beams.The OAM change induced by the initial non-uniform polarization has potential applications in OAM-based communications, optical metrology and imaging.

Appendix A: Sums ofmRmof NUPV and UPV beams

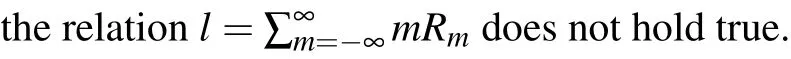
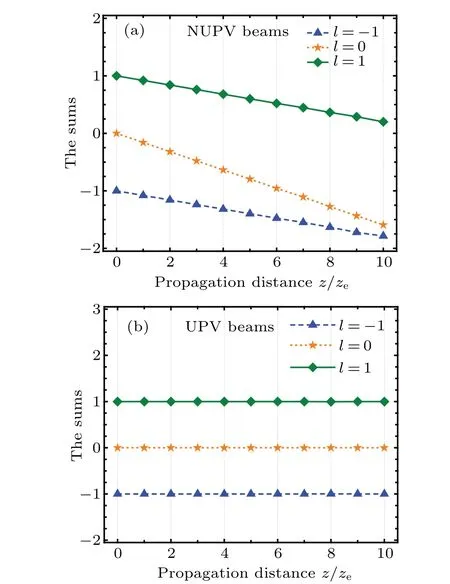
Fig.A1.Sums of mRm of NUPV and UPV beams in uniaxial crystals with ne/no=1.5 and different values of vortex topological charge l.(a)NUPV beams;(b)UPV beams.

Acknowledgement

Project supported by the Science and Technology Program of Sichuan Province,China(Grant No.23NSFSC1097).