Spontaneous emission of a moving atom in a waveguide of rectangular cross section

Jing Zeng(曾静), Jing Lu(卢竞), and Lan Zhou(周兰)

Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education,Department of Physics

and Synergetic Innovation Center of Quantum Effects and Applications,Hunan Normal University,Changsha 410081,China

Keywords: spontaneous emission,moving atom,waveguide of rectangular cross section

1.Introduction

Photons are desirable for distributing information and transferring entanglement in quantum networks.With the demanding to build a device in a quantum network for controlling single photon, single quantum emitter (hereafter, we will often use the word “atom” instead of “quantum emitter”) would be desirable since there are no direct interaction among photons.A nonrelativistic two-level system(TLS)acts as a quantum switch in a one-dimensional (1D) waveguide with linear dispersion relation[1-3]or a 1D coupled-resonator waveguide(CRW).[4]A V-type or ladder-type atom functions as the frequency converter for single photon[5]in a 1D waveguide.A cyclic or a Λ-type atom works as a multichannel quantum router,[6-8]proposed to act as quantum nodes in extended communication networks and scalable computational devices.[9-29]Photons propagating along the network are confined in a 1D waveguide.With the mode volume decreased,the coupling strength of atom to the waveguide is enhanced.The atomic spontaneous emission (SE) has played an important role on controlling photon transport in quantum network.

One of the studies in waveguide quantum electrodynamics (QED) is how to use atoms to control the transmission of photons.SE of atoms have been found to play an important role, but the existing researches basically have assumed that the center of mass of atoms is fixed.Theoretically speaking,the kinetic energy of an atom being stationary is completely uncertain, requiring an additional great amount of energy to bring the atom to be stationary.From an experimental point of view,since the system cannot be at absolute zero temperature,it is objective that the kinetic energy of atoms is nonzero.SE is a result of the electromagnetic interaction between an atom and a quantum field.It is a process as follows: a system initially in an excited state relaxed to its lower state and emitting a quanta of energy to its surrounding vacuum field,which carries away the difference in energy between the two levels.Different from atoms in a cavity or a free space,atoms used to control single photon in quantum networks interact with their surrounding electromagnetic (EM) field which is confined in a 1D waveguide.SE has been widely studied in free space,e.g., in a semi-infinite or infinite 1D waveguide.However,most works focus on 1D waveguide without a cross section,and the atom under study is usually assumed to be stationary.A stationary atom possesses an undetermined kinetic energy according to the Heisenberg’s uncertainty relation.Thus, the stationary-atom model is too simple.In this paper, we study the spontaneous radiative decay of an atom moving in an infinite waveguide of rectangular cross section.We analyze the interaction of an initially excited TLS with the waveguide in vacuum.When an initially excited TLS spontaneously emits a photon into the waveguide, the atomic center of mass (c.m.)experiences a change in momentum space.The dynamical behavior of the TLS is studied by taking the quantization of TLS’s momentum and position into account.

This paper is organized as follows.In Section 2, we introduce the model and establish the notation.In Section 3,we derive the relevant equations describing the dynamics of the system for the case of the TLS being initially excited and the waveguide modes in the vacuum state.In Section 4,the spontaneous emission rate has been presented for TLS initially at rest and moving respectively.We make a conclusion in Section 5.

2.Model setup

The system we studied is shown in Fig.1.A waveguide made of ideal perfect conducting walls is formed from surfaces atx=0,x=a,y=0,y=b, and is placed along thezaxis.

Fig.1.Schematic illustration for the two-level atom inside a infinite waveguide of rectangular cross section.

We have set ¯h=1.We consider the atomic electric dipole is oriented along thezdirection,which means that the TLS only interacts with the TMmnmodes.Since the number (m,n,k)specifies the mode function of this air-filled metal pipe waveguide, we label the annihilation operator for each TM guiding mode byamnk.The free Hamiltonian for the waveguide is described by

There are two types of modes for the field in the waveguide: TE modes whose electric field has no longitudinal component, and TM modes whose magnetic field has no longitudinal component.Letk=(kx,ky,k)be the wave vector.The relationskx=mπ/aandky=nπ/awith positive integersn,mcan be imposed by the condition that the tangential components of the electric field vanish at all the conducting wall,however,there is no constraint onk.Therefore,the waveguide allows a continuous range of frequencies described by the dispersion relation

A TLS with massMand the transition frequencyωAis inside the waveguide.It has two internal states: the upper level|e〉and the lower level|g〉,which introduce the the rising(lowering)atomic operator ˆσ+≡|e〉〈g|(ˆσ-≡|g〉〈e|).We assume that the atom moves only along thezaxis,which means that the atom has unchanged position along thexyplane.The atomic momentum and position are characterized by the operators ˆpzand ˆr=(x0,y0,ˆz), respectively, wherex0andy0are constant.The momentum and position of the atomic center of mass obey canonical commutation relations.The free Hamiltonian for the TLS is described by

Here,ε0represents the permittivity of free space,dthe magnitude of the transition dipole moment of the TLS and assumed to be real,A=abthe area of the rectangular cross section.

The TLS located atx0=a/2 andy0=b/2 decouples to the TMmnguiding mode with even integermorn.The total system is described by HamiltonianH=Ha+Hf+HI.

3.Dynamic of the moving atom

Let us introduce the operators of the excited number and the atom-field momentum as follows:

It can be found that bothNeandNpare commuted with the total HamiltonianHof the system.Thus,the excited number and atom-field momentum are conservative quantities.It is well-known that a stationary TLS being excited initially will evolve into a superposition of initial state itself and the state in which the TLS is unexcited and has released a photon into the field.However, when the quantization of the atomic momentum and position are taken into account,the conservation of momentum indicates that the c.m.motion of the atom is changed by the recoil caused by the emission of photons.

The initial wave function of the system we considered is in a product state|ψ(0)〉=|e,pz,0〉, where|pz〉is an eigenstate of the momentum operator ˆpzcorresponding to the eigenvaluepzand the field is in the vacuum state.The time evolution of the state|ψt〉is described by the Schr¨odinger equation.Via the Fourier transformation, the Green operator ˆG=(q- ˆH)-1relates the state|ψt〉to the initial state|ψ0〉,which yields

The probability of finding the atom in its excited state equals the probability for finding the TLS in its initial state|ψ0〉,which is denoted byPA=|〈ψ0|ψt〉|2.Since the atom-field coupling energyHIis small compared with the free energyH0=Hs+Hf, the Green operator ˆGcan be expanded into a series of ascending powers ofHI.By defining the free Green operator ˆG0=(q- ˆH0)-1,the probabilityPAcan be rewritten as

Equation (10) can be solved by the residue theorem, but the solution of the equation

must be found.Since Eq.(12) is a transcendental equation involving integral,the approximations are used to give an analytic discussion.In this following discussion,for the sake of simplification,we denote the transversally confined propagating modes which couple to the atom as TMjwithj=(m,n)according to the ascending order of the cutoff frequencies.

4.Spontaneous emission

The roots of the denominator in Eq.(11)can be split into a sum of the singular and principal value parts.The principal part is merely included into redefinition of the energy.The singular part gives the decay rate due to the coupling to field.If the coupling strengthgmnkis small,the solution of Eq.(12)can be expanded into a series of ascending powers ofgjk.Under the second-order approximation about the weak coupling,the atomic decay is dominantly exponential with rate

The delta function expresses the conservation of energy before and after the emission.We express the integral in Eq.(13)in terms of the frequency

by using the dispersion relation,where the coupling strength

4.1.The TLS being initially at rest

We now assume that the TLS is initially at rest, i.e.,pz=0.The spontaneous decay rate becomes

It can be found that the modal profile affects on the decay rate via location of the TLS.If the atom is located atx0=a/2 andy0=b/2, no photons are radiated into the TMmnguiding modes with even integermornsince the guiding modes are standing waves in the transverse direction.As the initial atomic energyωAapproaches one of the cutoff frequencies,the TLS loses its energy very quickly.The more transverse modes interact with the TLS,the faster the TLS decays.The massMalso contributes to the spontaneous emission rate due to the recoil of the TLS.

To compare with the TLS fixed inside a waveguide with a rectangular cross section,we consider the mass is larger and keep the first order ofM-1.Then the spontaneous rate reduces to

which is smaller than the spontaneous rateΓf≡∑j ΓSjof the TLS fixed in the vacuum of the waveguide with a rectangular cross section.Here,

is the decay rate of a stationary TLS due to its interacting with the vacuum of the TMmntransverse mode.The frequency of the emitted photon approximately reads

It shows that the cutoff frequencies around the transition frequencyωAdetermines thatωRis smaller than the transition frequency of the TLS.If the mass of the TLS is so large that the recoil can be neglect,we recover the decay rate of the stationary TLS and the frequencyωAof the emitted photon.

4.2.The TLS initially moving

When the atom is not initially at rest,i.e.,pz/=0,the roots of the following equations

determine the frequency of the emitted photon as well as the value of spontaneous rate.We note the Hamiltonian is written in the nonrelativistic region where the c.m.motion of the TLS is very slower than light, so we apply the perturbation approach to Eq.(22)to find the analytic solutions,

Here,λis a continuously varying parameter ranging from zero to unity;ω0is of the zeroth order in(Mc)-1,ω1is of the first order in(Mc)-1.We now substitute Eq.(23)into Eq.(22)and retain only terms up to the first order in(Mc)-1.We approximately obtain frequencies of the emitted photon as follows:

The nonvanishing initial c.m.motion of the TLS splits the frequency of the emitted photon in Eq.(21) into two.For the emitted photon traveling along the same direction of the initial TLS momentum, its carried frequency is decreased.For the emitted photon traveling in the opposite direction of the initial TLS momentum,its carried frequency is increased.The emission of the right-going and left-going photon along thezaxis leads to a loss of TLS’s energy with rate

For a moving atom,the massM,the initial momentumpzand the cutoff frequenciesΩjall contribute to the decay rate.Asω±approaches one of the cutoff frequencies,the TLS loses its energy very quickly.The more transverse modes interact with the TLS, the faster the TLS decays.For a much larger mass,the decay rate reads

in the second order ofM-1.Here, the contribution of the momentumpzis related to the second order ofM-1.Obviously,ΓMcan be well simplified to the special case where the initial momentum of the TLSpz=0, as we have shown in Eq.(19).Compared Eq.(19)with Eq.(26), it is obvious that the first order ofM-1is only related to the recoil of atomic mass.As a result of the nonzero initial momentumpz, the atomic SE rateΓMis further reduced.In order to discuss the effect of cutoff frequencyΩjon the atomic SE rate, we have plotted the (ΓM-ΓR)/ΓRas a function of the dimensionless difference(ω2A-Ω211)/Ω211in Fig.2.It can be observed that when the atomic transition frequencyωAapproaches the lowest cutoff frequencyΩ11,the|ΓM-ΓR|(the influence of atomic nonzero initial momentumpzon atomic SE rate)increases significantly.This shows that the effect of thepzon the atomic radiation is not negligible whenωA→Ωj, even in the nonrelativistic region.

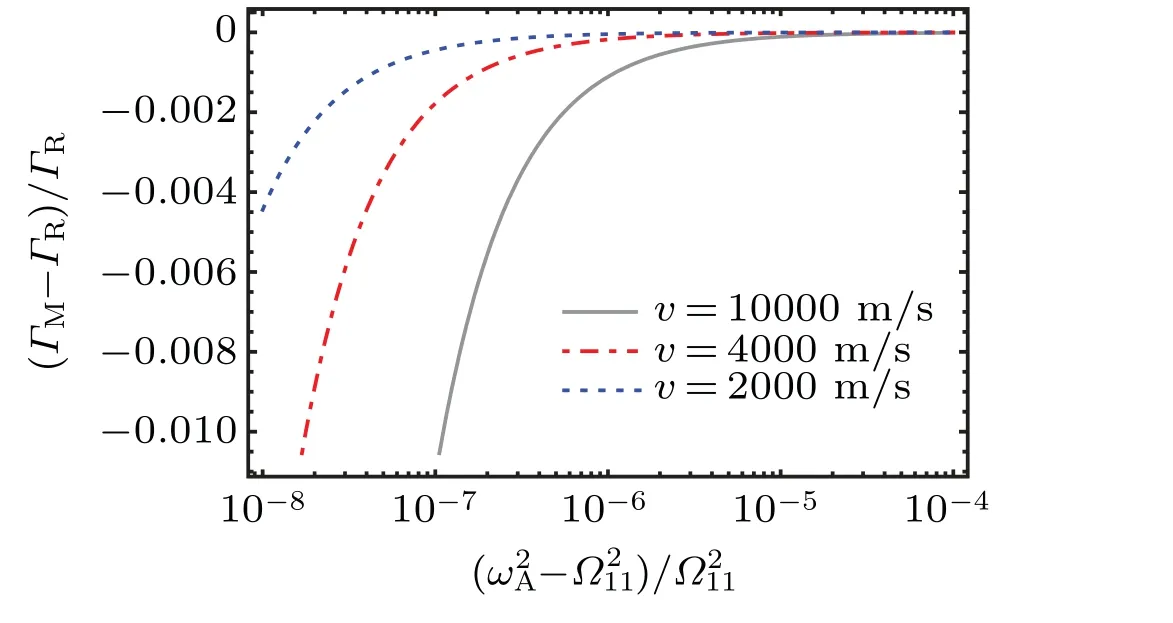
Fig.2.(ΓM-ΓR)/ΓR as a function of the dimensionless difference(ω2A-Ω211)/Ω211 for different initial atomic velocities: v=10000 m/s(grey solid line), v = 4000 m/s (red dot-dashed line), v = 2000 m/s(blue dotted line).We have set the following parameters: ¯hΩ11/Mc2=1×10-40/π.

It is worthwhile to note that the eigenfrequencyωjkof the radiation field mode in the waveguide has a nonlinear relationship with the wave vector, as shown in Eq.(1).Each transverse mode has a cutoff frequency, and there is a nonzero lower limit for the eigenfrequency of radiation,unlike the radiation field mode in free space.In a single transverse mode of the waveguide,the spontaneous radiation of a moving atom decreases with the increase of atomic transition frequencyωA,which is exactly opposite to the radiation of moving atoms in free space.However, the SE rate increases significantly as shown in Eq.(20), when the atomic transition frequency is close to the cutoff frequency of other transverse modes.

5.Conclusion

We consider a TLS interacting with a waveguide of rectangular cross section.The spontaneous emission of an atom in vacuum is studied.Both atom and field variables are fully quantized, so that the atomic recoil on the emission of radiation are automatically included in the calculation.Under the second order approximation of the weak coupling,the SE rate and the frequency of the emitted photon for the atom initial being at rest or moving are obtained.It is shown that the modal profile affects on the decay rate via location of the TLS, the more transverse modes interact with the TLS, the faster the TLS decays.For the TLS initially being at rest,the transition frequencyωAof the TLS determines the speed of the SE rate.AsωAapproaches any of the cutoff frequencies, the TLS decays fast.In the first order of SE, the SE rate is smaller than the SE rate of the TLS fixed in the vacuum of the same waveguide,and the frequency of the emitted photon could be smaller than the initial energyωAof the total system.For the TLS initially being moving, the carried frequency of the emitted photon is decreased when it travels along the direction of the initial momentum of the TLS and is increased when it travels in the opposite direction of the initial momentum of the TLS.The SE rate is smaller than the SE rate of the TLS fixed in the vacuum of the same waveguide but it is dependent on the initial momentum in the second order of SE.

Acknowledgements

Project supported by the Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province, China (Grant No.2020RC4047), and the National Natural Science Foundation of China (Grant Nos.11975095,12075082,and 11935006).