用无穷矩阵方程求解第二类Stirling数表示的自然数幂和
唐军强,艾英
用无穷矩阵方程求解第二类Stirling数表示的自然数幂和
唐军强,艾英
(焦作大学 基础部,河南 焦作 454000)
讨论了4个用第二类Stirling数表示的自然数的幂和公式.利用升阶乘和降阶乘的定义式,得到关于各阶幂和的递推关系,用求解无穷矩阵方程的方法给出用第二类Stirling数表示的幂和公式,并证明了它们之间的等价性.
无穷矩阵方程;自然数;幂和;第一类Stirling数;第二类Stirling数
1 引言及预备知识
自然数的幂和是一个古老的问题,很多数学家都对其做过研究.该问题牵涉极广,可以用Bernoulli数、第二类Stirling数、第二类Euler数等给出它的计算公式[1-2].仅用第二类Stirling数就可以给出4个形式上看起来不同的公式,这容易使人感到困惑.本文基于构造无穷矩阵方程的方法,给出这些公式的推导过程,并讨论它们之间的等价性.
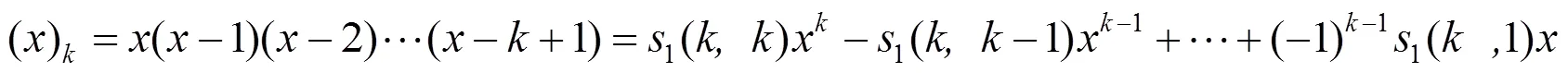

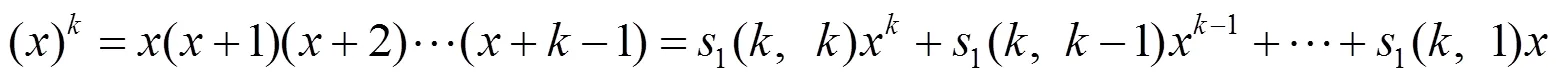
它的逆过程是

第二类Stirling数满足运算规则
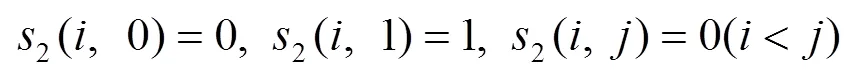
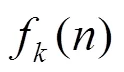
证明 将各式
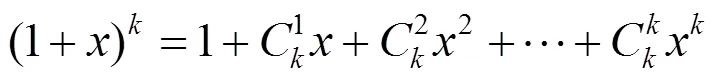
…

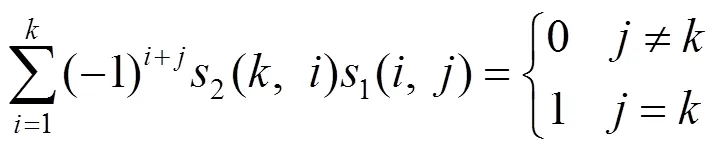
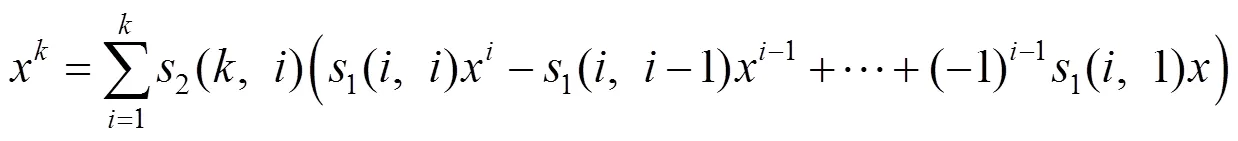
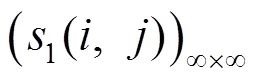
2 用第二类Stirling数表示的幂和公式
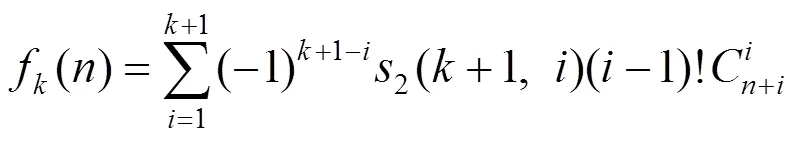
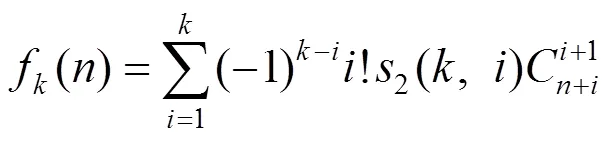
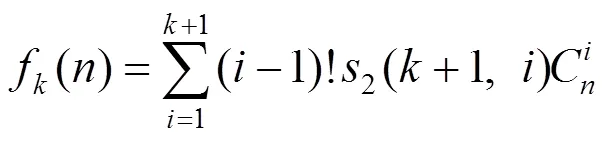
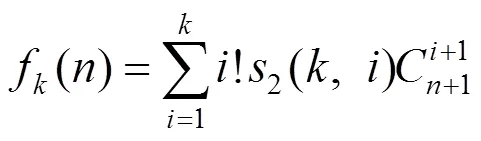
证明推导式(7),采用第一类Stirling数的升阶乘定义式
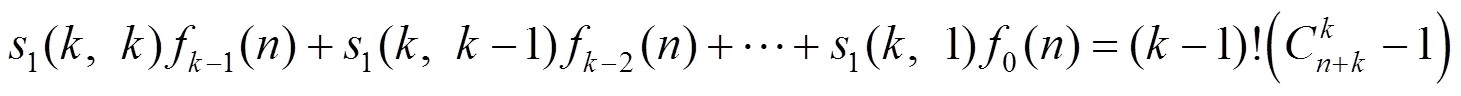
式(8)可以由式(7)推导得出,利用式(5),得到
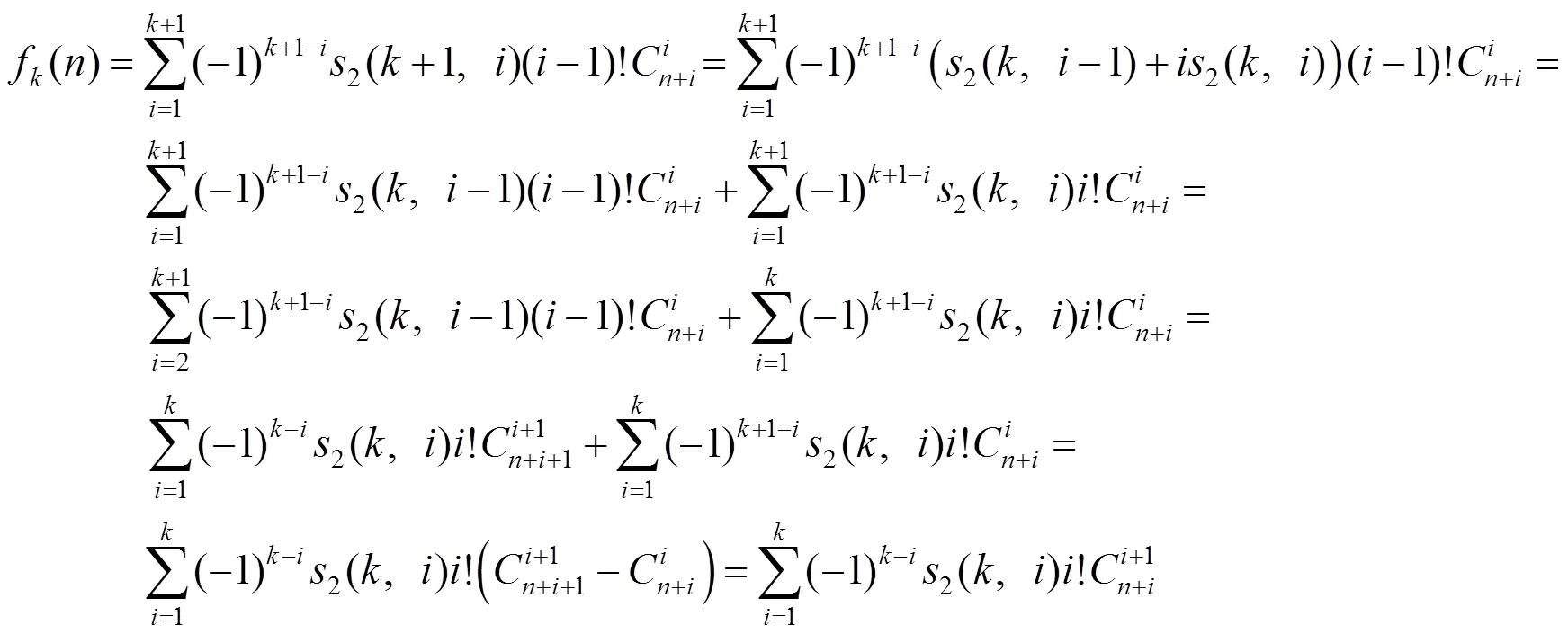

注式(8)(10)较常见于文献[6-9]中,式(7)(9)是本文的结果,且由式(7)可以推得式(8),由式(9)可以推得式(10).
3 结语
本文的方法具有普遍性.递推关系通常是一种线性关系,而其复杂的计算过程往往使人望而生畏,从矩阵方程的角度看待一些递推关系式,通常会收获意想不到的效果.由于矩阵具有全局性,递推关系所满足的线性特征都包含于矩阵当中,因此可以通过求无穷矩阵的逆,从其逆矩阵的元素中发现规律性,进而获得所求对象的一种通用表达式.对于用Berboulli数形式表示的幂和公式,也可以进行类似的操作,只是所用的递推关系式不同[10].至于从逆矩阵中发现规律性,则是一个计算、类比和归纳的过程,同时要对各类常用的数学常数有敏感的认知.
[1] 罗见今.李善兰对Stirling数和Euler数的研究[J].数学研究与评论,1982,2(4):173-182.
[2] 罗见今.自然数幂和公式的发展[J].高等数学研究,2004,7(4):56-61.
[3] 王竹溪,郭敦仁.特殊函数论[M].北京:科学出版社,1965:1-15.

[5] 莫里斯·克莱因(美).古今数学思想:二[M].北京大学数学系数学史翻译组,译.上海:上海科学技术出版社,1979:178-180.
[6] 邓艳平,王云葵.等幂和与Stirling数的奇妙关系[J].广西师范学院学报,1998,15(4):316-317.
[7] 尹志凌,张升,陈宝平.Stirling数表示自然数方幂和[J].内蒙古农业大学学报,2010,31(1):267-270.
[8] 王红,杨雅琴,王艳辉.第一类Stirling数和第二类Stirling数的关系式[J].高师理科学刊,2008,28(6):37-39.
[9] 褚维盘,党四善.联系Bernoulli数和第二类Stirling数的一个恒等式[J].纯粹数学与应用数学,2004,20(3):282-284.
[10] 杨胜良,乔占科.计算幂和多项式的矩阵方法[J].数学的实践与认识,2008,38(3):90-95.
Power sum of natural numbers expressed by Stirling numbers of second kind by solving infinite matrix equation
TANG Junqiang,AI Ying
(Department of Basic Courses,Jiaozuo College,Jiaozuo 454000,China )
Four power sum formulas of natural numbers expressed by Stirling numbers of second kind are discussed.By means of the definition of rising factorial and falling factorial,the recursive relation of the power sum of each order is obtained,and the formula of the power sum expressed by the Stirling numbers of second kind is given by means of solving the infinite matrix equation,and the equivalence between them is proved.
infinite matrix equation;natural number;power sum;Stirling numbers of first kind;Stirling numbers of second kind
1007-9831(2023)01-0020-04
O156
A
10.3969/j.issn.1007-9831.2023.01.005
2022-05-28
河南省自然科学基金项目(222300420579)
唐军强(1980-),男,河南开封人,讲师,硕士,从事解析数论研究.E-mail:tjq_1999@sina.com

