后疫情时代应急物资调度排队模型优化研究

刘俊杰，孙钦莹（黑龙江大学 信息管理学院，黑龙江 哈尔滨 150006）

0 引言

重大突发公共卫生事件有突发性、衍生性、广泛影响性、不确定性、社会危害大等特点，给人民群众的身体健康和生命安全带来严重损害[1]。应急物流不同于一般的物流，是在重大突发事件发生时运输应急救援物资而提出的特殊概念，应急物流追求时间效益的最大化和突发事件损失的最小化，旨在提高应急救援效率[2]。同时，应急物资调度是应急物资保障机制的基础环节，直接影响着应急救援的响应速度和效果[3]。因此，如何提高应急物资救援的效率？如何保持物流中转站的服务系统高效工作？这是应急管理人员亟待解决的问题，只有在应急物资调度时节省物流中转站的服务时间，才能提高物资转运效率，提高新冠肺炎疫情期间应急救援效率，实现时间效益最大化和灾害损失最小化。

本文以武汉市宝湾物流园为实例，建立排队论M/M/1 模型和M/M/C 模型，并且列出应急物资运载车辆的平均等待时间及平均等待队长公式，搜索相关数据计算并比较运行指标，得出通过提高服务强度、增设服务台数量等方式，缩短物资的调度时间，提高应急救援的效率，减少人民在灾难中的损失，达到时间效益最大化和损失最小化的目标，这也为其他突发事件发生时合理安排救援物资运输决策问题提供参考依据。

1 研究现状

排队论（随机服务系统理论）是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法，可以对存在排队现象的离散事件系统进行有效分析[4]。

通过大量文献调研，国外将排队论方法运用在应急领域的研究如下，Wiler J L[5]推导和验证了一种新的基于排队理论的模型，该模型可预测各种患者拥挤场景对患者离开而不被看到（LWBS）率的影响。Xie J[6]开发了一个包含转移和放弃的排队模型来研究医疗保健系统。Joseph J W[7]提出基于排队理论的排队方程模拟急诊科（ED）内不同流程的需求，并有助于考虑可变性对延迟和服务时间的影响。Du L[8]建立基于排队论的人工智能的大规模突发事件中的医疗应急资源分配模型，有助于缩短应急物资准备、调度和运输的总时间。由文献分析可知，近些年国外对于排队论较多应用于医疗应急领域，但较少应用于应急物资调度方面。

国内学者近些年将排队论方法广泛应用于应急管理领域[9-14]，庞剑飞等人[15]运用排队论和Stateflow 设计应急医疗救援仿真系统，模拟了应急医疗救援的实际过程，证明系统有可行性和有效性。乔联宝等人[16]建立β 可靠性最大的覆盖应急服务车辆选址的排队论模型，并设计了效果优良的求解算法。在应急物资调度方面，李聪等人[17]运用排队论方法，建立了GI/M/1 应急物资排队论模型，推导应急运载车辆的平均等待时间和平均等待队长公式，用Extendsim 软件进行了仿真检验，同年，提出有优先权的M/M/1 模型，运用SimEvents 软件对其仿真，为决策者是否增减运输车辆和物资服务台数量提供了依据和参考。杜亚涵等人[18]运用排队论方法，建立应急物资的供应链排队模型，计算应急物资供应链响应的最短时间，保障应急物资的紧急供应。

综上文献调研情况，国内外将排队论方法的应用领域非常广泛，但应用于应急物资调度和转运的研究却较少。由于突发事件灾害不可避免，应急物资转运问题是政府及人民一直关注的重点。因此，本文根据新冠疫情期间应急物资车辆调度实际情况，建立排队论M/M/1 模型和M/M/C 模型，得出应急物资运载车辆的平均等待时间及平均等待队长，并将模型优化前后的运行指标结果进行对比，可以为实际突发事件发生时提高救援物资调度效率提供优化方案。

2 应急物资调度排队论模型构建

2.1 模型可应用性

在疫情期间，需要大量车辆运载救援物资如口罩、防护服、消毒酒精、测温仪、食物等运送至武汉物流园再调度转运至其他等待救援地区，车辆装运物资耗费的时间很大，因此需要对物流园中心在实际工作中接收物资的服务系统进行优化。根据一般排队系统的构成，包括顾客、服务机构和排队规则，可以将车辆排队调度物资系统中排队现象抽象为相应的排队系统。应急物流系统中的物资运载车辆相当于顾客，接受车辆的服务台相当于服务机构。

2.2 案例描述

以武汉市宝湾物流园中转站为实际案例，园区内有一片醒目的被涂为红色的隔离区，这是运货司机的专属地点，运输物资的车辆到达中转站后，将车辆停在卸货区，再去隔离区休息，卸货完成后，会有工作人员通知司机到卸货区提车并离开，实现了全程“零接触、“全流程、全链条”安全顺畅。

根据来源于武汉市交通运输局的数据显示，自2020 年1 月23 日至3 月15 日，铁路向武汉运输货物1 906 车、64 452.1吨；累计完成各地支援人员运输任务6 761 人次。武汉天河国际机场共保障航班1 818 架次、运输4.96 万人、货物12 225 吨。武汉公交集团运送人员111.4 万人次、物资280.2 万箱（件）。武汉港航发展集团运送人员13.7 万人次、物资0.71 万吨。出租汽车安排车辆6 000 辆，运行53.4 万辆次。安排邮政、快递车辆出入武汉39 178 辆次，助运医疗防护等应急物资约17.91 万吨；累计收件673 万件、派件1 180 万件。武汉港货物吞吐量445.01 万吨，集装箱吞吐量5.44 万标箱。

由上述案例分析，自2020 年1 月23 日至3 月15 日，5 个物资中转站累计接收物资超5 000 吨，根据统计数据计算大约有566.497 7 万吨货物，物流中心大货车平均标准荷载量为18.75 吨/辆，24 天时间约有296 799 辆货车进入物流园，5 个物流转运站平均分别每天有2 474 辆车进入，可得平均每小时有104 辆车到达。假设车辆的到来服从泊松分布，物流中转站服务台平均每小时可服务120 辆车，服务时间服从负指数分布。

（3）传统的热水系统受能量转换效率的限制，制热效率均小于1；而空气源热泵热水系统仅需通过消耗少量的高品位能便可驱动制冷工质吸收空气中大量的低品位能，制热效率可达到3～5。

2.3 假设条件

针对排队论模型有以下假设：

（1）输入过程：假设运送物资的车辆到达物流中心的概率分布为服从泊松分布，且车辆到达是相互独立且平稳的。

（2）排队规则：排队系统中车辆排队和等待服从等待制规则，即先到先服务。

（3）服务机构：假设排队系统中有1 个或多个服务台，而且服务时间是平稳的，服从负指数分布，任意2 个车辆卸载物资的服务时间是相互独立的。

2.4 模型建立

这里建立车辆运输物资到物流园地点的排队论模型，每辆来车到达物流园外，并排队进入指定地点卸货，假设有1 个服务台接受物资，构成M/M/1 排队模型，卸完一趟物资离开以便下一辆车接受服务。如图1 和图2 分别为运载物资车辆的一般排队模型和M/M/1 排队模型。车辆接受服务过程服从M/M/1 的排队模型，第一个M 指车辆到达流或车辆到达间隔时间的分布；第二个M 指物流园服务时间的分布；1 或C 指服务台的个数。

图1 运载物资车辆的一般排队论系统

图2 Flexsim 中M/M/1 模型构建

2.5 指标计算

通过以上案例分析中的数据，计算得到每分钟到达的平均车辆数λ=104 辆/小时，每分钟服务的车辆数μ=120 辆/小时，服务强度为ρ=λ/μ=0.867，说明服务台有86.7%的时间在服务，有13.3%的时间是空闲的。

M/M/1 排队模型的各运行指标公式如下：

式中：Ls表示系统内车辆数（包括正被服务的车辆和排队等待服务的车辆）的数学期望；Lq表示系统内等待服务的车辆数的数学期望；Ws表示车辆在系统中逗留时间（包括排队时间和被服务时间）的数学期望；Wq表示一个车辆在系统中排队等待时间的数学期望。将数据代入各运行指标计算得表1。

由表1 数据可知，仍需要提高红十字会中心的服务水平，缩短车辆在系统中的平均逗留时间，缩短顾客平均排队时间和平均服务时间。有两种模型优化措施可以选择：第一，缩短服务时间，提高服务率μ；第二，增加服务台数量C，即增设服务窗口。

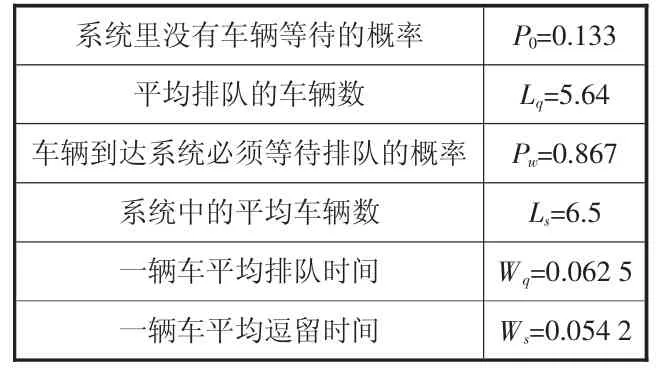
表1 M/M/1 模型

3 应急物资调度排队论模型优化

3.1 缩短平均服务时间

使每小时服务的车辆数由原来的120 辆增加到130 辆，这时的λ 仍然是104 辆/小时，μ 变成了130 辆/小时，由运行指标公式计算结果如表2 所示。

根据表2 运行指标数值，发现提升服务率μ 后，一辆车平均逗留时间和平均等待时间有一定程度减少，因此提高服务强度即通过增加卸货工作人员的数量、增加叉车的数量等措施有助于提升应急转运效率。

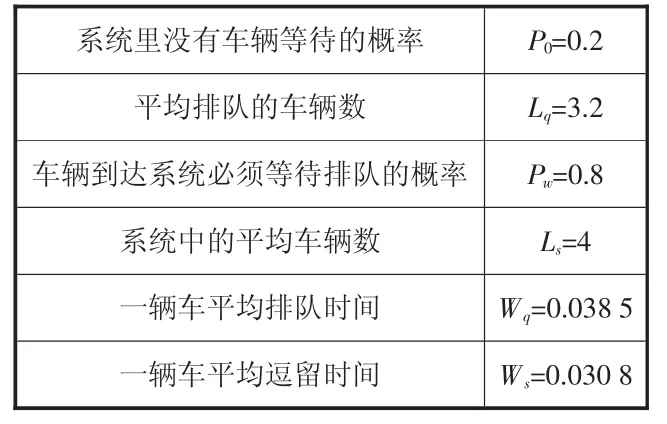
表2 缩短平均服务时间后M/M/1 模型

3.2 增设服务窗口

3.2.1 M/M/3 模型

增加服务台的数量为3 个窗口，排队模型变为M/M/3，排队规则为一共排1 队，ρ=λ/cμ，先到先服务。运载物资车辆的M/M/3 排队模型如图3 所示。

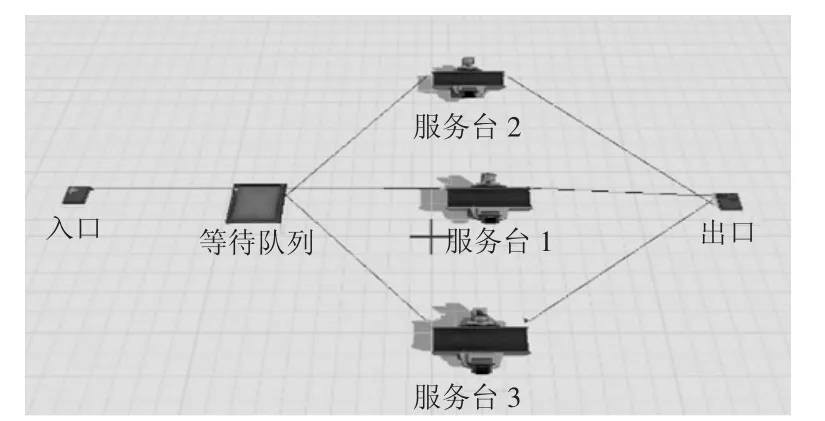
图3 Flexsim 中单队列M/M/3 模型构建

模型改变后的运行指标公式为：

式中：Ls表示系统内车辆数（包括正被服务的车辆和排队等待服务的车辆总和）的数学期望；Lq表示系统内等待服务的车辆数的数学期望；Ws表示车辆在系统中逗留时间（包括排队时间和被服务时间总和）的数学期望；Wq表示一个车辆在系统中排队等待时间的数学期望。

利用上面指标公式计算结果如表3 所示。

由表3 数据可知，增设服务窗口后，发现各个指标有所降低。说明通过增加服务台的数量，可以缩短车辆平均排队时间和平均等待队长，使得物资调度效率提高。

表3 单队列M/M/3 模型

3.2.2 3 个M/M/1 模型

如采用第二种方法，将服务窗口增加为3 个，排队模型为3 个M/M/1，采取每个窗口排一队的排队规则，一共排3 队，λ=104/3=34.67，先到先服务。运载物资车辆的3 个M/M/1 排队模型如图4 所示。利用公式计算各指标得到数据如表4 所示。

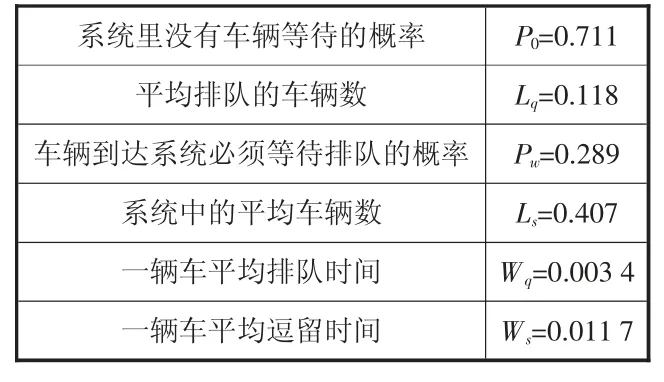
表4 多队列M/M/3 模型

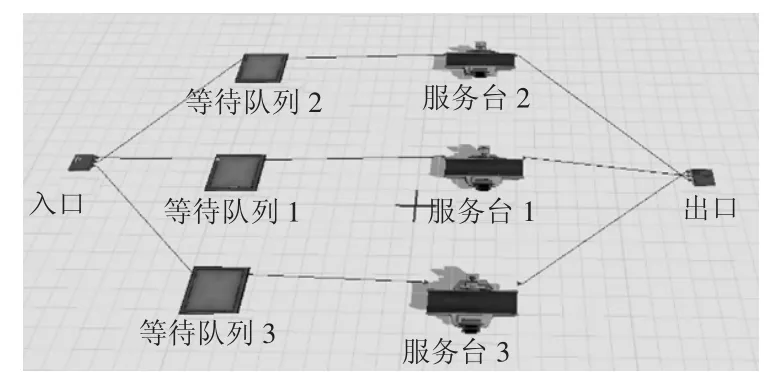
图4 Flexsim 中多队列M/M/3 模型构建

由表4 数据可知，增设服务窗口后，多队列各个运行指标比单队列时的指标值有所提高。说明多队列M/M/3 的排队模型不利于提高调度效率，增加服务窗口后排单队列效率更高，单队列M/M/3 模型更优。

3.3 结果比较分析

由表5 各种排队模型的运行指标不难看出，一个M/M/3 排队模型比3 个M/M/1 排队模型构成的排队系统效率更高。因此，在服务台个数和服务率都不变时，单队时等待队长、等待时间都比多队时低，且服务台的利用率都比多队时高，单队排队模型具有明显的优势。

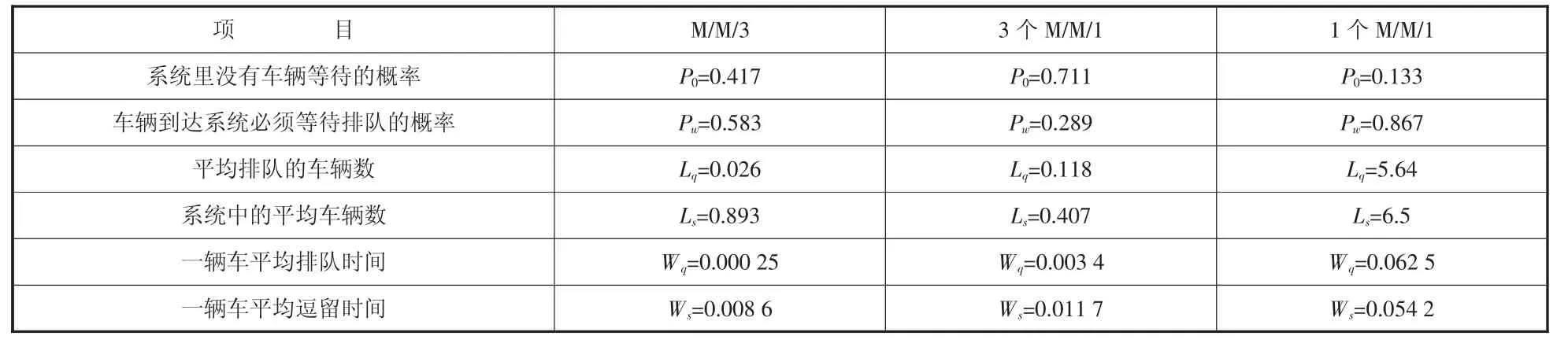
表5 M/M/3 和M/M/1 模型比较

综上，由表5 给出M/M/3 和3 个M/M/1 模型指标计算值比较，可知当增加服务台的个数，且服务率和服务台数不变时，单队列排队模型的排队时间更短、平均排队的车辆数更少。即增设服务台后，服务率和服务台个数都不变的情况下，排列单队比排列多队服务效率更高。因此，在对物流转运中心排队系统优化时，可以采用多服务台单队列的方式对运载物资的车辆提供服务。

4 结论、不足和展望

结论：根据M/M/1、M/M/3、3 个M/M/1 三种排队模型的指标结果，在实际车辆被服务过程中，若不改变服务台个数，可以用增加卸货人员的数量、增加叉车方法提高服务率μ，进而提高物资转运的服务效率；增加服务台个数时，可运用排一队的M/M/C 方法来缩短排队时间，从而提高物资转运的调度效率，本文研究结论可以解决新冠肺炎疫情期间的应急物资调度慢等问题，为救助灾民节省宝贵时间。同时，通过此研究过程及结果对其他涉及到排队模型的物资调度问题提供了理论和优化方案。

不足与展望：

（1）本文根据搜集到的相关数据进行理想化的假设，得到的结果可靠性有待验证，但它符合排队论模型优化的一般结论，可以作为未来应急物流基地中心的车辆排队问题的优化依据。

（2）今后还需要搜集车辆到达时间间隔的实际数据，以及服务的时间间隔数据，运用Flexsim 软件进行模拟仿真的结果会更加准确。

（3）改进的智能算法、启发式算法、遗传算法正在兴起，在各种优化问题的应用中体现了准确性和有效性。未来与已有算法结合的混合算法，将其应用在应急车辆调度优化问题上有很好的前景。

（4）信息化时代，云物流是一种新的物流模式，其理念是以物流信息平台的形式整合物流资源，使物流资源合理配置。实现应急物流的相关多方主体进行物资调度的全程信息协同，工作人员通过物联网、可视化技术、云计算平台、人工智能等，可实时监测各灾区物资需求变化与车辆在道路运输情况，按需在车辆中心调度一定数量转运车辆，避免运载物资车辆数大于接收物资车辆数，从而为应急物资调度减少不必要时间损耗。今后应结合新兴的算法和信息化技术等继续深入研究应急物资调度等一系列问题，以期为后续学者的研究带来理论依据，并且推动应急管理实践的不断进步。