基于自适应粒子群算法的电动汽车充电桩布局优化

江晋剑，朱纬纲

（安庆师范大学 计算机与信息学院，安徽 安庆 246133）

世界能源短缺问题日益严重，各国都在寻找更加环保的能源解决方案。2021年北京市印发的《“十四五”时期国际科技创新建设规划》文件强调，积极推进先进储能，助力国家2060年前实现碳中和战略目标。电能作为一种清洁能源，已成为我国能源的重要组成部分[1]。同时，电动汽车作为传统汽车的有效替代品，可以有效缓解我们对石油的依赖，并减少温室气体排放。在电动汽车普及初期，由于缺少一套科学完善的充电桩布局规划指南，还没有形成科学的充电桩布局体系，导致充电站的选址规划不合理，导致用户体验较差[2]。如何更加合理地确定充电站位置和充电桩数量，是目前一个急需解决的问题。针对这一问题，国内外学者已经提出了一些方案。例如，IOANNIS等[3]采用一种新的排队模型对快速充电站进行了分析，其按照汽车电池大小进行分类，通过考虑可用的充电点，以及各种电动汽车随机到达过程和随机充电需求来计算客户在队列中的平均等待时间。WANG等[4]提出了一个综合考虑电动汽车可持续发展、充电站特征、充电消费者特征、充电需求分布、电网和城市规划等因素的电动汽车充电站布局多目标规划模型，然后根据需求优先级和现有加油站的使用情况设计求解算法。HARIS等[5]采用中位数选址模型来解决了土耳其一家网络公司的充电站设计问题。加鹤萍等[6]以充电站收益最大化为目标函数，以交通流量为约束目标，运用模拟退火算法进行了最优求解。贾永基等[7]基于满意优化理论，提出了电动汽车满意度评价函数，并运用免疫算法进行了最优求解。杨军峰等[8]将每个区域中心作为电动汽车充电负荷中心，采用TLBO优化算法计算出了电动汽车充电站的数量。耿建超等[9]建立了日常出行模型以模拟电动汽车用户充电需求，从宏观角度规划充换电站的布局。肖白等[10]提出了一种在备选站址既定情况下含不同容量充电桩的EVCS选址定容优化方法，并结合模拟退火算法和迪克斯特拉算法对模型进行了最优求解。梁迪[11]等以各需求点的需求度权重以及充电站到需求点距离的乘积之和最小为目标构建了选址优化模型，并采用了鲸鱼算法（IWOA）来求解。邹云程[12]等分析了充电技术发展对充电设施布局的影响，构建了考虑充电选择的电动汽车均衡交通分配问题模型，通过算例分析验证了所提模型与算法的有效性。刘蕾[13]等将学校设为研究对象，利用求出的日充电需求、充电负荷曲线图等以成本最低为目标建立模型，并用整数规划分枝定界法对该模型求最优解。

虽然现阶段已有很多关于充电基础设施的空间选址规划方案，但其大多是从成本、已有电网等角度出发，在现实情况下，由于数据量较多，导致算法复杂度高且模型求解难度大。因此，本文以某市为例，采用Folyd最短路径算法对待分配充电桩节点进行了选址约简，并使用自适应粒子群算法对模型进行最优求解，以期得到该区域充电站合理的位置布局。

1 充电站选址模型构建与算法应用

2 基于Floyd最短路径的选址约简

弗洛伊德最短路径算法（Floyd）[15]是网络流算法的一种，常用于各种中心选址问题的分析，用以实现中心到各节点的距离最小，从而达到经济效益最优。在道路情况复杂、路口节点较多的情况下，由于数据繁多，对每个道路节点进行建模计算的工作量较大。因此，本文采用Floyd最短路径算法对道路节点进行约简，只选择到每个节点曼哈顿距离最小的中心节点进行建模计算，即可保证在时间成本最小情况下实现科学选址。该方法基本思想是，先把带权邻接矩阵A作为距离矩阵D的初值。

当k=n时，Dn=中便是允许中间点为ν1,ν2,ν3,…,νk的，从νi到νj路径中的最短路径长度，即是求从νi到νj中间可插入任何顶点的路径中最短路径长度，因此Dn即为距离最短矩阵。矩阵Dn的每个元素都代表了两点间考虑了其他任意点作中间点时的最短距离，最后将Dn中的各行元素求和，即可得到每一个点到其他各点的最小距离和，因此通过比较即可筛选出多个充电桩选址，在面临数据量较大的选址问题时，这一操作能够降低计算成本，减少问题复杂度。

3 自适应粒子群算法

4 算例分析

本文以美国南达科他州最大的城市苏福尔斯为例，该区总面积80万平方英里，路口节点24个，规划在此区域内建立多个电动汽车充电桩。算法参数：种群规模为50，学习因子c1，c2取1.496 2，惯性因子wmax为0.9，wmin为0.4，迭代次数取250次。根据上文的模型构建，在充电站候选点生成后再对其进行编码，随机生成充电站选址种群，并依次对每个个体的目标函数进行计算，且对总成本最低的个体给予更高的适应度，同时进行选择、交叉、变异遗传操作以产生下一代个体，直到到达设定的最大迭代次数，从而得到充电桩最优布局。通过对该市车流量信息的调查，获得该区域的日平均车流量见图2，路口节点坐标见表2。

表1 充电站/车辆参数数据

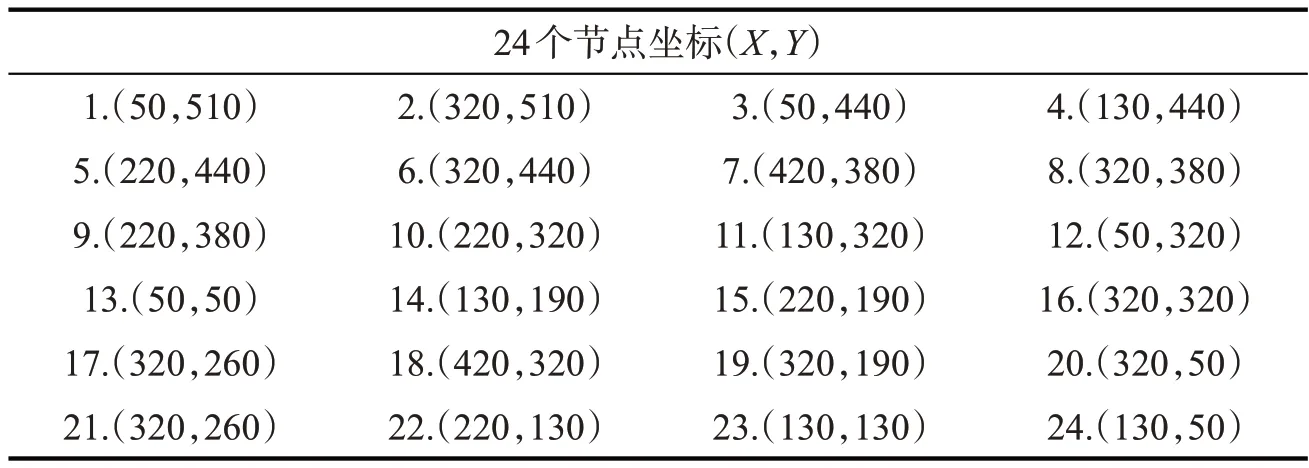
表2 节点坐标表

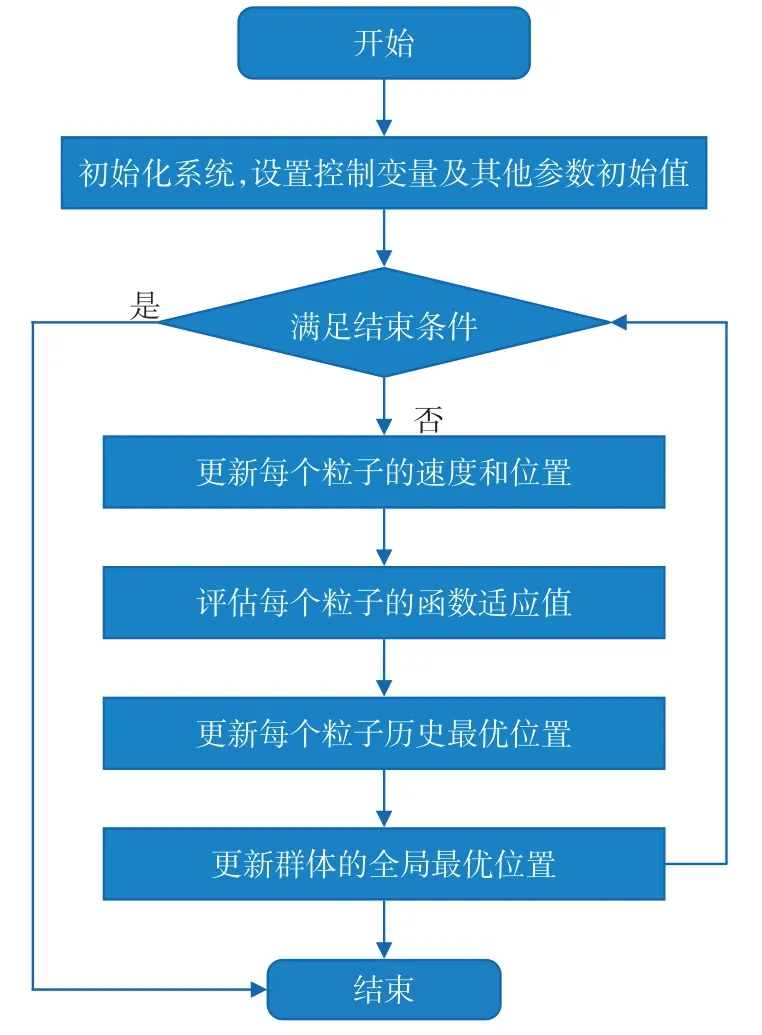
图1 基于自适应粒子群优化算法的电动汽车充电站选址布局流程

5 仿真实验

通过MATLAB2019 计算得到了24 个候选节点的路径矩阵，将矩阵的行元素求和后，得到了表2中24个候选节点到各点的最小距离和，如表3 所示，可见1、2、6、13、20、21、24号节点到各节点的距离之和的大于最小距离之和平均数，因此该7个节点在仿真实验中不参与模型求解，并将其余节点作为充电站候选点，具体节点之间的位置关系如图3所示。

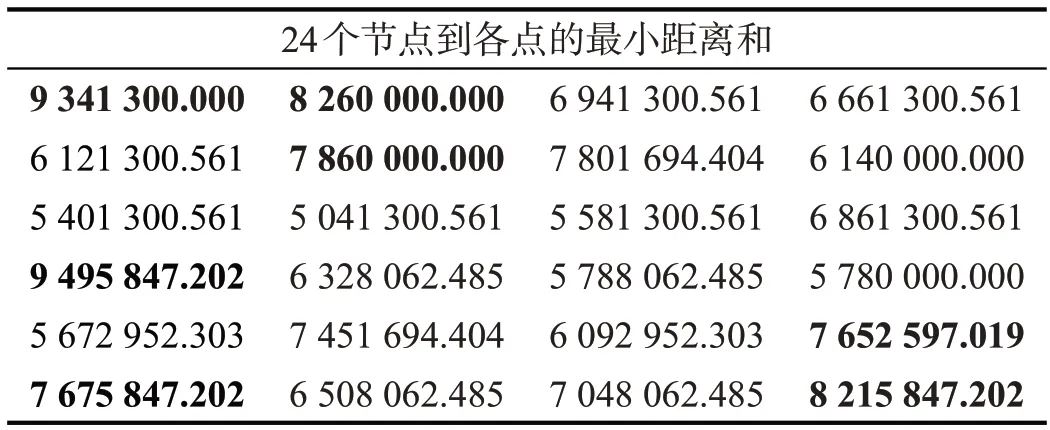
表3 候选节点到各点的最小距离表

图3 Folyd算法选址约简

为了验证算法的优化能力，本文分别采用了标准粒子群算法（PSO）和自适应粒子群算法（CPSO）对该算例进行最优求解，得出了两种算法的最佳适应度值图像（图4）。对比图中的两条曲线可知，PSO在迭代到135次时收敛，CPSO在迭代到88次时收敛。在迭代初期，PSO 收敛的性能优于CPSO，而CPSO 在迭代的中后期仍保有较好的种群多样性，并于较少的迭代次数时收敛，其综合优化结果优于PSO，其充电站位置如图5所示。

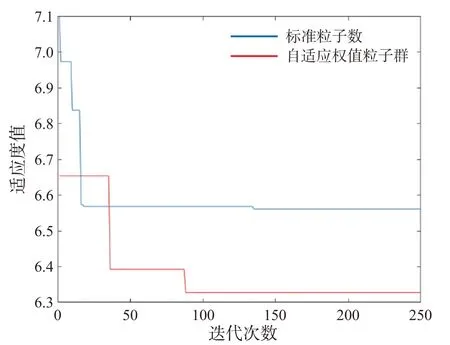
图4 算法结果对比

图5 充电站最优布局

6 结论

优化电动汽车充电站的布局是一项具有长期性和复杂性的工程。本文在该方面取得了一些阶段性研究成果，但依然存在一些问题值得探讨。本文模型适用于新能源电动汽车充电站布局规划问题，实现在综合成本最低与节约资源的前提下进行充电桩布局。通过Floyd 算法求解距离矩阵，快速找到多源点之间的最短路径，并选取最优节点作为充电桩的待建点，能够有效减少计算成本。在粒子群算法（PSO）基础上，对惯性权重的取值进行了改进，改进的粒子群算法（CPSO）有效地提高了迭代速率，使其能更精准地找到最优适应度值。通过仿真计算发现，该方案能为电动汽车提供良好的服务，同时能够避免充电站无序安装所带来的社会资源浪费，对城市充电桩最优位置的规划具有指导意义。当前国内外充电站的建设均处于起步阶段，充电站建设区域的用地面积也只能大致估算，模型在许多方面有待完善。一些理论数据与实际情况仍存在偏差。后续还可增加季节、天气、汽车品牌类型、用户充电习惯以及电网负荷等因素，从而使所建模型更能贴近实际情况。