孪生网络融合卡尔曼滤波的目标跟踪研究

任奕颖，董小明

（安庆师范大学 电子工程与智能制造学院，安徽 安庆 246133）

随着智能交通、视频监控和人机交互等领域的不断发展，目标跟踪逐渐成为计算机视觉领域的热门研究方向之一。近年来涌现出很多优秀的算法，相比过去已取得了很大突破，但如何在运动模糊、遮挡、光照变化等干扰下保持跟踪算法的准确性，仍是尚待研究的问题。

当前目标追踪算法的研究热点方向主要有两类。一类是基于相关滤波的跟踪算法。自从提出相关滤波追踪方法后，因其性能和速度优势，在目标追踪领域受到了广泛的关注，在跟踪的精度及速度方面有很大提升，但相关滤波法随着研究的推进，在精度提升上遇见了瓶颈[1-5]。另一类是基于孪生网络框架。基于孪生网络（Siamese Network）的目标追踪算法由于其在速度和准确度方面上能取得相对平衡，故引起了广泛关注。SiamFC[6（]Siam Full Convolution）算法采用相似性函数设计以计算模板区域与搜索区域之间的相似度，从而得到所跟踪目标的位置及大小，这种方法虽然在速度上取得了很大提升，但难以解决长时间跟踪后的目标偏移及丢失问题。SiamRPN[7（]Siam Region proposed Network）模型在孪生网络的输出后加上区域建议网络，通过联合训练分支和回归分支进行区域建议，将跟踪任务转换为检测任务，在保持精度的同时实现了高速跟踪。然而，当目标快速移动或有遮挡干扰时，其容易出现目标丢失情况。ZHU等在SiamRPN结构上提出了DaSiamRPN模型[8]，通过在训练阶段增加负训练样本以增强数据，使得结果更具有鲁棒性。BO等在SiamRPN结构上设计了SiamRPN++模型[9]，通过随机移动训练目标在搜索区域中的位置以消除中心偏差，并对网络结构进行了优化，使跟踪精度达到更高的深度网络结构。然而在长时间跟踪中，Siamese类跟踪器对于目标全遮挡和运动模糊等情况处理效果不佳。为了改善长时间目标跟踪易出现的跟踪偏差问题，本文在孪生网络跟踪基础上，设计了一种孪生网络结合卡尔曼滤波[10-11]的方法，以期改进跟踪效果。改进的孪生网络以SiamRPN为基础，在视觉信息输入时，利用卷积神经网络对模板帧和检测帧进行特征提取，再通过区域推荐网络来获取位置坐标和跟踪目标的尺度，其后将结果传递给Kalman滤波器，通过上下帧的关联来提高跟踪的稳定性。卡尔曼滤波模块能够根据预测能力在目标受到环境噪声影响时，对目标位置进行更精确的跟踪，使得跟踪精度更高。

1 跟踪框架

1.1 孪生网络框架

孪生网络[10-12]类跟踪算法由模板分支和搜索分支两部分组成，如图1所示。算法求取目标相似性分数的过程可以抽象为f(z,x)=g(φ(z),φ(x))。其中，z为模板分支特征，x为搜索分支特征，φ(·)为特征表达函数，g(·,·)表示算法的映射变换，f(·,·)表示相似性分数。跟踪时通过共享参数的主干网络来提取特征，然后经过核心跟踪算法处理以获得目标在分数响应图中的位置，最后通过映射关系来得到目标在真实视频帧中的位置和轮廓大小。

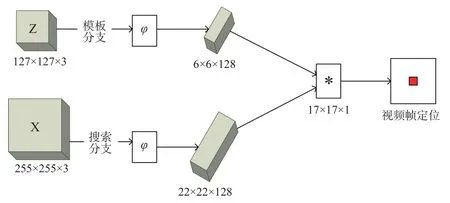
图1 孪生网络类跟踪框架

1.2 孪生网络改进

改进的孪生网络以SiamRPN 为基础，SiamRPN 方法把第一帧作为模板，将其与检测帧分别通过结构和参数完全相同的AlexNet网络以形成两条支路来进行特征提取，然后经过区域候选网络卷积运算来分别得到分类分支和回归分支结果。本文在特征提取部分进行了改进（图2），主干网络以残差网络为基础，加入了空洞卷积金字塔池化过程，即ASPP（Atrous Spatial Pyramid Pooling）[13]模块以加大感受野，从而增加全局信息。

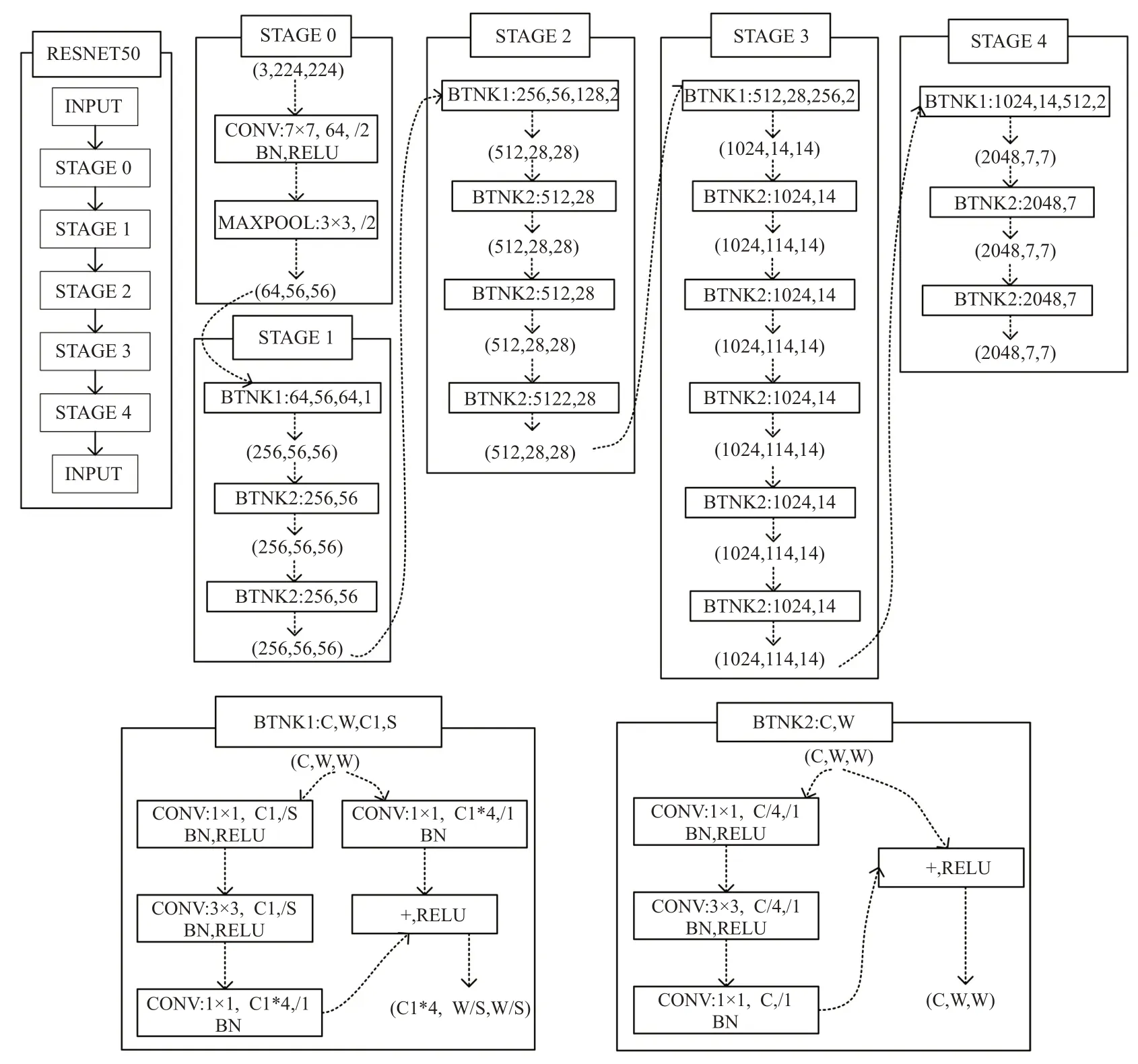
图2 Resnet网络结构

整体的孪生网络框架如图3所示，将模板图像和搜索图像输入到左边的孪生网络中进行特征提取，并将提取到的信息输入区域建议网络（RPN网络），从分类分支得到目标前景背景区分，从回归分支得到目标边界框较精准位置。

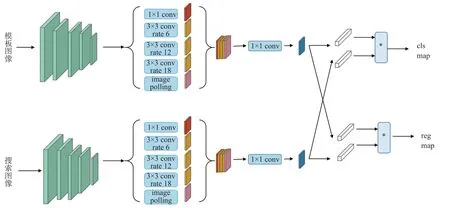
图3 改进的孪生网络结构

1.3 融合自适应卡尔曼滤波

目标跟踪涉及时间和空间维度，如果结合历史帧所跟踪的目标轨迹信息，能进一步提升跟踪效果。本文利用卡尔曼滤波器将目标的时间轨迹信息与跟踪器信息进行整合。经典的卡尔曼滤波在面临跟踪过程中非线性轨迹变换时，存在明显的缺陷。卡尔曼滤波稳定跟踪要求所跟踪目标的数学模型必须精确，不合适的噪声模型设定将导致跟踪精度的下降，甚至引起滤波器的发散。当卡尔曼滤波器达到稳态时，卡尔曼增益趋于稳定。如果目标状态突然改变，卡尔曼滤波器不能很快地调整增益，并将导致滤波器的发散。针对传统卡尔曼滤波方法的不足，本文设计了一种自适应卡尔曼滤波方法来抑制干扰，以期克服目标快速运动过程中的跟踪不稳定性。通过引入一个调整因子，可以在线调整滤波器增益矩阵，从而快速、平稳地调整滤波器。

传统的卡尔曼滤波器有时间更新和观测更新两个更新过程。时间更新主要用于系统的预测，包括状态预测和协方差预测。观测更新包括卡尔曼增益的计算、状态更新和协方差更新，称为校正阶段。在系统预测过程中，利用对当前状态的观测来修正预测值。状态预测可表示为xk|k-1=Ckxk-1|k-1+BkUk，其中，xk|k-1是对以前状态的预测，Ck是状态转移矩阵，Bk是系统参数，Uk是进程在k时间的控制量，如果不存在控制，其可以为零。卡尔曼滤波器的状态x由目标的位置x、y和速度νx、νy组成。时间k的残差可以表示为Vk=Zk-Hxk|k-1，其中，Zk是时间k的观测值，H是观测矩阵。协方差预测过程用于预测状态的协方差，表示为Pk|k-1=λkCkPk-1|k-1+Qk，其中Pk|k-1是对状态xk|k-1的协方差预测，而Qk是系统进程的协方差矩阵。λk是Pk-1|k-1的调节因子，在卡尔曼滤波器中λk=1。下一步是观测更新，首先计算状态更新和协方差更新的卡尔曼增益，然后得到电流状态的观测值。状态更新可以通过对当前状态的最优状态估计来实现，包括预测值、观测值和增益。卡尔曼增益的定义是Gk=Pk|k-1HT(HPk|k-1HT+RK)-1，其中，Gk是卡尔曼增益，H是观测矩阵，Rk是测量噪声的协方差矩阵。状态更新过程表示为xk|k=xk|k-1+Gk(Zk-Hxk|k-1)，其中，xk|k是最优状态估计，Zk是观测值。协方差更新表示为Pk|k=(I-GkH)Pk|k-1(I-GkH)T+GkRk，其中I是单位矩阵。

卡尔曼滤波与自适应卡尔曼滤波的主要区别在于Rk，Qk和λk。Rk和Qk在卡尔曼滤波器中是固定的，其有效性取决于Rk和Qk的初值。因此，我们引入了自适应滤波器对卡尔曼滤波器的更新过程。Rk=μRk-1+(1-μ)[-HPk|kHT]，Qk=μQk-1+(1-μ)[+Pk|k-CPk-1|k-1CT]，其中μ是Rk和Qk的衰减因子。实验表明，μ值过大会导致严重的滤波器漂移，因此其应该满足0 ≤μ≤0.1。λk大小影响Pk|k-1和Gk的大小。通过在线调整λk值，设计了合适自适应卡尔曼滤波器，以满足E[]=0。设计λk是为了消除时间k的残余误差。当k变大时，λk值受残差协方差的影响会变小。因此，噪声对滤波器的影响不大，预测曲线变得平滑。随着时间推移，残差期望值趋于零。通过上述方法，可以快速平稳地调整滤波器。

2 算法设计及结果分析

2.1 算法流程

本文算法的目标跟踪过程：首先，初始化系统，在修改卡尔曼滤波器系统状态初始值和初始预测的同时，将初始框的中心和位置赋值给改进版SiamRPN和卡尔曼滤波器。随后，孪生网络通过特征提取、分类回归和分支回归，最终得到位置坐标和跟踪目标的尺度，并向卡尔曼滤波器传递结果，自适应卡尔曼滤波根据上一帧的信息来相对准确地预测当前帧目标中心点位置，并重复上述过程，实现目标跟踪（图4）。

图4 本文算法流程图

2.2 定性分析

本实验从OTB100[14]中选取了6组代表性视频：Bluecar、Jump、Human、Suv、Trellis和Man，分别对应运动模糊、遮挡、光照变化等情况，以期验证本文算法的有效性。图5中Bluecar和Jump视频序列主要针对运动模糊情况，可以看出，本文算法可以在当车辆行驶过程出现模糊时准确跟踪目标，也可以在运动员因跳高快速移动而出现模糊和尺度变化时精准锁定运动员，不会出现目标丢失的情况。

图5 不同情况下的跟踪效果图。（a）画面模糊情况下的Bluecar跟踪效果；（b）快速运动下的Jump跟踪效果；（c）部分遮挡时的Human跟踪效果；（d）画面昏暗情况下的Suv跟踪效果；（e）色彩单调时的Trellis跟踪效果；（f）光线变化人脸跟踪效果

Human和Suv视频序列主要针对目标遮挡情况，由图可知，行人经过路牌时上半身被遮挡，本文算法可以准确跟踪到显露出来的双腿，并在行人重新出现时准确地跟踪。车辆经过树冠、只剩下小部分车身时，本文算法也可以将其准确定位，并在车辆再次出现时，重新定位。Trelliis和Man视频序列主要针对光照变化情况，由图可知，本算法可以在光线由暗转亮或由亮变暗等不同亮度变化情况下准确跟踪到目标。以上结果表明，本文所提算法可以有效适应光照变化、运动模糊、遮挡等复杂环境，证明了本文算法在应对复杂环境情况时具有较强鲁棒性。

2.3 定量分析

跟踪定量比较实验在视觉目标跟踪标准平台OTB100 测试集中进行，该测试集评估指标包括精确度和重叠率等。本文对多种算法进行对比[14]，并重点标注表现良好的前十种算法，其中Muster算法[15]是利用长短期记忆来学习的神经网络算法，还有其他排名靠前的相关滤波类算法，在标准平台的对比结果中表现都低于孪生网络算法[14]。同时我们设计的算法在精确度和成功率方面都有良好表现，超过孪生网络代表算法SiamRPN[7]。精确度指标表示所跟踪区域的中心值与所标注的真实区域中心值的距离。显然，若所要求距离越近，跟踪结果视频中能达到此要求的帧数越少，而所要求距离越远。则能达到要求的帧数比例越高。跟踪精度如图6所示，其横坐标是位置误差阈值，纵坐标是在误差允许范围内跟踪成功帧数所占总帧数的比率，曲线整体走势是随着误差阈值要求放宽，整体符合要求的帧比例走高。图中清晰反遇出，SiamRPN相对传统算法[14]已经表现不俗，经过改进后，可进一步提升精度效果。在目标跟踪研究中，重叠率是另一个重要衡量指标，表示所跟踪的目标面积与目标实际标注面积的比值。显然，重叠率越高则表示跟踪效果越好，理论上跟踪位置与真实位置完全重合即重叠率为1时是跟踪的完美情况。图7的横坐标是重叠率阈值，纵坐标是在此重叠率标准下视频中能成功跟踪的帧数与总帧数比例。显然，重叠率要求越高，则整体成功率会随之降低，所以图7的曲线整体走势是逐步降低，本文所设计的算法在整体表现上也超越了SiamRPN和传统算法。

图6 算法精度对比

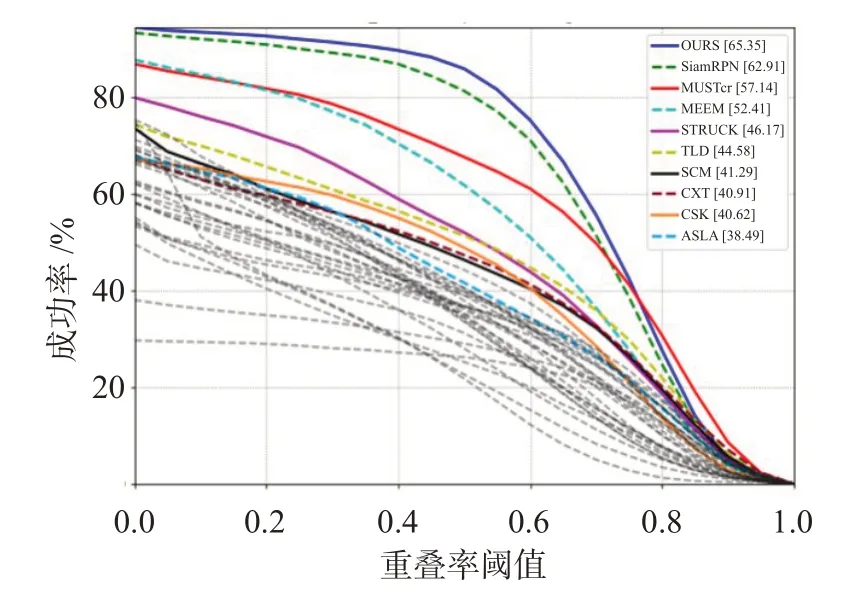
图7 算法成功率对比

3 结束语

本文提出了一种目标追踪算法，其结合卡尔曼滤波器改进了SiamRPN模型，改进后的SiamRPN模型分别通过对模板帧和检测帧提取特征，因深层的残差神经网络能获得更精确的目标特征，从而提高了对目标的有效识别和定位。同时，卡尔曼滤波模块利用目标轨迹关联特性，提高了目标受到干扰或遮挡时的稳定性，并提高了跟踪精度。后续研究将在特征选择网络结构和滤波策略两方面进行改善。