基于排队论的战时装备维修保障人员需求确定方法

赵陆昊，阮拥军，张耀龙

（陆军工程大学石家庄校区装备指挥与管理系，石家庄 050003）

0 引言

随着科学技术的发展，武器装备科技含量不断增加，故障维修难度增大，使得战场抢修任务复杂繁重。装备维修保障人员是完成装备维修保障任务的基础，是装备维修保障力量体系的重要组成部分。目前部队的装备维修保障人员在数量上与所担负的战时装备维修保障任务还不能良好适应，降低了装备维修保障效能。如果未经科学决策而确定装备维修保障人员数量，可能会导致任务无法如期完成或造成人力资源的浪费。因此，如何针对战时装备维修保障任务需求配备合理的装备维修保障人员，对于做好战时装备维修保障工作具有重要的现实意义。

许多学者在装备保障人员需求方面开展了研究。文献［1］基于案例推理方法，并在案例检索过程中引入BP 神经网络的相关原理方法，从以往实际经验中推算出装备保障人员需求情况。文献［2］在将装备保障任务分类的基础上，针对每类保障任务的特点，确定不同的保障人员需求预测方法。文献［3］分析了装备维修保障人员构成的随机服务系统特征，运用排队论理论建立了以平均等待时间为目标的维修人员需求模型，得出各专业对维修保障人员的实际需求。但这些文献只针对平时的装备保障，并没有考虑战时实际情况，所提出的装备保障人员需求确定方法不具备说服力。因此，为了解决战时装备维修保障人员需求问题，本文考虑到战时装备维修保障的不同方式，从任务需求的角度出发，通过构建基本维修单元，并基于排队论建立装备维修的排队系统，对所需要的基本维修单元数量进行计算，从而确定装备维修保障人员需求数量，为部队装备维修保障力量体系规模设计提供参考。

1 问题描述

1.1 基本维修单元

由于现代武器装备结构功能的复杂程度不断增大，战时装备维修保障任务需要多种专业的维修人员共同协作来完成。对维修人员合理编组，以模块化形式构建基本维修单元，可以更好地适应战时装备维修保障任务。同时，可将基本维修单元看作服务台，便于排队系统的建立。

基本维修单元是指能够独立完成规定维修任务的最小保障资源的组合单位［4］。根据基本维修单元的定义，基本维修单元是根据执行任务所需能力进行构建的，其组成应包括完成规定维修任务所需的最少资源，由维修人员、保障装备、维修设备及器材等按规定要求组合而成。本文研究的是装备维修保障人员需求，因此，只考虑基本维修单元内的人员情况。在人员类别上，基本维修单元内应包含全部维修任务所需的人员类型；在人员数量上，应配置每类维修任务所需的维修人员最大值。因此，基本维修单元内的装备维修保障人员可按以下方法来确定［5］：假设某次作战中共有R（R=1，2，…，i）种可能的装备维修任务，装备维修保障人员中有D（D=1，2，…，j）种专业，xi，j为执行第i 种维修任务需要的第j 种维修专业人员数量，则每种维修任务所需的维修人员数量为：

构建基本维修单元所需的装备维修保障人员为：

1.2 装备维修保障方式

组织战时装备维修保障时，在保障方式上，主要以伴随保障与定点保障两种方式相结合。其中，伴随保障是在每个作战单元中配置一定数量的基本维修单元，伴随部队行动实施装备维修保障的方式，主要是对故障装备迅速地实施救、修、供，使其保持连续的作战能力，具有与保障任务相适应的能力。定点保障是根据需要在便于实施保障的地点开设装备维修保障机构，对一定范围内的部队和过往部队实施装备维修保障的方式，是装备维修保障的基本方式之一，主要是对伴随保障无法修复的故障装备进行维修［6］，如图1 所示。

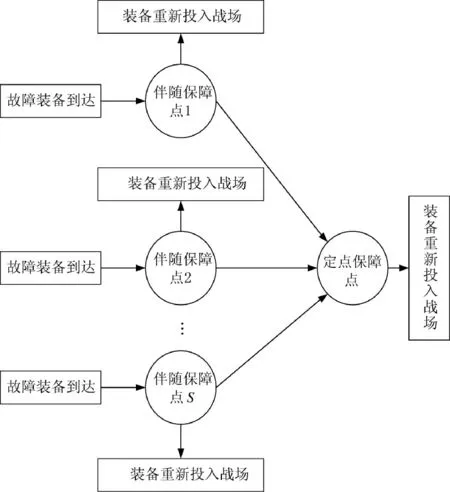
图1 伴随保障与定点保障关系Fig.1 The relationship between accompanied support and fixed-point support

1.3 确定战时装备维修保障人员需求的总体思路

根据战时装备维修保障实际，不同的场合运用装备维修保障人员的方式不同，有的伴随作战单元实施抢救抢修工作，有的在固定保障点开展维修保障工作。为确定装备维修保障人员数量，区分伴随保障和定点保障两种场合下的主要装备维修保障任务，对装备维修保障人员编组，构建基本维修单元，以基本维修单元为单位执行装备维修保障任务。应用排队论对执行任务的过程进行分析，将基本维修单元视为服务台，每个保障点配置的基本维修单元数量为服务台数量，基本维修单元执行装备维修任务的过程，理解为装备维修任务排队通过服务台即基本维修单元的过程，故伴随保障、定点保障均可和与它们相应的装备维修任务联合起来构成排队系统。由于两种保障方式下的任务需求不同，对伴随保障的排队系统以持续参战率为衡量标准，定点保障的排队系统则以故障装备等待维修时间为衡量标准，并以装备数量、故障装备到达速率、故障装备修复率作为已知条件，对这两个衡量标准进行计算，选取最优值，最终得到所需的基本维修单元数量，即装备维修保障人员数量。

2 排队系统的建立

2.1 排队系统的基本特征

1）输入过程。其主要是指故障装备到达排队系统的间隔分布规律。在作战中，装备发生故障有以下规律：作战单元内的装备发生故障是随机事件，在时间区间［t，t+Δt）内，故障概率与t 无关，而与区间长Δt 有关；装备在不相重叠的时间段内发生故障是相互独立的；在充分小的时间区间内最多只产生1 台故障装备。因此，可认定产生故障装备的数量服从Poisson 分布，即故障装备到达基本维修单元的间隔时间服从负指数分布。

2）排队规则。其主要是指基本维修单元对故障装备进行维修时采用的顺序。当故障装备数量小于基本维修单元数量时，即系统有空闲，基本维修单元立即对装备进行维修，且在同一时间内，每个基本维修单元只能对1 台故障装备进行维修；若故障装备数量大于基本维修单元数量，即系统无空闲，则故障装备进入排队系统等候。战时，到达排队系统的故障装备优先级往往相差不大，故在排队系统前等待维修的装备排队规则为先到先服务。

3）服务台。其由1 个基本维修单元构成。服务台完成维修所需的时间受装备类型、故障类型、维修的复杂程度等多种因素影响，很难确定服务时间的分布函数。为便于研究，文中假设完成故障装备维修的时间服从负指数分布。根据实际情况，基本维修单元的数量是有限的，且基本维修单元之间的维修过程是相互独立的。

4）系统容量。其主要是指排队系统能够接受的故障装备数量，本文假设该系统的容量是无穷的。

5）输出过程。指故障装备通过排队系统的维修后，各项性能指标满足作战要求，重新投入战场。

2.2 参数的获取

在本文中，服务台数量为待求参数，需要提前获得故障装备的到达速率和修复率作为已知条件。到达速率可通过对历次的演习数据统计分析获得装备的平均无故障工作时间MTBF，则到达速率为。修复率仍可由演习数据获得。统计某个时间段内某个基本维修单元处理的故障装备总量，以及处理这些故障所花费的总时间，前者除以后者即可得到平均修复率。

2.3 伴随保障的排队系统

伴随保障的排队系统是指配置于作战单元的基本维修单元对若干故障装备同时进行维修的系统。作战单元中装备数量是有限的，因此，属于顾客源有限模型。假设作战单元中的装备数量为m，基本维修单元数量为C（m＆gt;C），则伴随保障的排队系统可视为M/M/C/∞/m/FCFS 型排队系统。该系统的结构如图2 所示。

基本维修单元空闲概率为：

式中，n 为故障装备的数量。

有n 台装备故障的概率为：

当1≤n≤C 时，有：

当C+1≤n≤m 时，有：

故障装备的平均数量为：

排队等待维修的故障装备数量为：

战时，伴随保障主要是实施抢救抢修，要用尽可能少的时间恢复故障装备作战所需的功能，使之再次投入战斗。可用持续参战率，即某时段作战单元中满足作战要求的装备数量与所有装备数量的比值，来衡量该排队系统的维修效率。

持续参战率的计算公式为：

2.4 定点保障的排队系统

定点保障的排队系统是指在固定区域开设保障点，使用多个基本维修单元并行开展装备维修保障任务的系统。在战时定点保障中，通常基本维修单元集中配置在保障点中比分散配置工作效率更高，因此，本文只考虑基本维修单元集中配置的情况。顾客源是各个作战单元后送的故障装备，可认为故障装备数量是无限的。假设系统中有Z个基本维修单元独立并行服务，则定点维修的排队系统可视为M/M/Z/∞/∞/FCFS 型排队系统。维修单元的修复率为μ，故障装备到达速率为'，则系统的服务强度为：

当系统中的故障装备数量为n 时，基本维修单元空闲概率为：

排队等待维修的故障装备数量为：

战时，各作战单元将需要定点维修的装备送至指定地点，这就要求避免排队队伍过长造成拥堵，且战时装备维修对时效性要求较高，因此，可用故障装备在排队系统的等待维修时间，来衡量该排队系统的维修效率。

故障装备等待维修时间的计算公式为：

3 应用实例分析

假设某次作战任务中，在不同方向共配置了3个作战单元，装备维修保障使用伴随保障与定点保障相结合的方式，则伴随保障点数量S=3。每个作战单元中含有参战装备20 台。在伴随保障点中故障装备的到达速率是=4 台/h，定点保障点中故障装备的到达速率是'=6 台/h。基本维修单元中配置各专业维修人员共5 人，修复率是μ=10 台/h。求此次作战所需的装备维修保障人员数量。

根据式（3）～式（8），可计算出在每个伴随保障点中，不同数量的基本维修单元所对应的故障装备平均数量以及持续参战率，如表1 所示。

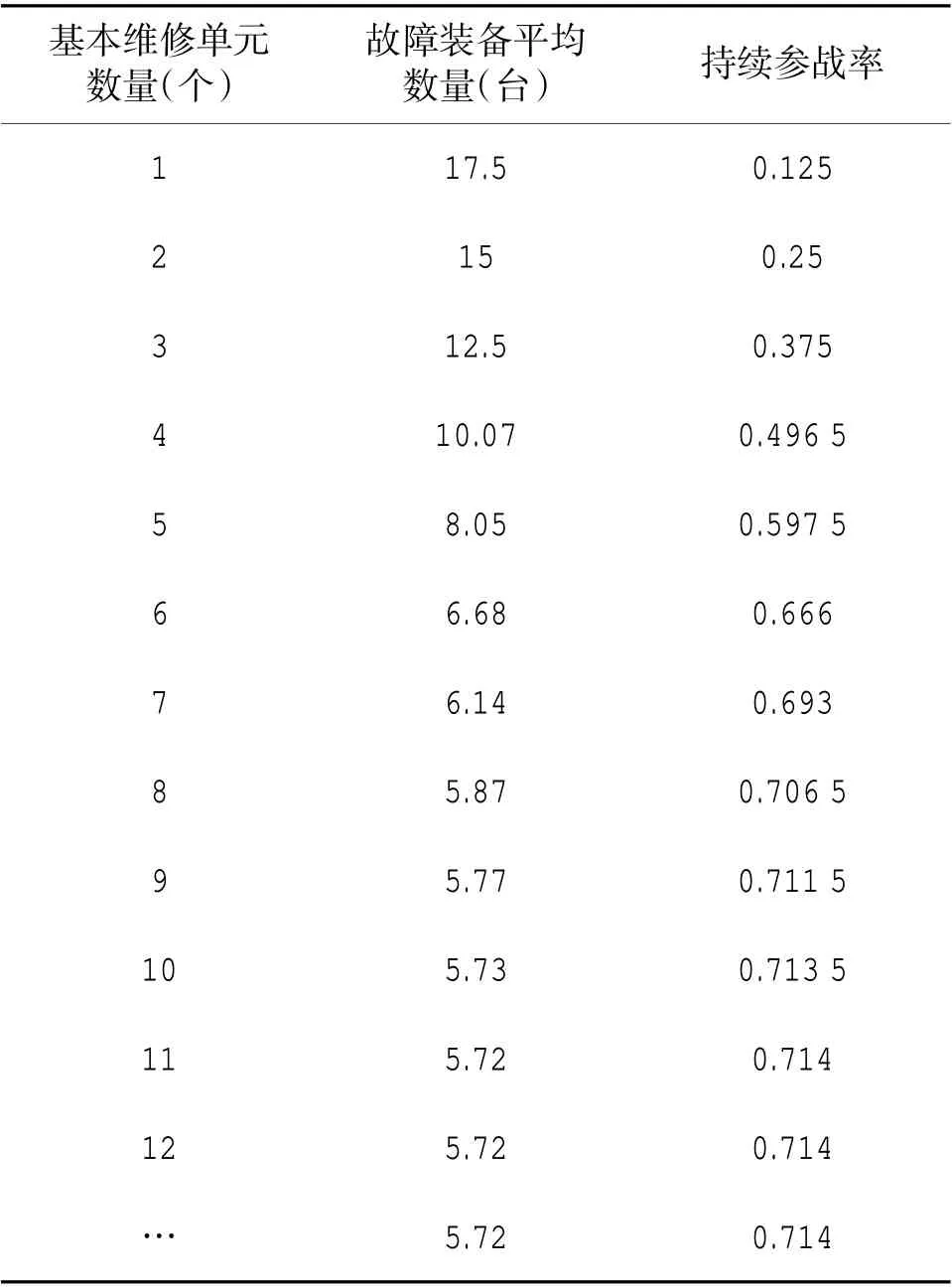
表1 持续参战率Table1 Continuous participation rate

由此得到基本维修单元数量与持续参战率的关系如图3 所示。

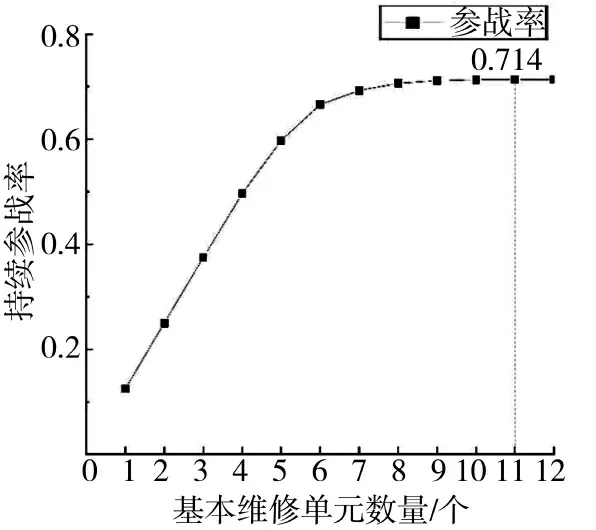
图3 基本维修单元数量与持续参战率的关系Fig.3 The relationship between the number of basic maintenance units and the rate of continuous engagement

从图中可以看出，随着基本维修单元数量的增加，装备的可持续参战率呈现先递增最后平稳的趋势，基本维修单元数量为11 个时，此时持续参战率达到最高，为71.4%。此时对应的故障装备平均数量根据实际情况取整后为6 台，当基本维修单元数量为7 个时，故障装备平均数量也为6 台，因此，可确定每个伴随保障点应配置7 个基本维修单元。共有3个伴随保障点，则需配置21 个基本维修单元，即伴随保障的维修人员共需21×5=105 人。

根据式（10）～式（13）可计算出在定点保障点中配置不同数量的基本维修单元时，故障装备的等待维修时间，如表2 所示。

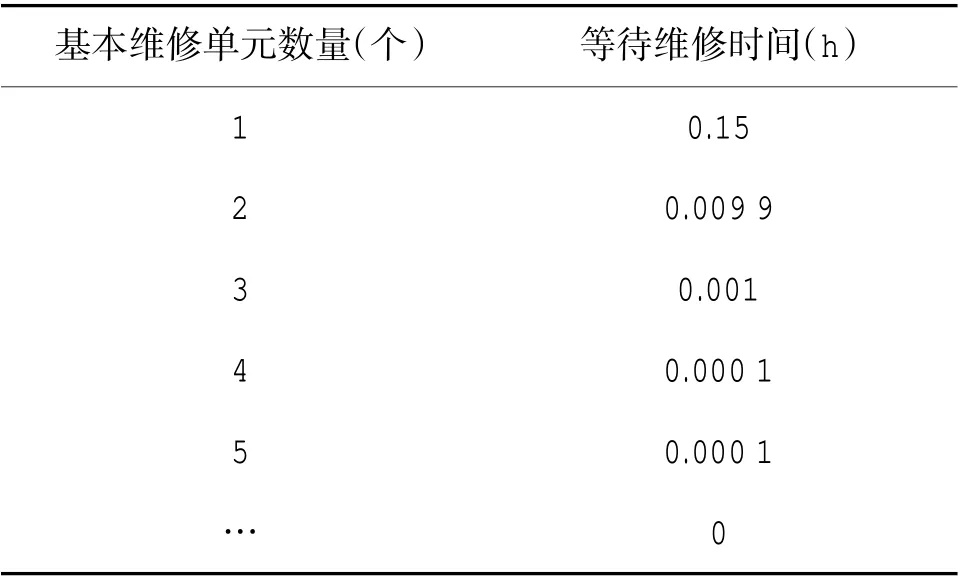
表2 等待维修时间Table 2 Waiting time for maintenance

由此得到基本维修单元数量与故障装备等待维修时间关系如图4 所示。

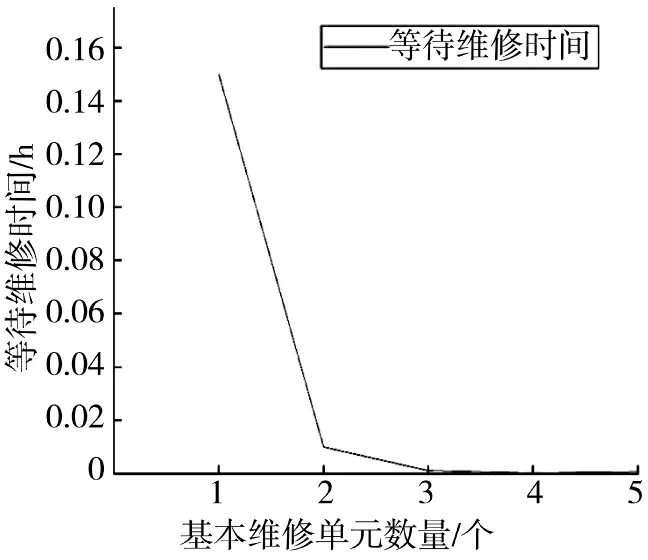
图4 基本维修单元数量与等待维修时间的关系Fig.4 The relationship between the number of basic maintenance units and waiting time for maintenance

由图可知，当基本维修单元数为2 时，等待维修时间迅速下降且趋近于0，之后再增加基本维修单元的数量，等待维修时间变化并不明显，只会造成资源浪费。说明当配置有2 个基本维修单元时，能保证故障装备的等待维修时间足够短，排队系统的工作效率也是最高的。因此，在定点保障中可配置2 个基本维修单元，即定点保障的维修人员共需2×5=10 人。

通过对伴随保障和定点保障所需维修人员的计算分析，最终得出此次作战所需的装备维修保障人员总数为105+10=115 人。

4 结论

本文以战时装备维修保障任务为核心，区分伴随保障和定点保障两种装备维修保障方式，运用排队论建立了这两种保障方式下的装备维修排队模型。通过实例分析，在战时确定装备维修保障人员数量时，只要由历史统计数据得到故障装备到达速率和基本维修单元的修复率，就可通过该模型计算出人员数量需求。该方法可为科学确定战时装备维修保障人员需求提供有效途径。