基于遗传模糊推理系统的截击点智能解算方法

李友江，汪亚斌

（信息系统工程重点实验室，南京 210007）

0 引言

空中截击是歼击机在领航员的引导下，对空中目标实施拦截与攻击的战斗活动。传统的截击引导采用人机结合，以人为主的方式，需要飞行员与领航员灵活运用飞机，才能达到较好的截击效果［1］。领航员根据当前的红蓝态势信息对截击点进行解算；最后利用截击点信息与歼击机当前状态解算出最短航路。由于传统截击引导需要人的参与才能完成截击任务，截击方案生成速度要受到人的反应速度的限制，成为提高作战速度的一个瓶颈。

针对上述问题，美军已经开展了大量智能化指控技术的研究，来应对快速、复杂、多变的未来战争，其中美国辛辛那提大学研制的阿尔法空战系统，成功战胜了人类资深飞行员，表现出了优异的作战性能，尤其在快速协调战术计划的速度方面是人类飞行员的250 倍［2-4］。如果传统的截击引导方式在未来战争中与美军阿尔法进行对抗，在决策速度上将表现出明显的劣势。因此，未来战争的新特征为截击引导带来了新的挑战，如何实现不需要人类参与的智能化引导控制器成为一个迫切需要解决的问题。对此，国内学者已有人开展相关研究，现有空战决策系统主要采用专家系统、基于对策和优化理论等方法求解［5-7］，计算相对最优解或局部最优解，但建模过程需要一定程度简化，使得结果难以符合实际情况。

模糊推理系统是基于模糊推理机制的系统，旨在模拟人脑处理概念的不确定性，为解决人类认知的主观性问题提供方法。模糊推理系统可以将客观数据与专家知识有效地整合，将自然语言的专家知识转换成数学模型或公式，保证逻辑推理过程的连续性和一致性［8-9］。并且可以提供高性能的控制，具有计算效率高、规则库及隶属函数易于定义和编码的优点。目前，各式各样的模糊推理系统已经成功应用在自动控制、自动驾驶、数据处理、决策分析及模式识别等领域［10-11］。

本文将模糊推理技术应用于截击引导领域，构建一种基于遗传模糊推理系统的截击点智能解算模型学习系统，并将遗传算法和模糊推理相结合，利用遗传算法对模糊推理系统的隶属函数和规则库进行优化训练。该方法能快速生成截击点相对于歼击机的距离、方位及截击时间，快速生成拦截方案，引导歼击机进行拦截，在模拟对抗系统中实现了可以替代人类领航员的空中作战智能引导控制器。

1 方法

基于遗传模糊推理系统的截击点智能解算方法关键技术有3 点，首先进行模糊推理系统的总体架构和算法流程设计，然后是态势信息处理和系统构建，最后是设计优化算法训练模糊推理系统。

1.1 算法流程和推理系统总体架构设计

本文提出的基于遗传模糊推理系统的截击点智能解算方法包括模型构建及训练，算法流程包括截击点智能解算模型构建，设计模糊推理系统的隶属函数与模糊规则库中规则，构建遗传算法基因字符串，利用遗传算法对模糊推理系统的智能模型进行训练，取出基因字符串数据库中适应度取值最小的个体，即为最优个体，对该个体的字符串代表的含义进行解析，得到模糊推理系统的结构特征参数，利用最优个体对应的特征参数构建模糊推理系统，即为要求解的截击点智能解算模型，算法流程如图1 所示。

图1 截击点解算智能模型训练流程图Fig.1 Flowchart of training the intelligent model for interception point calculation

模糊推理系统的输出包括截击点与歼击机相对距离、截击点相对于歼击机的方位、歼击机到达截击点的时间3 个输出，这3 个维度的信息共同描述了一种拦截方案，即某一时间到达某一具体截击位置。输入与输出之间由模糊推理引擎基于模糊规则库进行推理，结构图如下页图2 所示。

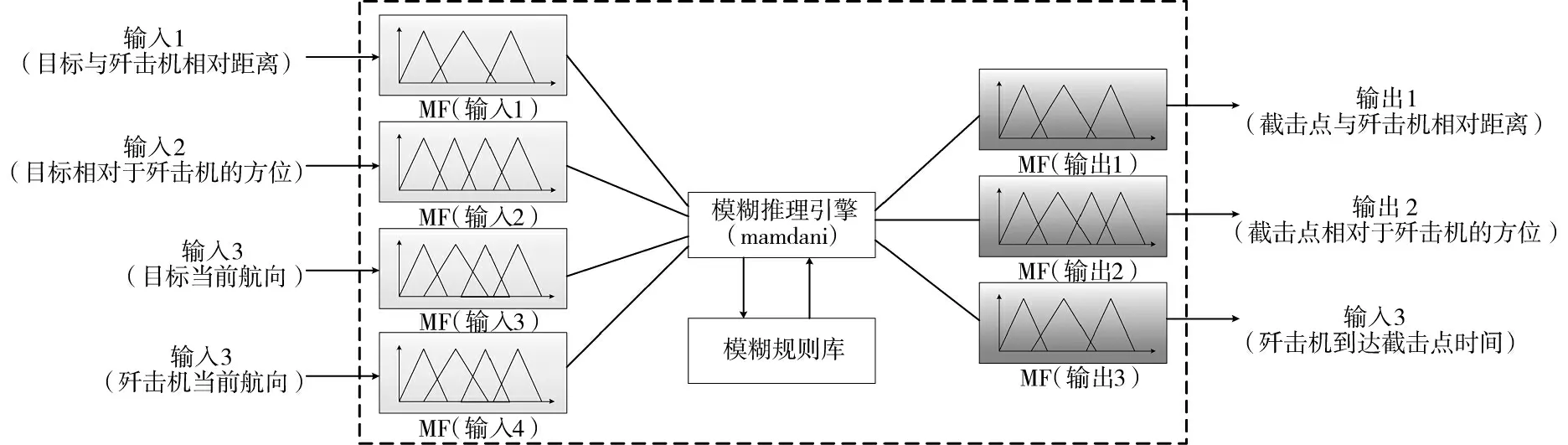
图2 截击点解算智能模型结构图Fig.2 The structure diagram of the intelligent model for interception point calculation

截击点智能解算模型进行模糊推理时，首先将态势信息转化成输入的4 个维度的精确值，并对精确值进行离散化和模糊化处理，得到每个维度的隶属等级和隶属度值，经过模糊推理引擎后得到输出的3 个维度的模糊化隶属等级和隶属度值，对每个维度的推理结果采用面积重心法去模糊化后，即可分别计算出精确的距离、方位和时间值，引导飞机进行拦截。

1.2 构建模糊推理系统

依次构建输入输出的模糊隶属函数。目标与歼击机相对距离由3 个三角形函数构成，从左到右依次代表目标距离歼击机的距离近、中、远；目标相对于歼击机方位的隶属函数由4 个三角形函数构成，从左到右依次代表目标位于歼击机的右上、左上、左下、右下；目标当前航向的隶属函数由4 个三角形函数构成，从左到右依次代表目标当前航向为左大、左小、右小、右大；歼击机当前航向的隶属函数由4 个三角形函数构成，从左到右依次代表歼击机当前航向为左大、左小、右小、右大。输入隶属函数如图3 所示。

图3 输入隶属函数Fig.3 Membership function of inputs

截击点与歼击机相对距离的隶属函数由3 个三角形函数构成，从左到右依次代表截击点与歼击机的距离近、中、远；截击点相对于歼击机的方位的隶属函数由4 个三角形函数构成，从左到右依次代表截击点位于歼击机的右上、左上、左下、右下；歼击机到达截击点时间的隶属函数由3 个三角形函数构成，从左到右依次代表截击时间为快、中、慢。输出隶属函数如图4 所示。

图4 输出隶属函数Fig.4 Membership function of outputs

模糊推理系统中模糊规则库包含3 个对应不同输出量的子模糊规则库，根据每个输出对应的输入量的个数及输入量隶属函数包含的三角形函数的个数，构造子模糊规则库中的规则个数均为3*4*4*4=192，模糊规则库中的总规则数为3*4*4*4*3=576。

隶属函数特征为输入输出量隶属函数中三角形函数的顶点横坐标位移量。基于模糊推理系统的截击点解算智能模型的输入输出隶属函数均由三角形函数构成，并且三角形函数的顶点的纵坐标分别为0、1、0。则每个三角形函数可以由3 个点唯一确定，即三角形3 个顶点的横坐标。为了对三角形函数的顶点进行一致描述，设定一个基准隶属函数，每个顶点用一位数来表示顶点的位移情况，其取值范围为1 到9 的整数，5 表示该点与基准隶属函数的横坐标一致，即不位移，1 到4 表示该点在基准隶属函数中对应点的基础上向左位移，6 到9 表示向右位移，位移的单位可以根据精度的需求设定，与5 差距越大代表位移越大。

模糊规则库特征为模糊规则库中规则的后置条件，该系统的模糊规则库中包含576 条模糊规则，每条规则由1 位数字来表示，每位的取值根据输出量对应的隶属函数中包含的三角形函数的个数，即求解截击点与歼击机相对距离的模糊规则对应位的取值范围为1、2、3，分别表示近、中、远；求解截击点相对于歼击机的方向的模糊规则对应位的取值范围为1、2、3、4，分别表示右上、左上、左下、右下；求解歼击机到达截击点时间的模糊规则库对应位的取值范围为1、2、3，分别表示快、中、慢。

在节能环保领域：坚持绿色发展理念，以环境评价和净化工程技术为核心，围绕生态环境监测与评估技术、工业“三废”综合治理技术、工/农业土壤修复与改良、工业过程环保技术、工业净化与节能环保材料等方向，积极拓展，联合开发，建设“生态环境工程技术中心”。

对模糊推理系统进行基因编码，每个个体的基因总长度为75+576=651 位，其中，前75 位对应模糊隶属函数，后面576 位对应模糊规则库。每个个体的基因都对应着一组模糊推理系统的参数，解析后都可以构建出唯一的一个模糊推理系统。

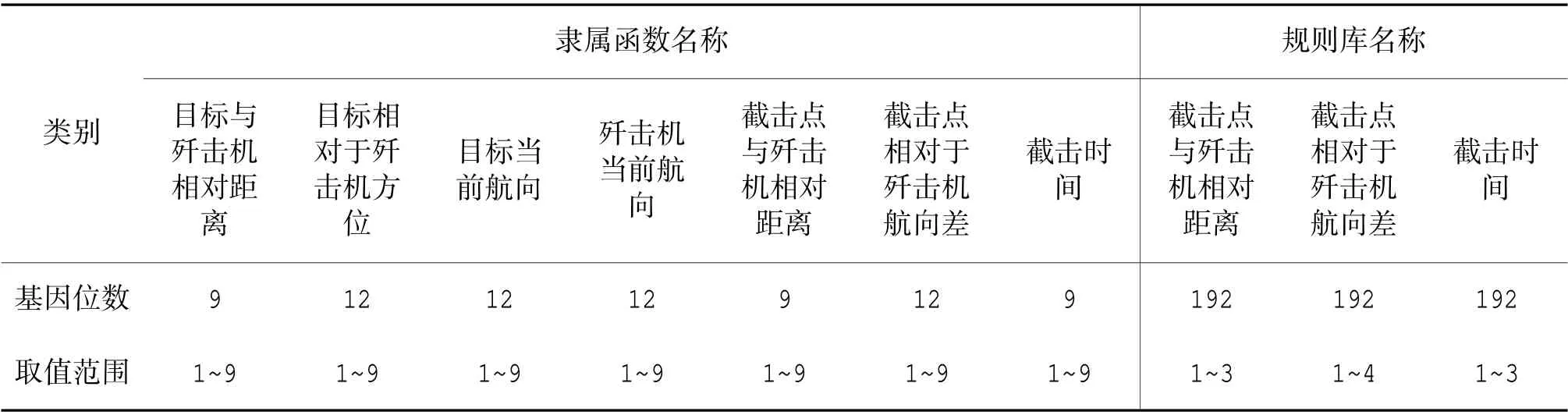
表1 隶属函数和模糊推理规则的基因编码长度和取值范围Table 1 Gene coding length and value range of membership function and fuzzy inference rules

1.3 分段变异和变步长寻优的遗传算法

该模糊推理系统可以在没有充足先验知识的情况下完成构建，经过学习训练后即可实现截击点的智能解算，由于没有充足的先验知识，模型参数初始化比较随机，利用传统标准的遗传算法学习训练时间长，收敛慢，且收敛后精度不高。经分析研究发现，由于描述隶属函数的基因位数与描述规则库的基因位数比例不均衡，本文中两者比例约为1∶8，如果对整个基因采用常规的变异操作会导致描述隶属函数部分的基因得到变异的概率很小，降低隶属函数得到优化的几率，延缓收敛速率，本文提出了一种分段变异和变步长寻优的改进遗传算法，其中分段变异是指每次进行变异操作时，对描述隶属函数的基因段和描述规则库的基因段分别进行变异，保证两段都能得到变异，同时可以设置不同的变异概率，有效控制两者的变异概率，变步长是指在训练初期，给隶属函数基因中一个移动单位设置较大的距离，扩大解的搜索范围，当训练趋于收敛时表示已经在较优解附近徘徊，然后逐渐降低隶属函数基因中一个移动单位代表的距离，从而逐渐探索到更优的解。

具体步骤如下：

Step 1：设所述种群数量为P，随机生成P 个基因字符串，构成初始种群，每个基因字符串称为一个个体，并且设置模糊隶属函数的初始寻优步长；

Step 3：保存种群中的全部个体及对应的适应度值，并记录本代中最优的适应度值；

Step 4：将适应度取值返回给遗传算法，利用适应度取值进行选择操作；

Step 5：从选择操作得到的剩余基因字符串中随机选择两个基因字符串分别进行交叉和变异操作，其中变异操作采用分段变异策略，设置分段变异概率，将基因字符串中表示模糊隶属函数的部分变异概率设为5%，将表示模糊规则的部分的变异概率设为8%。两种操作分别得到两个后代个体，循环进行交叉和变异操作过程，直到个体个数达到种群规模；

Step 6：判断最近10 次迭代中的最优适应度值是否得到改善，如果得到改善，跳到Step 2，否则，跳到Step 7；

Step 7：根据当前最优的适应度值对应的基因和基准隶属函数，计算出当前最优的隶属函数，并将其作为最新的基准隶属函数，将模糊隶属函数的寻优步长减半；

Step 8：循环进行Step 2～Step 7，直到循环次数等于最大迭代次数或训练效果达到预期取值。

图5 分段变异和变步长寻优的遗传算法流程图Fig.5 Flow chart of genetic algorithm for segmented mutation and variable step size optimization

2 算法实验

构建一对一的红蓝对抗仿真场景，对抗双方均采用传统引导算法，采集对抗数据，共进行500 局对抗，在每局中每隔10 s 采集一次态势数据，每组态势数据中包括红蓝双方飞机的坐标、速度、航向，以及传统引导算法给出的实时截击方案。然后进行数据预处理，将态势数据处理成模糊推理系统输入所需的4 个特征，并进行归一化。最后进行模型训练学习，训练结果如图6 所示。

图6 学习训练效果Fig.6 Learning and training effect

通过实验发现，常规的遗传算法需要迭代8 000 多代后收敛，采用分段变异和变步长寻优的方法后训练大约400 代就稳定收敛，训练收敛时间也由70 多个小时缩短到3 h 左右，且最终收敛后的最优质也有较大改善，常规训练收敛后取值大约0.272，而本文的方法收敛后取值约为0.197。

在图6（b）中可以看出采用分段变异和变步长寻优改进的遗传算法后，一方面适应度值可以快速下降，加快收敛速度；另一方面在每次变步长之后，适应度值能下降到比前一阶段更低的水平，表示模糊推理系统的智能解算准确度得到了进一步提高。从图6（c）可以看出，经过学习训练后模糊推理系统智能解算生成的截击点与传统引导算法给出的截击点基本一致，实现了截击点的智能解算。

最后，将训练得到的模糊推理系统在仿真对抗场景中与传统引导微分方程引导算法、基于时域滚动构建的专家系统、基于微分对策构建的空战智能体，以及基于混合优化算法的空战智能体分别进行100 局的对抗，对战统计结果如下页表2 所示。

从表2 可以看出，本文构建的模糊推理系统获胜率显著高于其他算法。表明利用遗传算法对模糊推理系统的结构特征进行寻优，最后得到在解空间内性能可以达到甚至超越人工的占位点解算智能模型。分析获胜原因如下：1）传统引导算法需要人工参与，包括选择战法类型、输入参数等人工操作，生成拦截方案耗时多，而对抗态势瞬息万变，经常错失战机，相反，模糊推理系统计算效率高，且不需要人工参与；2）基于传统数值计算的方法，对于一些临界点计算的拦截方案明显迂回过多，有时甚至会出现无解的情况，只能等待下一个决策周期重新计算，而模糊推理系统计算相对简单，在临界点、极端点等特殊态势下，也能给出相对合理的解，从而准确把握发弹机会；3）专家系统构建时难以覆盖所有可能场景，对战时易出现事先未知的态势，未能作出有效决策。

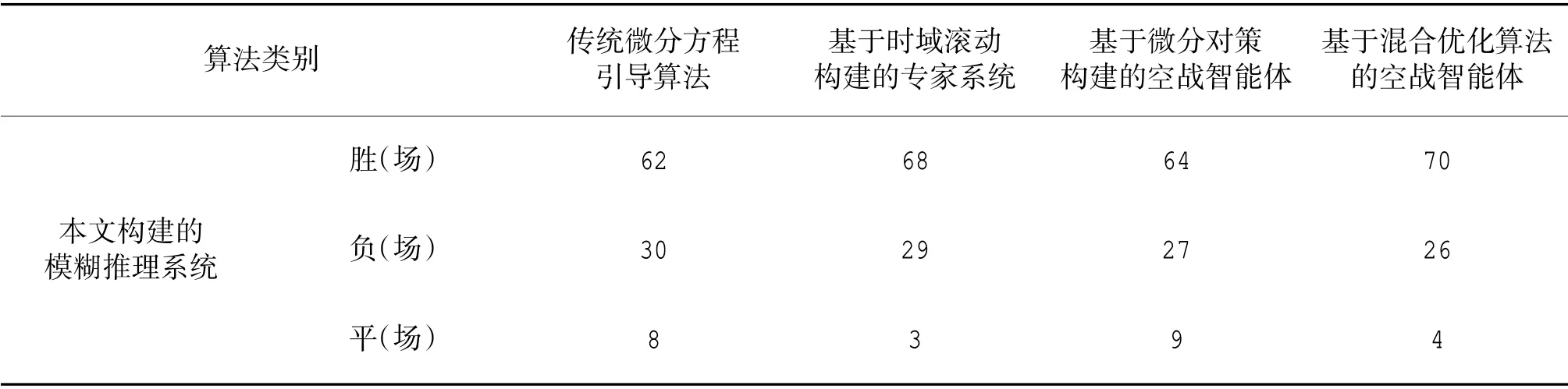
表2 不同算法构建的智能体之间的对战结果Table 2 Battle results between agents constructed by different algorithms

3 结论

本文的方法在缺乏充足先验知识的情况下，构建模糊推理系统，通过学习训练后实现了截击点的智能解算，在解空间内性能达到人类甚至超越人类的截击点解算智能模型，模型在解空间内具有普适性，对其进行调用之前不需要人为干预，实现真正无人化的作战飞机智能截击引导。