基于超效率平行网络DEA 的民用无人机岛礁运输效能评估方法研究

崔 栋，李宏伟，陆 鸣，曾杨智

（陆军工程大学野战工程学院，南京 210007）

0 引言

经典的无人机运输效能评估方法主要有专家经验方法[5]、数学解析方法[6]、模拟仿真方法[7]和机器学习方法[8]等。专家经验方法能够充分发挥专家的经验和知识优势，但存在主观判断偏差的局限；数学解析方法比较适用于简单明确的系统，当评估对象比较复杂时，模型公式的建立比较困难；模拟仿真方法是对现实场景的模拟，更加贴近应用背景，但是由于评估对象的复杂性和不确定性，许多因素不易量化，使得仿真试验存在“组合爆炸”问题；机器学习方法能够根据数据样本拟合效能评估模型，并作出合理的回归预测，但由于标记样本收集困难，模型训练易出现过拟合或欠拟合情况。而数据包络分析（data envelopment analysis，DEA）方法是适用于多输入、多产出系统的数据驱动型评估方法，能够有效克服情景模拟困难、主观判断存在偏差、标记样本缺乏等困难。DEA 模型把单输入、单输出的工程效率概念推广到多输入、多输出的同类型决策单元（decision making unit，DMU）的有效性评价中，其理论和方法在管理科学、经济评价、效能评估等领域广泛应用。在效能评估领域，冉景禄等[9]采用DEA 方法和风险评估模型相结合的方式，提出了旨在降低评估风险的装备效能稳健评估方法。吴坤鸿等[10]采用DEA 方法和逼近理想排序法相结合，在联合火力打击的目标选择和排序优化方面取得了较好的效果。以上研究主要是将DEA 作为一种数据处理方法，但对评估对象各评价指标的制约关系和内部结构缺乏描述。随着DEA 方法各种拓展模型的发展，网络DEA 模型已经成为当前的研究热点[11]，其在应用中可将评估对象内部结构关系纳入考量范围，得出更加精细的评价结果。周中良等[12]采用系统动力学与串行网络DEA 模型相结合的方法，能够基于评估对象的内部结构建立模型，其在突防兵力方案优选问题中取得了较好的效果。串行网络DEA 模型的典型特征是内部结构存在时序依赖关系，在应用中有其局限性。而对于内部结构相对独立、呈平行结构、没有前后依赖关系的评估对象，平行网络DEA 模型更加适用。

本研究在民用无人机岛礁运输效能评估中引入平行网络DEA 模型，首先把不同厂商型号的无人机作为决策单元，对无人机运输能力进行平行结构分解，将评价指标作为输入、输出变量。其次根据指标间生成关系，区分共享投入变量和独立投入变量，通过设置共享占比因子，调整共享投入变量在不同结构分项中的分配比例。最后引入超效率模型，将计算出的相对效率均值作为效能测度，评价结果比将评估对象作为“黑箱”的经典DEA 模型和一般平行网络DEA 模型更加精细，具有更好的适用性。

1 平行网络DEA 模型效能评估原理

1.1 平行网络DEA 模型

DEA 方法最早由Charnes、Cooper 和Rhodes 于1978 年提出，第一个DEA 模型（CCR 模型）就是以三人姓氏首字母命名[13]。基于规模收益不变（constant returns to scale，CRS）的CCR 模型和基于规模收益可变（variable returns to scale，VRS）的BCC 模型是DEA方法的最基本模型，也是超效率模型、非径向模型、广义DEA 模型等其他衍生模型的基础[13]。

经典DEA 模型对系统进行效能评估时，往往忽略了系统内部的运行结构，缺乏对系统内部约束关系的描述，其得出的评估结论往往不够全面。而网络DEA 模型作为打开决策单元“黑箱”的评估方法，由于建模过程考虑了系统内部的结构信息，更加符合系统运行实际，并且其评估结果能够揭示系统效能较低的原因，目前已广泛应用于银行[14]、交通[15]、运动[16]等领域的绩效评估。网络DEA 模型按照内部结构关系类型可分为串行、平行和混合结构模型[17]。平行网络DEA 模型结构示意图如图1 所示。

图1 平行网络DEA 模型结构示意图

在平行网络DEA 模型中，各决策单元内部的结构分项数量相同，各分项之间呈并行结构分布，并且相应的平行分项具有相同的投入和产出指标。系统总效率值计算公式如下：

1.2 评估思路和方法

应用平行网络DEA 模型进行装备选型，通常按照明确目标、效能评估和综合决策的操作流程。其中，明确目标是框定选型论证领域、待选型号和特征指标的思路引领；效能评估是采用合理方法对待选型号进行量化排序；综合决策是以效能评估结果为依据，综合多方面因素，最终选定拟用装备。效能评估可分为问题分解、建模计算和效能分析3 个阶段。问题分解阶段要确定待评估的对象（即决策单元），分析决策单元效能发挥的外部环境及影响效能目标的制约因素，分解决策单元内部结构，并确定各平行分项之间的关联关系。建模计算阶段要建立能够全面表征综合效能的指标体系，确定总体和分项结构的投入变量和产出变量，根据指标要求收集、整理数据，选取平行网络DEA 模型进行编程计算。效能分析阶段是根据计算得出的效率值，对决策单元的效能进行评估排序，并对结果进行分析和阐释。如果评估结果同实际情况有较大偏差，可返回内部结构分析和指标构建环节进行优化调整，直至最终得出能够合理解释的满意结果，以对最终做出决策提供技术支持。平行网络DEA 模型效能评估流程如图2 所示。

图2 平行网络DEA 模型效能评估流程

在评估民用无人机岛礁运输效能时，决策单元是不同厂商型号的无人机，评估目标是分析舰载民用无人机向偏离舰艇干线运输主航道的支线岛礁实施物资投送的运输效能。在此任务场景下，按照效能评估流程，采用平行网络DEA 模型进行效能评估，可实现对不同型号民用无人机岛礁运输的效能测度。

当今制造业同时面临着内部挑战和外部环境变化的双重压力。从企业内部看，用工成本越来越高、研发投入严重不足、生产组织方式较为传统都是目前亟待解决的具体问题。从外部环境看，消费者需求、技术变革、产业形态都在发生颠覆性的变化。

2 效能评估指标体系构建

民用无人机岛礁运输效能的指标体系与评估目的和背景相关，借鉴文献[18-19]中关于指标体系的构建方式，应对不同场景下民用无人机岛礁运输效能的评估，提出一种通用的指标体系架构，如图3 所示。在不同的运输投送场景和任务条件下，指标选取可在此基础上进行局部增删。

图3 民用无人机岛礁运输效能评估指标体系架构图

图3 是根据效能指标的层次结构构建的指标体系，在DEA 方法中，评价指标分为输入和输出模式。运输投送行动过程可以看作投入采购、维修、保养、支撑平台等成本，产出快速、准确、足量、安全、可靠的运输投送能力。在指标体系框架下，以民用同类型舰载无人机为决策单元，考虑运输环境为海上，根据此场景下的任务特点，将待评估的民用无人机运输能力分解为飞行平台基础能力和任务环境适应能力2 个平行分项，重点考量民用无人机运输投送和适应环境能力，评估模型结构如图4 所示。

图4 评估无人机岛礁运输效能的平行网络DEA 模型结构

由于投入、产出变量存在离散型数据、非量化数据等情况，为便于建模计算，针对采集数据现状，本研究在应用平行网络DEA 模型之前，对指标数据进行预处理，投入、产出变量量化表达方式详见表1。

表1 投入、产出变量量化表达方式

其中，抗盐雾能力、抗风雨能力、抗电磁干扰能力3 个指标采用试验数据和专家评价综合方式，按照1～10 标度方式表达，10 为性能最优，1 为性能最差。

3 效能分析与方法改进

民用无人机在消费级、专业级和行业级等不同层次都有着丰富的品类型号，其应用领域包括航拍、能源管道设备监测、农业植保、通信中继、应急响应、运输物流等[20]。其中，适用于军事领域岛礁运输的主要是运输物流、应急响应、农业植保等具备较强载荷能力的行业级无人机。本研究在民用行业级无人机中选取30 种不同型号的无人机型作为决策单元，重点参考大疆、迅蚁、亿航等不同品牌的旋翼和固定翼无人机型，按照表1 整理相应指标数据，得到的民用无人机投入、产出变量数据详见表2。

表2 民用无人机投入、产出变量数据

3.1 经典DEA 模型

首先采用CCR、BCC 模型，只考虑决策单元的投入、产出变量，不考虑内部分项结构关系，得到基于CRS 的综合效率、基于VRS 的纯技术效率以及规模收益类型，详见表3。

由表3 可知，在CRS 情况下，综合效率为1.000的决策单元数量为17 个；在VRS 情况下，纯技术效率为1.000 的决策单元数量更是达到26 个。由此可见，位于生产前沿面上的决策单元数量较多，效能的区分度较低，表明经典DEA 方法对相对（弱）有效决策单元之间的比较结果无法辨识。

表3 经典DEA 方法对民用无人机岛礁运输效能的评估结果

3.2 改进共享占比的平行网络DEA 模型

采用平行网络DEA 模型，虽然系统总效率唯一确定，但是得到的DMU0最优解可能不唯一，因此在进行分项效率分解时存在分项效率值不唯一的情况。借鉴雷西洋[21]采用的方法，在保持总系统效率最优的条件下，将第p0个分项单元最优效率按照以下公式计算，以效率区间的方式表示平行分项的效率值：

式中，θ1*是公式（1）中目标函数的最优值，第4 个约束确保总系统效率不变；Max θ1*和Min θ1*分别表示分项效率的最大值和最小值，因此分项效率值位于区间[Min θ1*，Max θ1*]，如果Max θ1*=Min θ1*，则平行分项p的效率值唯一确定。根据图4 的平行网络DEA 模型结构，由于存在共享投入指标，增加共享占比参数α和β 后，原模型不再是线性规划，为考察不同共享占比对效率值的影响，在计算过程中，设α=k1ε、β=k2ε，其中ε 为人为设定的步长，表示计算精度，k1、k2∈[1，1/ε-1]且k1、k2∈N*，对迭代计算得到的效率矩阵取算数平均值作为最终的效率值。

根据构建的平行网络DEA 模型，综合考虑运算耗时和结果精度，通过多次试验发现，步长ε 取值为0.01～0.10 相对合适。假定步长ε 的值为0.05，按照公式（1）对30 种不同型号民用无人机进行效能评估，将每次迭代得到的效率值绘制成网格图，如图5 所示。

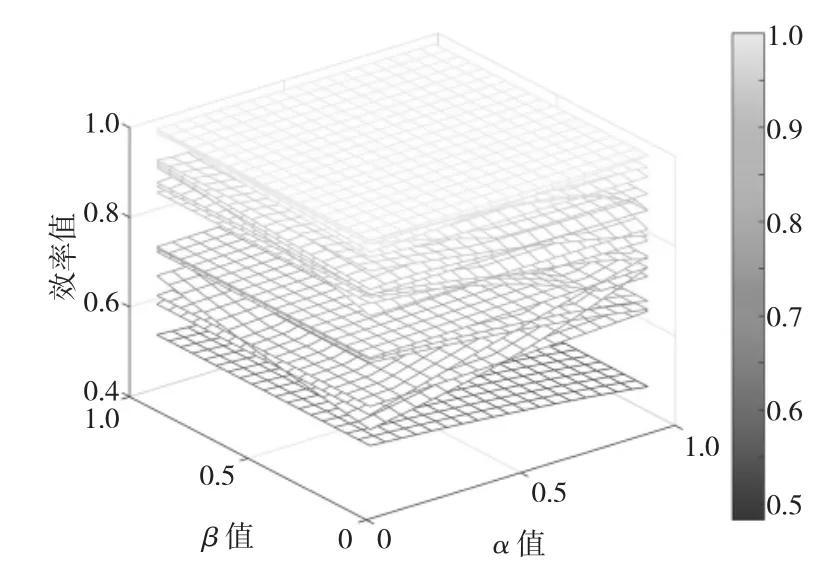
图5 DMU 系统总效率网格图

根据公式（2），对DMU 系统总效率进行分解，得出基础能力效率最小值、最大值和适应能力效率最小值、最大值，其对应网格图如图6～9 所示。

图6 DMU 基础能力效率最小值网格图

图7 DMU 基础能力效率最大值网格图

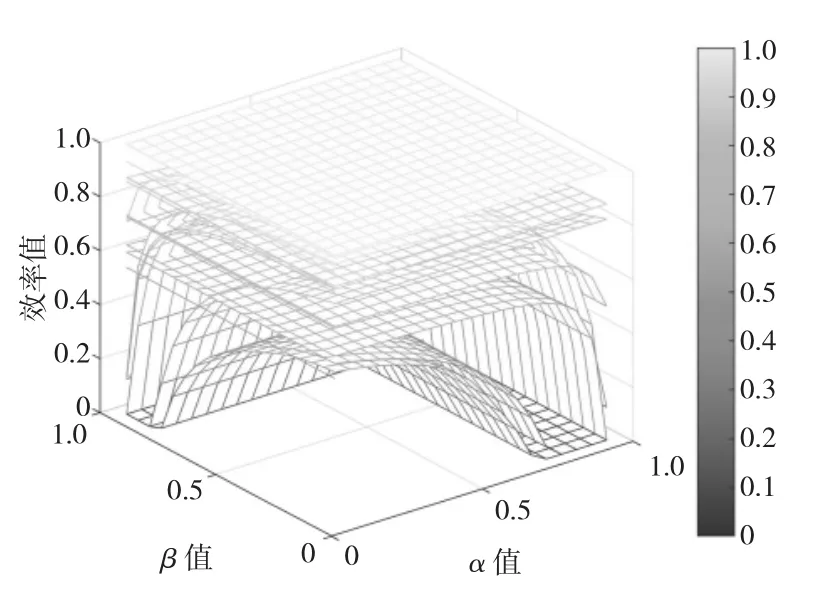
图8 DMU 适应能力效率最小值网格图

图9 DMU 适应能力效率最大值网格图

3.3 进一步引入超效率平行网络DEA 模型

对比经典DEA 模型，采用平行网络DEA 模型可以明显减少效率值为1.000 的民用无人机数量，同时具备进一步解析平台基础效能和环境适应效能的优势。然而由于模型中投入、产出指标数量相对较多，仍然存在一定数量效率值为1.000 的决策单元无法精细分辨。为实现所有待评估民用无人机的全排序，在平行网络DEA 模型的基础上，引入超效率DEA，将被评价决策单元从参考集中剔除，即总约束和平行分项约束条件中减少对决策单元自身的约束，构建超效率平行网络DEA 模型，从而实现对有效决策单元的进一步区分。其计算方法如下：

在进行民用无人机岛礁运输效能评估时，综合考虑平行网络DEA 模型的总效率、平行分项效率和超效率，可以得出相对全面的评估结果。在超效率平行网络DEA 模型中，同样假定步长ε 为0.05，按照公式（3）建模计算，得到总效率网格图如图10 所示。

图10 超效率平行网络DEA 模型DMU 系统总效率网格图

3.4 不同模型对比分析

为便于对比不同模型的测度结果，依次对经典CCR 模型、平行网络DEA 模型（包括总效率和平行分项效率）、超效率平行网络DEA 模型编程计算结果取算数平均值（即网格图中一个平面所有取值的算数平均值），得出不同模型对民用无人机岛礁运输效能的评估结果，详见表4。

从表4 可知，飞行平台基础能力分项效能的最小值和最大值相等，对应图6 和图7 中网格图也相同，表明基础能力分项效能值能够唯一确定。在任务能力分项效能值中，有11 个决策单元最小值和最大值不同，说明满足系统总效率值的前提下，最优解不唯一，此时分项效能值是介于最大值和最小值之间的区间数。DMU14、DMU15、DMU30任务环境效能分项无最优解，说明系统总效能值最优解无法满足任务环境分项中的约束条件，这也是下一步模型需要改进的地方。

表4 民用无人机岛礁运输效能评估结果

采用经典CCR 模型评估，共17 个决策单元为DEA 弱有效。按照平行网络DEA 模型评估，有效的决策单元单元数量减少至10 个，由于引入了系统内部结构关系约束，因此对决策单元的区分更加精细。在此基础上，进一步引入超效率平行网络DEA 模型，可以实现包含内部结构信息的全排序，评估结果的区分度更加明显。效能分析说明DMU30、DMU2、DMU16排在前三位，可作为重点考虑的民用无人机型号。

通过分析平行分项单元效率，可以进一步得出总效率较低的原因。这是由于系统总效能值介于各平行分项单元效能值之间，可以为系统改进方向提供参考，即设法提高效能值较低的分项单元。例如DMU23总效率为0.886、基础能力分项为0.929、任务能力分项区间为[0.537，0.823]，可以看出是由于任务能力分项较低导致了总效率值偏低。

4 结语

为了对民用无人机岛礁应急物资运输装备军选决策提供技术参考，本研究采用平行网络DEA 模型进行效能测度，通过考量决策单元内部结构信息，改进平行分项共享占比，引入超效率DEA，构建了改进共享占比的超效率平行网络DEA 模型，实现了参评民用无人机的全排序，有助于适用机型优选参考。对比分析结果表明，改进后的模型相较经典CCR 模型和平行网络DEA 模型，效能评价结果的辨识度更加清晰、区分度更好、解释性更强，在具有内部平行结构的效能评估问题中具有较高的应用价值。但由于增加了内部平行分项约束条件，在有些共享占比的情况下存在没有最优解的问题，需要在后期研究中进一步完善和改进。