基于神经网络的超声背散射零差K 成像脂肪肝评价方法研究

丁琪瑛，吴水才，崔博翔，周著黄*

（1.北京工业大学校医院超声室，北京 100124；2.北京工业大学环境与生命学部，智能化生理测量与临床转化北京市国际科研合作基地，北京 100124；3.台湾长庚大学医学院，台湾桃园33302）

0 引言

肝脏脂肪变性是一种因肝细胞内沉积过多脂肪导致的慢性肝病，同时是非酒精性脂肪性肝病（nonalcoholic fatty liver disease，NAFLD）的主要表现。全球人群中，NAFLD 的患病率高达25%[1]，而我国流行性NAFLD 的总病例数约为2.43 亿[2]，且有低龄化趋势。据估计，约有20%的NAFLD 可能进展为脂肪性肝炎（nonalcoholic steatohepatitis，NASH），其中又有约20%的NASH 可能进展为肝硬化和肝细胞癌[3]，因此脂肪肝的早期诊断和跟踪监测具有重要意义。

临床上，肝穿刺活检仍是诊断脂肪肝的金标准，但其具有侵入性，且可能导致取样误差、诱发并发症等问题，并不适合脂肪肝的筛查和监测。因此，非侵入性的医学影像学方法广受关注。相比CT 和MRI，超声成像设备具有价格低廉、易获取、实时性好、可移动性佳等优势，被广泛用于肝病的检查，但临床最常用的B 超成像是一种非定量成像方式，且对早期脂肪肝的检测敏感度较低[4]。因此，近年来定量超声技术受到了较多关注，定量超声参量主要包括声速、声衰减、功率谱参数、背散射统计（包络统计）、弹性等声参量[5-8]。定量超声可通过分析原始超声背散射信号，提取与生物组织微结构或状态直接相关的声参量。

声学上，肝脏组织可建模为一系列散射声波微小粒子即散射子的组合[9-10]。对于正常肝脏，肝细胞和肝小叶等是肝脏的超声散射子，而当肝脏发生脂肪变性时，脂肪滴成为额外的散射子。这种肝脏微结构或状态的改变，最终体现在从散射子接收的背散射回波信号中。超声背散射信号的包络统计可兼容传统超声成像架构，使其成为一类重要的定量超声参量。超声背散射零差K 模型是参数最具物理意义的包络统计模型[11]，其参数估计方法主要有信噪比-偏度-峰度（signal-to-noise-ratio，skewness，kurtosis，RSK）法[12]和X 统计-U 统计（X-statistics，U-statistics，XU）法[13]。虽然RSK 法和XU 法在基于超声背散射零差K模型的组织定征中大量应用，但这2 种方法均存在计算复杂度较高的问题。而神经网络法可以直接将特征参数输入至训练好的神经网络模型中，即可得到参数估计，因此计算复杂度明显低于传统RSK 法和XU 法。

本研究提出基于神经网络估计零差K 模型参数的方法，并在此基础上提出基于神经网络的超声背散射零差K 成像评价脂肪肝的新方法。

1 方法

1.1 理论基础

1.1.1 超声背散射零差K 模型

对于超声背散射信号包络振幅A，零差K 分布模型的概率密度函数f（·）定义为[11]

式中，α 表示散射子聚集参数，理论上可反映超声分辨单元内的有效散射子个数；ε2和2σ2α 分别表示相干散射信号和弥漫散射信号的能量；J0（·）表示零阶第一类贝塞尔函数；x 表示积分变量。根据ε 和σ，可以推导出表示相干散射信号与弥漫散射信号比值的k 参数，其计算公式如下：

理论上，k 参数可以反映散射子分布的周期性或准周期性。

1.1.2 超声背散射零差K 模型参数的传统估计方法

超声背散射零差K 模型参数的传统估计方法主要包括RSK 法[12]和XU 法[13]。以Av表示包络振幅A的v 次幂，RSK 法的基础是Av的信噪比R、偏度S和峰度K，其计算公式分别如下[12]：

式中，E[·]表示数学期望。

RSK 法首先通过蒙特卡罗仿真，计算不同α 和k 的参数组合下R、S、K 的理论值。在实际估算时，根据背散射信号包络计算R、S、K 的实际值，再将实际值与理论值放在二维参数空间里进行比对，搜寻最佳水平曲线对应的α 和k 参数值，即为参数估计。Hruska 等[12]研究发现，RSK 法最优的v 次幂为v∈{0.72，0.88}。

XU 法主要基于包络信号强度I（I=A2）的X 统计和U 统计，X 和U 的计算公式分别如下[13]：

XU 法通过在E[I]=Iˉ（Iˉ为平均强度）、XHK=X（XHK和X 分别为X 的理论值和测量值）、α≤αmax这些约束条件下，求解以下非线性方程得到α 和k 的参数估计[13]：

式中，UHK和U 分别为U 的测量值和理论值；arg min（·）是指括号内条件满足最小值时对应公式（8）等式左端的参量值。在通过公式（8）计算出α、ε2和σ2参数之后，可根据公式（2）计算出k 参数的值。

1.2 基于神经网络的超声背散射零差K 模型参数的估计方法

通过理论分析和试验发现，传统RSK 法的水平曲线空间搜寻和XU 法的非线性方程求解均存在算法计算复杂度较高的问题，且RSK 法存在搜寻不到最优解而导致无效估计的情况。为此，本研究在前期工作的基础上[14]，提出了改进的神经网络估计超声背散射零差K 模型参数的方法，其算法流程如图1所示。图1 中，左侧为神经网络训练流程图，训练得到神经网络模型；右侧为神经网络测试流程图，先利用蒙特卡罗仿真得到模拟的超声背散射包络信号样本，或临床超声背散射信号经包络检测得到包络信号，然后提取特征参数输入到训练好的神经网络模型中，即可得到lg α 和k 参数估计。由于本研究提出的神经网络法可以直接将特征参数输入神经网络模型得到参数估计，因此计算复杂度明显低于传统RSK法和XU 法。

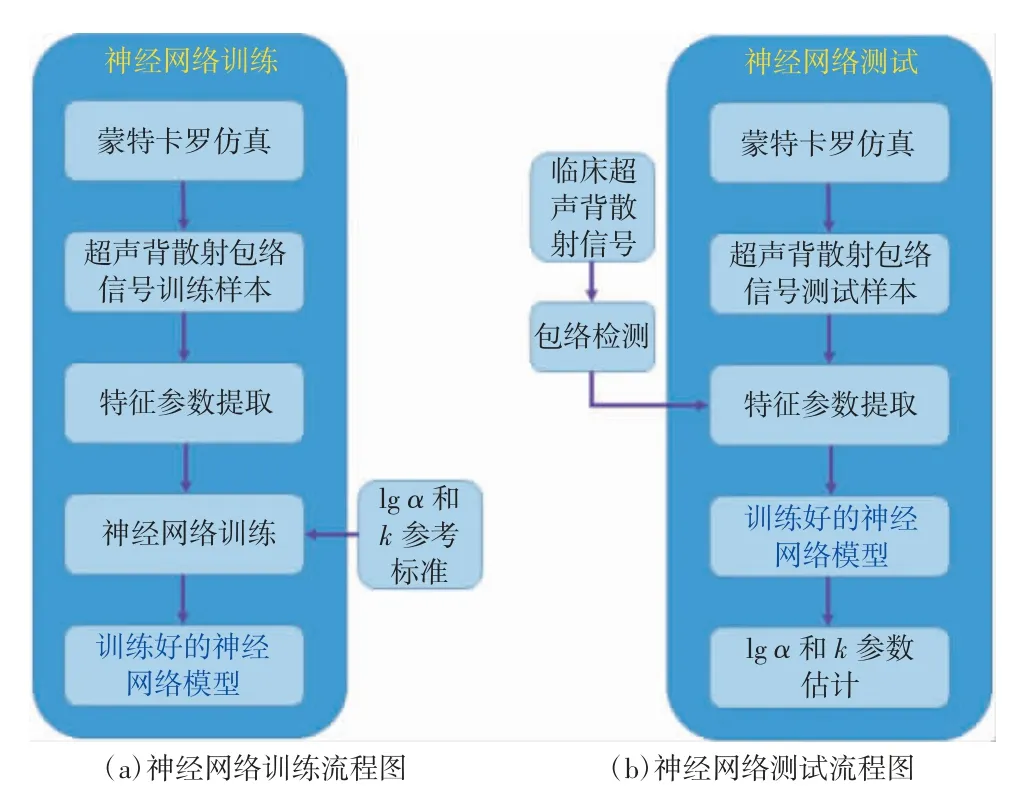
图1 基于神经网络的超声背散射零差K 模型参数估计算法流程图

1.2.1 蒙特卡罗仿真产生神经网络训练样本

利用蒙特卡罗仿真产生包络信号训练样本，这些训练样本服从零差K 分布、独立同分布（independent identically distributed，IID），且对应于不同lg α 和k 参数的组合：lg α∈{-1.00，-0.99，…，-0.01，0.00，0.01，…，1.99，2.00}、k∈{0.00，0.01，…，1.99，2.00}。在训练神经网络模型时，以上各数值分别是不同组合下lg α 和k 参数的参考标准。因此，共产生301×201=60 501 组训练样本。每个训练样本的包络信号长度为216（即216 个数据点）。对于任意一组lg α 和k参数，蒙特卡罗仿真产生服从零差K 分布的IID 包络信号样本TS 的计算公式如下[14]：

式中，X 和Y 是服从单位高斯分布的IID 包络信号样本；z 是服从伽马分布的IID 包络信号样本，伽马分布的形状参数为α、尺度参数为1。

1.2.2 输入神经网络的特征参数

根据超声背散射包络信号估算零差K 模型参数，是一个逆问题。由于RSK 法的3 个参数R、S、K 和XU 法的2 个参数X、U 都可以用于估算零差K 模型参数，因此，本研究基于神经网络模型提出一种方法可以综合运用这些参数，并且能够避免传统RSK 法和XU 法计算复杂度较高的问题。通过设置神经网络的特征参数、网络结构和训练方式，可以有效地提高其估算性能。

本研究考虑以下15 个特征参数：公式（3）～（5）中，设置v∈{0.72，0.88，2.00}，共得到9 个与R、S、K对应的特征参数；公式（6）～（7）中，用I1=Av替代原本的I=A2，同样设置v∈{0.72，0.88，2.00}，如此可得到6 个与X、U 对应的特征参数。

1.2.3 神经网络结构

神经网络结构如图2 所示的前馈神经网络，由1 个输入层、2 个隐含层和1 个输出层构成。输入层共有15 个神经元，对应于上文所述的15 个特征参数；隐含层1 和隐含层2 的神经元个数分别为40和15；输出层有2 个神经元，分别对应于lg α 和k参数值。

图2 前馈神经网络结构示意图

1.2.4 神经网络模型训练

采用误差反向传播（back propagation，BP）算法训练前馈神经网络，具体为Levenberg-Marquardt BP算法[15]。在训练神经网络之前，将训练样本和参考标准的值映射到[-1，1]范围，以加速训练。在神经网络测试时，再将网络输出值反映射到原来的范围。学习率设置为0.01，损失函数为均方误差。2 个隐含层的传递函数为双曲正切S 形（即Sigmoid）传递函数，输出层为线性传递函数。

1.3 基于神经网络的超声背散射零差K 成像方法

基于神经网络的超声背散射零差K 成像方法流程图如图3 所示。超声背散射零差K 成像是基于α 和k 参数的映射图，通过在包络信号上使用滑动窗口处理得到。主要步骤包括：（1）在包络信号上，使用一个正方形窗口以获取局部背散射信号，这些信号数据输入训练好的神经网络模型，得到α 和k 参数估计值，再将这些估计值赋予位于窗口中心的新像素；（2）正方形窗口以一定的步长即窗口重叠率在包络信号上滑动，重复此步骤以产生α 和k 参数图；（3）利用扫描变换将α 和k 参数图转换为凸阵图像，并使用伪彩色映射以便显示，再设置肝实质感兴趣区域（region of interest，ROI）；（4）将ROI 内的α 和k 图像叠加显示到B 超图像上，同时显示结构信息和参数信息，即基于神经网络的超声背散射零差K 成像。为了在抑制边界伪影的同时提高成像分辨力[16]，本研究使用换能器脉冲长度的1 倍作为窗口边长，以实现小窗口超声背散射零差K 成像。

图3 基于神经网络的超声背散射零差K 成像方法流程图

1.4 试验数据

1.4.1 计算机仿真实验数据

利用公式（9）的蒙特卡罗仿真产生测试样本，以评估各参数估计方法的性能。这些服从零差K 分布的IID 测试样本，对应于不同的lg α 和k 参数组合：lg α∈{-1.0，-0.9，…，-0.1，0.0，0.1，…，1.9，2.0}；k∈{0.0，0.1，…，1.9，2.0}。在测试神经网络模型时，以上各数值分别是不同组合下lg α 和k 参数的参考标准。因此，共产生31×21=651 组测试样本。每个测试样本的包络信号长度同样为216。对于每组测试样本，重复试验100 次。

利用以下指标评价估算性能[14]：相对均方根误差（relative root mean square error，RRMSE）、相对偏差（relative bias，RB）、归一化标准差（normalized standard deviation，NSD），具体计算公式如下：

1.4.2 临床试验数据

临床试验数据经批准在台湾长庚医院采集[17]，所有受试者均签署了知情同意书。受试者分为2 组：第一组为72 名肝脏捐献者，第二组为204 名慢性乙肝患者。第一组男女比例为24∶48，平均年龄为（38.2±13.3）岁；第二组男女比例为148∶56，平均年龄为（54.7±12.4）岁。第一组受试者脂肪肝检测的参考标准为磁共振波谱（magnetic resonance spectroscopy，MRS）测量的肝脏脂肪分数（hepatic fat fraction，HFF）。第二组受试者脂肪肝检测的参考标准为肝穿刺活检，根据组织学检查结果将脂肪肝程度分为4 个等级：正常（S0）（肝脏脂肪变性<肝细胞数量的5%）；轻度（S1）（肝细胞数量的5%≤肝脏脂肪变性<肝细胞数量的33%）；中度（S2）（肝细胞数量的33%≤肝脏脂肪变性<肝细胞数量的66%）；重度（S3）（肝脏脂肪变性≥肝细胞数量的66%）

在行MRS 或组织学检查之前，受试者均进行了标准的腹部超声检查，超声扫描仪为Terason 3000型（Terason，Burlington，MA，USA），凸阵换能器（5C2A型，Terason）的中心频率为3 MHz，阵元数为128，脉冲长度（pulse length，PL）约为2.3 mm。超声成像的焦点和深度分别为4 cm 和8 cm。原始超声背散射信号由128 条扫描线组成，采样频率为30 MHz。利用MATLAB 软件（R2020a，MathWorks，Natick，MA，USA）进行背散射信号的离线处理。

1.5 临床超声背散射信号处理

对临床超声背散射信号进行希尔伯特变换，以获取包络信号。对包络信号进行对数压缩（动态范围40 dB），并进行扫描变换，以构建B 超图像。采用未压缩的包络信号进行超声背散射零差K 成像。将滑动窗口的边长设置为1PL，以保证零差K 成像有较高的分辨力。为了在成像分辨力和计算时间之间进行折中，将滑动窗口的重叠率设置为50%[16]。通过在B超图像上手动勾画ROI 以获得定量测量，再将ROI应用于相应的零差K 图像，计算出ROI 内图像像素值的平均值。

1.6 统计学分析

对于第一组受试者，计算Pearson 相关系数r 和概率P，以评估超声背散射零差K 模型参数与HFF之间的相关性（P<0.05 表示差异具有统计学意义）。对于第二组受试者，使用95%置信区间（confidence interval，CI）分析受试者ROC，计算≥S1、≥S2、≥S3的AUC 值（≥S1 表示S0 与S1～S3 的二分类，≥S2表示S0～S1 与S2～S3 的二分类，≥S3 表示S0～S2 与S3的二分类），以评估诊断不同程度脂肪肝的性能。利用SigmaPlot 软件（v12.5，Systat Software，CA，USA）进行统计分析。

2 结果

2.1 计算机仿真试验结果

不同估计方法估算超声背散射零差K 模型lg α 和k 参数性能的对比结果详见表1～2。RRMSE、RB、NSD 的数值越小，代表估算性能越好。在RRMSE和NSD 方面，本研究提出的神经网络法均优于传统RSK 法和XU 法。在RB 方面，对于lg α 参数，本研究提出的神经网络法略差于传统的RSK 法和XU 法。而对于k 参数，本研究提出的神经网络法优于RSK法。整体上来看，本研究提出的神经网络法优于传统RSK 法和XU 法。

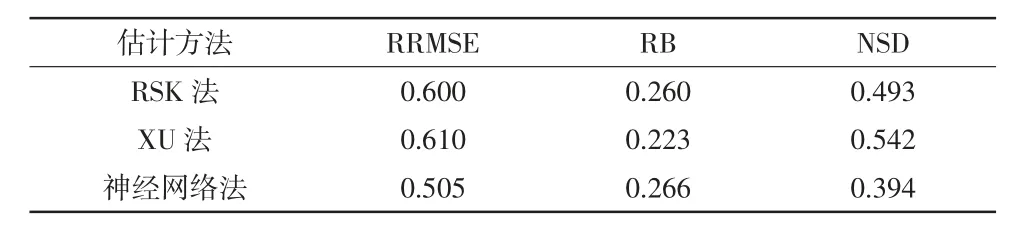
表1 不同估计方法估算超声背散射零差K 模型lg α 参数的精度对比结果

表2 不同估计方法估算超声背散射零差K 模型k 参数的精度对比结果

在运行效率方面，利用普通计算机在MATLAB 环境下测试算法的平均运行时间，结果如下：RSK 法为0.164 6 s，XU 法为0.102 1 s，本研究提出的神经网络法为0.011 3 s。可见，神经网络法的运行效率明显高于RSK 法和XU 法。

2.2 临床试验结果

2.2.1 第一组受试者的临床试验结果

不同程度脂肪肝的B 超成像与基于神经网络的超声背散射零差K 模型αNN和kNN成像如图4、5 所示。αNN和kNN图像中每一个像素值对应于色阶条中αNN和kNN的数值，因此是一种具有物理意义的定量超声成像方式。相比之下，B 超图像的像素值对应于对数压缩之后的灰阶，是以相对方式显示组织回波信号的幅度或回波反射性，且B 超图像的灰阶会受动态范围、图像后处理等参数的影响，所以B 超图像是一种非定量即定性的成像方式。由图4 和图5 可见，随着脂肪肝严重程度的增加，超声背散射零差K模型αNN和kNN图像的整体亮度逐渐增大，表明αNN和kNN成像能够以可视化方式直观地定征或评价脂肪肝。

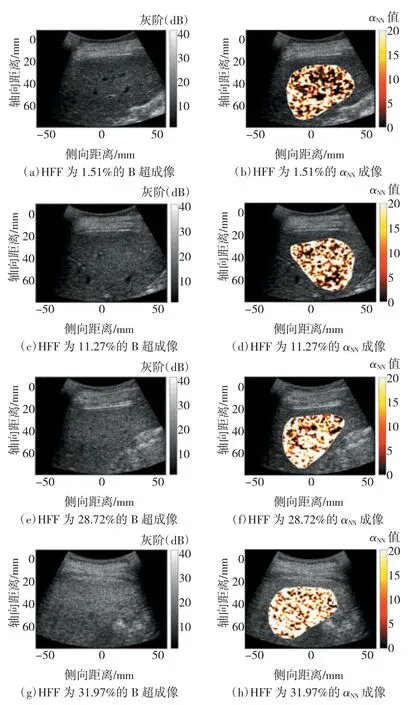
图4 不同程度脂肪肝的B 超成像与基于神经网络估计的超声背散射零差K 模型αNN 成像

图5 不同程度脂肪肝的B 超成像与基于神经网络估计的超声背散射零差K 模型kNN 成像

Zhou 等[16]研究发现超声背散射统计参数与HFF非线性相关，但与lg HFF 呈线性相关。因此，本研究分析超声背散射零差K 模型参数与lg HFF 的相关性，基于神经网络估计的αNN和kNN参数与lg HFF 的散点图与线性拟合分别如图6、7 所示，相关系数分别为r=0.651（P<0.000 1）和r=0.650（P<0.000 1），表明αNN和kNN参数与lg HFF 均有较好的线性相关性。

图6 基于神经网络估计的超声背散射零差K 模型αNN 参数值与lg HFF 的散点图与线性拟合

利用传统RSK 法和XU 法估计的超声背散射零差K 模型αRSK和αXU参数与lg HFF 的相关性分别为r=0.094（P<0.000 1）和r=0.628（P<0.000 1）。相比于传统RSK 法和XU 法，本研究提出的基于神经网络估计的超声背散射零差K 模型参数与lg HFF 之间具有更好的相关性。

2.2.2 第二组受试者的临床试验结果

肝活检结果表明，不同程度脂肪肝的受试者例数分别为80 例（S0）、70 例（S1）、36 例（S2）、18 例（S3）。基于神经网络估计的超声背散射零差K 模型αNN和kNN参数与脂肪肝程度的箱形图分别如图8、9 所示，随着脂肪肝严重程度的增加，αNN和kNN参数值均呈现增大趋势，表明αNN和kNN参数能够检测不同程度的脂肪肝。

图7 基于神经网络估计的超声背散射零差K 模型kNN 参数值与lg HFF 的散点图与线性拟合

图8 基于神经网络估计的超声背散射零差K 模型αNN 参数值与脂肪肝程度的箱形图

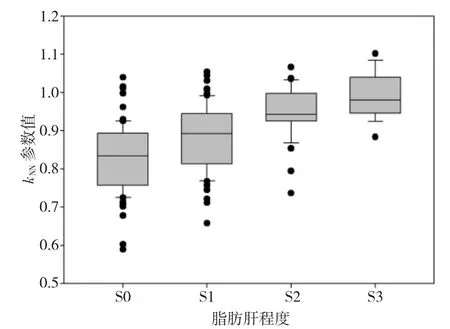
图9 基于神经网络估计的超声背散射零差K 模型kNN 参数值与脂肪肝程度的箱形图

利用神经网络估计的超声背散射零差K 模型αNN和kNN成像诊断不同程度脂肪肝的ROC 分别如图10、11 所示。αNN和kNN成像诊断脂肪肝程度≥S1、≥S2、≥S3 的AUC 值分别为0.77（95%CI：0.70～0.84）、0.84（95%CI：0.78～0.89）、0.87（95%CI：0.80～0.93）和0.77（95%CI：0.70～0.84）、0.84（95%CI：0.79～0.90）、0.84（95%CI：0.77～0.91）。上述结果表明，αNN和kNN成像诊断脂肪肝的性能良好。

图10 基于神经网络估计的超声背散射零差K 模型αNN 成像诊断不同程度脂肪肝的ROC

利用传统RSK 法和XU 法估计的超声背散射零差K 模型αRSK和αXU成像诊断脂肪肝程度≥S1、≥S2、≥S3 的AUC 值分别为0.561（95%CI：0.480～0.643）、0.573（95%CI：0.485～0.660）、0.526（95%CI：0.388～0.664）和0.753（95%CI：0.682～0.824）、0.829（95%CI：0.773～0.886）、0.809（95%CI：0.726～0.892）。相比传统RSK 法和XU 法，本研究提出的基于神经网络估计的超声背散射零差K 模型参数具有更好的脂肪肝程度评估性能。

图11 基于神经网络估计的超声背散射零差K 模型kNN 成像诊断不同程度脂肪肝的ROC

3 结语

近年来，超声组织定征技术在肝脏评价中受到广泛关注[18-19]。本研究提出了基于神经网络的超声背散射零差K 成像评价脂肪肝的新方法。

从理论上分析，肝脏发生脂肪变性后，多余的脂肪滴贡献了额外的散射子，导致脂肪肝的散射子个数多于正常肝脏，且脂肪肝程度越严重，散射子数量越大，这可能是超声背散射零差K 模型α 参数成像能够检测脂肪肝的理论基础。此外，当散射子数量越来越多，导致弥漫散射子的局部聚集[20]，也可能产生相干散射子，致使相干散射信号与弥漫散射信号的比值增大，这是超声背散射零差K 模型k 参数成像检测脂肪肝的理论推测。

计算机仿真实验结果和临床实验结果表明，相比传统RSK 法和XU 法，本文提出的基于神经网络的超声背散射零差K 成像方法整体上提高了估算精度，提高了脂肪肝评估性能，可为定量超声评价脂肪肝提供一种新手段。

本研究仍具有不足之处，虽然在整体估算精度上较优，但是在RB 指标方面所提出的神经网络法并不优于传统RSK 法和XU 法。由于神经网络法可以允许多个特征参数输入，因此具有较高的灵活性。在未来研究中，可设计新的特征参数，并相应改进神经网络结构和训练方式，以进一步提高神经网络方法的估算精度。