多角度探究2022新高考Ⅰ卷多选压轴题

莫 祺

广东省广州市真光中学 (510380)

2022年新高考Ⅰ卷多选的压轴题是一道函数性质与导数综合题，要求学生在抽象函数的背景下，理解函数的奇偶性、对称性、导数等概念以及它们之间的联系，对数学抽象、直观想象、逻辑推理等核心素养都有较高的要求.

一、考题呈现

C.f(-1)=f(4) D.g(-1)=g(2)

本题是2022年新高考1卷的第12题，是2021年新高考2卷单选压轴题的拓展延伸，综合性更强.除了考查抽象函数的性质之外，还考查了原函数与导函数对称性之间的关联，解题的关键是根据题干的条件得到原函数和导函数的对称性，再准确把握原函数与导函数图象间的关系.下面将从定义、图象、特殊函数等几方面解析这道题.

二、解法研究

1、从函数性质定义和复合函数求导的角度

2、从函数图象变换和导数几何意义的角度

3、从特殊函数验证的角度

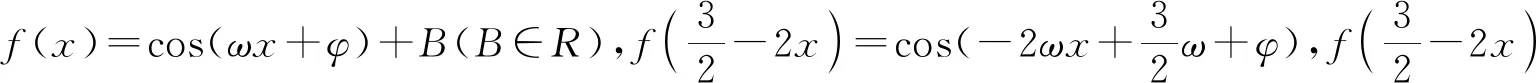
三、拓展延伸

解法1涉及了原函数与导函数在周期性上的联系，解法2涉及了原函数与导函数在对称性上的联系，但没有严格的证明.下面给出原函数与导函数在奇偶性、对称性、周期性上的命题，并给予证明.

命题1 若f(x)是偶(奇)函数且可导，f′(x)是奇(偶)函数.

证明：设f(x)为偶函数，则f(x)=f(-x)，由复合函数求导：f′(x)=-f′(-x)，f′(x)为奇函数，同理可证f(x)为奇的情况.

命题2f′(x)为偶(奇)函数且可积，f(x)可以表为一个奇(偶)函数与一常数之和.

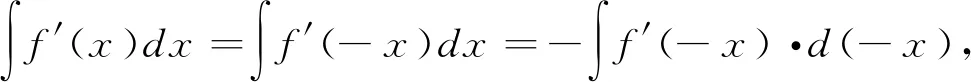
命题3 若f(x)关于x=a对称且可导，则f′(x)关于点(a,0)对称.若f(x)关于点(h,k)对称且可导，则f′(x)关于x=h对称.

证明：若f(x)关于x=a对称，则f(x)=f(2a-x)，两边求导得f′(x)=-f′(2a-x)，故f′(x)关于点(a,0)对称，同理可证f(x)关于点(h,k)对称的情况.

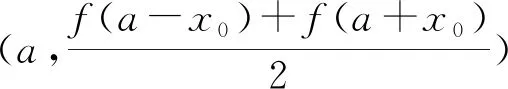
命题5 若定义在I上的函数f(x)的导函数f′(x)图象关于点(a,b)对称，则当b≠0时，函数f(x)不关于直线x=a对称；当b=0时，存在x0，若a-x0，a+x0∈I，使得f(a-x0)=f(a+x0)时，函数f(x)图象关于x=a对称.[1]

命题4、5的证明见参考文献[1].

命题6 若f(x)是周期为T的函数时，f′(x)也是周期为T的函数.

证明：已知f(x+T)=f(x)，则两边求导有f′(x+T)=f′(x)，即f′(x)是周期为T的函数.

命题7 若f′(x)为可积的周期为T的函数，且f(T)=f(0)，则f(x)也是周期为T的函数.

原函数与导函数的关系不仅体现在单调性与最值问题上，而且在对称性、周期性等性质上也有很大的关联性.虽然上述的一些证明使用积分，但是深入理解概念和熟悉图象变化特征也是能得到上述结论的.因此，在平时的教学中，一定要重视概念的讲解，加强数学思想方法的训练，避免机械式做题，注重一题多解、一题多变，强化新情境下数学本质的理解.