基于分布式电源出力独立随机性的配电网随机潮流算法
王玥娇,郭俊山,王 辉,田珊也,蒿天衢,张兴友
(1.国网山东省电力公司电力科学研究院,山东 济南 250003;2.山东大学,山东 济南 250016)
0 引言
“碳达峰、碳中和”是我国政府对世界的庄严承诺。预计到2050 年,我国70%的电量将来自风光发电。2020 年我国新能源新增装机1.2 亿kW,预计到“十四五”期间仍将以每年新增1.3 亿kW 的速度发展[1]。分布式发电(Distributed Generations,DGs)的容量一般在几十千瓦到数兆瓦之间,以接入35 kV及更低电压等级配电网为主[2-4]。“十四五”期间,山东规划了500 万kW 城镇光伏发电、1 000 万kW 乡村分布式光伏发电和50 万kW 分散式风力发电项目。分布式发电因其一次能源的不确定性具有显著的波动性和间歇性。多能互补的区域能源系统成为进一步扩大新能源发电规模同时稳定电网潮流的有效形式。在此背景下,不同形式的DGs 对配电网影响越来越显著,为了有效规划电源分布,研究和开发含不同类型DGs的新的配网潮流算法尤为重要[5]。
“随机潮流”的概念由BORKOWSKA 在1974 年提出[6],传统的确定性潮流算法中,输入变量和输出变量皆为确定值,而随机潮流(Probabilistic Load Flow,PLF)计算中,负荷、发电机的有功功率、无功功率等变量不再是确定值,而是服从一定概率分布的变化量,并由此计算出状态变量和支路潮流的概率分布及所需的概率统计指标。PLF 计算在实践中依据不同的建模、求解方法,演化出多种研究方法。目前,PLF 算法大体可归类为解析法和模拟法两大类,根据采用的计算方法又可分为卷积法、蒙特卡洛模拟法、点估计法和半不变量法等[7-17]。
文献[7]基于分布式发电的随机性特征,通过Gram-Charlier 级数展开,分析输出的随机变量的概率分布。文献[12]对微电网潮流进行了预测,考虑了光伏发电和风力发电的相关性,应用联合概率密度分布及马尔科夫链和拉丁超立方抽样方法进行PLF 预测研究。文献[13]和[14]将马尔科夫链、蒙特卡洛法同时结合应用,仅考虑到风力发电的随机性,对不同运行模式下微电网的潮流进行分析预测。目前,国内外学者对蒙特卡洛模拟法、点估计法[15-16]、一次二阶矩法[17]和半不变量法等PLF 算法进行了多方面的研究。
受地理微环境因素影响,同一配电网区域内不同光伏电站的光照强度、不同风场的风速总体趋势存在一致性,具体量测数值存在差异性,导致相关的光伏发电和风力发电等分布式发电出力也具有相似性。针对同一区域内分布式发电的相关性,提出一种基于三阶多项式正态变换的计及多种分布式电源相关性的PLF 算法,改变了传统PLF 只能利用独立的新能源发电系统有功出力概率空间的限制,本方法将相关随机性有功出力进行转换,使PLF方法应用范围得到推广。将研究中具有相关性的考虑多种影响因素的多种新能源发电出力转换为传统PLF 可以利用的独立非正态分布的有功出力概率,利用蒙特卡洛或三点估计等方法求出估计值,由确定性潮流进行计算,进一步通过Gram-Charlier 级数展开拟合出曲线。以高比例分布式发电配电网为例,仿真验证考虑风光发电相关性的潮流分布情况。
1 三阶多项式正态变换
多项式正态变换方法(Polynomial Normal Transformation,PNT)于1978 年 由FLEISHMAN 提出[17],可以用于求取非正态分布的新能源发电系统随机有功出力。三阶多项式正态变换(Thirdorder Polynomial Normal Transformation,TPNT)的原理及其在多维随机变量解析中的应用如下。
1.1 单个随机变量TPNT
设非正态分布变量P,TPNT 是利用服从正态分布的随机变量Q对P表示出来,表达式为
式中:P为随机变量;Q为服从正态分布的随机变量;a,b,c,d均为三阶多项式系数。
式(1)成立需要满足式(2)和式(3)的条件。
各系数a,b,c,d的值可由矩法(Product Moment,PM)、Fisher-Conish(FC)级数法或L-Moment Estimation(LM)法求得[18]。
1.2 多维随机变量三阶PNT
对于具有非正态分布形式的多维随机变量矩阵X,X的相关系数矩阵RX=[ρXij]m×m在被求得后,进一步处理得到符合正态分布的随机变量矩阵Z的相关系数矩阵RZ=[ρZij]m×m。其中,ρXij和ρZij为系数矩阵对应元素,存在函数关系,且满足条件为:
需要将满足正态分布的随机变量矩阵Z的相关系数矩阵RZ去相关性。设服从标准正态分布且独立的多维随机变量矩阵S,对矩阵RZ进行Cholesky分解,得出下三角矩阵L,其关系式满足:
由式(8)将多维相关性随机变量矩阵X进一步变换为服从正态分布随机变量矩阵S,其中A、B、C、D为对应系数矩阵。通过TPNT 去除了随机变量的相关性,使输入变量变为独立、服从标准正态分布的随机变量。再经过反变换,变换为去相关性的非正态分布随机变量,为PLF 计算提供符合条件的随机输入变量。
2 Gram-Charlier级数展开
在PLF 计算结果的处理中,通过Gram-Charlier级数展开分析支路输出功率、相应节点电压,描述其概率分布并绘制图形。Gram-Charlier 级数展开可在函数f(x)表达式未知时,利用特定的数学计算流程处理,相应可求出f(x)的前k阶矩阵Mk[7],即
式中:n(x)为连续正函数;Ck为第k项系数;m0(x),m1(x),···,mk(x)为n(x)的正交多项式,各多项式需要满足的正交条件如式(10)所示。
式中:a=0,1,2,…,k;b=0,1,2,…,k。
f(x)每一项的系数Ck为
综上,任一随机变量x的概率密度函数f(x)都可以通过对应随机变量前k阶矩阵的求解来获取。实际工程应用中,随机变量的概率密度函数和累积分布函数通常是通过符合标准正态分布的概率密度函数及累积分布函数求得。因此,推广至随机变量矩阵X,求得其前k阶矩阵,即可得到其概率密度的函数f(X)表达式。
设μX为随机变量矩阵X的均值,标准差为σX,标准化后X′=(X-μX)/σX,概率密度函数f(X)和概率分布函数F(X)的表达式为:
式中:Φ(X′)为标准正态分布函数;φ(X′)为标准正态分布概率密度函数。
在PLF 计算中,常用到前六项系数,如式(14)所示,σ为标准差、β为中心矩。
3 计及分布式发电相关性的配电网潮流计算
地理位置相近的分散式风力发电或分布式光伏发电,由于风速、光照强度之间存在一定的关联,因此其出力也存在相关性,其相关系数矩阵可通过历史数据进行拟合[19]。基于多项式正态变换处理含相关性非正态分布随机变量的概率问题可参考文献[20-21]。通过TPNT 变换,同一配电网区域内各风力发电、光伏发电之间的相关性可以去除。基本步骤为,将具有相关性的光伏发电和风力发电随机出力进行相关性处理,由PNT 变换到独立正态空间。然后对独立正态空间采样,依据相对应的系数矩阵映射关系进行逆变换,返回原变量空间,最终得到去相关性的考虑多种影响因素的非正态随机发电出力以应用于PLF计算中。
基于以上计算结果,可利用蒙特卡洛、三点估计等方法求取各新能源节点功率的估计值,然后应用确定性潮流算法,计算得到支路功率、节点电压的点估计值,并进一步计算其中心矩,利用Gram-Charlier级数展开绘制出分布曲线,从而实现计及具有随机性的分布式发电相关性的配电网潮流计算。具体步骤如图1所示。
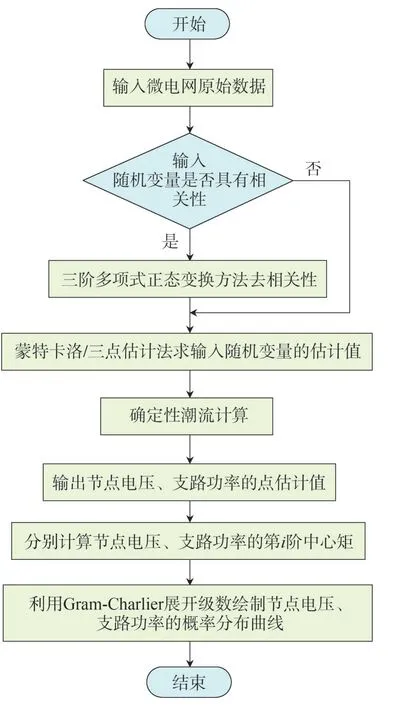
图1 考虑分布式发电随机相关性的配电网PLF计算方法
常见DGs 有风力发电、光伏发电、燃料电池和储能系统。在分析时,须注意其不同的出力概率特性及因其接入电网的方式不同表现出的节点特性。
光伏发电系统的有功出力,如果不考虑弃光,直接由光伏发电系统所在地区的光照强度决定,因此其概率密度为光照强度的概率密度乘以代表其光电转换效率的系数。分析数个地区历史光照的数据发现,光照强度的概率密度曲线大致呈现贝塔分布[20]。光伏发电系统所发电力需要经电压源型逆变器转化为交流电能,在进行电力系统分析时通常把其并网点作为PV节点考虑。
风力发电系统输出的有功出力与风速直接相关。但与光伏发电系统出力不同,光伏发电系统几乎可以利用所有光照强度下的一次能源产生电能,而风力发电机组无法利用所有风速下的风能,小于切入风速的风能因摩擦损耗、电机启动等原因无法被利用;大于切出风速的风能受风力发电机组机械应力与机组电气容量的限制,无法全部利用,当风速大于额定风速、小于切出风速时,风力发电机组出力不变。在以上因素的影响下,风力发电机组的出力概率曲线可由威布尔分布曲线进行描述[21]。在进行电力系统分析时,风力发电机组的并网点通常作为PQ节点考虑。
4 仿真测试与结果
研究采用MATLAB 进行编程并进行仿真测试。首先建立仿真模型,模型基于一个含有多种DGs 的配电网系统,各支路中分别包含多种DGs 和负载的组合形式,各DGs 所发电能经电力电子变换器以交流形式并网,电压等级为380 V,各线路长度以及线路连接示意如图2 所示。在提取到独立非正态分布新能源电源出力估计值后,确定性潮流算法应用牛顿-拉夫逊法。
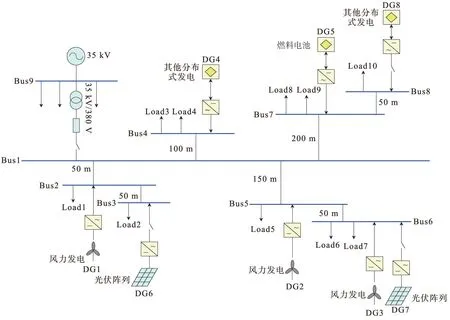
图2 含分布式发电的配电网
仿真中,由于3 个风力发电单元DG1、DG2 和DG3 的空间距离较近,可知其风速具有相关性,DG6、DG7 同为光伏电站,与风力发电单元出力之间的关系类似,同理可知其光照强度也具有相关性。相关性系数处理上均采用LM 法。根据相关研究结果,光强概率密度的曲线形状与贝塔分布曲线最为接近,光照强度概率分布曲线的形状与威布尔分布最为接近,通过调节贝塔分布和威布尔分布中决定其最终形状的参数,可建立随机的光照强度和风速模型[20-21]。基于以上研究结论,本研究开展的仿真验证中,光伏出力和风力发电机组出力分别服从贝塔分布和威布尔分布。
3 个风场风速相关系数以式(15)中矩阵R11表示,转换为服从正态分布空间的相关系数矩阵可得R21,如式(16)所示;同理,两个光伏电站的光照强度相关系数矩阵R12,如式(17)所示,可转换为正态分布空间的相关系数矩阵R22,如式(18)所示。
光照强度和风速的三阶多项式系数如表1所示。表2 给出了含相关性的风光发电出力处理后的数学期望。

表1 光照强度和风速三阶多项式系数
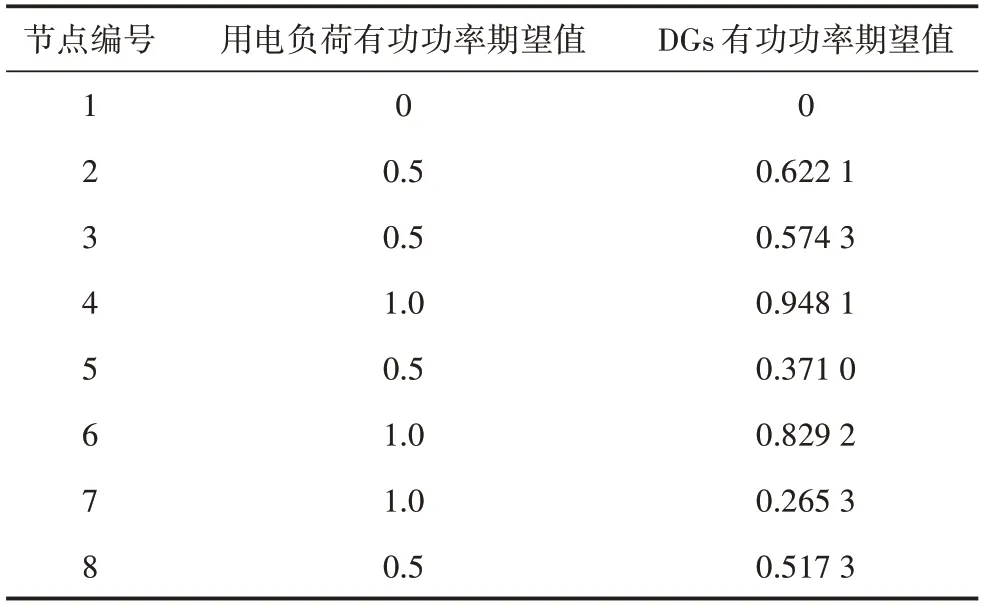
表2 含相关性输入变量的各节点有功功率期望值 单位:pu
以电网末端的节点6和节点7为例,分析配电网的电压质量。节点6 具有光伏发电和风力发电的相关性,图3 显示了其电压概率密度曲线,电压波动范围为0.93~1.02 pu,波动值为0.09 pu。节点7 的电压概率密度曲线如图4所示,电压范围为0.97~1.02 pu,波动值为0.05 pu。分析可知因节点7 中接入了燃料电池发电机组,其有功出力可控性高,对比节点6 的电压情况,其电压质量也较高。
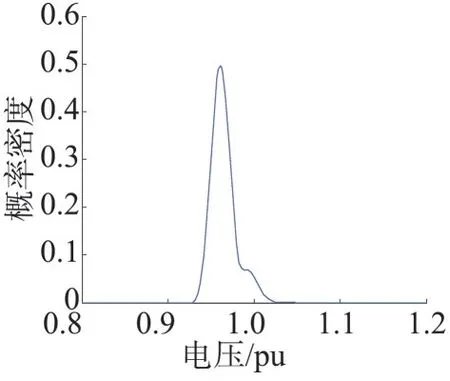
图3 节点6电压概率密度曲线
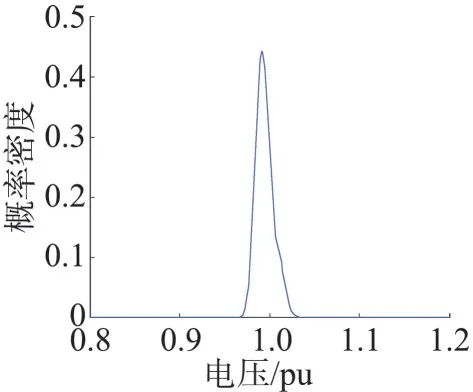
图4 节点7电压概率密度曲线
图5、图6 给出了经TPNT 变换后,利用三点估计法和蒙特卡洛模拟法得到的节点6、节点7 电压概率分布曲线对比图。由曲线可以看出,考虑输入随机变量的相关性后,TPNT 变换得到的独立非正态随机变量可以很好地应用到潮流算法中,在三点估计法和蒙特卡洛模拟法中都可有效应用,针对具备相关性输入随机变量的配电网PLF 是可行有效的,可以推测出考虑分布式发电区域相关性更贴近电网实际运行情况。
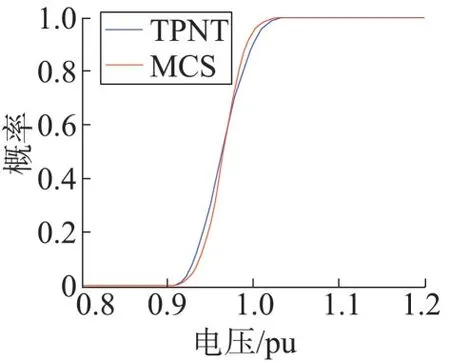
图5 节点6电压概率分布曲线
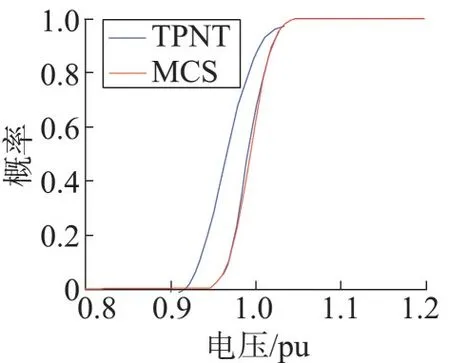
图6 节点7电压概率分布曲线
图7、图8给出了利用Gram-Charlier 级数展开后绘制的支路7—1、7—8 潮流概率密度曲线。从图7可以看出,由于DGs 出力随机性、波动性的影响,支路7—1的功率流向大多数情况下由节点7到节点1,但当DGs 出力不足时,有功潮流可能也会反向变为由节点1 到节点7。图8 说明支路7—8 有功功率主要在小于0.35 pu 的范围之内波动,功率流向为从节点7流向节点8。
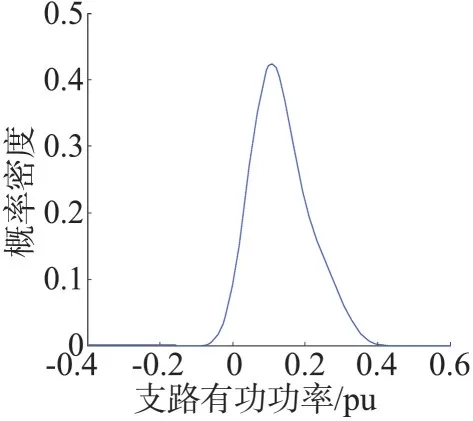
图7 支路7—1潮流概率密度曲线
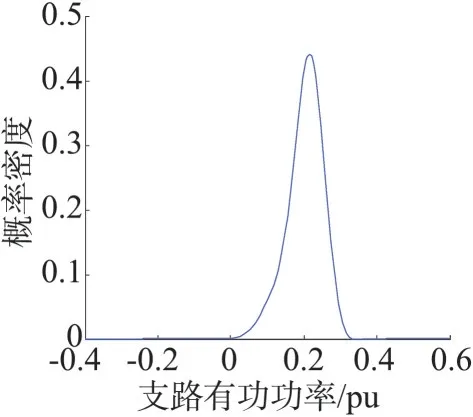
图8 支路7—8潮流概率密度曲线
5 结语
针对同一区域配电网中不同分布式发电单元具有的随机性、波动性以及相关性特点,提出一种考虑分布式发电单元出力相关性的变换算法,并将其应用到随机潮流计算。该算法将具有相关性的不同新能源出力利用TPNT 变换为考虑多因素影响的独立非正态随机出力,进一步通过随机潮流的计算,获得相应的概率统计特征。仿真结果表明,所提出的潮流算法灵活、简洁、应用范围广,且具有较好的准确度,可应用于随机潮流计算的数据处理中。经分析验证,所提方法能够合理反映高比例分布式发电配电网的稳态运行特性,对高比例分布式发电配电网运行和规划有一定的指导意义。

