计及电压不可行分区的配电网无功规划方法

郭 杉，杜 波，安 东

（1.内蒙古电力科学研究院，内蒙古 呼和浩特 010020；2.巴彦淖尔电业局，内蒙古 巴彦淖尔 015000）

0 引言

中压配电网电压质量不仅直接影响用户用电体验，亦对低压配电网有较大间接影响。因此，如何改善电压质量始终是配电网运行需要解决的现实问题。中压配电网（10 kV）电压质量问题主要出现在农村及具有农村配电特性的城乡结合区域，以低电压问题为主［1］。主要技术因素包括供电半径过长、线路线径过细、负荷过大、无功容量不足等。由于电压严重跌落，线路有功损耗也将大幅提高［1］。

一般通过技术改造解决低电压问题［1］，改造方法主要包括线路改造、负荷拆分及无功调整等。改造方法主要包括线路改造、负荷拆分及无功调整等。通过线路改造更换导线，选取线径更大的导线，并缩短供电半径［2-3］。通过负荷切改，将线路原负荷分配至其他线路，降低线路负荷。无功调整方式则是通过调整线路无功容量及分布，实现“升压降损”。无功调整设备主要包括线路调压器、并联电容器、静止无功发生器（Static Var Generator，SVG）等。与线路改造及负荷切改相比，无功调整的成本低、周期短，是常用的方法。但在配电网工程实践中，经常发现无功设备容量及位置选取不当，导致无法达到预期效果。通过无功规划，使无功设备的选址定容兼具科学性与经济性，是无功调整的关键所在。当配电系统规模较大时，可采用“分而治之”的思想，对原网络进行分层、分区或二者结合。文献［4］对10 kV配电网络进行分层分区。区域内充分利用分布式电源和无功调节设备，区域间则采取区域协调控制器进行协调控制。尽快能够实现电压无功分层分区精确控制，但区域间需部署多台区域协调控制器，区域内全部可控设备均需接入区域控制器，成本较高，不适合大范围推广。文献［5-10］则只对配电系统分区而不分层，主要研究分区的识别方法，针对分区建立无功优化模型。需要注意，无功规划结果与负荷分布特性有较高的关联度，如何建立负荷模型也是无功规划问题的关键点之一。文献［11］提出一种基于极限场景的两阶段配电网无功优化方法，首先将电源有功、无功功率、无功设备可用容量等连续变量及变压器抽头、电容器组数等离散随机变量均取极限值从而构成极限场景，并针对极限场景建立等式及不等式约束，求解无功优化问题。文献［12］则采用概率建模技术生成大量负荷场景，并采用Wasserstein 距离指标和K-means 聚类缩减场景数量，进而找出无功最优场景。在建立无功优化模型后，通常有两种求解方法，分别是数学规划法和基于种群进化的优化算法。数学规划方法［13-17］虽可能找出最优解，但对问题的边界条件要求严格；进化优化算法包括遗传算法、和声搜索算法［18］等。该类方法虽不能找出最优解，但对问题的性质和规模没有严格限制和要求，因此具有更广泛的适用性。

首先定义电压不可行分区的基本概念，提出两种典型的负荷分配场景。然后建立无功优化模型，并对传统引力搜索算法进行改进，避免陷入局部最优，另外在个体速度计算时，采用粒子群优化算法的速度更新方式，解决随个体质量变大导致的收敛速度变慢的问题。再选取某34 节点真实的10 kV 配电系统对算法加以测试，验证算法的可行性，并对结果进行分析。

1 计及不可行分区的无功规划算法

1.1 基本概念

给出配电系统不可行节点及分区的概念。已知某配电系统节点集合为N，对任意节点ni∈N，若其电压幅值u（ni）∈（Umin，Umax），其中Umin、Umax分别为节点电压允许的上下限幅值，则ni为电压不可行节点。可见，所谓电压不可行节点即电压幅值不在允许范围内的节点。观察电压不可行节点的分布，通常位于主干及分支的末端，且潮流方向上的后续节点大概率亦为不可行节点。即电压不可行节点往往以分区的形式出现，由此引出电压不可行分区的概念。已知N′为该配电系统的电压不可行节点集合。有节点集合ζ 且ζ⊂N′，若ζ中任意节点，在ζ中均能找到至少一个节点与之存在连接关系，而对N′-ζ中任何节点，与ζ中任意节点均不存在连接关系，则ζ中节点构成一个电压不可行分区。

对于结构简单、分支较少的小规模配电系统（节点数低于30），通过潮流仿真，在潮流方向上首个不可行节点进行补偿，通过几次迭代即可消除不可行节点，实现无功平衡及电压调整。但对于中大型配电系统，往往含有多个分支、拓扑复杂，如果采用上述方法，则需要多次迭代。另外，实践中配电系统对无功调整位置数量有明确限制，如果针对单点进行补偿，很可能超过上述限制。因而考虑将复杂的配电系统分成多个小规模的电压不可行分区（即分区），每个分区最多选取一处进行补偿。一旦各分区满足电压无功约束，则全系统必满足电压无功约束。另外，针对补偿点过多的问题，可在多个分区首节点的公共前驱节点进行补偿，避免补偿位置过多的问题。使所提算法更好地适用于中大型配电系统。

1.2 负荷分配两种模型

无功规划的结果与负荷分布密切相关。目前最常用的做法是使用实际负荷数据。但随着系统规模增大，获取实际负荷数据的难度亦有所增大。而另一方面，系统总负荷及功率因数是易于获取的，因而提出两种基于系统总负荷的负荷分配模型。

首先给出节点负荷因子概念。节点i的负荷因子li等于节点的获得功率Si与额定功率SEi之比，即

配电系统的负荷因子也通过式（1）计算。分子为系统端口功率，分母为线路各节点额定功率代数和。

等负荷因子模型认为各节点负荷因子与配电系统负荷因子相等。各节点获得功率等于节点额定功率乘以配电系统的负荷因子。

末端集中模型认为负荷主要集中于末端。首先需要设定末端分区的负荷因子ltail，即末端负荷与系统负荷之比。利用式（2）获得末端分区的获得负荷，再利用式（3）计算各末端节点的符合因子。然后根据式（1）确定各末端节点的获得功率。采用同样的方法可得到非末端节点的获得功率。

式中：Stail为末端分区的获得功率；S为配电系统总功率；STi为末端节点i的额定功率；lti为末端节点i的负荷因子。

采用上述两种模型的原因为：等负荷因子模型认为各节点（配电台区）获得功率与其额定功率比值相同，即额定容量较大的节点，其获得功率也较大，此种假设与人们主观认知一致。而末端集中模型认为负荷集中于系统末端，与其他负荷分配方式相比，此种模型末端节点的电压波动幅度更大，满足该方式的无功规划方案亦能大概率胜任其他场景。

1.3 计及电压不可行分区的无功规划算法

计及电压不可行分区的无功规划算法主要流程如图1 所示。首先输入各参数，主要包括各段线路型号、系统总负荷、功率因数及所允许的补偿位置数Cmax。然后根据潮流计算结果，确定电压不可行节点，自动识别电压不可行分区。计算无功缺额，在不可行分区首端进行补偿。返回潮流计算，重复上述过程，直至补偿位置超过约束条件或无不可行分区。如果在给定约束条件下，找到补偿方案，则进行无功容量优化，返回优化结果，算法结束。

图1 基于电压不可行分区的无功规划算法

对上述算法说明如下：

1）配电系统基础参数主要包括节点间各段线路的长度、阻抗及导纳。运行参数主要为各节点的负荷，包括有功功率及无功功率。考虑到实践中无法获取各节点负荷，通常只能获取线路首端的功率，故定义典型场景将首端负荷合理分配至各节点。根据农村电网无功补偿要求，一条中压线路补偿位置通常不超过2处，Cmax通常取2。

2）配电网常用潮流算法包括牛顿-拉夫逊及快速解耦法。当配电系统规模较大时（100节点以上），宜采用快速解耦法，在保证计算精度的前提下，运算时间低于牛顿-拉夫逊法。通过潮流计算，获取全部电压不可行节点后，根据配电系统拓扑结构，利用节点间连接矩阵确定各不可行分区。

3）对电压不可行分区，按照单位功率因数确定分区内各节点的无功缺额，并在分区潮流方向首节点集中补偿。如果当前电压不可行分区不止一个，考虑到补偿点数量的限制，应在多个分区的共同前趋节点进行集中补偿。

4）通过将中大型配电系统依据电压可行性进行分区，在无功优化过程中，只需要专注处理电压不可行分区即可，实现了配电系统的化简，相比传统无功优化算法，本节算法在处理中大型配电系统时更具效率优势。

2 无功容量优化

2.1 优化模型

通过不可行分区集中补偿的迭代计算，消除电压不可行区域后，所得无功规划容量并非最优容量，可将其视为无功容量上限。进行无功容量优化计算。

无功容量优化计算以配电系统无功容量及有功网损最小为目标，目标函数为

式中：ω1、ω2为权重因子；假设i为被选中参与无功补偿的节点，Qi为节点i的补偿容量；Pl为网损；k为全部参与无功补偿节点数；fobj为无功容量优化目标函数值约束条件包括各支路潮流平衡约束及节点电压幅值。由于已掌握无功容量上限，因而将节点电压及无功容量写成罚函数形式得到增广目标函数，即

式中：λ1为电压越限的惩罚系数；λ2为有功网损的惩罚系数；λ3为无功补偿容量越限的惩罚系数；Vilim、Qilim分别为节点i电压及无功限值，定义如下：

式中：Qimax为节点i的最大补偿容量，由1.3 节中方法确定；Qi为节点i的补偿容量；Vi为节点i电压幅值；Vimax、Vimin分别为节点i的上下限幅值；Plmax、Pl分别为补偿前后的有功损耗。

2.2 基于改进GSA算法的无功容量优化

引力搜索算法（Gravity Search Algorithm，GSA）最早由文献［19］提出。GSA 算法借鉴物理学万有引力概念，在搜索空间中创建一系列个体，每个个体对应优化问题的某个候选解。个体的质量越大，说明该个体越接近最优解。同时对其他个体的引力越大，吸引其他个体向该个体靠拢。同时GSA 引入随机扰动因素，避免算法过早收敛。下面给出GSA 算法的基本概念。

搜索空间：给定某优化问题，假设目标函数为fobj，变量有m个。每个自变量有上、下限值，则由上下限值构成m维区域即为搜索空间。搜索空间中包含H个个体x1，x2，…，xH，每个个体包含位置、质量、距离、速度、加速度、引力等主要属性。

1）位置：即个体在m维搜索空间中的坐标，对应于目标函数的一个备选解。

2）个体质量：个体的质量与其适应度成正比，由式（8）计算。

3）距离：即搜索空间中不同个体间的欧氏距离。

式中：xi、xj分别为个体i、j的位置坐标；Rij为个体i、j的欧式距离。

4）个体引力：个体i在d维的引力是搜索空间中其余个体对其引力之和，即

式中：rj为［0，1］间服从均匀分布的随机数；Fij（t）为个体j对个体i在t时刻吸引力。ε为接近零的极小正数，以避免出现分母为0的情况；G（t）为引力系数，由式（11）计算。

式中：G0为引力系数初始值；α为衰减率，是预设常数。

5）获得引力后，利用式（12）—式（14）依次更新个体的加速度、速度及位置，即为

式中：ai（t）、Fi（t）、Mi（t）为个体i在t时刻的加速度、引力及质量；ri为服从［0，1］均匀分布的随机数；xi（t）、vi（t）为个体i在t时刻的速度及位置。传统引力搜索算法主要流程如图2所示。

图2 传统GSA算法流程

传统的GSA 算法存在容易陷入局部最优，且随个体质量逐渐增大，后期收敛速度衰减等问题［20］。因而需对传统GSA算法加以改进。首先为了尽可能避免陷入局部最优，计算个体引力时，只计算前k个质量最大的个体对其引力。

根据文献［21］借鉴粒子群优化速度更新方式，综合粒子群优化（Particle Swarm Optimization，PSO）算法粒子群的群体社会行为能力及GSA算法的本地搜索能力，将速度公式改进为

式中：w、c1、c2为权重因子；r1、r2为服从［0，1］均匀分布的随机数；xbest（t）为t代质量最大的个体。

分析GSA 算法位置更新公式，可知粒子位置变化主要取决于速度，而速度变化由加速度决定，加速度与适应度（即个体质量）成反比、与引力成正比，即粒子逐渐向适应度高的方向移动，从而实现目标优化。在进行无功容量优化应用时，设置个体的坐标维度与补偿点数一致，每个个体位置坐标代表了配电系统中各个电压不可行分区的无功补偿容量。GSA 算法运行终止后，适应度最高的个体坐标即为优化后的补偿容量。

3 算法测试

3.1 测试说明

以一条真实10 kV线路验证所提无功规划方法。算法通过Python 程序语言实现，潮流计算模块采用开源PyPower工具包。线路基本参数见表1。

表1 线路基本信息

该线路具备农村线路特征，供电半径长。干线线径150 mm2，支线为120 mm2及70 mm2混合。该线路负荷季节特性明显，6—9月为负荷高峰期，负荷主要集中于线路中后段。首端功率因数为0.89，低于0.9的标准值。线路简化拓扑如图3所示。

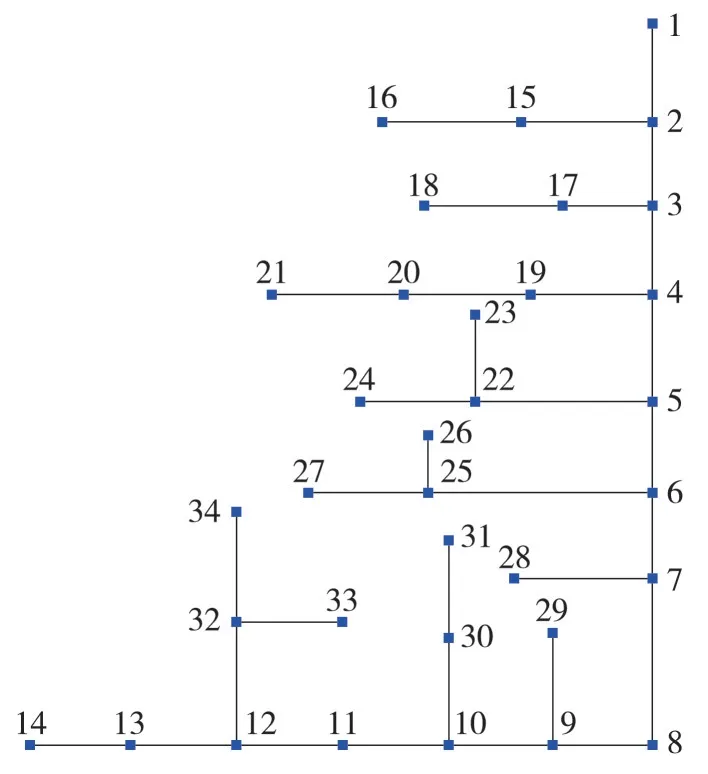
图3 10 kV配电线路的简化拓扑结构

3.2 仿真计算及结果分析

采用1.2 介绍的两种负荷分配方法，分配节点负荷。对于末端集中场景，设置末端负荷因子为0.5，即系统50%的负荷部署于末端，各节点功率因数与系统功率因数相等，均取0.9。末端节点包括｛10-14，30-34｝。另外，还应考虑未来负荷增长情况，故系统负荷分别取最大年负荷及120%最大年负荷加以分析。

10 kV节点供电电压合格区间为0.93～1.07 pu，考虑到线路为农网线路，将合格区间扩大至0.9～1.07 pu。四种场景的仿真结果见表2，各场景节点电压分布如图4 所示。根据表2 可知，除场景1（最大负荷-等负荷因子）外，其余3 种场景均存在电压不可行节点，且最低电压节点位置相同，均为节点14。分别对比场景1、2及场景3、4可以发现，采用集中于末端的分配方式，虽然系统总体负荷相同，但末端节点如节点13 和31 的电压明显低于等负荷因子场景，说明负荷的分布对节点电压有较大影响。

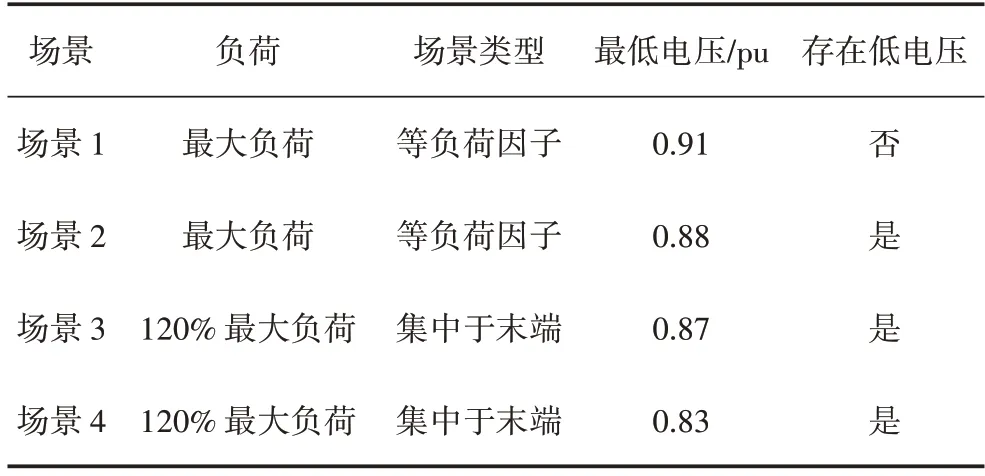
表2 四种场景仿真结果

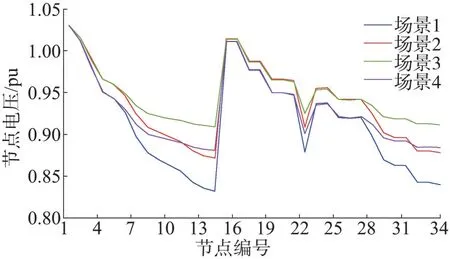
图4 四种典型场景下节点电压值

4 种负荷场景中，场景4（120%最大负荷-末端集中）的电压异常情况最严重。故针对场景4 进行无功规划。算法分为两个阶段。第1 阶段主要完成补偿容量计算。经过潮流分析，确定系统中存在一个电压不可行分区，由节点7 至系统末端，具体节点包括｛7—14，28—34｝。以单位功率因数，确定该分区所需无功补偿容量为877 kvar，在节点7 进行补偿。重复上述过程，得出节点11 需要补偿容量721 kvar，此时已无电压不可行分区，第1 阶段结束。第2 阶段利用2.2 节改进GSA 算法对进行优化计算，取G0=100，α=20，迭代次数t=50，得到结果见表3，在节点7 及11 补偿容量分别减小为659.2 kvar 及709.7 kvar。

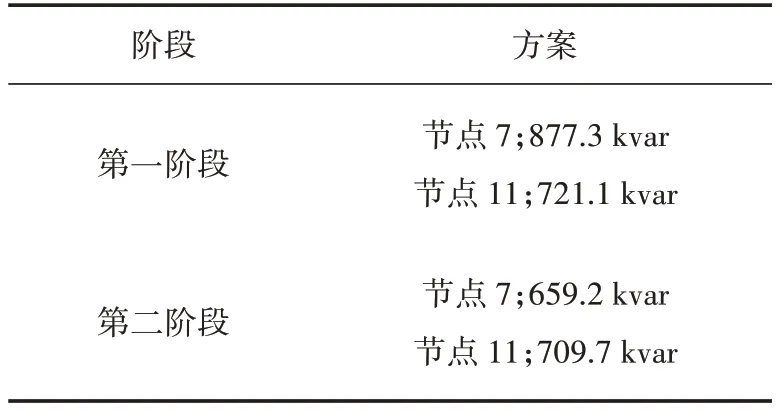
表3 无功优化结果

采用上述优化方案后，节点电压如图5 所示，各节点电压幅值如表4 所示。最低节点（节点14）电压由补偿前的0.83 pu 提升至0.90 pu，无功容量较优化前降低229.5 kvar，不仅能够满足节点电压约束，也体现了无功容量优化计算的必要性。

图5 最终优化方案对应电压值

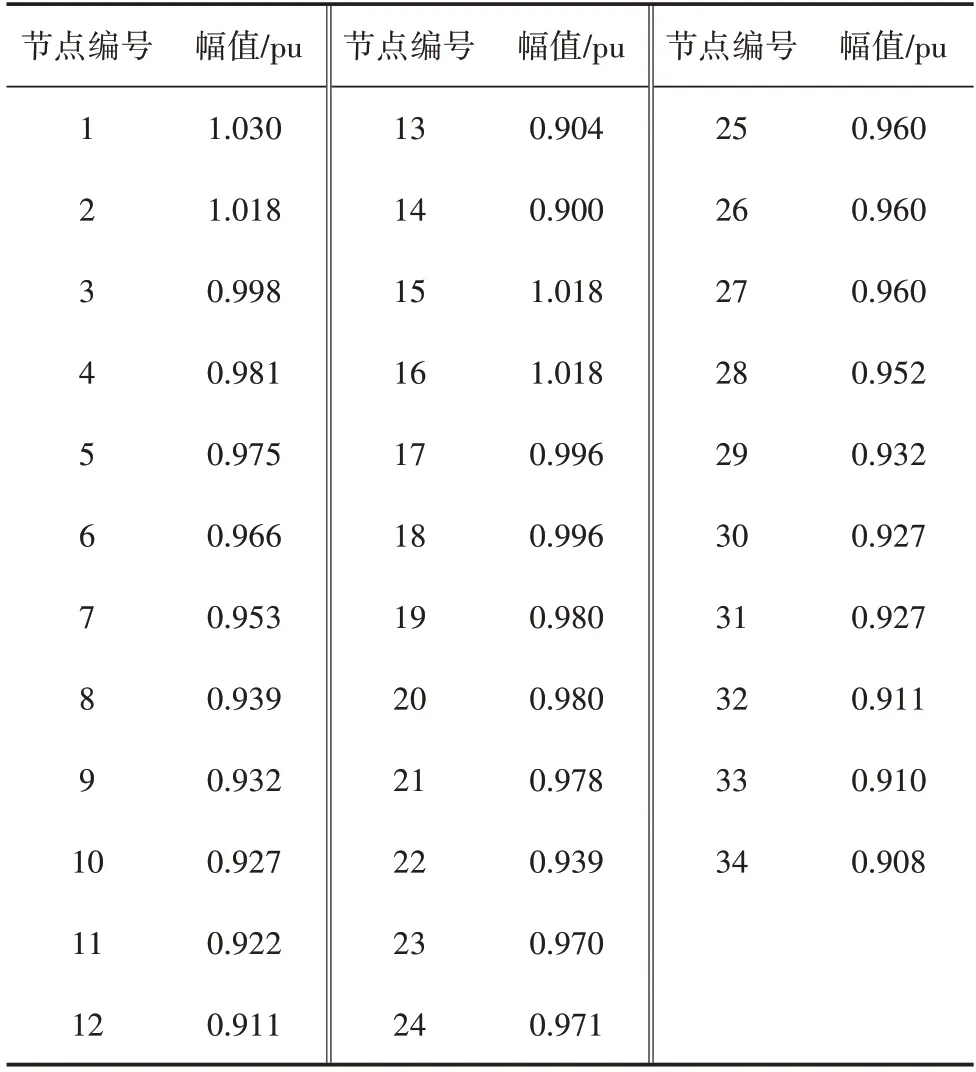
表4 经无功优化后场景4节点电压

4 结语

为高效解决配电系统的无功规划问题，定义电压不可行分区并给出两种负荷分配模型。以减小补偿无功容量、降低线损、提升电压质量建立目标函数，并分两阶段完成目标优化。第一阶段，识别电压不可行分区，进行分区集中补偿，以确定无功规划容量上限；第二阶段，采用改进的引力搜索算法，对无功容量进行优化计算，有效避免陷入局部最优及收敛速度衰减的问题。通过将无功规划的选址定容和容量优化解耦，旨在减小算法的搜索空间并降低计算开销，提升运算效率。利用10 kV真实线路对算法进行测试，验证所述算法的有效性。同时算法对不同网络拓扑的规模有较好的适应性，对于大型配电网络同样适用。后续将对算法进行扩展，使其能够应用于分布式光伏多点接入的配电场景。