点云模型的匹配点对优化配准

余永维， 王 康， 杜柳青， 瞿 兵

（重庆理工大学 机械工程学院，重庆 400054）

1 引言

三维激光扫描技术以其适应性强、自动化程度高和实时性等特点，很好地满足了先进制造技术发展的需求，成为工业上获取实体三维空间信息的重要方法之一。受到传感器行程、扫描位姿等因素的影响，不同视角获取的坐标点云通常具有一定重叠。通过点云配准获取相邻视角点云的匹配点对，解算其变换矩阵，将源点云和目标点云配准到同一坐标系，是重建出完整实体三维点云模型的重要方法。

Besl［1］提 出 的 迭 代 最 近 点（Iterative Closest Point， ICP）算法被认为是目前最经典的配准算法。该算法对完全重叠的点云具有优越的配准效果，但对点云部分重叠的情况适用性较差，同时算法依赖于较好的初始配准位姿。因此点云配准技术常常采用由粗到精的模式。

为解决点云的粗配准问题，业内学者已做了许多相关研究。主成分分析（Principal Component Analysis， PCA）是常用的数据分析方法，用于n维数据的降维处理，并基于原始数据构造全新的k维特征(k＜n)作为主成分。Li［2］提出了基于PCA的点云配准方法，分别获取待配准点云的主成分，将主成分间的变换关系近似为点云间的初步配准参数，并结合ICP完成点云的粗配准。除此之外，业内学者还提出了多种用于粗配准 的 算 法，例 如4PCS［3］，Super Generalized 4PCS［4］，NDM-KICP［5］，C-EGI［6］等。上述方法常用于为精配准提供较好的初值，由于需要计算点云特征，故一般耗时较长。精配准的目的是对粗配准结果进一步修正，从而得到更优质的配准结果。在ICP的基础上，许多学者就匹配的精度、效率等问题，对算法进行了改进。Ren［7］等提出了匹配点对选取的新策略，改进的算法通过引入特征点法线信息，减少了点对匹配的错误率，降低了完成配准所需的迭代次数。Yu［8］等提出了一种基于匹配点对二次滤波的改进ICP点云配准算法，首先对点云进行分割，提取实际参与配准的部分点云，使用二次滤波算法提高匹配准确度，最后对配准参数进行了求解。Pavlov［9］等对配准迭代过程进行了优化，提出了基于Anderson加速原理的AA-ICP算法，较大地提升了配准效率。上述算法都在一定程度上提高了配准的效率及准确性，但在处理具有点云部分重叠的配准工作中表现较差。为解决这一问题，Chetverikov［10］等提出了裁剪ICP算法（Trimmed Iterative Closest Point Algorithm，Tr-ICP），通过引入重叠率系数去除离群点，每次迭代保留固定比例的点，实现了低重叠率点云的有效配准，但算法计算速度较慢且对重叠率数值较为敏感［11］。在上述算法基础上，Dong［12］等提出了一种基于李群参数的LieTrICP算法，该算法结合了Tr-ICP和李群表示的优点，能够较好地应对具有缺失点、扰动和离群点的情况。此外，刘跃生［13］等提出了混合稀疏迭代最近点配准算法，抑制了离群值对配准的影响，在特征不明显且点云部分缺失的配准工作中也有较好的表现。

区别于迭代最近点及其改良算法，基于深度神经网络的点云配准方法［14-16］也得到了广泛研究。该类算法得益于深度神经网络对数据优秀的处理能力，能提取丰富的点云特征［17］，从而完成点云的匹配和刚性变换任务。但该类算法多数依赖于复杂的数据集以及特征提取方法，网络计算量较大，对配准的鲁棒性较差［18］，因此在实际应用中并不成熟。

针对传统迭代最近点（ICP）算法在处理点云部分重叠的配准工作时，配准误差大且适应性差的问题，本文优化了点云降采样策略，并结合Tr-ICP，提出了一种基于匹配点对加权优化的改进配准算法。使用改进的降采样算法获取参与配准的降采样点云，解决传统降采样算法与配准算法不契合问题的同时提高算法对噪声的鲁棒性。提出引入改进Sigmoid函数对具有小距离的匹配点对进行优化，克服Tr-ICP忽视小距离点对仍然可能是错误点对的缺点，实现点云的精确配准。

2 Tr-ICP算法原理

在实际应用中，噪声及非重叠区域引入的离群值，只会在目标点云中找到错误的匹配点对［19］，使得传统ICP算法在应对部分重叠的点云配准工作时可能失效。针对上述问题，Chetverikov［10］等提出了Tr-ICP算法。

给定源点云和目标点云构成的点集，分别记为X={xi，i=1，2，…，Nx}，Y={yi，i=1， 2， …，Ny}。点云重叠部分为X点集内满足与Y中对应点距离误差小于一定阈值的点所构成的最大子集P={pi，i=1，2，…，Np}，理论上这些点对都是应该是正确点对。定义重叠率ξ：

重叠率通常无法以视觉估计来获取，故算法给出最小化目标函数来求取：

式中：e为配准的裁剪均方误差（Trimmed Mean Squared Error，Tr-MSE）；λ为 预 设 参 数，取λ=2。算法主要执行如下步骤：

（1）对源点云中的每个点，搜索目标点云中的最近点，构建点对关系并计算距离平方；

（2）根据重叠度提取距离较小的前Npo个点对，作为参与配准的候选点对，并计算其和STS；

（3）根据候选点对，使用奇异值分解（Singular Value Decomposition，SVD）求解最小化目标函数，利用求得的刚性变换关系M(R，t)更新点集X。

重复上述步骤，直至满足迭代停止条件：

（1）迭代次数大于设定阈值Niter；

（2）Tr-MSE小于设定阈值；

（3）相邻迭代计算的Tr-MSE差值|e′-e|足够小。

Tr-ICP算法将距离较大的点对视为离群值剔除，但并未对距离较小的点对中可能存在的错误点对进行处理。同时算法易受到降采样方式的影响，当使用非均匀降采样时，若更多的采样到非重叠区域的点，会导致算法筛选出待配准点对中的正确点对更少，影响配准精度。

3 改进配准算法

3.1 改进均匀降采样算法

为降低原点云中离群值的影响，同时缩减数据量以提高配准的精度和效率，在配准点云前需要进行降采样处理。随机采样和基于密度函数的非均匀采样是ICP算法常用的采样方式。但非均匀的采样会影响Tr-ICP算法对参与配准点对的选取。过多的采样到非重叠区域的点，会使算法在计算点对距离并排序时，更多来自非重叠部分的点对被视为正确点对参与配准，抑制了算法对离群值的处理能力。因此，需要采用均匀的采样方法。

体素降采样是常用的均匀采样方法，将点云划分为n个均匀的三维体素单元，每个体素单元的 重 心pv(xv，yv，zv)，v=1，2，…，n，由 式（6）计算，通过重心pv代替体素单元内所有点pt(t=1，2，…，m)，以此实现均匀降采样。

但重心pv在原点云中并非真实存在，径直用于配准会增大配准误差甚至导致算法陷入局部最优。基于点云有效信息分布集中，而噪声等无效信息点离散性分布的特点，本文对体素降采样算法提出改进。对重心pv与其体素单元内所有点的欧氏距离dt(t=1，2，…，m)进行估计分析，dt近似服从高斯分布，计算其均值μ和标准差σ：

无效的噪声点通常分布在有效信息点云表面或远离有效点云，因此dt与均值μ差异愈小或愈大的极端点归类为离群值的概率更大。采用式（9）筛选出满足期望的有效点，区间外的点将被视作离群值剔除。通过标准差增益系数ω控制有效点筛选范围，ω越小筛选越严苛。满足条件的点构成集合Pi，对集合中的点按dt的大小有序排列，使用式（10）提取满足中值条件的点替换体素降采样算法计算的重心，使每个体素单元采样到原点云中真实存在的点。

n个三维体素单元采样点构成的点集作为参与配准的初始点集。提出的改进降采样算法能够均匀地提取到原点云上的点，避免了非均匀采样带来弊端的同时，提高了算法对离群值的鲁棒性。

3.2 基于匹配点对优化的点云配准方法

Tr-ICP算法对搜索到的匹配点对进行距离平方计算并排序，引入重叠率的概念提取前Npo个点对进行配准，将除此外距离较大的点对视为离群值剔除。该方法避免了非重叠区域点对参与配准，减少了参与配准的点对数量，提高了配准效率。而实际上，当点云配准处于初期阶段时，筛选出参与配准的点对，并非全为有效点对。

以重叠度为50%的标准及带均布噪声的样条曲线点云配准为例，如图1所示。点云重叠部分的理想匹配点对关系已知，使用k-dtree最近邻搜索构建匹配点对关系，并视对应点与理想对应点距离小于一定阈值的点对为有效点对，阈值由点云密度确定。绘制其参与配准的匹配点对以及有效点对分布直方图，如图2所示，并将基本信息记录于表1，对点对分布规律进行分析。

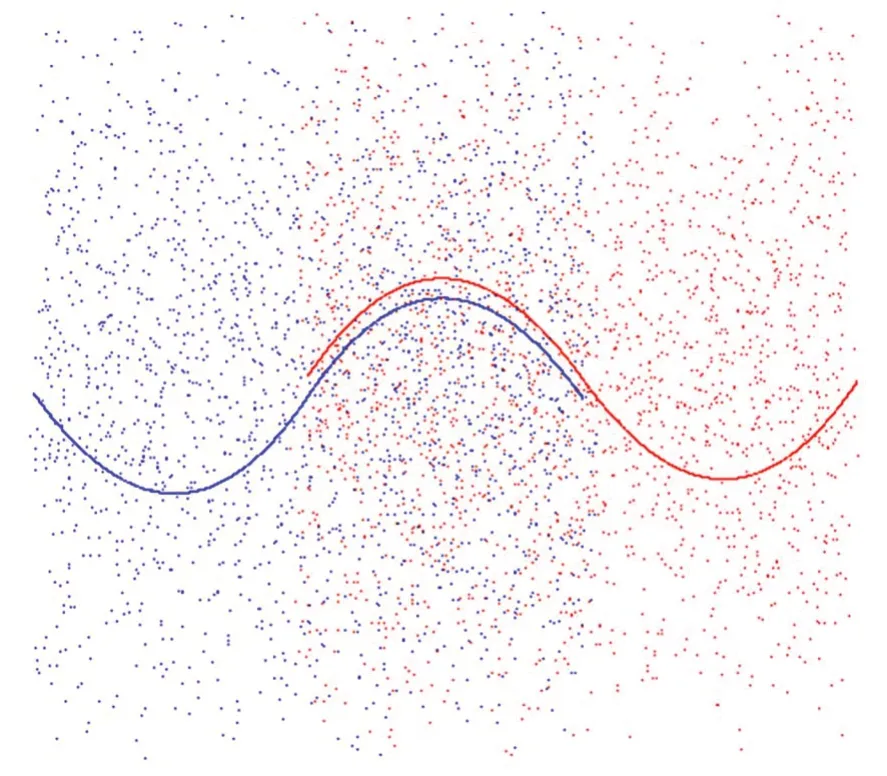
图1 带均布噪声的样条曲线Fig.1 Spline with uniform noise

结合表1可知，无论是理想还是带噪声条件下，传统Tr-ICP算法在迭代初期，其筛选的参与配准的点对有效率都较低。同时对比图2（a）、图2（d）及图2（b）、图2（e）可知，对于带噪声和不带噪声两种情况，有效点对均更多分布在距离相对较大的点对中，即距离较小的点对更有可能是错误点对。点云配准应更多的利用有效点对，降低错误点对的影响。

表1 样条曲线匹配点对基本信息Tab.1 Basic Information of spline matching point pairs

基于上述分析，本文针对Tr-ICP并未对存在距离较小的错误点对进行处理的问题，在算法原有基础上，引入平衡权重θ(i)，对距离相对较小的匹配点对分配较小的权重，以降低存在的错误点对对配准精度的影响。同时，结合图2（c）和图2（f）可知，随着迭代趋于后期，有效点对在距离相对较大的点对中分布比例变得更大，且更广泛，而距离相对较小的点对中，有效点对依然分布较少。因此，采用抑制距离相对较小的点对来提升配准效果的方法，对带噪声的情况依然适用。进而，可将原配准问题转化成如下目标函数的最小化问题：

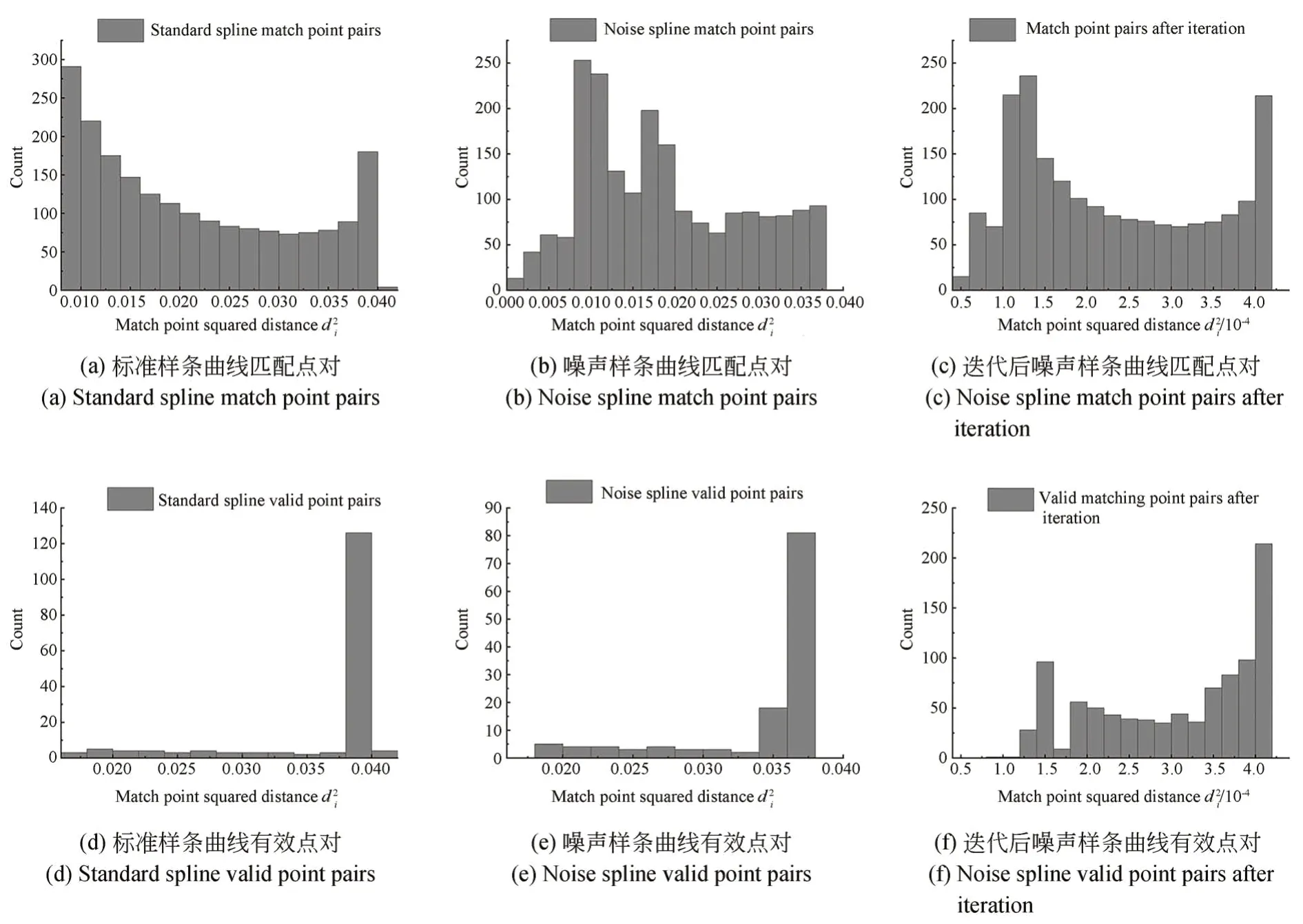
图2 样条曲线匹配点对分布图Fig.2 Spline matching point pair distribution plot

3.2.1 平衡权重确定

计算配准工作中所有匹配点对的距离并绘制曲线如图3，数据来自于重叠度约60%的Bun270和Bun315数据集配准工作，固定采样点数为10 000。Tr-ICP算法视其前60%的点对为参与配准的候选点对。

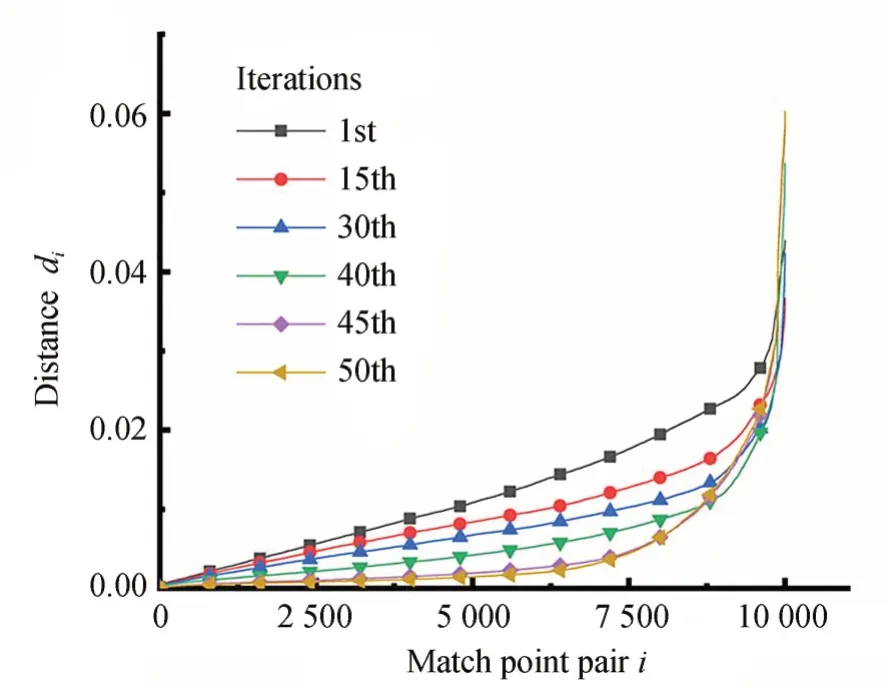
图3 匹配点对距离曲线Fig.3 Curves of match point pair distance

据上述数据所示，在配准迭代初期，参与配准的点对距离差异较大。距离相对较小的点对应该被分配较小的权重，以减小可能引入误匹配点对的影响。随着迭代次数增加，参与配准的点对距离变化愈发平缓，更多距离相对较大的点对应被分配较大的权重，以提高配准的精度。在此基础上本文引入改进Sigmoid函数如图4所示，构建了平衡权重和误差的自适应关联函数：

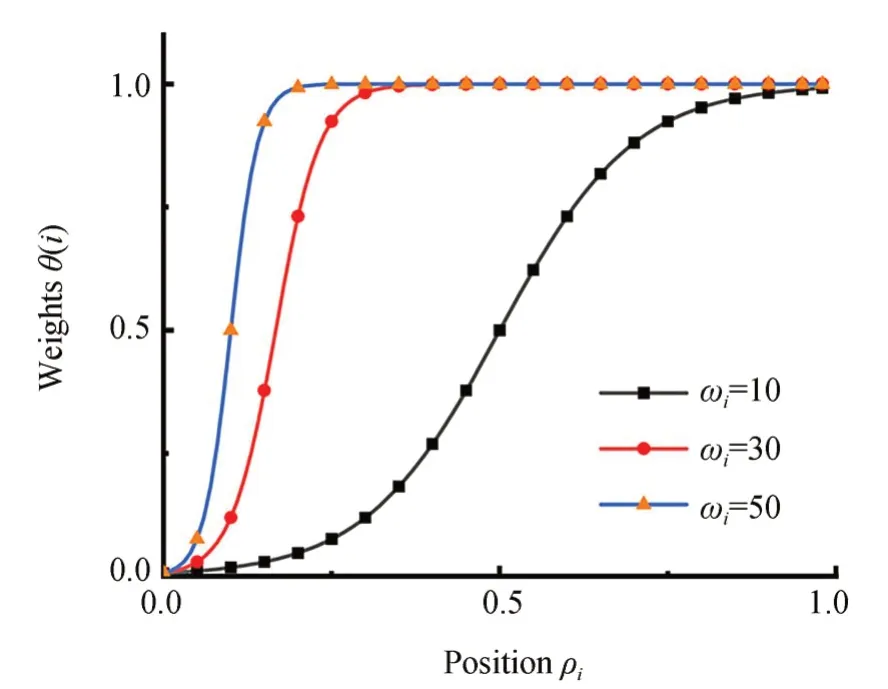
图4 不同参数值的改进Sigmoid函数Fig.4 Improved sigmoid function curves for different parameter values

式中：ρi为参与本次迭代配准的Npo个有序点对中，第i个点对所处位置i/Npo；ωi∈[10，upperi]为与配准误差相关的参数，upperi为其可变上界。

计算本次迭代的均方误差e，参数ωi的上界upperi定义为：

其中，ei′为上一次迭代的配准均方误差。

随着迭代次数的增加，相邻迭代的配准误差变化不断变小，ωi参数取值逐渐变大，即随着迭代过程的不断深入，更多的点对将被分配较高的权重。

3.2.2 配准参数求解

奇异值分解（SVD）可用于两组具有对应关系的点云集合的变换参数求解，其核心思想是构建使所有点对误差平方和达到极小的最小二乘问题：

首先定义两点云集合的质心：

进而最小二乘表达式表述为：

其中：x′i=xi-xc，y′i=yi-yc，最小二乘表达式（14）求解转换成两个表达式的最小化问题。通过前者求解出的旋转矩阵R，令后者表达式为零可求得平移矩阵t。

对矩阵H进行奇异值分解：

当R=VUT时tr(RH)取最大，同时t亦可求得。由式（18）可知，平衡权重θi在奇异值分解中影响正定矩阵U和V的计算值，进而影响到配准参数的求解。通过引入平衡权重前后的对比，如图5所示，可以看出，对于单次迭代，引入平衡权重后的配准效果与理想效果的契合度更高。

图5 Top3-Bun315配准效果截面图Fig.5 Cross-sectional view of Top3-Bun315 registration effect

3.2.3 算法实现

对于不同视角获取的具有重叠部分的点云配准工作，给定初始变换M0(R0，t0)，预设参数λ，改进的配准算法主要归纳为如下步骤：

（1）计算初始重叠率ξ0，使用改进均匀降采样算法对待配准点云进行降采样，获得参与迭代计算的初始源点云X和目标点云Y；

（2）对于第k次迭代，基于最近原则建立待配准点云间的点对关系，计算所有点对的距离并按大小升序排列：

（3）根据建立的点对关系，计算重叠率ξk和源点云X中表示重叠区域的子点集Pk：

式中：ξ∈[ξmin，1]，Pk=ξkX。

（4）使用基于误差权重的最小化目标函数，更新刚体变换关系：

其中，pi∈Pk。

对步骤（2）到步骤（4）进行迭代，当满足迭代停止条件，即迭代次数大于设定阈值或配准均方误差无明显变化，可输出最佳的刚体变换参数M(R，t)。算法需要已知待配准点云的初始重叠率ξ0，在初始配准位姿较好的情况下，可以通过最小包围盒算法进行估计。步骤（2）中点对关系的建立采用基于k-dtree的检索算法实现。对算法建立的最小化目标函数采用SVD进行求解，得出配准所需的最佳刚性变换。

4 实验与分析

为测试算法的性能，本文基于斯坦福大学图形实验室公开的Bunny数据集，设计了不同重叠度的配准实验和噪声实验，以检验本文算法对点云部分重叠配准工作的适用性和对噪声的鲁棒性，并与常用的ICP，Tr-ICP以及结合裁剪配准理论的AA-ICP配准算法进行对比。最后将本文算法应用到曲轴的三维点云重建任务上，测试其在工业零件三维重建上的实际应用能力。实验硬件平台为Windows10操作系统AMD Ryzen 3 1200 CPU@3.10 GHz，16 GB RAM的计算机，软件平台为Visual Studio 2017，算法采用C++结合点云库PCL 1.9.0实现。

4.1 斯坦福点云配准对比实验

为验证本文算法对点云部分重叠配准工作的适用性，本文设计了4组具有不同重叠率的点云配准实验，蓝色为源点云，红色为目标点云，点云之间只存在刚性变换，分组情况及基本信息如表2所示。为保证配准精度，减少耗时，所有数据集均采用本文降采样算法均匀采样至8 000～12 000点，取标准差增益系数ω=5。配准效果如图6所示（彩图见期刊电子版）。

表2 配准实验基本信息Tab.2 Basic information of registration experiment

图6 Bunny配准效果示意图Fig.6 Schematic diagram of Bunny registration result

由配准效果图可知，经典ICP算法对较低重叠率的配准工作表现出较差的适应性，而基于裁剪配准理论的本文算法以及其他对比算法，均能较好的完成配准任务。为进一步对比算法的性能，采用点对均方根误差（RMSE）作为精度评价指标，并统计各算法的RMSE及配准时间于表3和图7。

由表3可知，本文算法在精度方面均优于其他对比算法。Tr-ICP与结合裁剪配准理论的AA-ICP由于并未考量参与配准点对的有效性，故在配准精度上不及本文算法。同时，图7可直观地看出，在低重叠度情况下，本文算法较其他对比算法，精度提升更大。本文算法误差在重叠度45%的配准上，较Tr-ICP降低了约34%，较AA-ICP降低了约27%。在重叠度90%的配准上，较Tr-ICP降低了约20%，较AA-ICP降低了约16%。其部分原因可能为算法在低重叠的配准上，对点对的有效性更为敏感。高重叠度的配准，仅剔除了少量点对，而低重叠度的配准剔除了大量的离群值，少量的配准点对中，无效点对带来的影响被进一步扩大。本文算法基于有效点对的分布特性，对无效点对进行了抑制，故而在精度方面具有更好的表现。

图7 不同算法的RMSE和配准时间折线图Fig.7 RMSE and registration time for different algorithms

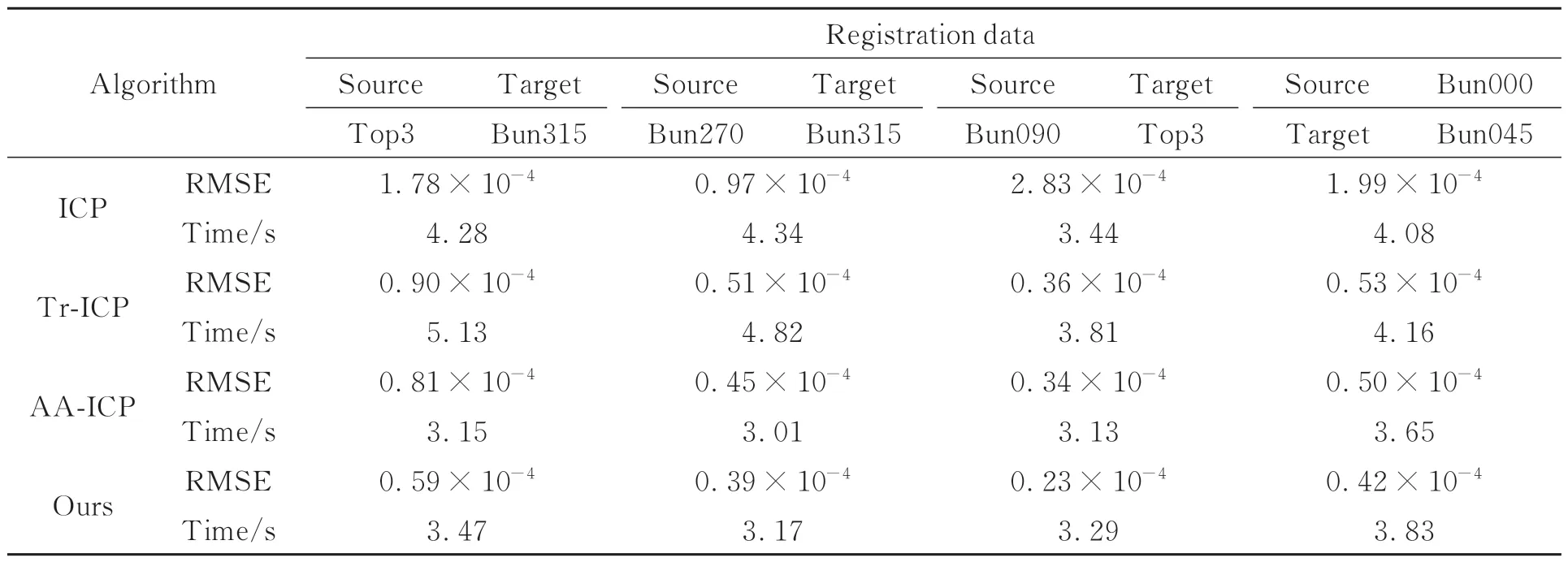
表3 不同算法的RMSE和配准时间Tab.3 RMSE and registration time for different algorithms

在配准效率方面，本文算法整体优于传统ICP和Tr-ICP算法。结合裁剪配准理论的AAICP采用粗配准提供的初始重叠率作为整个迭代过程的全局值，并未在迭代过程对其进行修正，同时基于Anderson加速原理对迭代过程进行了加速，因此在耗时上优于本文算法。本文及Tr-ICP算法耗时主要受主程序迭代和重叠度修正的影响，结合3.3.2小节相关论述，本文算法每次迭代的效果更为优质，算法更易收敛，因此效率较Tr-ICP有较大提升。在重叠度45%的配准上，配准耗时较Tr-ICP节省了约32%。在重叠度90%的配准上，较Tr-ICP节省了约8%。本文算法亦可在有需要时，取消对重叠度的修正，以获取更快的配准速度。

为进一步测试算法对重叠度的最低适应程度，在上文第1组实验基础上，对Bun270重叠部分点云进行裁剪，间隔差异为5%，细化了5组重叠度实验。本文算法配准效果如图8所示，各算法配准RMSE由表4统计，其中“-”表示配准失败，此时配准误差数值并不具备参考价值。

结合图8和表4知，本文算法在重叠率为25%时，仍有较好的配准效果，在重叠率为20%时配准失败。其他对比算法在重叠率为25%时，就已出现配准失败的情况，甚至ICP算法在低重叠率实验中，一直呈现错误的结果。一方面，重叠率的降低意味着要剔除更多被认为是离群值的匹配点对，保留距离较小的配准点对，而距离较小的点对更有可能是错误匹配点对，配准对剩下点对的有效性变得愈发敏感。另一方面，低重叠率配准对初始位姿的依赖性更高，若不能提供良好的初值，配准效果受到的影响更大。本文算法考虑了配准点对中无效点对的影响并进行了优化，在低重叠率的配准中，整体优于对比算法，在初始位姿良好情况下，能完成重叠度为25%的配准工作。

图8 不同重叠率的配准效果Fig.8 Registration results with different overlap rate

表4 不同算法的RMSETab.4 RMSE for different algorithms

4.2 噪声实验

在采集实体点云时，常常受到扫描位姿以及光照等环境因素的影响，导致点云夹杂着较多噪声点。为测试本文算法对噪声的鲁棒性，在4.1节第二组点云配准任务基础上，在两点云的最小包围立方盒内增添不同层级（N=1 000～5 000）的均匀噪声。使用本文降采样方法进行预处理，本文算法配准效果如图9所示。其他对比算法配准参数由表5统计，并绘制相关点线图如图10。

图9 不同层次噪声下本文算法配准效果Fig.9 Registration effect of the algorithm in this paper with different levels of noise

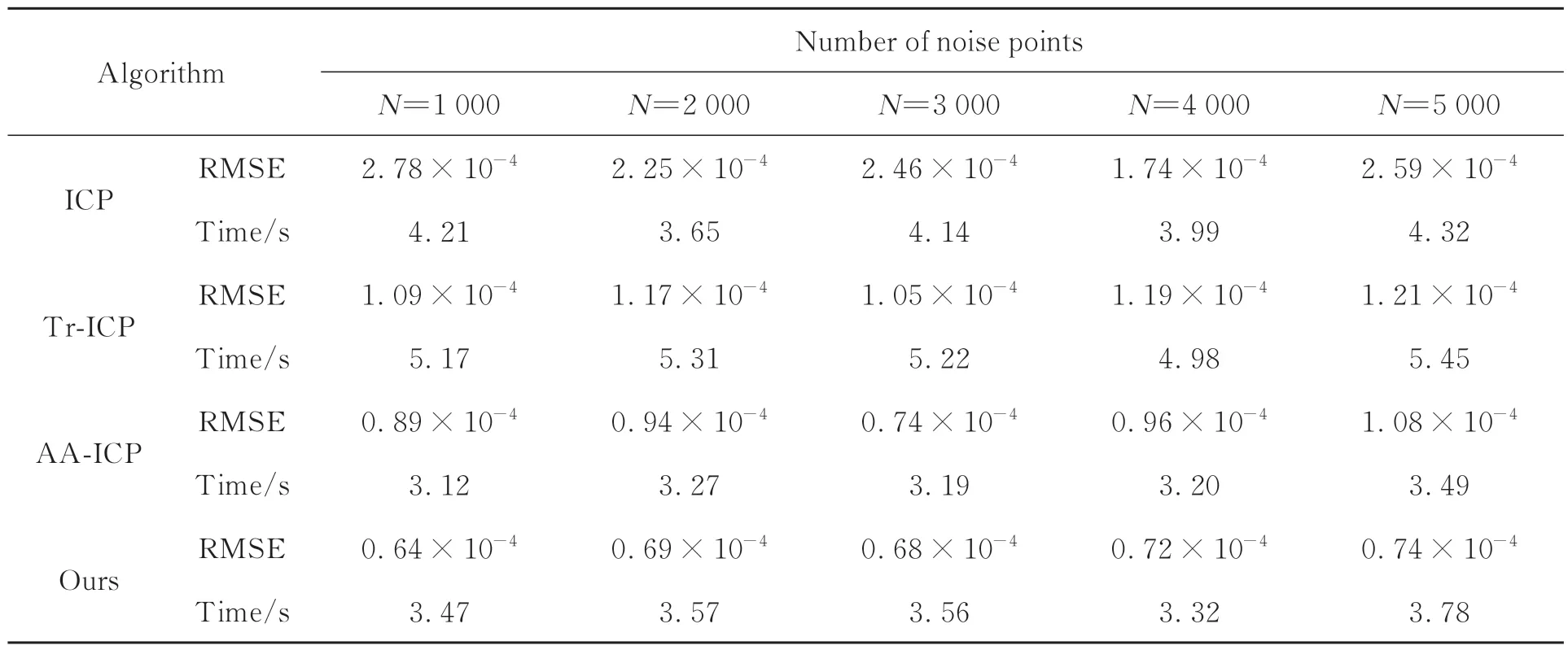
表5 不同层级噪声下各算法的RMSE和配准时间Tab.5 RMSE and registration time of each algorithm under different levels of noise

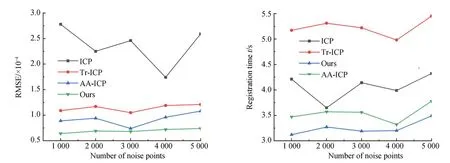
图10 不同层级噪声下，各算法的RMSE和配准时间折线图Fig.10 Line chart of RMSE and registration time of each algorithm under different levels of noise

均匀噪声在视觉上表现为靠近主体点云或远离主体点云，但在点云配准的最近邻搜索时，噪声点多与另一片点云的噪声点匹配且距离较小，给配准工作带来一定困难。由图9可知，本文算法在改进均匀降采样的配合下，对不同层级噪声均有较好的鲁棒性，并结合表5可知，本文算法在配准精度上明显优于其他对比算法。如图10所示，在配准精度方面，ICP算法即使采用了降采样，但仍受到噪声点与噪声点配准的影响，配准误差较大。由于本文采用的是基于体素网格划分的均匀降采样，对于不同层级的噪声，在采样过后点云外围存留的噪声点数量差异并不大，故在配准误差上，本文算法及其他两种对比算法的波动并不大。又由于本文算法考量了距离较小的配准点对中存在的无效点对，因此配准精度优于其他算法。

除上述噪声情况，点云配准工作还可能面临着由大量游离在点云主体表面的噪声点带来的配准困难。为验证本文算法对该类噪声的鲁棒性，对本小节的配准任务引入高斯噪声，在两片点云原有基础上，增添服从高斯分布g～N(μ，σ2)的噪声点。该噪声点为原始点云中已有点的偏移，设置参数μ=0，σ=0.002，通过实验与其他算法比对，配准结果如表6所示。

表6 带高斯噪声时不同算法的RMSE和配准时间Tab.6 RMSE and time of different algorithms with gaussian noise

结合表中数据并与均匀噪声实验对比，可见在引入高斯噪声情况下，各算法的配准误差均有一定程度的增大。其原因可能为，游离于点云主体表面的高斯噪声更难与真实点云区分，经过采样后的点云比真实点云更离散，匹配点对距离整体偏大，导致配准误差计算值更大。在高斯噪声的影响下，本文算法仍具有较好的配准表现，配准误差较Tr-ICP减少了约25.3%，较AA-ICP减少了约29.7%。通过实验比对，总结之，本文算法在精度和效率上较对比算法更有优势，同时对噪声也有较好的鲁棒性。

4.3 曲轴点云配准实验

为验证本文算法在工业零件三维点云重建任务中的实际应用能力，采用单缸曲轴作为点云扫描对象，使用不同算法进行配准实验并对比分析。曲轴点云数据由微软Kinect传感器于不同视角下获取。为重建出曲轴完整形貌，通过旋转曲轴于合适角度采集4片点云，对具有重叠部分的相邻两帧点云使用本文算法进行配准融合，得到最终用于实验配准的两片点云，如图11。实验单片点云体量超过10万，重叠度约40%，具有较多噪声点。曲轴点云已使用主成分分析法［2］进行粗配准，结合本文降采样方法，对不同算法的曲轴配准效果进行对比，其视觉效果如图12所示，配准误差及耗时统计于表7。

图11 实验环境及待配准曲轴点云初始位姿Fig.11 Experimental environment and initial pose of the crankshaft point cloud to be registered

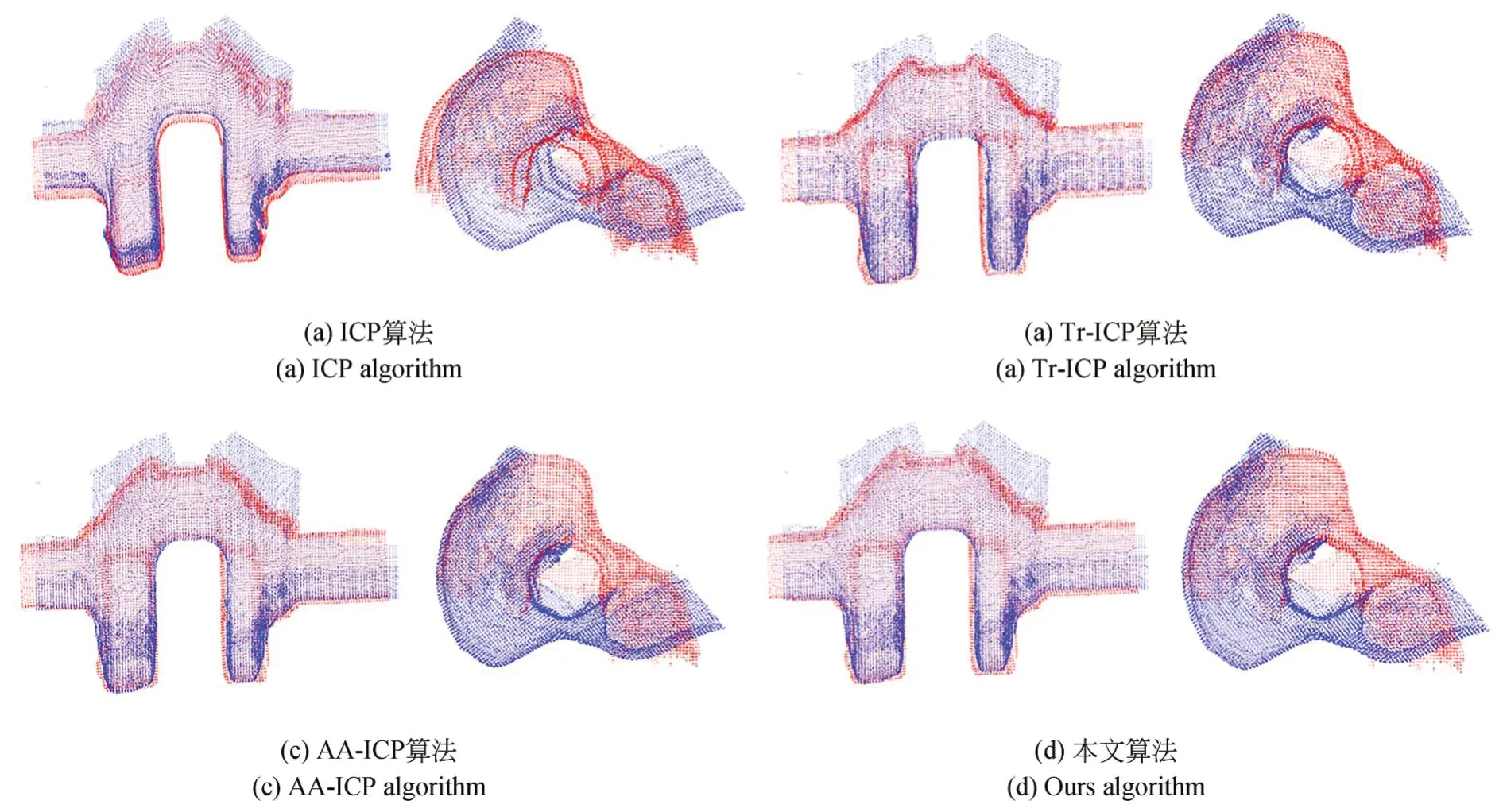
图12 曲轴点云配准结果Fig.12 Crankshaft point cloud registration results

从视觉上可以明显看出，经典ICP算法在配准曲轴点云时陷入了局部最优，Tr-ICP和AAICP算法虽然也达到了较好的整体配准效果，但在特征不明显的轴段处，其配准效果并不佳。而本文算法对于轴段及曲柄等局部的配准有着更高的吻合度，整体效果明显优于对比算法。结合表7中数据可知，本文算法在精度上明显高于经典ICP，Tr-ICP以及AA-ICP算法，配准RMSE较Tr-ICP算法减少了约34.1%，较AA-ICP减少了约29%，配准时间较Tr-ICP节省了约16.1%。总结之，本文算法在实际应用中，较对比算法有着明显的优势，可在工业零件的机检测任务中，用于实现零件的在线配准及重建。

表7 曲轴点云配准RMSE和配准时间Tab.7 Crankshaft registration RMSE and time

5 结论

本文提出基于匹配点对优化的点云模型配准算法，优化了配准任务前常进行的降采样策略，选用体素单元内由标准差增益系数所确定区间的中值点作为采样点，避免非均匀采样可能导致过多采样到非重叠部分问题的同时，提高了采样算法的抗噪声能力。针对Tr-ICP算法未能对存在距离较小的错误电对进行处理的问题，提出基于Sigmoid函数的点对平衡权重对算法进行优化，抑制距离较小的错误点对给配准工作带来的影响，以实现点云的精确配准。实验结果证明：本文算法在不同重叠度公开数据集、大量噪声点云以及实际工业零件点云的配准工作中均有良好的表现。相较于经典ICP，Tr-ICP以及AA-ICP算法，本文算法有着更高的配准精度，相较于传统算法，配准耗时更少。在曲轴三维点云重建实验中，本文算法相对于Tr-ICP算法，误差减少了约34.1%，较AA-ICP误差减少了约29%，配准时间较Tr-ICP节省了约16.1%。但同经典ICP及大部分改良算法一样，本文算法仍依赖于较好的初始配准位姿，因此未来需要就算法对初始配准位姿的鲁棒性作进一步探究。