数控机床在机测量系统最佳测量区确定方法

张双双， 杨洪涛*， 马 群， 李 莉

（1.安徽理工大学 机械工程学院，安徽 淮南 232001；2.安徽理工大学 安徽省矿山智能装备与技术重点实验室，安徽 淮南 232001）

1 引言

数控机床在机测量系统（简称在机测量系统）由机床和测头组成，其测量误差来源于机床几何误差、测量系统误差、测头误差等，受空间测量位置、测量速度、温度等因素的影响［1-4］，在整个测量空间内误差分布复杂且受到不同速度和空间位置等因素的影响，误差之间相互抵消或者加强，在不同测量位置下，测量误差分布规律存在差异。所以，测量误差在空间内存在着最大测量误差最小的区域（最佳测量区）［5］，将被测工件放置在该区域进行测量，可以实现低精度仪器高精度测量。

对于最佳测量区，国内外学者开展了相关研究，郑大腾等［6］针对关节臂测量机构建了最佳测量区的数学模型，并验证了其存在性。秦自瑞等［7］对测量机的圆编码器测角误差进行仿真分析，将测量空间划分成多个误差小空间并验证划分正确性。胡毅等［8］采用蚁群算法求解关节臂坐标测量机测量空间的最佳测量区，分析关节臂编码器零位和角度误差对测量机空间误差的影响情况，并采用粒子群算法验证最佳测量区的实用化。上述学者所研究的最佳测量区多数针对关节臂测量机，由于机床在机测量系统的误差源更多、传递关系更复杂，不同空间位置下误差有所差异，测量空间内误差分布规律非常复杂［9］，上述算法难以满足数控机床在机测量系统最佳区域确定要求。李莉［10］利用SA-GA算法求解数控机床在机测量系统点和线测量的最佳测量区。张宇［11］采用标准环规为测量对象，建立了空间误差和最佳测量区求解模型，应用BAS-PSO算法求解面向圆面测量的最佳测量区。目前在机测量系统测量对象基本上由点、线、面、球核心要素组成，其中球是最复杂的核心要素。上述面向对象的最佳测量区确定方法尚未针对球测量对象，同一个在机测量系统面向不同测量对象的最佳测量区域是不同的，而且面向不同被测对象的最佳测量区确定方法也不同，研究成果缺乏普适性。最佳测量区确定属于多维寻优问题，本文拟以球作为测量对象，采用基于布谷鸟搜索差分进化的混合优化算法（Differential Evolution Cuckoo Search，DE-CS），研究适合不同核心要素测量、具有普适性的数控机床在机测量系统最佳测量区确定方法，并利用实验进行验证。

2 在机测量系统误差分析与建模

2.1 在机测量系统测量原理

本文研究的在机测量系统由机床本体和测头组成，如图1所示。被测工件安装在XY工作台上进行X，Y向运动，测头安装在Z向主轴上沿Z向运动，被测点三维坐标由测头触发机床坐标测量系统测量与显示。为了提高球体测量精度，本文采取六点测球法［12］，在两个不同Z向高度的圆截面上共选取6个特征采样点，通过测量软件读取其空间位置坐标，采用最小二乘法反解出球径和球心。

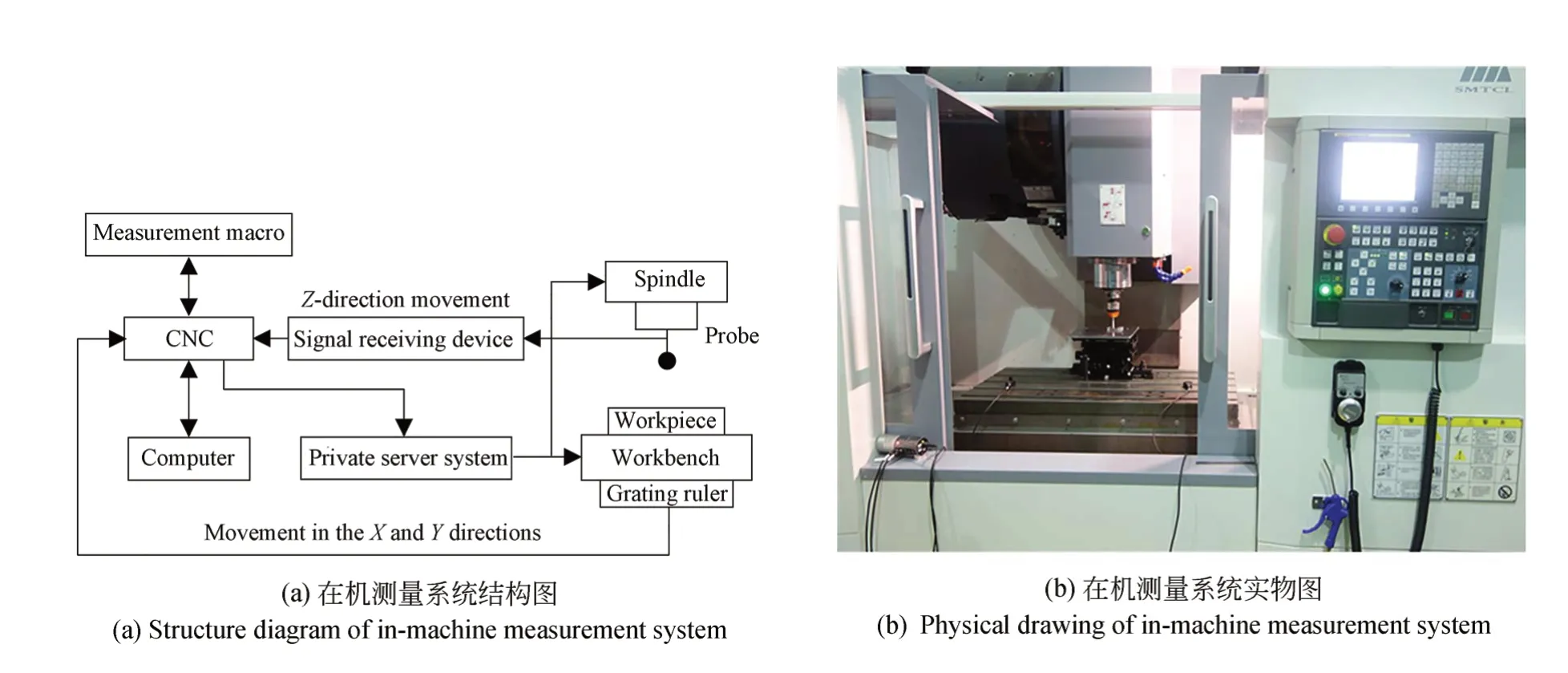
图1 数控机床在机测量系统Fig.1 CNC machine tool in machine measurement system

在机测量系统的测量误差主要来源于机床本体几何误差和测头误差。工作台沿各方向导轨进行测量运动时，受机床制造、安装误差及环境因素的影响，机床本体会产生21项误差（18项位置相关几何误差和3项垂直度误差），以及热误差、运动误差等。这些误差受空间位置、运行速度等因素影响，呈现复杂规律变化。测头系统的误差主要可以分为预行程误差、测量方向性误差、测头的安装定位误差等，目前本文所研究的机床测头触测方向、速度暂时无法调节，因此本文暂不予考虑。为了有效提高在机测量系统的测量精度，可以将工件放入确定的最佳测量区内，从而能够实现低精度在机测量系统的高精度测量。要确定在机测量系统最佳测量区，必须建立各单项几何误差的精确预测模型，进而实现测量系统综合误差建模预测。

2.2 在机测量系统误差建模

2.2.1 单项误差建模

利用双频激光干涉仪和球杆仪对如图1所示在机测量系统的各单项误差进行测量与识别，根据现有实验条件，确定所取的测量空间范围为304.487 mm≤X≤504.487 mm，-229.042 mm≤Y≤-29.042 mm，-420.202 mm≤Z≤-220.202 mm。利用测量数据和BAS-BP神经网络进行单项误差建模，其中建立的X轴偏摆角误差εz(x)预测模型如式（1）所示，建模结果如图2所示，其中x(n)为坐标值，v(n)为该方向测量速度值。同理，可得到三轴机床其他单项几何误差预测模型。

图2 X轴偏摆角误差拟合结果Fig.2 X-axis yaw angle error fitting results

2.2.2 综合误差建模

由于滚转角误差较小且对机床总体误差影响较小，本文忽略误差建模中的滚转角误差，因此利用多体系统理论建立的三轴机床的综合误差预测模型如式（2）所示［13］：

其中：δx(x)为X轴定位误差，δy(x)，δz(x)为X轴方向下Y，Z方向的直线度误差，εz(x)，εy(x)分 别 为 偏 摆 角 和 俯 仰 角 误 差；γx，y，γy，z，γx，z分 别是X，Y，Z三移动轴相互之间的垂直度误差，可利用球杆仪测量得到，分别为-74.5 μm/m，-131.7 μm/m，-65.7 μum/m。

2.2.3 标准球测量误差模型

本文以标准球体作为较复杂的测量对象，通过测量包含各点综合误差Δx，Δy，Δz的球体6个特征点的三维坐标值，如图3所示，采用最小二乘法计算求解得到误差影响下的球心坐标和球径，并与标准球的标准球径对比，得到球体直径测量的误差模型如式（3）所示：

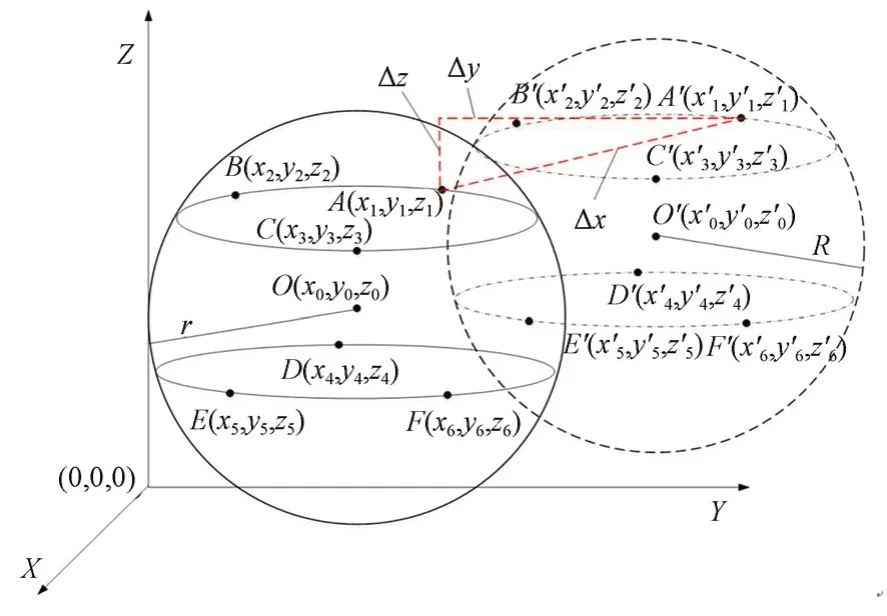
图3 球体测量误差模型图Fig.3 Sphere measurement error model diagram

其中：Δd为标准球的外直径测量误差，R为待测球的标准球径，r为误差影响下的新球径值。

3 基于DE-CS的最佳测量区确定方法

在机测量系统测量误差在整个测量空间内分布复杂，且受到不同速度和空间位置等因素的影响，误差之间相互抵消或者加强，因此测量误差在空间内存在着连续且大小不一的分布区域，该种区域是连续变化且有规律可寻的，其中最大测量误差相比较为最小的误差区域称作最佳测量区。

3.1 最佳测量区求解的函数模型

由于在机测量系统测量误差的影响因素和约束条件较多，为了方便研究多维寻优问题，首先需要解决的是建立最佳测量区的求解模型，如式（4）所示：

其中，下标LBmin和LBmax分别代表对应轴方向位置区域的下限和上限。以采样点坐标三维上、下限作为约束条件，转为有约束优化问题，使得特征点的坐标位置未超过划分的小空间区域。

由于函数模型（4）存在多个变量，影响因素较多且复杂，需要研究选用不同多维寻优算法来求解该多维模型，比较各算法求解的误差值大小，同时对比各算法性能，得到全局搜索能力最强、迭代速度最快的优化算法。

3.2 差分进化优化的布谷鸟算法

3.2.1 算法原理

（a） CS算法基本原理

布谷鸟算法（Cuckoo Search，CS），其工作机理主要是根据布谷鸟的寻窝寄生产卵行为和鸟类的莱维飞行。由于其具有参数少、不易陷于局部最优和鲁棒性强等特点，因此较为适用于优化问题。

①种群初始化，设置算法参数：鸟窝数量为N，发现概率pa，最大迭代次数为M，维度为D；

②选择适应度函数，并且针对鸟窝位置计算适应度值，得到最优鸟窝位置和最优解；

③利用莱维飞行对鸟窝位置进行更新，记录当前最优值；

④用随机数R作为鸟窝主人发现寄生蛋的概率，若R＞pa，则随机改变并更新鸟窝位置；

⑤若算法满足要求，输出期望值；否则返回②步骤继续运行。

（b） DE-CS算法基本原理

基于差分进化优化的布谷鸟算法是基于差分进化搜索的布谷鸟最优化算法［14-15］。基于适者生存的自然法则对种群中的个体进行淘汰选择、保留优良个体，使得差分进化得出的最优解成为布谷鸟算法的初始解，经过布谷鸟算法的迭代搜索，获得更优的鸟窝位置和目标解。该算法可以获得更好的全局搜索能力和更快的收敛能力。本文将利用该算法作为最佳测量区的确定方法，该算法流程图如图4所示。

图4 DE-CS算法流程图Fig.4 Flow chart of DE-CS algorithm

（c） DE-CS算法步骤

①生成初始种群，设置迭代次数M和发现概率pa，初始变异算子F0，交叉算子CR，在D维空间生成N个初始位置；

②对初始种群实行变异、交叉、选择操作，得到新种群用以替换原有种群，得到目标问题的最优解；

③以DE算法得到的全局最优位置作为布谷鸟搜索的初始种群，进行布谷鸟算法搜索操作，更新鸟窝位置，计算适应度值；

④将步骤③中得到的更新后的鸟窝位置计算适应度，与原有鸟窝匹配的适应度值比较，若更优则替换该鸟窝位置，记录当前最优位置和最优解；

⑤取随机数R∈[0，1]，若R＞pa，鸟窝主人发现寄生蛋，随机改变鸟窝位置；

⑥改变后的鸟窝位置计算适应度值，确定全局最优位置和最优解；

⑦进行判断操作，若是达到终止条件，则输出期望最优解；否则返回第③步重复搜索。

3.2.2 求解最佳测量区

（a）单种优化算法寻优结果对比

本文分别采用ACO，CS，DE，ABC，FA等基本最优化算法和混合优化算法（IA-PSO，QGACS，DE-CS）求解式（4）的误差最小值，算法参数设置如表1所示［16-17］。为了测试上述5种基本智能算法的性能，分别利用5种算法求解在机测量系统小立体空间范围（该区域后称选定小立体空间：304.783 mm≤X≤313.783 mm，-90.133 mm≤Y≤-81.133 mm，-288.019 mm≤Z≤-278.019 mm）内的面向球体测量的测量误差最大值的极小值。5种常用算法搜索迭代结果如图5（a）所示，4种基于CS的混合算法如5（b），重复运行50次结果对比如表2所示。

表1 5种算法参数设置Tab.1 Parameter settings of five algorithms

表2 5种算法50次测试结果对比Tab.2 Comparison of 50 test results of five algorithms （μm）

图5 算法搜索对比Fig.5 Comparison of algorithm search

由表2中的对比可知，DE，ABC，CS三者未陷入局部最优，但是相较而言CS算法运行50次后平均值最接近全局最优值，搜索时间最短，实时性好，综合寻优性能最优。因此有必要在CS算法的基础上，进行更深一步的优化，研究基于CS算法的混合智能算法。

（b） 三种基于CS算法改进的混合算法性能对比

本文提出3种基于CS算法优化的混合算法和基本的CS算法。其中3种优化的CS算法参数设置如表3所示［18］。将3种优化和基本的CS算法分别用于求解选定小立体空间的最大误差值，4种算法搜索迭代结果如图5（b）所示，重复运行50次结果对比如表4所示，可知DE-CS算法的性能要优于其他几种算法，能够很好地应用于最佳测量区确定。

表3 3种改进的CS算法参数设置Tab.3 Parameter Settings of three improved CS algorithms

表4 4种算法50次测试结果对比Tab.4 Comparison of 50 test results of the four algorithms

为了测试算法参数对寻优性能的影响，改变种群数量N、变异算子F0、交叉算子CR等参数，应用模型式（4）求解小立体空间的最大测量误差。DECS算法参数设置，其他参数不变：（1）粒子规模N=20，40，60，80，100；（2）初始变异算子F0=0.2，0.4，0.5，0.8，0.9；（3）交 叉 算 子CR=0.1，0.3，0.5，0.8，0.9，探 究 算 法 的 性 能最优，如表5所示。

表5 改变初始参数的算法测试结果Tab.5 Algorithm test results of changing initial parameters

（c） DE-CS算法参数测试性能对比

可知，针对DE-CS算法的参数确定为种群数量N=20、初始变异算子F0=0.8、交叉算子CR=0.9时，该算法收敛稳定性最好，全局搜索能力最优，因此可以作为在机测量机最佳测量区的确定方法。

4 最佳测量区验证实验

4.1 球体测量最佳测量区验证实验方案设计

为了验证上述面向球体测量的在机测量系统最佳测量区确定结果，现搭建如图6所示的实验装置。以沈阳机床厂生产的VMC850E型三轴机床和雷尼绍公司的Primo Radio Part Setter接触式工件测头组成的测量系统为对象，将标准球通过可调夹具安装在在机测量系统的三维工作台上，在用于测量机床几何误差的双频激光干涉仪的有效测量区域内，开展球体测量的最佳测量区验证实验。

图6 试验装置图Fig.6 Test device diagram

将球径为38.112 8 mm的标准球体放置于304.478 mm≤X≤475.783 mm，-145.133 mm≤Y≤-45.602 mm，-288.019 mm≤Z≤-226.056 mm的测量空间内，将上述测量空间划分成多个的小立体空间，调节可调三维工作台带动标准球体完成不同空间位置处的误差测量。将球体标准球径与测量值相比，得到不同立体球体的测量误差，其中具有较小测量误差的测量区域如图7所示。

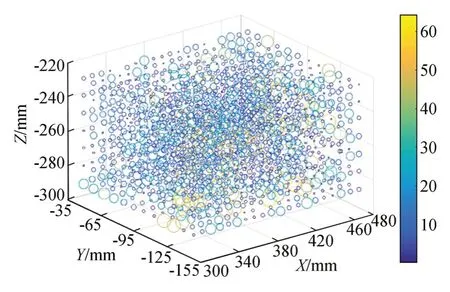
图7 球体测量的测量误差分布图Fig.7 Measurement error distribution diagram for sphere measurement

4.2 球体测量最佳测量区的确定

为对比利用DE-CS算法求解确定和实际测量得到的在机测量系统面向球体测量的最佳测量区的一致性，采用DE-CS算法，针对第2节建立的单项误差模型、综合误差模型、球体测量误差模型，进行全局搜索寻优。同样将上述测量空间划分成多个9 mm×9 mm×10 mm的小立体空间，进行搜索寻优计算得到球体测量的测量误差分布如表6所示。

从表6可知，在选定测量空间内430.783 mm≤X≤439.783 mm，-145.133 mm≤Y≤-136.133 mm，-268 mm≤Z≤-258 mm区域，球体实测最大测量误差最小值为3.1 μm，同样该区域利用DE-CS算法搜索求解的误差也为整个测量空间的测量误差最小值0.710 7 μm，从而可知利用本文研究的误差模型和DE-CS算法搜索求解可以确定在机测量系统面向球体的最佳测量区。其中两者方法确定误差最小值有差异是由于球体测量夹具等因素带来了附加误差。

表6 最大测量误差分布区域对比Tab.6 Comparison of maximum measurement error distribution regions

4.3 最佳测量区确定方法的普适性验证

为了验证上述最佳测量区确定方法的普适性，对于其他测量对象也具有同样的效果，本文按照同样的思路，分类建立面向点、面的测量误差模型，采用全局搜索的DE-CS优化方法计算确定面向点、面的选定区域内的最佳测量区位置，并利用参考文献［10］实际测量标定的在机测量系统最佳测量区结果进行对比，分别如表7～表8所示。由表可知，利用本文研究的DE-CS算法求解的最佳测量区与实测结果相符合，且与前期采用不同算法确定的最佳测量区重合，验证了本文研究的在机测量系统最佳测量区确定方法的正确性和普适性。

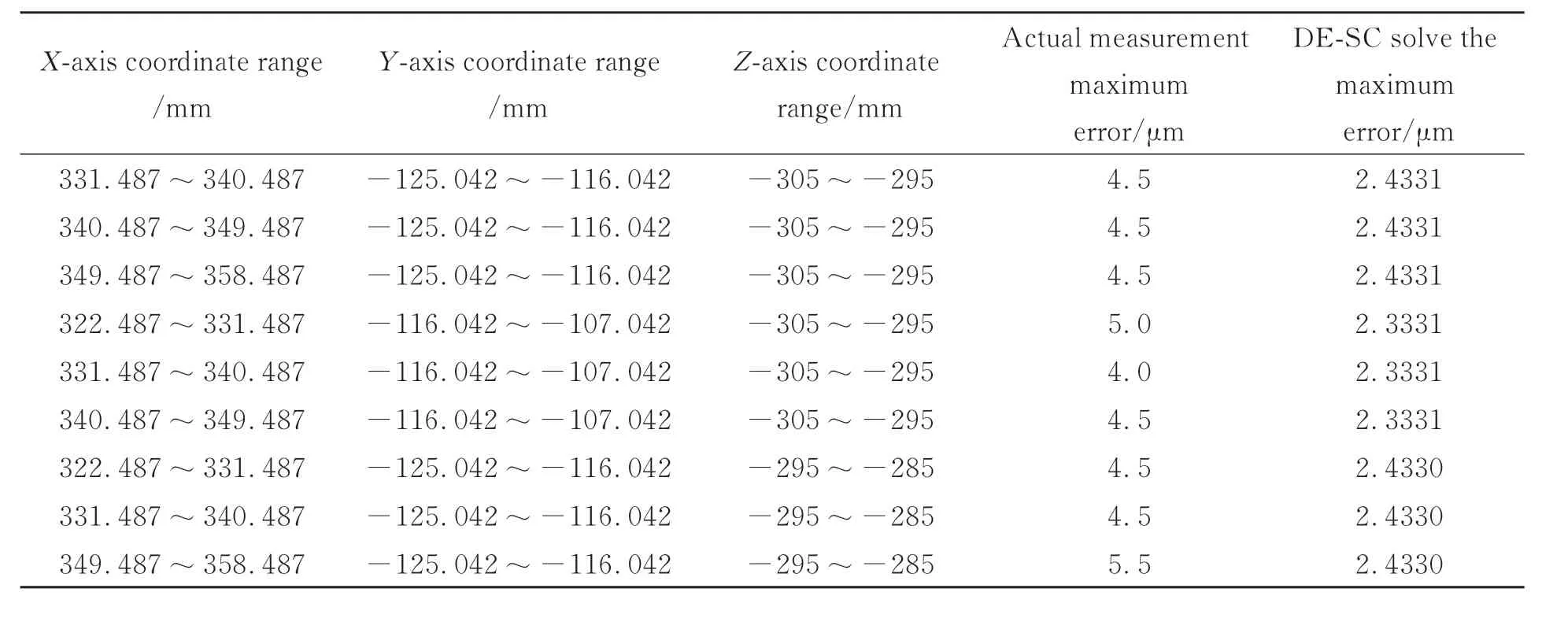
表7 点测量最佳测量区对比Tab.7 Comparison of optimal measurement areas for point measurement

表8 圆面测量最佳测量区对比Tab.8 Comparison of the best measurement areas for circular surface measurement

5 结论

（1）对于在机测量系统的误差来源进行了分析，采用激光干涉仪测量几何误差，利用BASBP神经网络建立了误差白化模型，并建立了综合误差和面向点、面、球的测量误差模型。

（2）研究了利用差分进化优化的布谷鸟算法（DE-CS），求解搜索空间内最大测量误差最小值，进而确定最佳测量区位置，并与其他算法进行比较，验证了其具有搜索能力最强、稳定性最佳等特点，并确定了该算法的最优初始参数。

（3）搭建了面向球测量的在机测量系统最佳测量区的试验装置，进行了最佳测量区的实际测量确定实验。利用上述方法搜索计算确定的面向球最佳测量区位置与实验测量确定的最佳测量区位置一致，最佳测量区为：430.783 mm≤X≤439.783 mm，-145.133 mm≤Y≤-136.133 mm，-268 mm≤Z≤-258 mm，实测最大误差最小值为3.1 μm，算法求解的误差也为整个测量空间的最小值0.710 7 μm，且可用于面向点、面等其他测量对象的最佳测量区确定，具有普适性，可用于确定在机测量系统的最佳测量区。