钢-混组合梁桥不同模型精度分析研究

肖鹏程

(中国电建集团贵阳勘测设计研究院有限公司城建设计院，湖北 武汉 430050)

近些年来，随着社会经济的不断发展，我国对交通基础设施建设的投入也加大，其中桥梁作为控制性工程建设越来越多，桥梁建设压力越来越大，随着钢混组合梁的广泛应用，桥梁建设压力得到缓解，尤其是在建设城市高架桥中应用颇多[1～2]。钢-混组合梁桥是钢主梁与混凝土桥面板之间通过剪力钉与现浇混凝土耦合形成整体共同受力的一种结构形式，既发挥了钢材的抗拉性能，又发挥了混凝土的抗压性能，具有两种材料优越的力学性能且易于施工[3～5]。针对钢-混凝土组合梁进行结构分析时，采用不同有限元模型分析对结构施工阶段和成桥阶段的应力以及位移等有很大的差异[6]。目前已有的研究成果大多仅仅采用单一的计算模型进行分析，而对不同模型的精度以及适用性鲜有研究[7]。为此分别采用组合梁施工联合截面和双主梁单元两种梁单元模型，分析了组合梁精细模型采用不同模型的计算差异，对比了在施工阶段和成桥阶段的应力、挠度等响应，从而得到一种更值得推荐的组合梁桥有限元计算分析方法，为实际工程提供借鉴。

1 组合梁模拟方法介绍

1.1 组合梁联合截面梁单元

组合梁联合截面主要是将钢材与混凝土两种不同材料之间看成紧密连接形成整体截面，忽略钢材与混凝土之间的相对滑动，所以在分析组合梁中钢梁与混凝土桥面板之间局部的滑动现象时，不能采用这种组合梁联合截面模拟方式。在分析组合梁结构时，首先基于等效刚度原则换算两种材料截面，然后依据此按照常规方法计算普通截面，对此进行力学性能分析。采用这种方法可以较为准确的模拟混凝土桥面板与和钢箱梁两种材料之间的连接作用，比较接近于钢混组合梁结构的受力特性。由于基于等效刚度原则将两种材料通过换算后等效成全截面，因此忽略了桥面板混凝土单独的收缩徐变效应。目前常通过折减混凝土的弹性模量的方法来分析桥面板的收缩徐变效益，但此方法计算误差较大，不适合精细化分析桥面板收缩徐变。

1.2 双主梁单元

双主梁单元即分别建立桥面板梁单元和钢梁单元，然后将两者通过弹性连接的刚接模拟剪力钉的作用连接主梁。但是桥面板轴线与钢箱梁轴线在实际工程中有着一定的距离，而两种不同单元产生的轴力相对组合梁轴心会形成弯矩，因此如果忽略钢箱梁与桥面板之间的相对位置，将两种材料单元看成同一节点连接的，就会致使结构计算分析出现较大的误差甚至完全错误。基于此问题，在钢梁单元和桥面板单元之间采用刚臂单元来连接，刚臂长度依据钢梁与桥面板之间的相对位置而定。但是此方式模拟组合梁仍旧有着很大的局限性，因为刚臂忽略了单元中间部分的连接，仅仅连接了钢梁与桥面板单元接近的两端节点，导致了单元内部的变形不一致，使得组合梁结构力学特性与实际工程中结构有着一定的误差，所以如果选择此单元模型分析模拟时，必须将单元长度划分精细，从而在一定程度上减小误差。

1.3 梁+板双单元

梁+板双单元模型也类似于双主梁单元模拟方式，其中钢箱梁使用梁单元进行模拟，桥面板则使用板壳单元进行模拟，两者同样采用刚臂进行连接。这种方法不仅有着双主梁单元模型的优点，而且还运用了更加精细化的板壳单元模拟桥面板，可以比较准确的反映桥面板剪力滞效应、偏载效应等空间受力特点，是一种较为准确的有限元模拟方法。然而在板壳单元中较难考虑钢筋、预应力荷载等因素，因此这种方法也存在一定的局限性。

2 依托工程概况

由于依托工程为在建项目，故全文用某在建多跨钢混组合梁桥代替，桥梁全长为360 m，跨径组合为4 m×90 m，桥宽17.5 m，双向四车道。组合梁采用预制桥面板，桥面板间通过湿接缝联系。为控制负弯矩区桥面板应力，通过支座预位移削减混凝土应力。桥面板采用C50混凝土，钢梁采用Q355C钢材。

3 组合梁计算模型建立

3.1 组合梁联合截面单元模型

通过软件中的施工联合截面来模拟桥面板与钢箱梁的连接作用，通过建立单梁模型来模拟组合梁桥结构，将主梁单元精细划分为1 m，全模型共包含360个单元。

3.2 双主梁单元模型

分别建立桥面板梁单元和钢梁单元，然后将两者通过软件中的刚性连接的刚性进行连接。通过有限元软件进行建模时，可选择软件中的截面偏心功能来模拟钢箱梁质心与桥面板质心的距离，主梁单元精细划分为1 m，全模型共包含720个单元。

3.3 梁+板双单元模型

结合钢混组合梁桥的受力特点，梁+板单元主要是通过建立梁单元模拟桥梁的钢箱梁，同时结合混凝土桥面板结构的壳体特点，建立板壳单元模拟桥面板。梁单元和板壳单元通过偏心共结点的方法进行连接，有限元软件在分析时，两种单元的质心通过刚臂建立连接，以确保它们二者受力状态一致。为合理布置桥面板中的预应力钢束，单独建立没有自重与刚度的虚拟梁单元，在虚拟梁单元中施加预应力并通过共节点方式传递至桥面板中。

4 不同模型受力特性分析

为避免桥面板铺装完毕后墩顶处负弯矩区混凝土开裂，预先将中间的支座升高，待钢箱梁与混凝土桥面板通过湿接缝结合成组合结构后再回落支座以储备预压力。为比较三种不同的有限元模型计算精度的差异性，将对比分析钢箱梁架设后各施工阶段中钢箱梁和桥面板的应力、位移及成桥后桥面板的应力。钢箱梁架设完毕后的施工阶段如表1所示。

表1 钢箱梁架设后各施工阶段

4.1 钢箱梁应力分析

根据midas Civil分析不同有限元模型，得到三种模型中边跨跨中和次中点位置处的钢箱梁上下翼缘板在各施工阶段的应力值，如图1和图2所示。

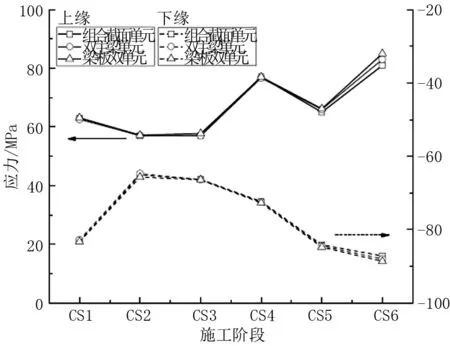
图1 边跨跨中钢箱梁应力图

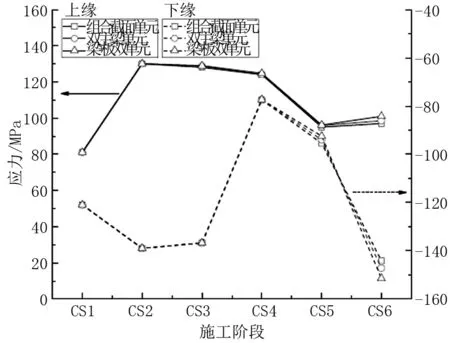
图2 次中跨支点处钢箱梁应力图

由图1和图2可知，在钢箱梁和桥面板混凝土形成整体受力前的施工阶段中，采组合梁截面单元模型、双主梁单元模型和梁+板单元模型所得到的钢箱梁上下缘应力接近，但是通过钢箱梁剪力钉和湿接缝的连接形成整体后，模型精度的差异性渐渐显示出来，钢箱梁上下缘的最大应力均为梁+板双单元模型所得到的，其中边跨跨中和次中跨支点钢箱梁上缘最大应力分别为83.7 MPa和101.5 MPa；而组合截面单元模型得到的钢箱梁应力最小，其中边跨跨中和次中跨支点钢箱梁上缘最小应力分别为80.7 MPa和97.9 MPa；因此相对于组合梁截面单元模型的相对误差均在5%以内。

4.2 桥面板应力分析

针对各施工阶段桥面板应力进行分析，分别得到三种模型在各个施工阶段的边跨跨中和次中跨支点位置处的桥面板混凝土上翼缘应力值，如图3和图4所示应力。特别注意的是梁+板双单元模型的应力取值为混凝土桥面板中心线上的应力，避开了应力集中区域。

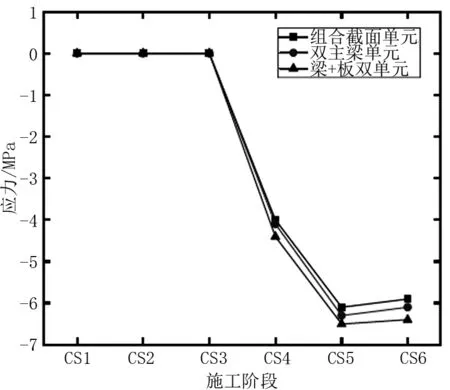
图3 边跨跨中混凝土上缘应力图

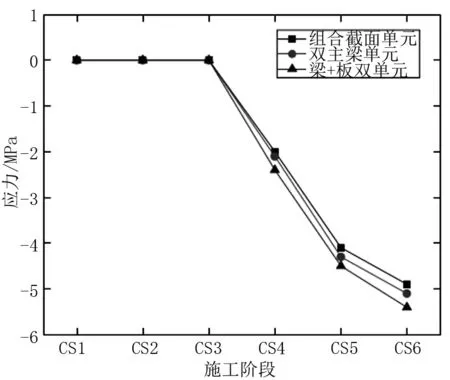
图4 次中跨支点混凝土上缘应力图

由图3和图4可看出，三种单元模型均能相对正确的模拟出桥面板混凝土的应力状态，同样待混凝土湿接缝与钢箱梁剪力钉连接成整体结构前，混凝土桥面板是不参与整个体系受力的，等到桥面板与钢箱梁连接成整体同时解除支座预顶后，三种单元模型中桥面板的应力值渐渐显示出差异性。总的来说，采用梁+板单元模型计算得出的桥面板应力值相较于其他两种模型偏大，其中边跨跨中和次中跨支点混凝土上缘压应力最大分别为6.5 MPa和5.3 MPa，最小分别为6.2 MPa和5.1 MPa，但相对误差均在5%以内。

4.3 成桥运营阶段挠度分析

针对成桥运营阶段主梁各位置挠度进行分析，分别得到三种不同模型在各个位置的位移值。如图5所示。

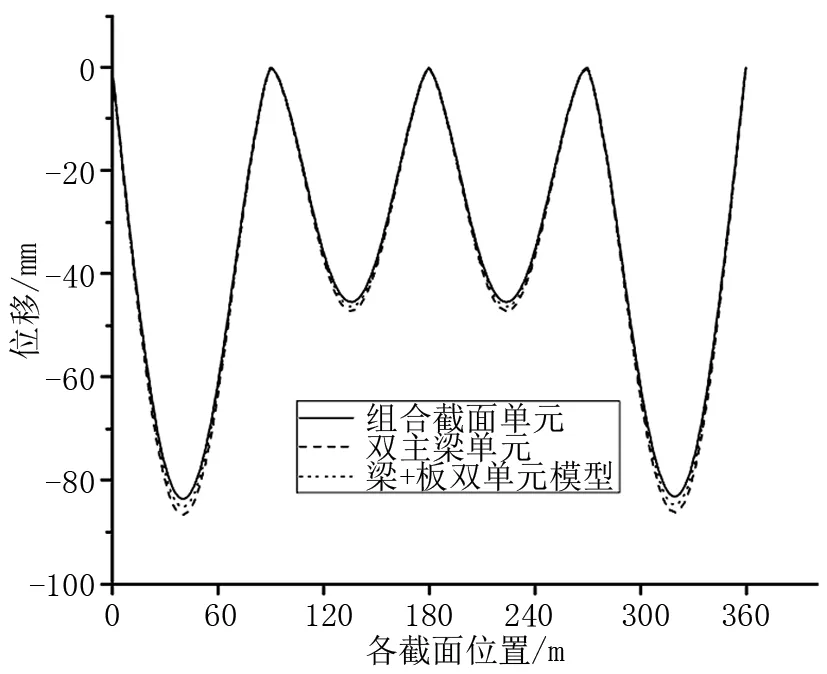
图5 成桥运营阶段截面位移图

根据图5可知，三种有限元模型计算得出的结构位移曲线整体趋势接近，其中梁+板单元模型计算得到的结构位移值比其他模型大，最大下挠达到了86.7 mm，但相对误差均不超过3%。

5 结 论

(1)在各施工阶段中，三种单元模型得到的钢箱梁上下翼缘应力和桥面板上缘应力的接近一致，待混凝土湿接缝与钢箱梁剪力钉连接成整体后，三种模型显示出差异性，其中梁+板双单元模型计算结果偏大，但相对误差不超过5%。

(2)成桥运营阶段，三种模型模拟方式得到的结构位移曲线整体趋势接近，但梁+板单元模型位移计算结果相较于其他两种模型偏大，相对误差为3%左右。

(3)采用梁+板双单元模型计算多跨钢混组合梁，能够较为精确的模拟结构实际受力情况。