基于GTD模型的多视角多频带ISAR融合成像

朱晓秀, 刘利民, 胡文华, 郭宝锋, 史 林, 朱瀚神

(1. 陆军工程大学石家庄校区电子与光学工程系, 河北 石家庄 050003;2. 中国人民解放军32398部队, 北京 100192)

0 引 言

对于传统的单基逆合成孔径雷达(inverse synthetic aperture radar, ISAR)成像系统[1-5]而言,图像的距离分辨率和方位分辨率分别受雷达的发射信号带宽和观测累积角度的限制,因而无法突破其理论分辨率[6-10]。为提高二维分辨率,多视角多频带ISAR融合成像技术利用工作在不同频段的多部雷达从不同角度观测目标,通过对观测回波进行融合处理,等效得到一个更大带宽和更大视角的回波[11-13]。该方法打破了单基地雷达成像分辨率的约束,可同时提高ISAR成像的二维分辨率。

多视角多频带ISAR融合成像方法主要基于谱估计和基于稀疏表示两大类。谱估计类融合成像方法[14-17]将ISAR融合成像模型转化为二维指数和模型,并分解为两个一维矢量,利用谱估计方法分别估计参数。此类方法在散射点个数精确已知的情况下可较好地实现信号融合,但实际情况下散射点个数一般很难准确估计,而且还存在散射点的二维坐标配对问题,影响了算法性能。稀疏表示类融合成像方法[18-20]利用成像场景网格化处理模拟散射点可能出现的位置,将ISAR融合成像问题转化为信号的稀疏表示问题,利用稀疏重构方法进行求解。此类方法无需估计散射点个数,也不涉及散射点坐标配对问题,算法性能优于谱估计类方法。

在高频区,目标的电磁散射可近似等效为多个独立散射点的后向电磁散射之和。在窄带小角度观测条件下,散射点的散射系数可认为是常数,近似为理想散射点模型。文献[21]利用理想散射点模型建立ISAR成像回波模型,提出了一种基于稀疏表示的多雷达信号二维融合成像方法,利用基追踪算法求解稀疏表示问题,得到的融合成像结果要优于谱估计方法。然而,在宽带小角度观测条件下,散射点的散射系数是随频率变化而变化的。为更准确地反映目标的散射特性,文献[22]提出了一种基于几何绕射理论(geometrical theory of diffraction, GTD)模型的多雷达信号二维融合方法,将多雷达信号的二维融合问题转化为稀疏表示问题,利用正则化方法能较好地估计目标的散射参数。然而,在建立多视角多频带ISAR融合成像的稀疏表示模型时,需要将二维回波数据矢量化处理,此时涉及到大规模数据重构,利用正则化方法迭代求解时运算量大,耗时较长,而且需要人工调整正则参数,影响了算法性能。

基于此,本文提出一种新的基于GTD模型的多视角多频带ISAR融合成像方法,在利用GTD模型建立ISAR成像回波模型的基础上,采用矢量化处理,将多视角多频带ISAR融合成像问题转化为信号稀疏重构问题。为减少运算复杂度,利用正交匹配追踪(orthogonal matching pursuit, OMP)算法实现稀疏重构,在保证成像质量的同时提高融合成像效率,仿真实验验证了算法的有效性。

1 单站ISAR成像回波模型

假设雷达发射LFM信号,在成像时间Ta内共发射N个脉冲,脉冲重复时间为Tr,tn=nTr为慢时间,其中n=0,1,…,N-1。若目标共有P个独立散射点,经解线频调处理后,基于理想散射点模型目标回波可写为

(1)

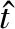
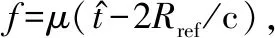
(2)

1.1 GTD回波模型

在宽带成像时,散射点的散射系数随频率变化而变化,此时利用理想散射点模型不能准确描述目标的散射特性。为考虑散射系数随频率变化的特性,引入频率依赖因子αp,在式(2)的基础上,利用GTD模型[23]构建目标回波,可表示为

(3)

式中:f0为频带的起始频率;αp为散射点p的频率依赖因子。在GTD模型中,不同的αp可表征不同的散射点类型,典型的散射点类型及对应的频率依赖因子如表1所示[24]。

表1 典型的散射点类型及对应的频率依赖因子

在小角度观测条件下,有cos Δθ(tn)≈1,sin Δθ(tn)≈Δθn。经运动补偿后,目标运动模型可近似为转台模型,假设匀速转动的角速度为ω,则有Δθ(tn)=ωtn,此时ΔRp(tn)可近似写为ΔRp(tn)≈yp+xpωtn,式(3)可近似表示为

(4)

将距离频率离散化,令fc+f=f0+mΔf,Δf为频率采样间隔,M为频率采样点数,m=0,1,…,M-1。此时,式(4)可写为

(5)

在成像时间较短且目标尺寸较小时,可忽略越分辨单元徙动(migration through resolution cells, MTRC)的影响,若在成像过程中存在MTRC现象,可利用文献[16]中的方法进行MTRC校正,校正后的目标回波可表示为

(6)

1.2 回波的稀疏表示

利用网格化处理思想,分别令2Δfyp/c=k/K和2f0xpωTr/c=l/L,其中,k=0,1,…,K-1,l=0,1,…,L-1,则ISAR成像场景可离散化为大小为L×K的二维网格,其中距离维有K(K≥M)个网格,方位维有L(L≥N)个网格,此时,式(6)可表示为

(7)

式中:αk l表示网格点(k,l)上散射点的频率依赖因子;σk l表示网格点(k,l)上散射点的散射系数常数复幅度,若网格点(k,l)上存在真实散射点,则σk l不为零,若网格点上不存在真实散射点,则σk l为零。

从式(6)中可以看出,由于频率依赖因子的存在,使得回波信号中的幅度与相位是耦合的。为方便对耦合的二维回波信号进行稀疏表示,将目标回波沿视角方向进行堆叠,则式(7)可矢量化[22,25-27]表示为

(8)

式中：s为矢量化处理后的回波矢量,大小为MN×1维,可写为

s=[S(0,0),…,S(M-1,0),…,S(0,N-1),…,S(M-1,N-1)]T

(9)

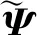
(10)

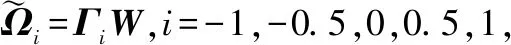
(11)

式中：I表示单位矩阵;⊗表示矩阵的Kronecker乘积;Ti可表示为

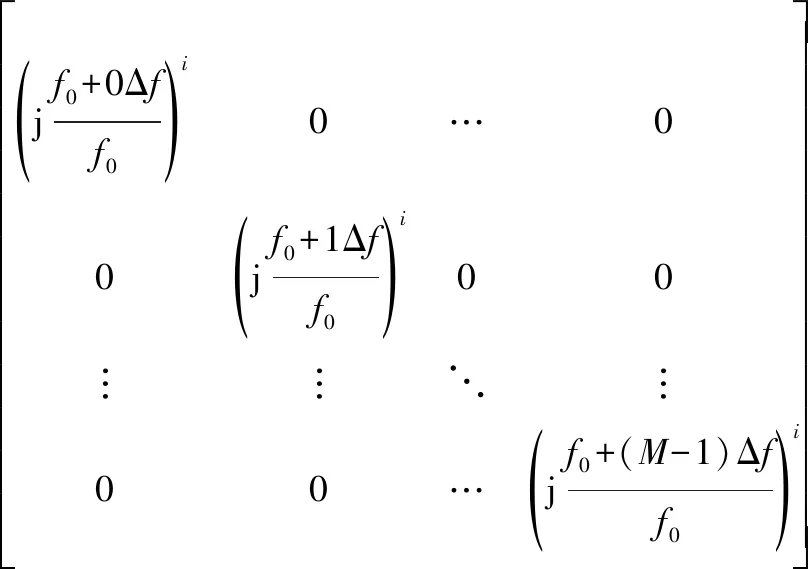
(12)

W为MN×KL维的字典矩阵,可表示为

(13)

其中,

Wn=[Φ(0,0),…,Φ(K-1,0),…,Φ(0,L-1),…,Φ(K-1,L-1)]M×KL

(14)

(15)

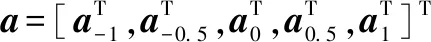
2 多视角多频带ISAR融合成像模型

本文以工作在不同频带且从不同视角观测目标的两部雷达为例进行多视角多频带ISAR融合成像分析。为保证实现融合成像,两部雷达观测目标时获得同一散射中心的信息差距相差不能太大。假设两部雷达相近放置,对目标的观测视角无重合,雷达间的回波信号已经过运动补偿以及互相干等预处理。若在全视角全频带回波中存在因外界干扰或数据传输错误等情况,导致雷达信号中的某一观测频段或观测视角的回波缺失或受到污染,不能用于成像,此时需要利用有效的观测数据实现成像。假设在全视角全频带中有效的观测数据为雷达1和雷达2的回波,通过多视角多频带ISAR融合成像方法可补全缺失的回波数据,与单部雷达相比,可等效提高观测视角和发射带宽,从而改善成像的二维分辨率。

假设Δf为频率采样间隔,雷达1和雷达2的发射信号频带分别为f=f0,f1,…,fM1-1和f=fM-M2,fM-M2+1,…,fM-1,分别包含M1个和M2个频率采样点。全频带可表示为f=f0,f1,…,fM-1,共包含M个频率采样点,则全频带的频率采样数据可表示为f=f0+mΔf(m=0,1,…,M-1)。假设Δθ为角度采样间隔,雷达1和雷达2的观测角度分别为θ=θ0,θ1,…,θN1-1和θ=θN-N2,θN-N2+1,…,θN-1,分别对应N1个和N2个角度。全视角可表示为θ=θ0,θ1,…,θN-1,共有N个角度,全视角的角度采样数据可表示为θ=θ0+nΔθ(n=0,1,…,N-1)。

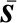
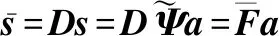
(16)

(17)

(18)

式中:I和0分别表示单位矩阵和零矩阵。

图1 基于矢量化处理的多视角多频带双雷达观测数据融合示意图Fig.1 Multi-angle and multi-band dual radar observation data fusion based on vectorization processing

3 基于OMP算法的融合成像方法

从式(16)可以看出,矢量化后的融合成像模型涉及到大规模的数据重构,因此需要寻找快速有效、简单稳定的稀疏重构算法实现多视角多频带ISAR融合成像。OMP算法[28]原理简单,易于实现,且运算复杂度较低,是一种常用的稀疏重构算法,故本文采用OMP算法求解式(16)。OMP算法的主要实现流程如图2所示。

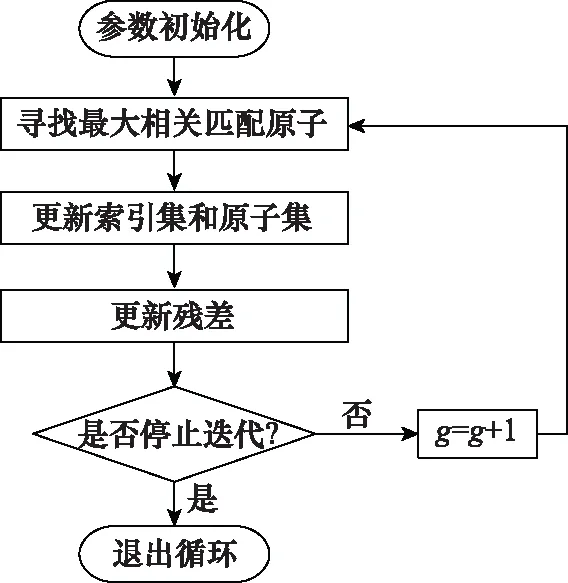
图2 OMP算法实现流程Fig.2 Implementation process of OMP algorithm

OMP算法具体的实现步骤如下:

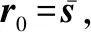
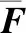
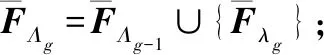
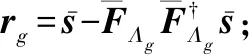
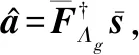
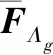
在迭代过程中,OMP算法利用了正交化思想,避免了重复选择原子。对于终止迭代条件,若信号稀疏度已知,则当迭代次数为稀疏度大小时终止迭代,若稀疏度未知,则当残差小于预设门限值时终止迭代。

基于OMP算法的多视角多频带ISAR融合成像方法实现流程如图3所示,主要步骤如下:

步骤 1基于GTD模型得到各雷达回波,进行运动补偿及互相干等预处理,得到相干的距离频域-方位慢时间域回波信号;

步骤 2构造字典矩阵,将回波信号离散化;

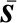
图3 多视角多频带ISAR融合成像流程Fig.3 Multi-angle and multi-band ISAR fusion imaging process

4 仿真与实验分析

本文仿真实验环境为Windows 10 64位操作系统,Matlab 2016A软件平台,仿真所用计算机主要参数如下:处理器为Intel酷睿i5-8265U,主频为1.60 GHz和1.80 GHz,内存为16 GB。本节分别利用简单散射点模型和复杂飞机模型的融合成像仿真实验验证所提融合成像算法的有效性。

4.1 简单散射点模型融合成像

本仿真实验利用简单散射点模型为成像目标进行多视角多频带ISAR融合成像,目标中包含6个散射点,仿真模型如图4(a)所示,其中散射点A和B的坐标分别为(-0.1,-0.1)和(0.1,0.1),对应的频率依赖因子分别为0.5和-1,其余散射点对应的频率依赖因子均为0。雷达工作频带为17～18.5 GHz,采样频率为1.92 GHz,发射脉冲宽度为6 μs,PRF为50 Hz,共发射90个脉冲。在成像时间内,假设目标以0.04 rad/s的角速度匀速转动,累积转角为4.08°,此时雷达的距离分辨率和方位分辨率理论值分别为0.10 m和0.12 m。每个脉冲回波内采样75个距离采样单元的回波数据,经运动补偿后作为全视角全频带回波数据,大小为75×90。利用距离-多普勒(range-Doppler, RD)算法得到的全视角全频带ISAR成像结果如图4(b)所示,由于分辨率足够,从成像结果中可以完全区分所有散射点。

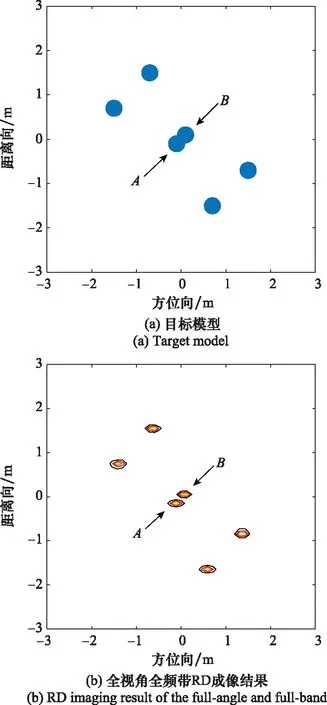
图4 目标模型及其全视角全频带RD成像结果Fig.4 Target model and the RD imaging result of the full-angle and full-band echo data

在全视角全频带回波中取左上角大小为M1×N1的数据作为雷达1的观测数据,取右下角大小为M2×N2的数据作为雷达2的观测数据。令M1=M2=20,N1=N2=25,此时雷达1和雷达2的带宽均为400 MHz,对应的距离分辨率理论值均为0.375 m;雷达1和雷达2的观测角度均为1.13°,但由于各自的中心频率分别为17.2 GHz和18.3 GHz,故两部雷达的方位分辨率理论值分别为0.44 m和0.41 m。当信噪比(signal-to-noise ratio, SNR)为20 dB时,雷达1和雷达2的RD算法成像结果分别如图5(a)和图5(b)所示。从图5可以看出,由于发射带宽和观测视角有限,单部雷达成像的二维分辨率低,导致无法完全区分所有的散射点,影响了成像质量。

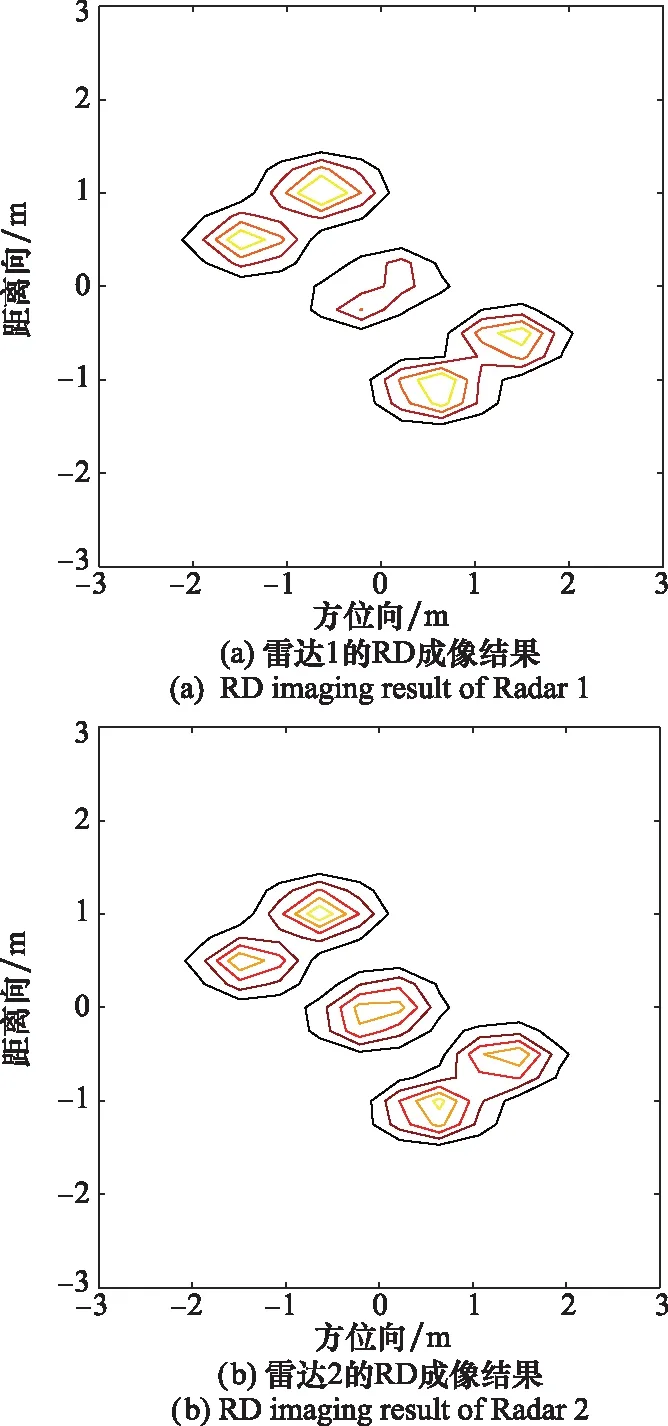
图5 两部雷达的RD成像结果Fig.5 RD imaging results of two radars

直接采用RD算法对两部雷达的观测数据进行融合成像,融合后的距离分辨率和方位分辨率理论值分别为0.187 5 m和0.217 m,成像结果如图6(a)所示。由于频带和视角缺失,RD算法在利用快速傅里叶变换进行二维压缩成像时引起了强烈的副瓣和大量的能量泄露等问题,严重影响了成像质量,无法有效地实现融合成像。分别采用正则化算法[22]和OMP算法实现多视角多频带融合成像,融合后的距离分辨率和方位分辨率理论值分别为0.10 m和0.12 m,与全视角全频带回波的理论分辨率一致,得到的融合成像结果分别如图6(b)和图6(c)所示。从图6(b)可以看出,采用正则化算法可以有效地实现融合成像,与单部雷达成像结果相比改善了二维分辨率,但从融合成像结果中无法完全区分散射点A和散射点B。这是因为正则化算法中需要设置正则化参数,若参数设置不合适则会影响算法的重构性能。从图6(c)可以看出,采用OMP算法能够得到干净清晰的融合成像结果,正确估计出各个散射点的大小和位置,且从成像结果中能够完全区分所有散射点。另外,采用正则化算法和OMP算法实现稀疏重构时所耗的时间分别为1 213.43 s和4.65 s。由于正则化算法在迭代过程中涉及构造大规模矩阵并求逆问题,所需的内存较大且运算时间较长,而OMP算法易于实现且运算过程简单,更适合求解大规模矢量问题。

图6 不同算法的融合成像结果Fig.6 Fusion imaging results of different algorithms

为进一步体现算法对不同频率依赖因子的散射点的重构效果,重点关注散射点A和散射点B的参数估计结果,如表2所示。从表2中的参数估计结果可以看出,利用两种算法均能成功估计出目标散射点的频率依赖因子,其中OMP算法对散射点位置坐标的估计精度比正则化算法更高。

表2 目标散射点参数估计结果

4.2 复杂飞机模型融合成像

为进一步验证算法在复杂目标模型条件下的融合成像性能,利用波音727飞机的回波数据实现多视角多频带ISAR融合成像。飞机的回波数据由美国海军实验室在其网站上提供[29],雷达的载频为9 GHz,带宽为512 MHz,PRF为20 kHz,每个脉冲内截取的距离单元为64个,共发射256个连续脉冲,但考虑到目标的机动性,只利用其中100个脉冲的回波数据作为全视角全频带回波,大小为64×100。全视角全频带雷达的二维回波及其RD成像结果分别如图7(a)和图7(b)所示,从其RD成像结果中可以看出飞机的基本轮廓。

图7 全视角全频带二维回波及其RD成像结果Fig.7 Full-angle and full-band two-dimensional echo data and RD imaging result

4.2.1 不同观测情形下算法融合成像性能验证

为比较在不同观测数据条件下的融合成像效果,在SNR为20 dB条件下,改变雷达1和雷达2的回波数据大小,分别采用正则化算法和OMP算法实现融合成像。

情形 1令M1=M2=25,N1=N2=40。雷达1和雷达2的观测二维回波如图8(a)所示,采用正则化算法和OMP算法得到的融合成像结果分别如图8(b)和图8(c)所示。从图8(b)可以看出,采用正则化法进行融合成像时,虽然可以估计出基本的强散射点,但存在弱散射点丢失的情况,导致丢失了目标结构的一些细节信息,影响了目标的基本形状。从图8(c)可以看出,采用OMP算法进行融合成像时,可从成像结果中分辨出目标形状及其部分细节结构信息,成像效果较好。

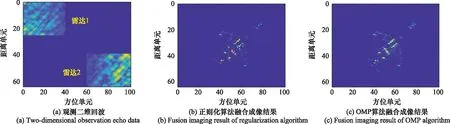
图8 M1=M2=25,N1=N2=40时的观测二维回波数据及融合成像结果Fig.8 Two-dimensional observation echo data and fusion imaging results with M1=M2=25 and N1=N2=40

情形 2令M1=M2=20,N1=N2=30。雷达1和雷达2的观测二维回波如图9(a)所示,采用正则化算法和OMP算法得到的融合成像结果分别如图9(b)和图9(c)所示。从图9(b)可以看出,随着有效观测回波数据的减少,采用正则化算法进行融合成像时容易丢失散射点,特别是机翼和机尾部分散射点丢失较多,导致从成像结果中分辨出目标的基本轮廓比较困难。从图9(c)可以看出,随着观测回波数据的减少,采用OMP算进行融合成像时,仍能得到较为清晰且完整的目标图像。

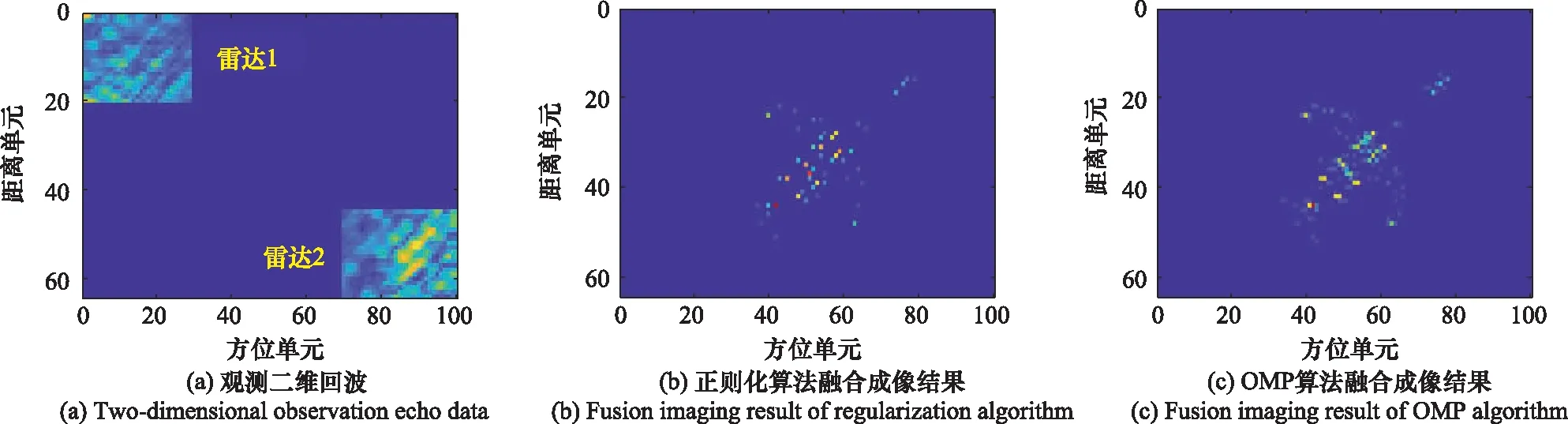
图9 M1=M2=20,N1=N2=30时的观测二维回波数据及融合成像结果Fig.9 Two-dimensional observation echo data and fusion imaging results with M1=M2=20 and N1=N2=30

情形 3令M1=M2=16,N1=N2=25。雷达1和雷达2的观测二维回波如图10(a)所示,采用正则化算法和OMP算法得到的融合成像结果分别如图10(b)和图10(c)所示。从图10(b)可以看出,随着有效观测回波数据的进一步减少,采用正则化算法进行融合成像时,成像结果中不仅容易丢失散射点,还容易引入虚假散射点,导致难以分辨目标的基本轮廓。从图10(c)可以看出,在观测回波数据较少的情况下,采用OMP算法实现融合成像时,虽然在融合成像结果中丢失了少量的散射点,但仍能分辨出目标的基本形状。

图10 M1=M2=16,N1=N2=25时的观测二维回波数据及融合成像结果Fig.10 Two-dimensional observation echo data and fusion imaging results with M1=M2=16 and N1=N2=25

为进一步对比不同有效观测回波数据条件下算法的融合成像性能,采用算法运行时间,图像对比度(image contrast, IC)和目标背景比(target-to-background ratio, TBR)作为算法性能指标[30]。其中,IC可以评价目标图像的整体聚焦质量,值越大表示图像越聚焦,质量越好;TBR能有效表征目标图像的能量聚焦程度,可以评价目标图像的噪声抑制能力和聚焦能力,值越大越好。不同情形下的算法性能衡量指标如表3所示。

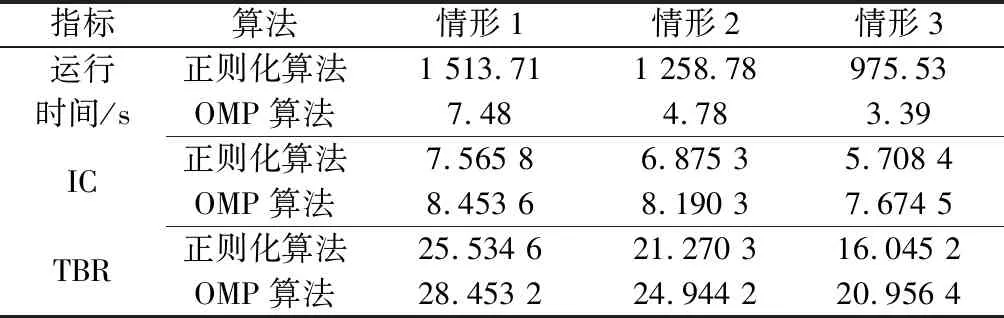
表3 不同情形下的算法性能指标对比

从表3可以看出,在相同的观测回波数据条件下,利用OMP算法得到的成像结果的IC值和TBR值均比正则化算法大,这是因为正则化算法中涉及到正则化参数的估计和调整,若参数设置不合适则会影响算法性能,而OMP算法无需设置参数,可得到较好的融合成像质量。另外,在同一观测条件下,OMP算法的运行时间明显比正则化算法小,这是因为正则化算法中涉及到大规模的矩阵求逆运算,导致运算复杂度较高,运行时间长,不适合大规模数据重构。而OMP算法原理简单且易于实现,拥有快速重构能力,可用于大规模数据稀疏重构,比正则化算法更适用于多视角多频带ISAR融合成像。

4.2.2 不同SNR条件下算法融合成像性能验证

为比较在不同SNR条件下的融合成像效果,令M1=M2=20,N1=N2=30,改变回波数据的SNR,在SNR为20 dB、10 dB和0 dB条件下分别采用正则化算法和OMP算法实现融合成像,成像结果分别如图11和图12所示。从图11可以看出,随着SNR减小,利用正则化算法得到的融合成像结果中目标的轮廓越来越不清晰,特别是当SNR为0 dB时,融合成像结果中存在大量的噪点没有被抑制,严重影响了成像质量,导致无法辨别目标形状结构。这是因为正则化算法的重构性能与噪声水平大小密切相关,在重构过程中需要估计噪声水平参数,若参数估计不准确将会直接影响融合成像质量。从图12中可以看出,随着SNR减小,利用OMP算法均能得到较好的融合成像结果,即使在SNR为0 dB的条件下,仍能从成像结果中分辨出目标的基本形状。实验结果说明与正则化算法相比,OMP算法在低SNR条件下具有更强的鲁棒性。

图11 不同SNR条件下正则化算法的融合成像结果Fig.11 Fusion imaging results of regularization algorithm under different SNRs

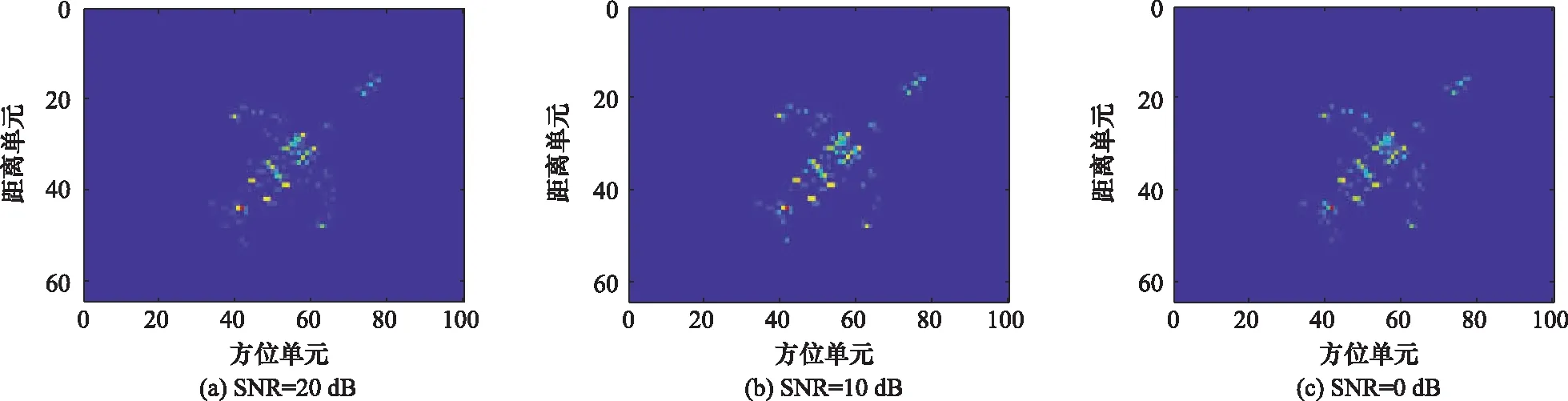
图12 不同SNR条件下OMP算法的融合成像结果Fig.12 Fusion imaging results of OMP algorithm under different SNRs

不同SNR条件下算法性能衡量指标如表4所示。从表4中可以看出,两种算法成像结果的IC值和TBR值均随着SNR减小而减小。在相同的SNR条件下,利用OMP算法所得图像的IC值和TBR值均比正则化算法大,说明在低SNR条件下,利用OMP算法能得到更高质量的图像,体现了本文所提算法的优越性。

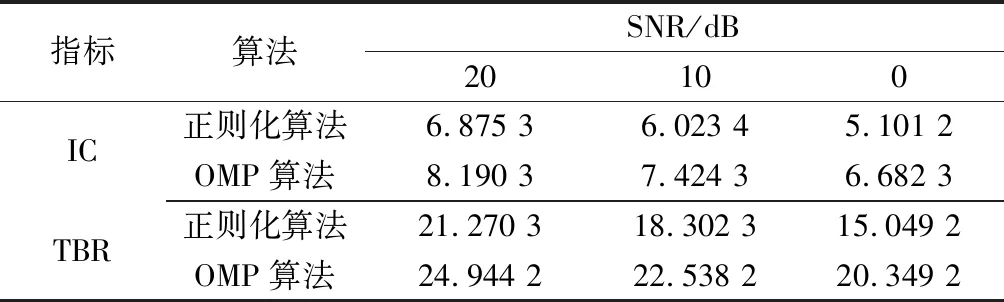
表4 不同SNR条件下的算法性能指标对比

5 结 论

为提高ISAR成像二维分辨率,提出一种基于GTD模型的多视角多频带ISAR融合成像方法。此方法基于GTD模型构建了更符合实际的目标回波,利用稀疏表示理论建立了多视角多频带ISAR融合成像模型,为在保证重构质量的同时提高成像效率,采用OMP算法进行稀疏重构,实现融合成像。仿真实验利用不同目标模型验证了所提算法的有效性,并通过在不同的有效观测数据和不同SNR条件下算法的融合成像性能对比,体现了所提算法在提高成像效率和抗噪性能等方面的优越性。