不等重复试验的多因素方差分析

李沅遥，李晨曦，李 雯

(宜宾学院 理学部，四川 宜宾 644007)

生产活动和科学试验中，结果的产生往往受多个因素影响，不同因素对结果的影响存在差异。方差分析[1-2]是根据试验数据推断一个或多个因素在其水平发生变化时是否对试验结果产生显著影响的一种数理统计方法。

教材[1-2]给出了单因素方差分析和有无交互作用的双因素方差分析的基本理论。戴金辉[3]等将有无交互作用的双因素方差分析进行比较，完善了双因素方差分析理论。陈崇双[4]等对单因素与双因素方差分析进行了线性回归模型重构，证明了方差分析的显著性F检验与回归方程的显著性检验等价。但在实际的生产活动中，影响因素往往是3个及以上，针对这类问题，刘晓华[5]给出了重复试验次数相等时的多元方差分析模型，但由于试验材料昂贵等因素，不等重复试验经常出现。基于王石青[6]和俞纯权[7]的不等重复试验的双因素方差分析，以三因素方差分析为例，进行严格的数学推导，并用乙醇偶合制备C4烯烃的实例加以说明。

1 不等重复试验的三因素方差分析

为减少损失，在正式生产前会对影响结果的因子进行试验。由于客观因素(时间、成本昂贵等)不等重复试验经常出现。以不等重复试验的双因素方差分析为理论依据，将影响因素拓展到3个，建立了不等重复试验三因素方差分析的数学模型。

1.1 模型建立

假定某项试验受3个因素的影响，分别为A、B、C。因素A有l个水平，记为A1、A2、…、Al，因素B有m个水平，记为B1、B2、…、Bm，因素C有r个水平，记为C1、C2、…、Cr。在(Ai,Bj,Ct)组合下进行了nijt次试验，Xijtk表示在组合(Ai,Bj,Ct)下进行第k次试验所得的观测值，每个样本相互独立且服从正态分布Xijtk～(μijt,σ2)。

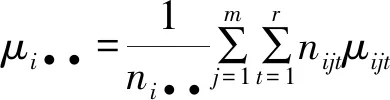
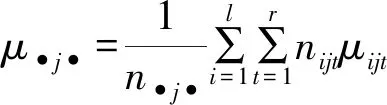
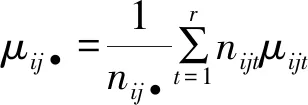
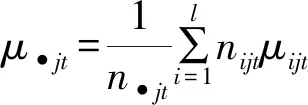
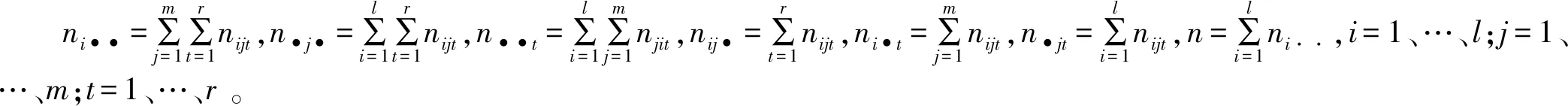
各因子的主效应及交互效应定义为：

αi=μi••-μ为因子A的主效应；

βj=μ•j•-μ为因子B的主效应；

γt=μ••t-μ为因子C的主效应；

ηij=μij•-αi-βj-μ为因子A和因子B的交互效应；

ηit=μi•t-αi-γt-μ为因子A和因子C的交互效应；

ηjt=μ•jt-βj-γt-μ为因子B和因子C的交互效应；

ηijt=μijt-(μij•-μi••)-(μ•jt-μ•j•)-(μi•t-μ••t)-μ为因子A、B和C的交互效应。

不等重复试验的三因素数学模型为：

(1)

在此模型下进行研究分析，任意因子、两因子的交互作用、三因子的交互作用对试验结果的影响是否显著，只需判断因子水平的改变对试验结果是否造成明显改变。现检验因子的各水平效应及因子间的交互效应是否相等，作出以下7个假设检验：

H0A：αi=0，i=1、2、…、l

H0B：βj=0,j=1、2、…、m

H0C：γt=0,t=1、2…、r

H0AB：对任意i、j，均有ηij=0

H0AC：对任意i、t,均有ηij=0

H0BC：对任意j、t,均有ηjt=0

H0ABC：对任意i、j、t,均有ηijt=0

1.2 模型分析

为研究不等重复试验的三因素方差分析，引入以下符号：

由(1)可得以下式子：

(2)

基于不等试验次数的双因素方差分析中平方和的分解思想，不等重复试验的三因素方差分析的总偏差平方和可分解为：

(3)

偏差平方和分解为：

(4)

SE、SA、SB、SC、SAB、SAC、SBC、SABC分别为误差、因素A、因素B、因素C、AB交互作用、AC交互作用、BC交互作用、ABC交互作用的偏差平方和，且满足：

ST=SE+SA+SB+SC+SAB+SAC+SBC+SABC，

其中自由度为：

fT=n-1，fA=l-1，fB=m-1，fC=r-1；

fAB=(l-1)(m-1)，fAC=(l-1)(r-1)，

fBC=(m-1)(r-1)；

fABC=(l-1)(m-1)(r-1)，fE=n-lmr。

以上自由度满足：

fT=fE+fA+fB+fC+fAB+fAC+fBC+fABC。

1.3 模型检验

HOA,HOB,HOC,HOAB,HOAC,HOBC,HABC成立时，由(1)、(2)、(4)可将(3)转化为：

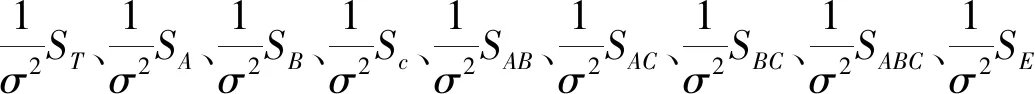
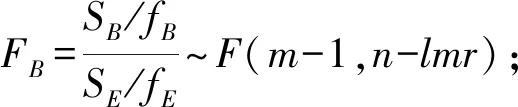
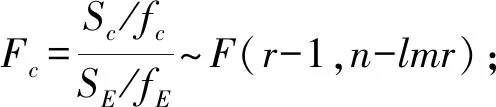
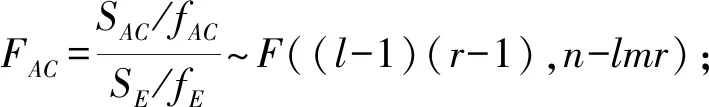
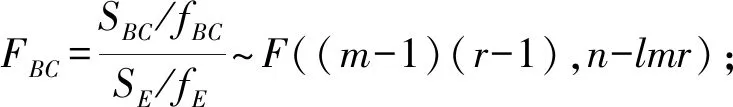
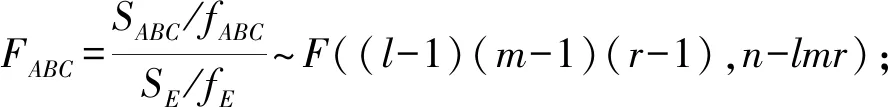
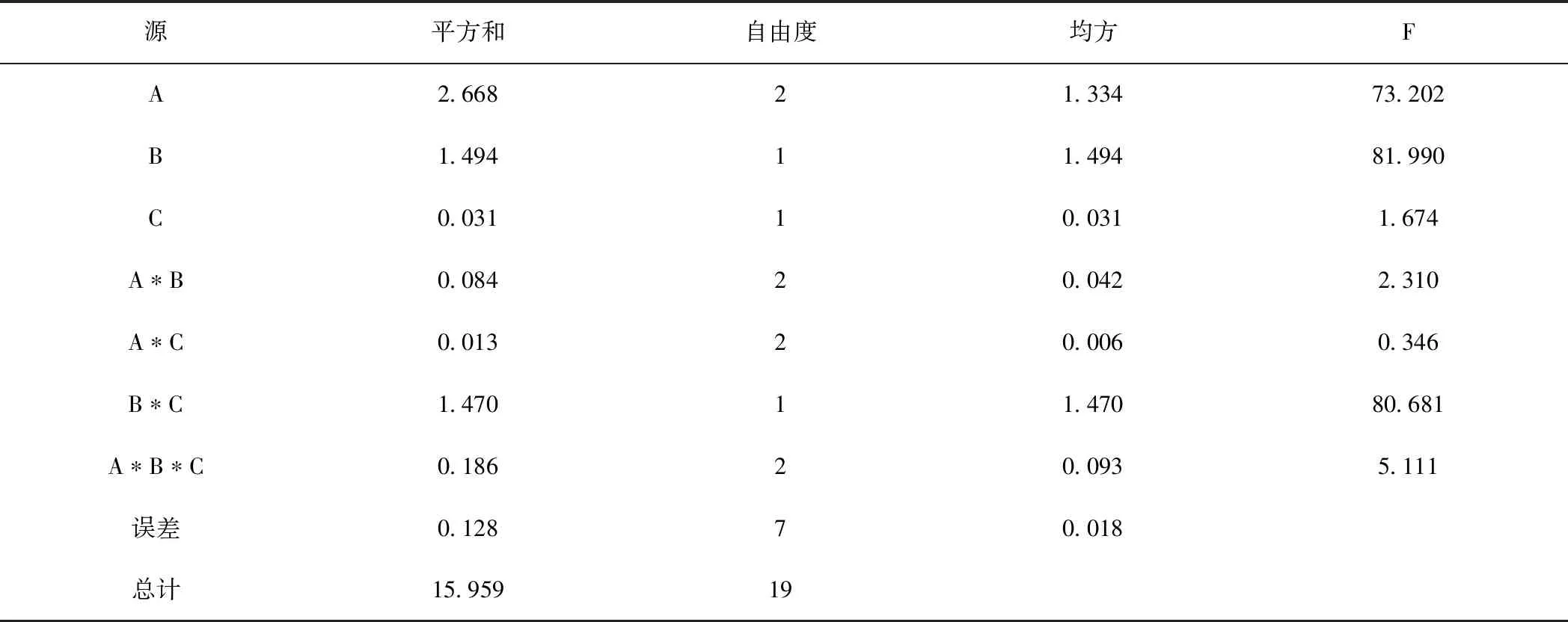
若F>Fα，则拒绝原假设。在不同水平下，随机变量间有差异，认为该因素或因素的交互作用对结果的影响是显著的。若F

2 实例说明

C4烯烃广泛应用于化工产品及医药生产中，而乙醇是生产制备C4烯烃的原料，制备过程中，催化剂组合(即Co负载量、Co/Sio2和HAP装料比、乙醇浓度的组合)与温度会对C4烯烃的选择性、C4烯烃收率及乙醇的转化率产生影响。因此通过对催化剂组合设计，探索乙醇催化偶合制备C4烯烃的工艺条件，具有非常重要的意义和价值，表1为装料比为1∶1时的乙醇转化率。

表1 装料比为1∶1时的乙醇转化率Tab.1 Ethanol conversion at 1∶1 loading ratio

用A表示温度，1代表250℃，2代表300℃，3代表350℃；B表示乙醇的浓度，1代表1.68 mL/min，2代表mL/min；C表示Co负载量，1代表1 wt%，2代表5 wt%。

进行方差分析前，对乙醇的转化率进行正态性、独立性及方差齐性的检验。结果表明，样本不符合正态性及方差齐性，对样本数据进行对数变换，利用spss26进行检验，结果如表2、表3所示。

表2 正态性检验表Tab.2 Normality test list

*.真显著性下限；a.里利氏显著性修正。

表3 方差齐性检验表Tab.3 List of homogeneity test of variance

由表2P>0.05，表明变换后的数据服从正态分布，由表三因素A(温度)、B(乙醇的浓度)、C(Co的负载量)P值均大于0.05，可认为变换后的数据满足方差齐性。

对变换后的样本数据进行方差分析，可见乙醇转化率，结果如表4。

表4 三因素方差分析表Tab.4 Variance analysis of three factors

由表4可知，取定α=0.05时，温度、乙醇浓度、乙醇浓度与Co的负载量的交互作用，温度、乙醇浓度、Co的负载量三者的交互作用对乙醇的转化率有显著的影响，而Co的负负载量、温度与乙醇浓度的交互作用及温度与Co负载量的交互作用对乙醇的转化率影响并不显著。

3 结束语

在不等重复试验双因素方差分析的基础上将影响因素扩展到3个，给出了不等重复试验的三因素方差分析模型，分别从模型建立、平方和分解及统计量构造等方面进行数学推导，通过实例验证了模型的可行性，构建了不等重复试验的多因素方差分析模型。