温度初值问题对配网三芯电缆热评估精度影响分析
深圳供电有限公司 洪锰 华南理工大学电力学院 卢颖
1 配网电缆实时导体温度计算方法
1.1 配网电缆暂态热路模型
结合傅立叶传热定律,配网三芯电缆可以建立暂态热路模型[1-2]。配网三芯电缆结构示意图如图1所示。配网三芯电缆暂态热路模型如图2所示。
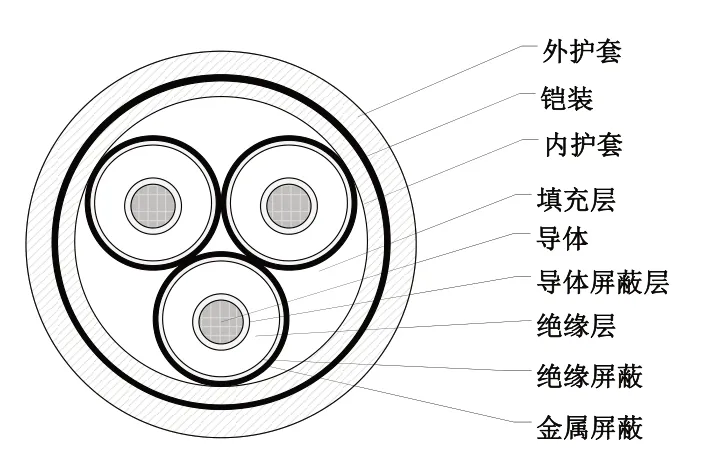
图1 配网三芯电缆结构示意图
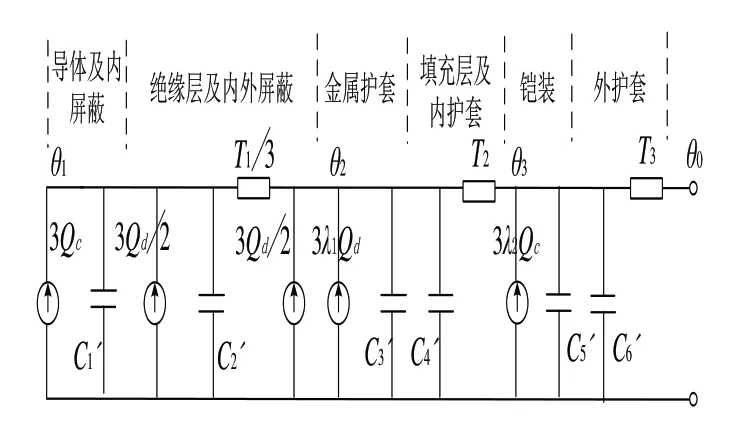
图2 配网三芯电缆暂态热路模型
其中:Qc为单个线芯电缆导体及内屏蔽层产生的损耗;Qd为单个线芯绝缘及绝缘屏蔽层的介质损耗;λ1为单个线芯金属套及屏蔽的损耗因素;λ2为单个线芯铠装层的损耗因素;θ1为电缆导体温度;θ2为绝缘外表面及金属屏蔽层温度;θ3为铠装层温度;θ0为电缆外护套表面温度;T1为单个线芯绝缘层热阻;T2为填充层及内护套热阻;T3为外护套热阻;T4为电缆外部热源至电缆表面介质热阻;C1'为导体及内屏蔽热容;C2'为绝缘层及绝缘屏蔽层热容;C3'为金属套屏蔽层热容;C4'为填充层及内护套热容;C5'为铠装层热容;C6'为外护套热容。
将暂态热路模型中同一节点上的热流源、并联热容合并,可简化为配网三芯电缆简化暂态热路模型,如图3所示。
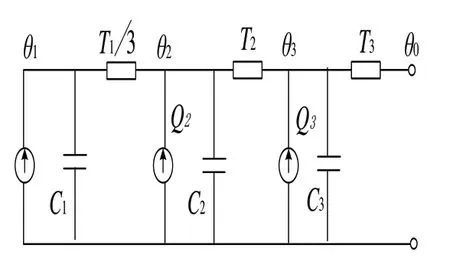
图3 配网三芯电缆简化暂态热路模型
基于热电类比理论,对图3中的配网三芯电缆简化暂态热路模型列写节点方程,通过配网三芯电缆各层结构的等效热参数与电缆温度初值,得出任意时刻的电缆实时导体温度。
配网三芯电缆简化暂态热路模型列写节点方程[3]:
1.2 初值问题描述
基于热电类比理论可以列出电缆暂态热路模型的微分方程组,在给定电缆导体温度的初值作为边界条件的前提下,实现对电缆导体温度的求解。而对于实际运行中的存量电缆线路,由于导体上高压的存在,无法实现对实时导体温度的直接测量。因而计算初值的设置和选取会在电缆暂态热路方程求解时逐步累积产生较大的误差,进而影响导体温度精确计算。电缆负荷往往是连续波动变化,当前时刻的导体温度是电缆历史运行状态累积作用的结果。
2 导体温度初值问题收敛性的证明
2.1 热路模型的简化
对于待解决的导体温度初值问题,新建电缆线路可使用新型内置光纤的电缆直接测量导体温度,但对于存量电缆线路,一般只能通过电缆表皮的温度进行导体温度的推算,针对研究对象即为存量电缆线路。实际中大多数的电力电缆结构复杂,其暂态热路模型对应的微分方程是高阶微分方程,不便于计算。
为了简化计算,在计及电缆各部分损耗的基础上,利用调和平均法,将电缆的各层损耗归算到导体损耗,并将导体外的各层参数归算为同一层,则电缆的暂态热路模型简化为一个只有绝缘层和导体的一阶T 型热容热阻传热模型。此时,电缆热路模型中的微分方程组被简化成为一个一阶热容热阻传热的微分方程:
式中:P1为电缆损耗;CT为简化后的等效热容;TT为简化后的等效热阻;θ1为导体温度;θ2为电缆表皮温度;τ为时间。
为了证明经过一段时间后,导体温度在取任意初值和任意负荷的情况下,仍然能够收敛于一个定值,需要对微分方程进行求解,得出电缆导体温度关于时间的表达式,证明电缆导体温升的过程中,导体计算温度与真实温度的差值随着时间的增大而减小。相较于直接求解电缆暂态模型的微分方程组,求解该一阶微分方程更为简便。
2.2 收敛理论的推导证明
为了求解上述常系数微分方程,得出电缆导体温度关于时间的表达式,需要将有关时间的变量和常数项进行分离。导体的交流电阻Rs是一个与温度有关的函数,直接代入不能对微分方程进行参数的分离和求解,本质上Rs与温度呈线性关系,为了实现参数的分离,将Rs等效为一个只与温度有关的线性函数:
结合电缆热源的计算公式,可得[2]:
对上式的两端分别进行积分,可得:
式中:C为微分方程解中待定参数。
将电缆导体温度的初值作为边界条件带入即可得到其数值:
将式(6)代入式(5)可得:
由式(7)可知,导体温度关于时间的表达式中含有导体温度的初值,因此,需要分析电缆导体温度的初值与指数项的乘积以及导体温度的初值对导体温度收敛性的影响,即分析此时θ1表达式中所含的指数项的值与零的关系。若式(8)成立,则导体温度可收敛。
对式(8)整理可得:
基于传热学理论可以对电缆暂态热路模型中各参数进行计算,进而对电缆导体温度的收敛性进行精确的数学分析。
结合电缆导体交流电阻的计算公式,式(9)可以转变为式(10)[2]。基于式(10)可得满足初值收敛条件下电缆负荷有效值应符合的条件:
为了分析电缆负荷对于收敛速度的影响,需要利用数量级进行估算。对于不同型号的电缆,其电缆结构参数的数量级相差不大,由估算可知TT≈10,α20(1+Ys+Yp)≈104,在20℃条件下电缆导体直流电阻R0≈10-5,将各参数的数量级代入式(11)进行估算,可得I1≈104。对于实际运行中的配网三芯电缆,其正常运行时负荷的有效值最大不超过103的数量级,则可证明式(11)恒成立,即配网三芯电缆导体温度在任意初值的情况下均能收敛于一个定值。
3 收敛速度与导体温度初值的确定方法
取实际配网三芯电缆运行时电流不超过103的数量级进行估算,代入下式(12):
式(12)中:z为电缆负荷和交流电阻对该指数项的影响率,计算结果小于1%,在工程计算中可以忽略。
因此,在工程上,电缆导体温度的表达式可简化为:
为了求解实际导体温度与假定导体温度之间的误差经过多长时间才能收敛到工程上可以接受的范围之内,假设θ1为实际导体温度,θ'1为假定导体温度。定义此时真实温度和假设温度的误差Δθ,则Δθ的表达式为:
由式(14)可知,此时导体实际温度和假定温度之间的误差是以指数进行衰减,即经过一段时间后,导体温度的初值对导体温度的终值的影响逐渐消失。定义工程上实际导体温度和假定导体温度的误差在5%以内可以接受,则:
基于式(15)可以推导得到使导体温度假定值精度满足工程实际需求的收敛时间求解公式:
由式(16)可知,导体温度假定初值和真实初值间的误差越大,收敛时间越长,虽然任意选择导体温度初值最终会收敛于其真实导体温度,但是选择合适的初值将有利于收敛过程的进行。
选定零时刻导体温度初值的方法包括以下三种。
一是取零度与电缆能够长期工作的最高温度的中间值。
二是根据载流量大小预设,令导体初值温度与电缆满载状态下导体温度之比等于初始负荷电流与载流量之比。
三是选择零时刻电缆负荷的稳态导体计算温度作为初值。
第三种选取方式较为接近零时刻导体的真实温度。
4 结论
对导体动态温度的准确测算是实现配网三芯电缆动态增容的前提。现有研究缺乏温度初值选取对电缆动态热评估结果精度影响方面的分析。针对现有存量配网三芯电缆实时热评估是导体温度初值往往无法直接通过测量获取的问题。
基于传热学原理建立了配网三芯电缆的暂态热路模型,并利用调和平均法将多阶热路模型简化为一阶热路模型。通过对一阶微分方程的求解,以比较数量级的方式从理论方面论证了电缆导体温度初值无论如何选取,在经历了一段时间的迭代计算后,导体温度计算结果均能收敛于真实值,为利用历史监测数据实现导体温度的实时监测提供了坚实的理论支撑。

