基于K-means聚类与粗糙集的个人信用集成分类模型
张 怡,谢晓金
(上海工程技术大学 数理与统计学院,上海 201620)
0 引言
随着个人信贷业务的兴起,个人信用风险的不确定性给金融机构带来了巨大损失。因此,针对个人信用风险进行分类成为当今社会的一项重要任务。个人信用分类是金融风险预测在消费贷款中的一项重要应用,其目的是区分“好”和“坏”客户。
目前,已有不少学者对个人信用风险进行了相应研究。陆健健等[1]通过集成随机森林(RF)、GBDT 算法和XGBoost 三种算法后建立的个人信用评估模型,并依据所得相关多元评价指标对个人信用评估进行对比研究。张东梅等[2]基于主成分分析和单类K 近邻对混合数据进行预处理,并结合Bootstrap 方法找到最佳决策边界,对个人信贷数据具有较好的分类效果。刘占峰等[3]基于模糊粗糙集提出的FRIS 算法在个人信用数据评估中优于传统的线性判别分析、逻辑回归和K 近邻算法。而个人信用数据中离散型和连续型数据并存的问题使得分类性能大幅降低[4]。
针对个人信用数据属性杂糅问题的研究,大多从聚类角度对连续型数据进行离散化。石凯等[4]给出多维高斯分布假设下MCMC 算法,具有高度精确的区分效果。李艳等[5]运用K-means 聚类处理混合数据,根据信息熵定义属性重要性度量,建立了变精度正域的约简方法,但基于欧式距离的传统K-means 聚类忽略了空间要素。谢娟英等[6]基于样本空间分布密度改进传统的K-means 聚类,充分解释了其优化算法的客观性。张立军等[7]基于K-means聚类和粗糙集构建集成型分类模型,但无法规避初始点和聚类个数随机选取的弊端。陈晋音等[8]针对混合数据问题,提出了一种自适应选取的改进聚类算法。钟志峰等[9]提出一种自适应改进的K-means 聚类算法,规避了初始点选取的随机性。郭婧等[10]采用菌群优化算法增强Kmeans 聚类的有效性,得到更好的聚类性能。已有文献大多采用K-means 聚类对连续型数据进行离散化,并与属性约简相结合,如采用聚类的思想,在不降低分类性能的前提下,降低求解约简的时间消耗[11]。
综上,针对个人信用数据属性杂糅的问题,本文旨在提出一种改进的K-means 聚类和粗糙集的个人信用集成分类模型。
1 预备知识
1.1 基本概念
定义1样本空间密度
其中,d(xi,xj)表示数据xi与xj之间的欧式距离。density(xi)越小,说明特定空间内样本密集程度越高;反之则越低[6]。
定义2聚类误差平方和
其中,xi是第j个簇的第i个样本点,Cj表示第j个簇的样本点集合,Nj是第j个簇中样本点的个数,μj是第j类的聚类中心。因此,Jej可以反映簇内数据的密集程度,即Jej值越小说明第j个簇内的聚类效果越好[9]。
1.2 基于粗糙集理论的属性约简
粗糙集理论[5,13]的主要思想是利用已知信息,对未知领域进行近似描述。设目标信息系统S是一个四元组S={U,A,V,f},其中U为论域,V是属性值域,f是映射关系。A是一个非空有限的属性集合,由两个相互独立的子集,即条件属性集C和决策属性集D组成。
针对C中非空子集B的重要度计算公式为:
其中,近似质量函数γC(⋅)用于度量特征子集的贡献度[14]。
2 算法改进
2.1 改进的K-means聚类
本文针对K-means 聚类初始点和k值随机选取的缺陷,结合肘部法则[15]和改进的自适应思想,提出一种基于样本空间密度和自适应的改进K-means 聚类,解决个人信用数据中离散和连续型数据并存的问题。
改进的K-means 聚类步骤具体如下:
输入:数据集X=(x1,x2,...xN)、初始簇中心个数k、簇内聚类评估阈值Jejmin、簇内样本点最小个数Nmin和邻域半径调节系数cR[16],簇中心集C=∅,邻域内的数据集D=∅。
输出:簇中心集C。
(1)根据“肘部法则”划分样本点,划分远离群点集X1,得到优化样本集X2。
(2)根据式(1)计算优化样本集X2中每个样本点xi的密度值density(xi),取最小的density(xi)值所对应的样本点xi,利用式(4)计算该样本的邻域半径R及其M邻域内的数据集D。
(3)将样本点xi加入到初始簇中心内,即C=C∪{xi},并从优化样本集X2中删除数据集D。
(4)若簇中心集中簇的个数与设置的k相等,即len(C)=k,则至步骤5,否则返回步骤2。
(5)计算优化后数据集X2内每个样本点xi到C中每个簇中心Cj的距离,并将其划分到距离最小的相应的簇内。
(6)计算k个簇集中的簇中心,若簇中心没有发生变化,则至步骤7,否则返回步骤5。
(7)根据式(2)计算各簇的聚类误差平方和Jej,并计算各簇内的数据样本个数Nj。
(8)根据下列情形条件更新簇中心个数和簇中心集:情形一:若Nj
若簇中心集不发生变化,则至步骤9,否则返回步骤5。
(9)计算远离群点集X1中的每个样本点到各簇中心的距离。若存在样本点到第k个簇中心的距离小于该簇中样本点到簇中心的最大距离,则将该样本点分配到距离它最近的簇中,并从远离群点集X1中删除该样本点,返回步骤6;否则,则至步骤10。
(10)输出最终的簇中心集C。
本文改进的K-means 聚类流程见图1。图中第一个条件判别逻辑为传统的K-means 聚类迭代准则,在此基础上,设定簇内聚类评估指标阈值Jejmin和簇内最小样本点个数的阈值Nmin以实现自动化更新簇中心点和个数。改进的自适应思想体现在第二个条件判别逻辑,即根据肘部准则再次判别远离群点样本集是否发现变化,以此进行迭代更新,从而降低远离群点样本对聚类结果的噪声影响。
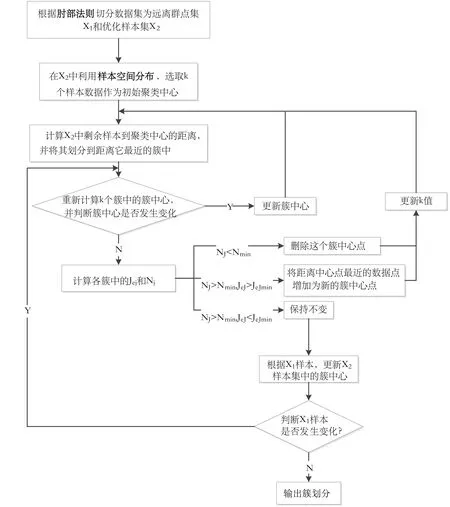
Fig.1 Improved K-means clustering flow图1 改进的K-means聚类流程
2.2 改进的K-means聚类与粗糙集的个人信用分类模型
基于改进的K-mean 聚类和粗糙集的个人信用集成分类模型主要步骤如下:
(1)获取数据集,并将数据进行预处理。首先,计算缺失比,小于5%者,予以删除;反之,使用均值插补法予以填补;其次,进行标准化处理;最后,按照7:3 划分训练集和测试集。
(2)基于2.1 节改进K-means 聚类对训练样本中的连续型数据进行离散化处理。
(3)运用粗糙集对离散化后的训练集进行属性约简,得到特征子集。
(4)为解决不平衡问题,将特征子集加入到基于代价敏感[12]的集成分类模型(以决策树、支持向量机、逻辑回归和神经网络为基模型)中,以Bagging[17]思想进行集成,最终分类结果由动态加权投票法[18]决定。即:
其中,βi表示第i个弱分类器的G-means 得分,表示弱分类器的示性函数,即:
3 实验设置与结果分析
3.1 样本选取与数据来源
选取UCI 上常用的个人信用数据集,分别为Australian Data Set 和Credit Approval Data Set。由表1 可知,各数据集均有离散型和连续型数据并存的特点。

Table 1 Data description表1 数据描述
3.2 数据预处理与参数设置
在数据预处理中,首先,计算各自变量的缺失比,小于5%者删除对应样本点,大于5%者使用均值插补法。其次,对数据进行极大-极小标准化处理,即:
最后,按照7:3 划分训练集和测试集。具体参数设置如表2所示。

Table 2 Cluster parameter setting表2 聚类参数设置
其中,kt表示第t次迭代时簇中心个数,N为样本个数。
由图2 可知,根据“肘部准则”可得最佳初始簇个数k的取值为4。
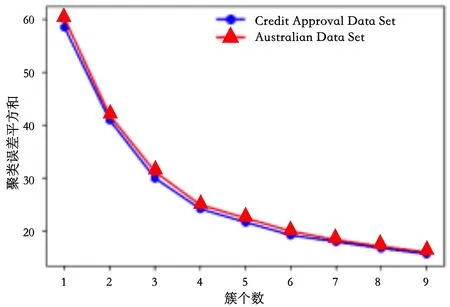
Fig.2 Elbow criteria图2 肘部准则
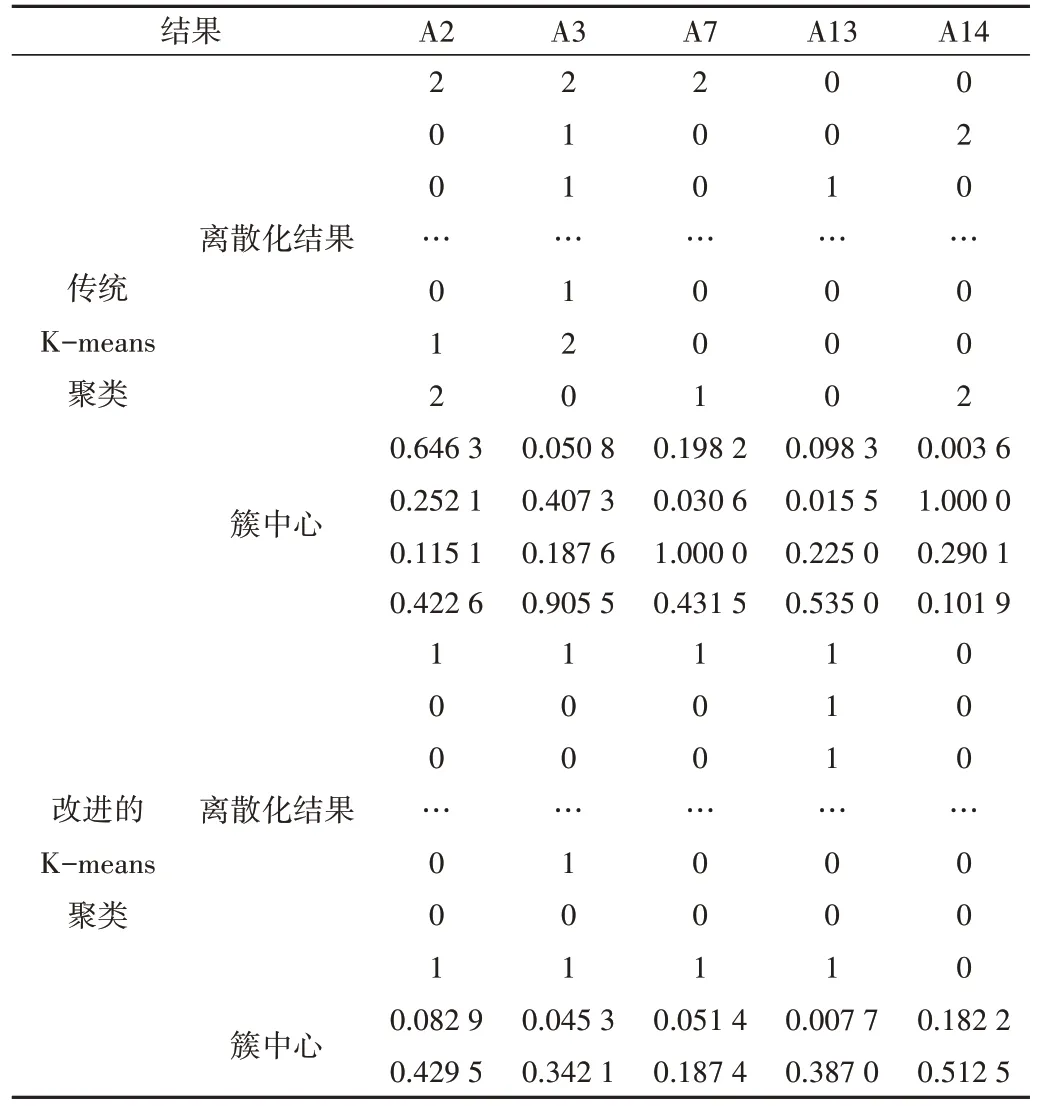
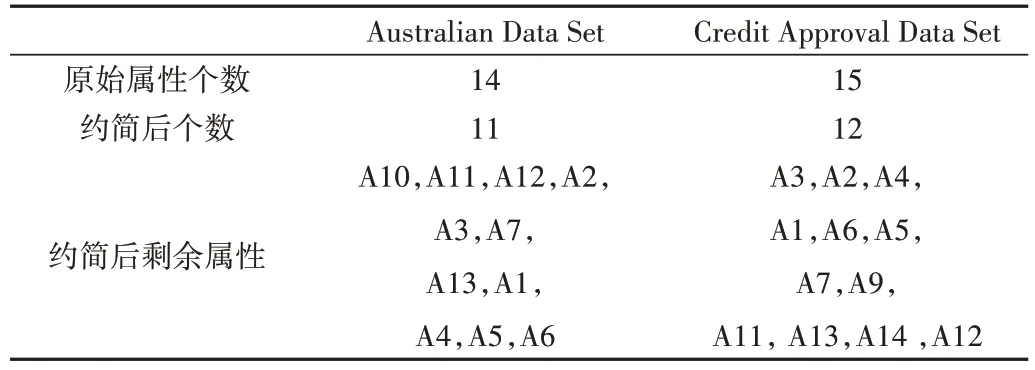
文献[9]指出簇内聚类评估b和簇内样本点最小个数N需根据经验给出固定值,而本文采用自适应参数选取的思想,即b由第t次迭代的样本平均聚类误差乘以适当权重q(1 式(4)中邻域半径cR要尽可能地反映样本的空间分布,过大或过小都无法达到最优的聚类效果[19],故结合肘部准则所得初始簇个数k=4,邻域半径调节系数cR值取0.00005。 针对训练集中的连续型数据,利用改进K-means 聚类方法,可得离散化后的训练集和簇中心,表3 展示了基于Australian Data Set 的离散化结果和簇中心。 Table 3 Australian Data Set’s discretization result and cluster centers表3 Australian Data Set的离散化结果和簇中心 由表3 可知,从聚类离散化结果看,改进的K-means 聚类离散化后的连续型数据更为稀疏,有利于提高后续模型训练和泛化能力;从簇中心结果可见,本文根据改进的自适应思想,将聚类所得簇中心剔除了两个无效簇中心,有效降低了模型的复杂度。 在数据标准化和聚类处理后,基于粗糙集原理,将训练集进行属性约简,约简后的特征子集如表4所示。 在个人信用分类研究中,金融机构更多地关注少数类样本(失信者)的预测准确度。同时,在不平衡数据问题中,对多数类和少数类的整体分类精度进行考虑,是衡量模型优劣的一个重要标志。为此,利用混淆矩阵构造少数类样本召回率rrTP、多数类样本召回率rrTN、G-means[20]和F-value并将其作为评估预测模型性能的指标。其中Gmeans和F-value定义分别为: Table 4 Property reduction result表4 属性约简结果 由式(8)、式(9)可知,G-means综合衡量不平衡数据的分类性能,其值越大说明模型综合分类的预测性越强,可整体反映模型对不平衡数据的分类性能。而F-value则同时考虑了少数类样本的召回率和查准率,其值越大表明模型对于少数类样本的识别能力越强。 本文将文献[5]和文献[9]的方法作为对照组A 和对照组B。对照组A 和对照组B 分别采用传统K-means 聚类和自适应K-means 聚类对连续型数据进行离散化。而本文基于样本空间密度和改进的自适应思想对连续型数据进行离散化处理,再运用粗糙集获得最优特征子集。为比较三者模型性能,基于上述数据预处理、属性约简和模型调参,得实验结果如表5所示。 Table 5 Results of performance evaluation indicators表5 性能评价指标结果(%) 从模型预测性能提升的角度看,针对Australian Data Set,实验组加权得分后的G-means和F-value为79.08%和77.42%,较对照组A 分别提高了4.62%和4.74%,较对照组B 分别提高了5.35%和6.83%;针对Credit Approval Data Set数据集,实验组加权得分后的G-means和F-value为87.82% 和86.67%,较对照组A 分别提高了1.40% 和1.61%,较对照组B 分别提高了0.45%和0.48%。由此,可以直观看出本文模型整体预测效果和精度更好。 针对个人信用数据属性杂糅问题,本文提出一种基于改进的K-means 聚类与粗糙集相结合的个人信用集成分类模型,旨在综合衡量离散型和连续型数据并存时对分类性能的影响,且在不降低分类性能的前提下,删除冗余特征,以最大化提高模型效率,并验证其在个人信用数据集上的有效性。实验结果表明,本文模型较已有模型具有更优的分类性能,分类策略也较以往研究有所补充完善。不足之处是邻域半径调节系数需要根据经验设定。3.3 基于改进K-means聚类的数据离散化
3.4 基于粗糙集的属性约简
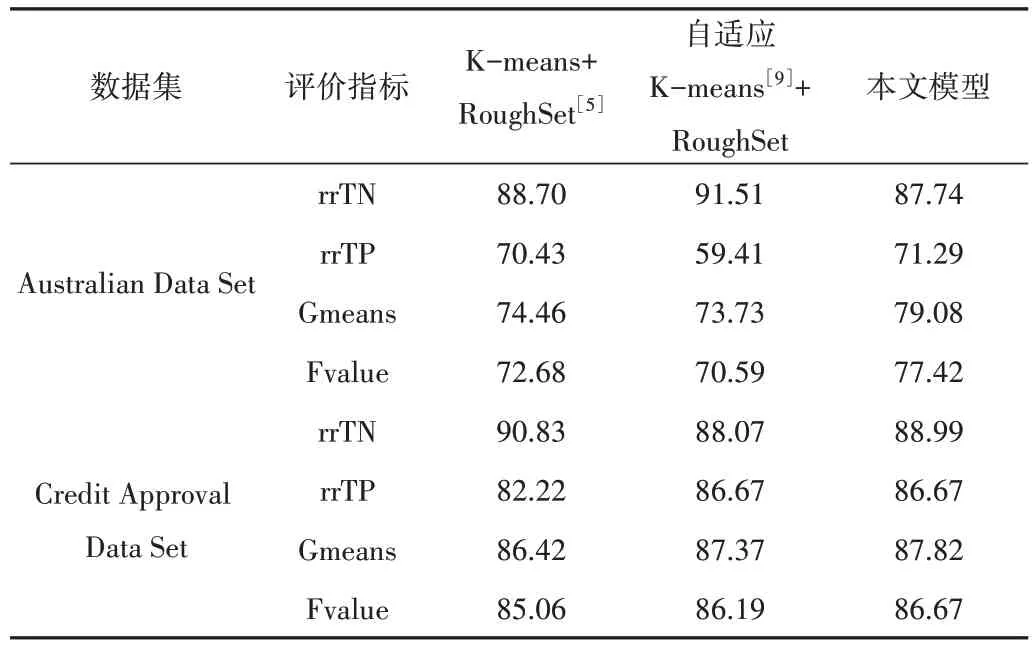
3.5 性能评价指标
3.6 实验结果分析
4 结语

