引入方差/波动率资产的动态最优投资组合
周春阳, 吴冲锋
(上海交通大学安泰经济与管理学院, 上海 200030)
0 引 言
波动率是重要的市场变量,对投资者进行投资决策和风险管理具有重要的参考价值.例如,芝加哥期权交易所基于期权价格构建的波动率指数VIX (volatility index),反映了投资者对未来市场波动的预期(1)计算VIX波动率指数的主要思想是通过一系列标普500指数虚值期权来复制30天期限的方差互换,由无套利定价原理可知,该期权组合的价格等于方差互换的价格,或VIX波动率指数的平方.VIX指数反映了投资者对市场波动的预期,VIX指数越高,投资者为转移波动率风险所需要支付的成本越高.VIX的具体算法可以参阅芝加哥期权交易所波动率指数白皮书(见https://cdn.cboe.com/resources/futures/vixwhite.pdf).,已经成为投资者把握市场情绪和管理投资风险的重要指标.众多研究文献指出,VIX指数对未来市场收益率、波动率和相关性有显著的预测能力[1-3],投资者在构建组合时考虑期权隐含波动率信息能够提高组合的投资绩效[4, 5].
由于波动率变动同股票收益率呈负相关关系,特别是在不利市场条件下两者的相关性更低[5],因而以方差/波动率为标的的方差/波动率资产,能够为投资者提供一个良好的分散股票风险的工具.在美国等发达国家金融市场,从场外柜台市场的方差互换,到交易所市场基于波动率指数派生出来的VIX期货、期权、ETF和ETN等金融产品,交易都非常活跃.在学术研究方面,Dash和Moran[6]、Szado[7, 8]和Yan等[9]的研究表明,在传统的股票债券等资产组合中加入VIX期货或VIX期权等波动率资产有助于分散投资组合(下端)风险,Hilal等[10]基于极值理论研究如何使用VIX期货对冲股票市场的黑天鹅风险.
可见,方差/波动率资产可以从如下两个方面影响投资者的投资决策:一方面,方差/波动率资产的价格反映了投资者对市场波动的预期,是重要的市场状态变量;另一方面,方差/波动率资产同股票收益率呈负相关关系,有助于分散股票组合风险.以往文献往往单独考虑上述两个因素对最优投资组合的影响.本文在传统的股票资产和无风险资产组合中引入方差/波动率资产,在投资者具有幂效用函数的假设下,给出了动态最优投资组合的显示解.本文综合考察方差/波动率资产作为状态变量和风险分散工具对最优投资组合权重和投资组合绩效的影响,并通过经济成本分析,研究方差/波动率资产对投资者期望效用的影响.
研究发现,方差/波动率资产价格是影响投资者投资决策的重要状态变量.随着方差/波动率资产价格的增加,投资者会降低股票资产和方差/波动率资产的投资权重,增加无风险资产的投资权重.本研究同时求解了组合中不包含方差/波动率资产的动态投资组合问题,并考察不包含方差/波动率资产给投资者带来的经济成本.基于美国标准普尔500全收益指数和VIX期货数据的实证结果表明,组合中加入VIX期货有助于分散组合风险.组合中不包含VIX期货会导致投资者在市场风险较小的时候过于谨慎,而在市场风险较高的时候承担了较高的市场不利变动风险,缺乏VIX期货作为风险分散工具导致投资者遭受较高的经济成本.最后,样本外实证结果表明,在传统的股票和无风险资产组合中加入VIX期货有助于提高投资收益和获得更高的夏普比.
1 方差/波动率资产的价格动态过程和动态最优投资组合问题
1.1 模型假设
令St和Xt分别代表t时刻股票资产及对应方差资产的价格,借鉴Chacko和Viceira[11],假定他们服从以下随机微分方程
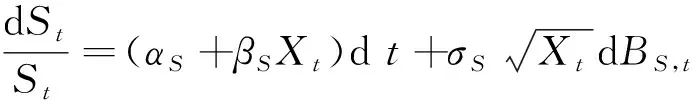
(1)
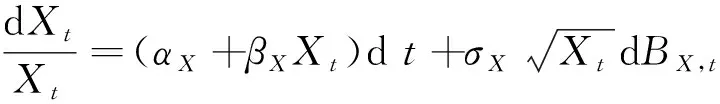
(2)
其中〈dβX,t,dβS,t〉=ρdt,式(1)和式(2)表明,方差风险是影响股票资产和方差资产期望收益的系统性风险,其中βS和βX分别刻画了股票资产和方差资产的风险溢价;同时,两种资产收益率的波动程度也会随着方差资产价格的增加而增加.
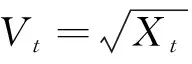

(3)
式(2)和式(3)的模型参数存在以下对应关系

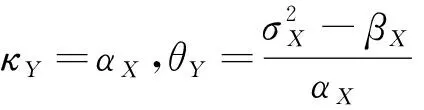
最后,假设投资者具有幂效用函数,即
其中WT代表投资者在期末的财富,γ>0代表投资者的相对风险厌恶系数.
1.2 包含方差/波动率资产的动态最优投资组合
令
其中当M=X时代表方差资产,当M=V时代表波动率资产.由式(1)~式(3),有
投资者可以投资股票资产St,方差或波动率资产Mt,以及无风险资产r.令
代表股票资产和方差/波动率资产的权重构成的向量,则投资者财富的动态过程可以写作
(4)

命题1给定财富动态过程如式(4)所示,不考虑卖空和借贷约束,投资者最大化期末财富效用函数
(5)
式(5)的最优动态投资组合可以写作
(6)
其中ΣZ,At和Bt分别由附录A中式(A2)、式(A8)和式(A9)给出.证明见附录A.

1.3 不包含方差/波动率资产的最优投资组合
当组合中不包含方差/波动率资产时,投资者财富的动态过程可以写作
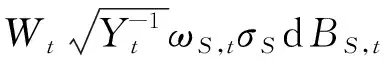
(7)
此时有以下命题成立.
命题2给定财富动态过程如式(7)所示,不考虑卖空和借贷约束,投资者最大化期末财富效用函数式(5)的最优动态投资组合为
(8)
其中AS,t和BS,t分别由附录B中式(A11)和式(A12)给出.证明见附录B.
1.4 组合中不包含方差/波动率资产的经济成本
为了考察在组合中不加入方差/波动率资产给投资者带来的经济成本,类似于Li和Zhou[12],求解以下方程

2 实证研究
2.1 数据和参数估计
本文采用的数据是美国标普500全收益指数和VIX期货连续合约,数据样本区间为2005年1月3日至2018年12月31日共3 651个交易日数据.计算了两种资产的对数收益率并乘上100,其样本统计量如表1所示.可以看到同标普500全收益指数相比,VIX期货具有更大的标准差和峰度,表明VIX期货更有可能发生较大的波动.标普500全收益指数收益率具有负的偏度,而VIX期货具有正的偏度,即股票资产更有可能发生负向变动,而波动率资产更有可能发生向上的正向变动.最后,两种资产的相关系数为-0.654 0.

表1 资产对数收益率的样本统计值Table 1 Summary statistics of logarithmic assets returns
采用Ait-Sahalia和Kimmel[13]的方法对模型(1)和模型(3)进行估计,估计结果如表2所示.βS的估计值较小且不显著,表明波动率的增加不能显著提高股票资产的风险溢价.βV的估计值为-0.001 4,且在1%水平上显著.由模型(3)可知VIX期货价格的长期均衡值为

表2 参数估计结果Table 2 Result of parameters estimates
ρ的估计值为-0.661 0,且在1%水平上显著,即股票收益率和波动率变动之间存在负相关关系.最后,股票资产的波动率σS和VIX期货的波动率σV均显著,但前者要远小于后者.
2.2 最优动态投资组合和经济成本
根据命题1和命题2,求解包含VIX期货和不包含VIX期货时的最优投资组合问题.投资者风险厌恶系数设为10,无风险利率设为0.03,投资期限为1年.图1画出了不同VIX期货价格下投资者的最优投资组合权重.可以看到,不管是否包含VIX期货,风险资产的权重都会随着VIX期货价格的增加而降低,而无风险资产的权重会随着VIX期货价格的增加而增加.
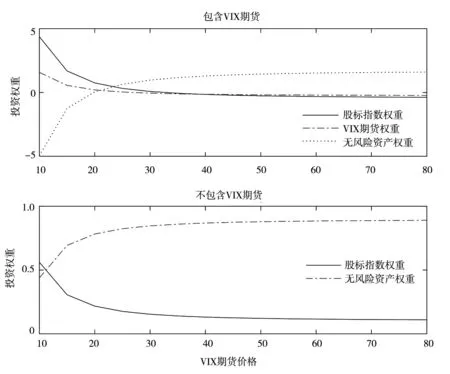
图1 最优动态投资组合Fig.1 Optimal dynamic portfolio allocation
当组合中包含VIX期货时,投资者在VIX期货价格较低的时候会投资较高比重的风险资产.例如,当VIX期货价格为10的时候,此时市场整体的风险较低,股票资产会有较高的吸引力;同时由于VIX期货价格位于均衡值以下,有较大的概率向上回复.因而,投资者在标普500指数和VIX期货的投资权重分别为4.371 2和1.293 8,即风险资产的总权重达5.665,而无风险资产的权重为-4.665.当VIX期货价格增加时,投资者会迅速降低风险资产的比重.当VIX期货价格接近30时,风险资产的权重基本接近于0.当VIX期货价格达到较高水平,投资者此时会同时做空标普500指数和VIX期货.例如,当VIX期货价格为80时,标普500指数和VIX期货的权重分别为-0.378 2和-0.168 5,无风险资产的权重为1.546 7.此时尽管股票资产可能出现反弹而出现亏损,但是VIX期货价格向下均值回复,会有效降低组合的风险.
相比而言,如果组合中不包含VIX期货,投资者在VIX期货价格较低时对风险资产的投资会谨慎很多.例如,当VIX期货价格为10的时候,标普500指数的投资权重仅为0.571 3.当VIX期货价格进一步上升时,投资者会降低对标普500指数的投资.但是当VIX期货价格增长至30以上时, VIX期货价格的变化对风险资产权重的影响非常小.即使在VIX期货价格为80时,投资者在标普500指数的投资权重仍达到0.107 4.此时投资者承担了较高的市场价格波动风险.
根据命题1和命题2,表3将风险资产的投资权重进一步分解为均值方差静态组合权重和跨期对冲需求权重,分别对应于式(6)或式(8)的第1项和第2项.
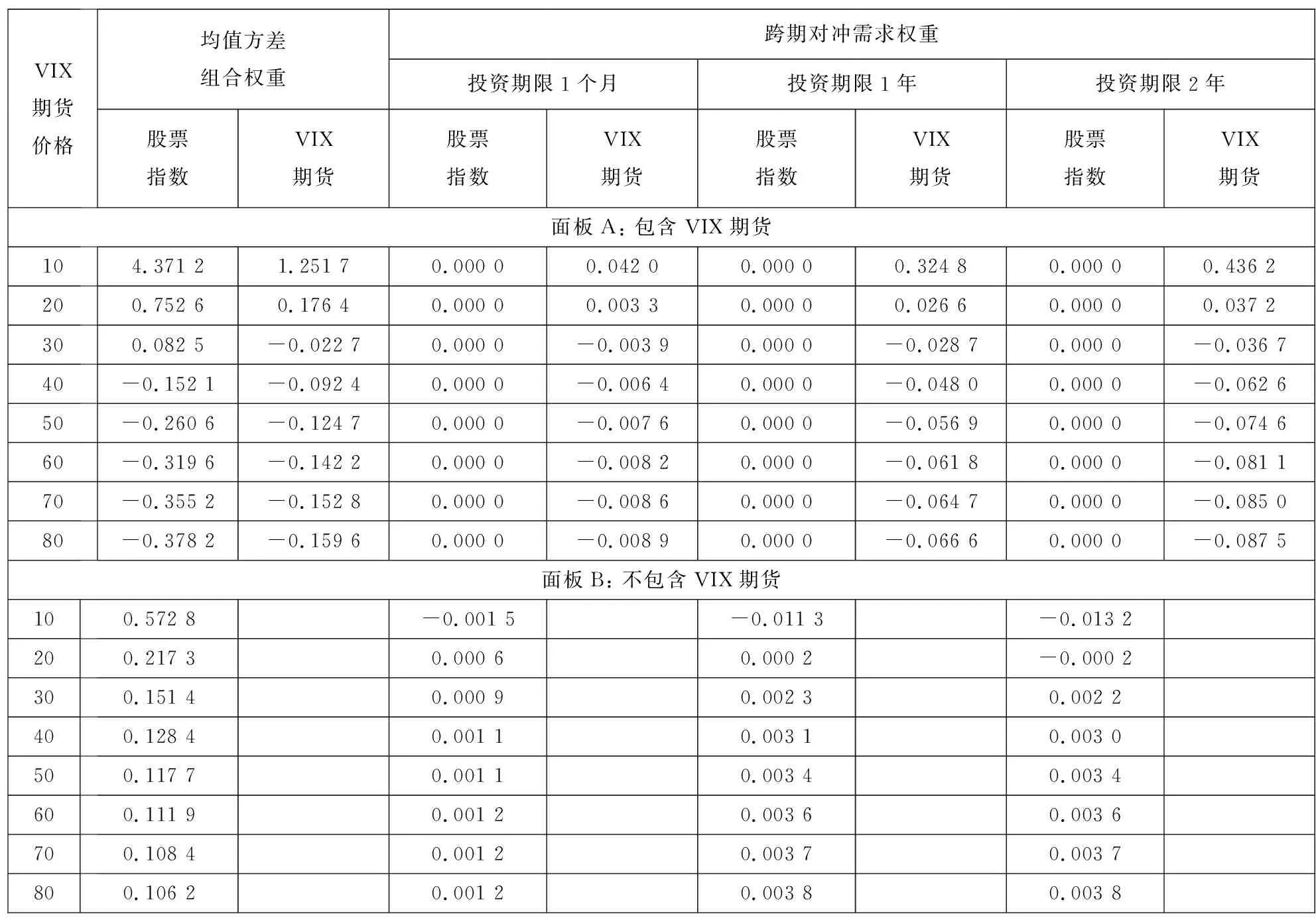
表3 投资组合权重的两个组成成分Table 3 Two components of portfolio weights
由面板A可以看到,当组合中包含VIX期货时,均值方差组合在VIX期货价格较低时同时买入股票和VIX期货,而在VIX期货价格较高时同时卖出股票和VIX期货.由命题1后续的评论可知,股票指数的跨期风险对冲需求为0,而VIX期货的跨期风险对冲需求是VIX期货价格的减函数.表3中的实证结果和本研究的理论结果相一致,也具有直观的经济解释.由于VIX期货价格存在均值回复特性,因而当VIX期货价格较低时VIX期货的跨期对冲需求为正,而当VIX期货价格较高时VIX期货的跨期对冲需求为负.
当组合中不包含VIX期货时,由命题2后续的评论可知,股票指数的均值方差组合权重和跨期对冲需求权重都随着VIX期货价格的增加而降低.面板B中的实证结果与本研究理论结果也是一致的.随着VIX期货价格的增加,风险厌恶的投资者在均值方差组合中会降低股票指数的投资权重,相应增加无风险资产的投资权重.同样,考虑到VIX期货的均值回复特性,投资者在VIX期货价格较低时会担心VIX期货价格回升从而降低股票的投资权重,因而此时股票的跨期对冲需求为负.相应的,当VIX期货价格较高时,投资者的跨期对冲需求为正.
图2给出了当包含VIX期货时,投资者在不同投资期限下的最优组合权重.同表3的结论一致,标普500指数的跨期风险对冲需求为0,因而其权重不会随着投资期限的变化而变化.而VIX期货权重的跨期需求依赖于VIX期货价格水平.可以看到,当VIX期货价格较低时,由于VIX期货价格有向上均值回复的趋势,此时VIX期货有正的跨期风险对冲需求,即VIX期货的投资权重会随着投资期限的增加而增加.而当VIX期货价格较高时,此时VIX期货价格有较大的可能性会向下均值回复,此时VIX期货的投资权重会随着投资期限的延长而降低.

图2 不同投资期限下的最优投资组合Fig.2 Optimal portfolio allocation under different investment horizons
最后,图3给出了组合中不包含VIX期货对投资者带来的经济成本.首先,当VIX期货价格较低时,投资者由于没有在市场风险较低的时候充分投资风险资产,此时会遭受较高的经济成本.可以看到,当投资期限为1年,VIX期货价格为10时,经济成本达0.304 9元,即需要额外支付30.49%的财富给投资者,才能使他愿意在组合中不加入VIX期货.其次,当VIX期货价格较高的时候,投资者由于没有在市场风险较高的时候规避风险,或采用VIX期货来分散和对冲股票市场风险,同样也会遭受较大的经济成本.可以看到,当VIX期货价格为80时,经济成本达到0.182 3元.当VIX期货价格接近其均衡价格时,不包含VIX期货所导致的经济成本相对较小.
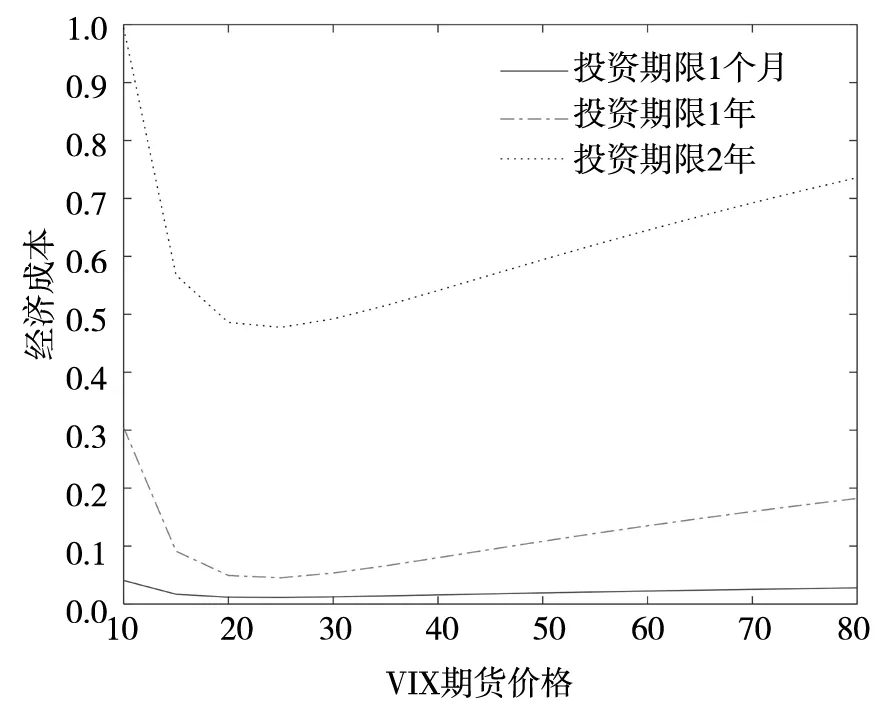
图3 组合中不包含VIX期货的经济成Fig.3 Economic cost of exclusion of VIX future in the portfolio

2.3 样本外投资绩效


表4 组合的样本外投资绩效(T=20 d,γ=10)Table 4 Out-of-sample portfolio performance(T=20 d,γ=10)
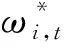
表4中的第1行给出的是股票和无风险资产等权组合的绩效表现.该组合虽然风险较小,但收益率最低,最终在3个模型中夏普比率最低.第3行给出的是不包含VIX期货的动态投资组合的绩效表现.同等权组合相比,该组合能够获得较高的收益率和夏普比率,表明考虑波动率时变风险有助于提高组合绩效[15].最后,第4行给出的是包含VIX期货的最优投资组合的样本外绩效.可以看到,加入VIX期货的动态投资组合具有更高的波动风险,年化波动率是前述两个模型的两倍.图1的结果表明,由于VIX期货和标普500指数存在风险分散的效果,在VIX期货价格很低或很高的时候组合中风险资产权重的绝对值都比较大.考虑到模型不确定性因素的影响,风险资产的高权重可能会导致组合波动率增加;同时,较高的风险资产权重也使得组合的成交额更高.与另外两个模型相比,该模型也获得了更高的收益和更高的夏普比.
为了检验表4中的结果在不同的参数下是否稳健,表5给出了投资期限分别为10天和30天,风险厌恶系数分别为5和20时组合的样本外绩效.同表4的结论一致,表5的实证结果表明,在股票组合中加入VIX期货有助于提高组合收益和收益风险比.同时,同投资期限相比,投资者风险厌恶系数对组合波动率和风险资产成交规模的影响更为显著.特别的,较高的风险厌恶程度有助于降低组合的波动率以及风险资产的成交额.
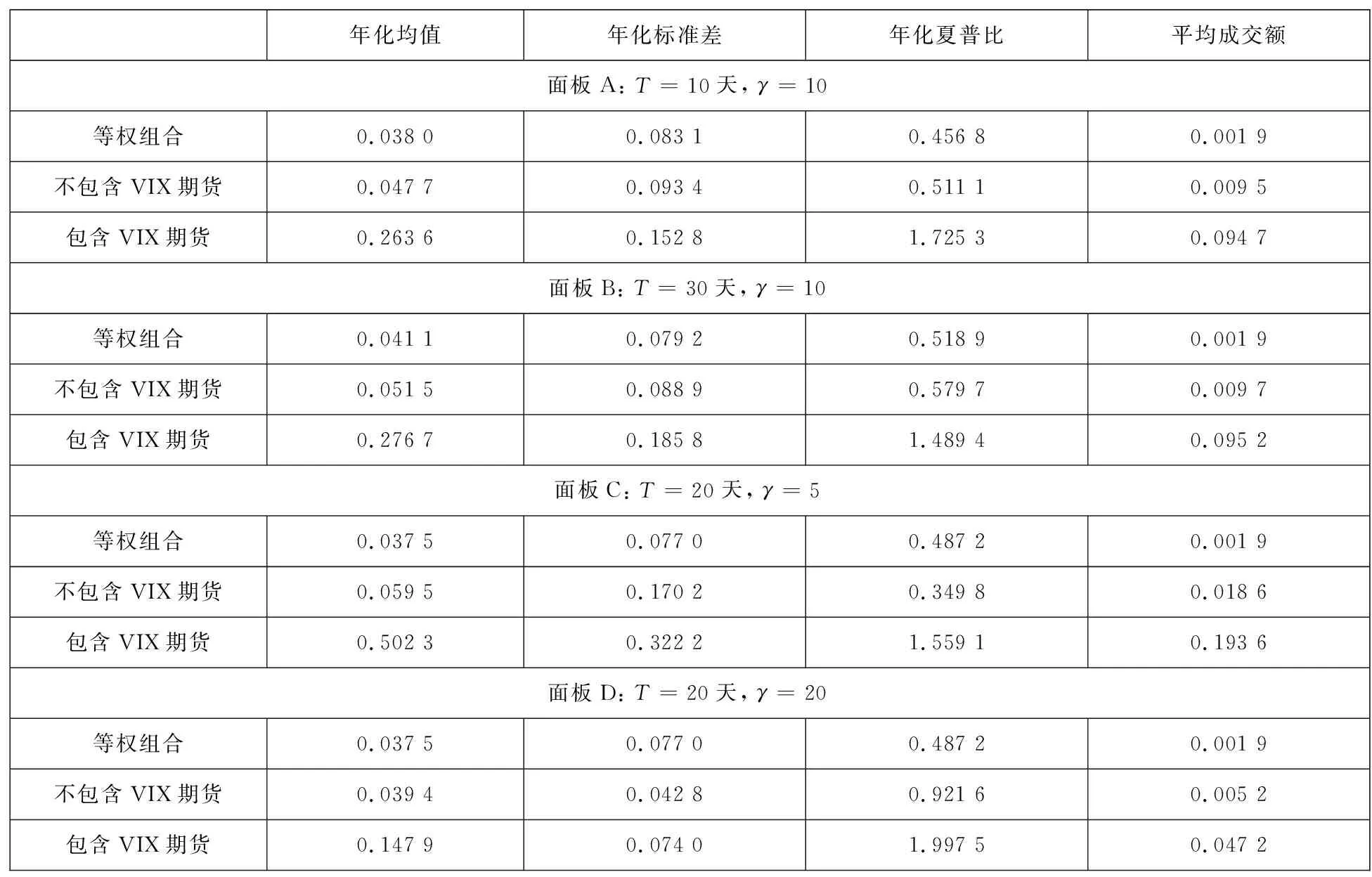
表5 不同参数下各个组合的样本外投资绩效Table 5 Out-of-sample portfolio performance under different investment horizons and risk aversions
3 结束语
方差/波动率是重要的市场状态变量,是投资者进行投资决策的重要指标;同时,方差/波动率资产和股票资产价格变动存在负相关关系,股票组合中引入方差/波动率资产有助于分散组合风险.本文在组合中除了包含传统的股票资产和无风险资产之外,还包含了方差/波动率资产,并给出了动态最优投资组合的显式解.
研究发现,方差/波动率资产价格是影响投资组合权重的重要状态变量,其价格的增加反映了市场波动程度的增加,从而导致股票资产以及方差/波动率资产权重的降低.基于美国标普500全收益指数和VIX期货的实证结果表明,组合中加入VIX期货有助于分散组合风险和提高投资组合样本外绩效.组合中不包含VIX期货会导致投资者在市场风险较小的时候过于谨慎,而在市场风险较高的时候承担了较高的市场不利变动风险,从而导致投资者遭受较高的经济成本.
样本外实证结果表明,在股票组合中加入VIX期货有助于提高组合收益和收益风险比.然而,当投资者具有较低的风险厌恶系数时,VIX期货的加入提高了风险资产的权重和成交规模.在存在模型不确定性的情况下,高风险资产权重容易导致组合的波动率增加;而当交易手续费较高时,较高的成交规模会侵蚀组合的收益.在引入方差/波动率资产构建组合时考虑交易成本的影响,值得进一步深入研究.
附录A
命题1的证明:
令J(W,Y,t)=maxEt(u(WT))代表式(5)的值函数,则满足以下HJB方程
(A1)
其中
(A2)
且J(W,Y,t)的终值条件为
(A3)
借鉴Chacko和Viceira[11]的做法,推测值函数可以写作
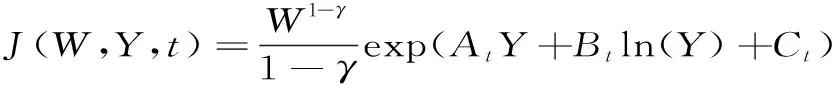
(A4)
其中At,Bt和Ct为时间t的函数,且满足终值条件AT=BT=CT=0.将式(A4)代入式(A1)可以得到
(A5)
上式的一阶条件为
因而最优动态投资组合为
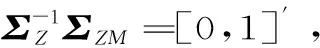
(A6)

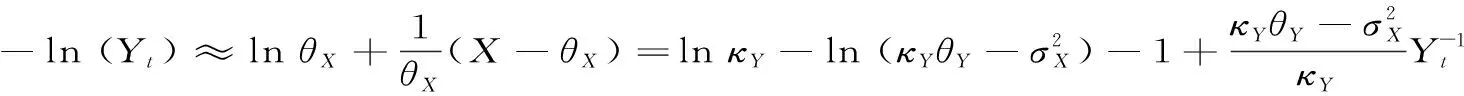
其中
代表方差资产价格的长期均衡值.可以将式(A5)写作
(A7)
其中
以及
为了保证式(A7)对任意的Yt都成立,At应满足以下常微分方程
并且由终端条件AT=0,可以得到At的显示解为
(A8)
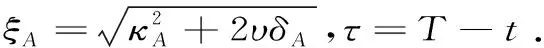
类似的,有Bt满足以下常微分方程
并且由终端条件BT=0,可得方程的解为
(A9)


在实证分析中,采用梯形数值积分方法求解上式.
证毕.
附录B
命题2的证明:
类似于命题1的证明,值函数J(W,Y,t)=maxEt(u(WT))可以写作
且满足以下HJB方程
(A10)
由一阶条件可得最优解为
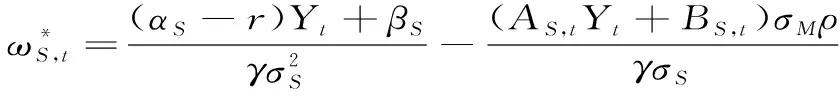
将其代入式(A10), 可求得

(A11)
(A12)
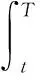
(A13)
其中
且
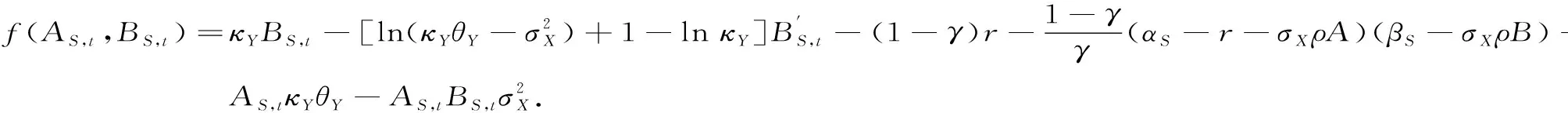
证毕.

