无人机离机轨迹与姿态的高准度快速预测方法研究

孙 博，高永卫，魏斌斌

(1 西北工业大学航空学院，陕西 西安 710072；2 西安交通大学航天航空学院，陕西 西安 710049)

0 引言

无人机可以实现多机协同作战,执行侦察、干扰和网络中继等任务,经济可行性高,具有广阔的军事应用前景[1-2]。由于无人机飞行速度和航时的限制,往往需要大型载机在战区外对无人机实施投送,为战区内无人机协同作战奠定基础。载机对无人机的投送有以下特点：1)载机的动能和势能可以施加于无人机,增加了无人机的初始速度和高度;2)投送过程中,无人机受载机影响强[3-4];3)相较于其他分离物,无人机的气动外形更复杂、升力和力矩特性的影响更显著;4)无人机投送姿态、弹射速度等对整个分离过程有很大影响[5]。上述特点增加了无人机投送的技术难度。为保障无人机、载机的安全,必须研究无人机安全分离的条件。

在研究初期,往往希望能够快速给出不同状态下投放物离机轨迹,研究安全分离边界,以确定方案是否成立[6]。该阶段往往使用计算准度满足一定要求的简便方法。这些简便方法通常是准定常方法[7],是把连续的非定常分离过程简化成多个时间间隔很小的定常状态进行研究的方法。此类方法计算量少,尽管无法准确计算出非定常效应,但是对于非定常效应不显著的情况可以快速给出投放物的分离轨迹。此类准定常快速方法又称为工程估算方法。

目前,典型的工程估算方法研究分为三类[8-19]：基于理论分析的、基于数值模拟(CFD)的和其他非典型方法。基于理论分析的典型工作有：1)范召林使用源汇模型和涡格模型模拟载机体积效应和法向力效应,考虑载机在投放物上产生的干扰速度分布[8]。采用当量迎角概念计算弹翼的气动力,但是该方法的一些假设和当量迎角中干扰因子的计算尚有待进一步验证[8]。与飞行试验相比,滚转角的模拟大约有10°的偏差。2)美国国家航空航天局采用细长体理论计算外挂物的气动特性,建立了分离仿真系统,给出了外挂物的分离轨迹[12]。由于细长体理论的限制,不能用于非细长体外挂物(如副油箱,无人机等)的分离轨迹研究。基于数值模拟的典型工作有：1)张启南使用数值模拟方法计算载机的非均匀流场,采用面元法与工程估算相结合的计算方法计算载机非均匀流场中投放物的气动力。计算一条分离轨迹只需30 min,但是同样存在对滚转角模拟较差的情况[9],与风洞CTS实验结果相比,投放物的滚转角大约存在40°的偏差。2)AEDC(arnold engineering development center)使用CFD结合工程方法预测了跨音速下投放物与战斗机的分离轨迹[13,17]。与飞行试验相比,在俯仰和偏航方向有较好的一致性,但是对滚转方向的姿态角存在大约12°的偏差。其他非典型方法有：1)高晓光基于流场角度轨迹技术的思想,将风洞试验得到的载机干扰流场制成数据库,根据外挂物的坐标值查询载机干扰流场,得到相应的流场系数,进而求得气动力和力矩系数,最终获得外挂物的运动状态;但只是将外挂物当做质点分析,定性的确定了干扰流场对外挂物姿态变化的影响,未做定量研究[10]。2)张冬云在均匀来流条件下计算了离机人员的阻力情况,并对人员的受力进行了假设和简化,建立了动力学模型,提出了较为简单的分离轨迹估算公式。但是将离机人员当做质点,且不考虑载机干扰流场的影响,只能进行简单的定性分析[11]。综上分析,目前已有的工程估算方法能够在研究初期快速给出分离轨迹,但获得的数据信息单一且准度较低。文中认为,分离轨迹估算准度偏低的重要原因之一是滚转角计算偏差较大。滚转角估计不准确将严重影响到投放物气动力估算的准确性,从而导致分离轨迹的工程估算结果可信度较低。

另外,在研究方案阶段,通常已分别获取了大量载机流场和无人机的气动性能数据,如果利用这部分数据进行轨迹预测,一方面不用增加额外的计算工作量,另一方面,又能够改进轨迹预测的准确性,这将是改进工程估算方法准确性的一种新思路。基于此,文中发展了一种基于双参考点的无人机分离轨迹高准度快速预测方法。其中双参考点取在无人机半模型的气动中心,考虑无人机左右流场的不均匀性带来的滚转力矩影响。经验证,该方法利用现有数据能够快速的计算无人机离机轨迹和姿态,结果满足工程应用要求。

1 计算模型和计算方法

1.1 轨迹预测方法

1.1.1 载机和无人机参数

针对载机投放无人机的安全分离问题开展分离轨迹的快速预测方法研究。投放位置的大气条件是海拔高度500 m、压力95 461 Pa、密度1.167 3 kg/m3、重力加速度9.805 1 m/s2、温度284.9 K;参考坐标系为载机坐标系O1X1Y1Z1,与载机固连,原点O1位于分离起始点;O1X1平行于载机轴线,指向载机尾部;O1Y1在载机对称平面内,垂直O1X1向上;O1Z1垂直于载机对称平面,指向左。无人机翼展0.3 m,外形为常规布局,其他参数见表1。

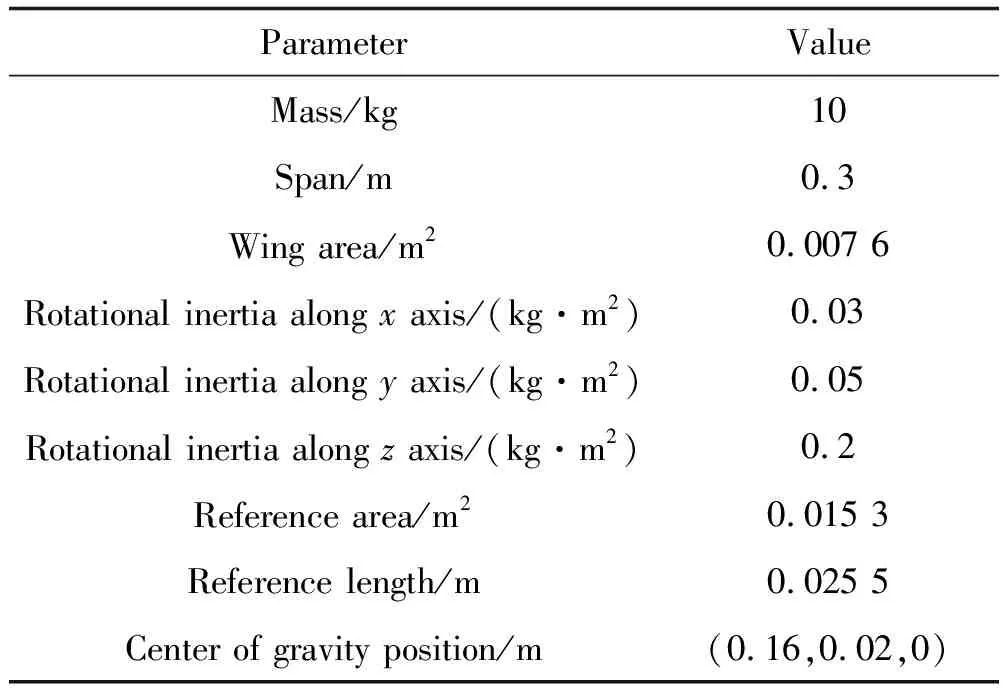
表1 无人机模型参数Table 1 UAV model parameters

载机翼展4.084 m,载机外形简化为机翼加机身,研究中载机流场计算条件选取飞行马赫数为0.45,载机的迎角为2°。无人机初始速度、初始位置和姿态(以下简称位姿)全部为0。

外挂物运动方程是包含3个旋转运动和3个平移运动的六自由度方程。为了便于研究外挂物的分离过程,文中定义无人机坐标系O2x2y2z2,与无人机固连,原点O2位于无人机质心;O2x2平行于无人机轴线,指向无人机尾部;O2y2在无人机对称平面内,垂直O2x2向上;O2z2垂直于无人机对称平面,指向左。文中在无人机坐标系下求解运动方程。将无人机轴系的轨迹和姿态变化通过坐标变换到载机轴系下表示。即分离轨迹结果均定义在载机轴系,可以直观分析无人机与载机的分离安全性。

1.1.2 分离轨迹快速预测方法流程

文中方法包含数据准备、无人机气流角和动压的计算以及六自由度方程的求解。

1)载机流场准备

基于求解RANS方程的CFD方法计算载机在给定来流条件下的干扰流场,计算结果如图1所示。

图1 载机干扰流场速度矢量图(α=2°,β=0°,Ma=0.45,H=500 m)Fig.1 Velocity cloud diagram of carrier interference flow field (α=2°,β=0°,Ma=0.45,H=500 m)

2)无人机气动特性模型的建立

在已有的CFD结果基础上,使用BP神经网络模型构建无人机气动性能数据库。样本数据为无人机在干净流场(无载机)下的气动性能CFD结果,计算条件如表2所示。

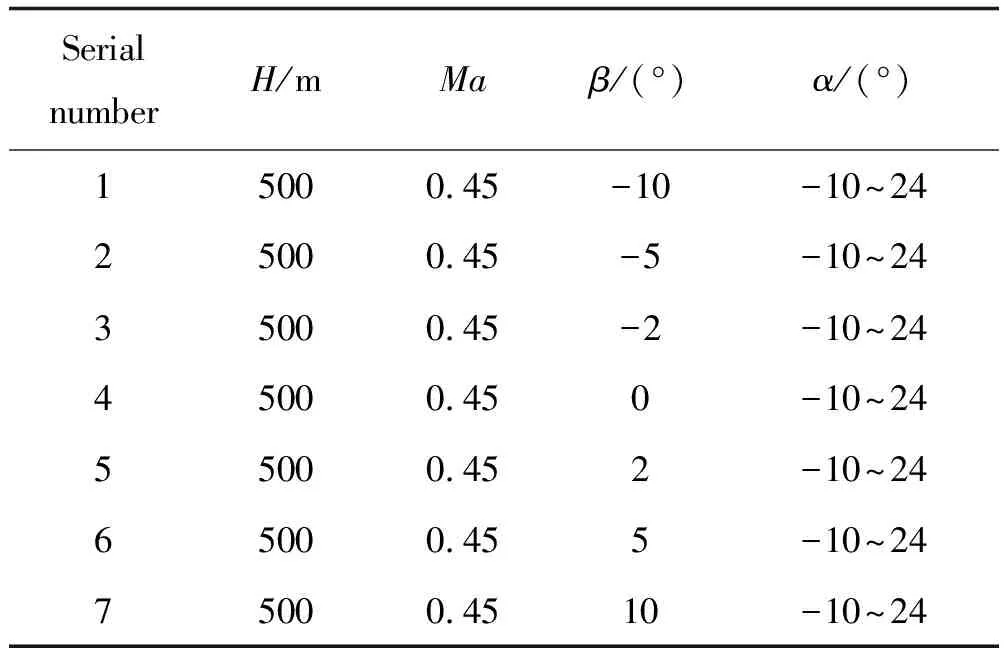
表2 无人机CFD计算状态参数变化Table 2 Changes in state parameters of UAV CFD calculation

由于载机流场中投放无人机的气动参数与迎角侧滑角之间没有精确的数学表达式,文中采用BP神经网络进行无人机气动参数的插值。

根据神经网络相关文献[19],隐藏层激活函数采Sigmoid函数,输出层激活函数采用Purelin函数。模型训练时,随机选择70%用于模型训练,15%用于模型验证,15%用于模型测试。预测误差如图2所示。

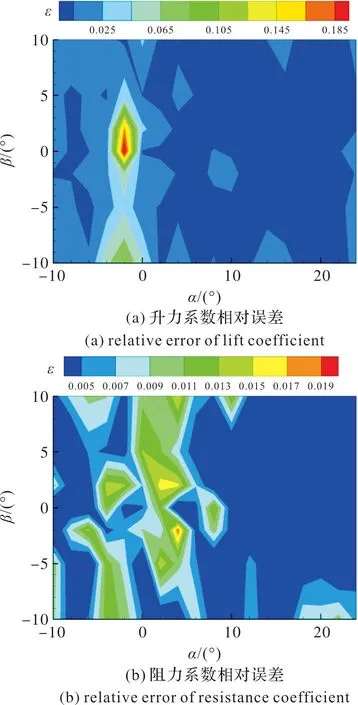
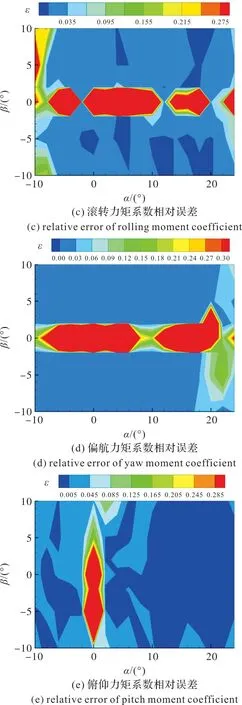
图2 BP神经网络模型预测误差Fig.2 Prediction error of BP neural network model

预测误差如图2所示。在大多数的迎角、侧滑角状态下,输出的气动力/力矩系数误差约为5%。当侧滑角为0°时,滚转力矩系数和偏航力矩系数非常小,接近于0;当迎角为0°时,俯仰力矩系数也非常小。因此这两类情况下的力矩系数相对误差显得稍大。可见,文中训练的神经网络模型预测误差小,满足快速预测方法需求。

3)六自由度运动方程求解

使用四阶Runge-Kutta方法[18]求解六自由度方程。

1.2 无人机参考点处气流角与动压的计算方法

研究有两个前提：1)无人机对载机流场的干扰量是小量。对于文中的投放情形而言,载机与无人机的展长之比为17∶1,可认为无人机对载机流场的干扰小,无人机附近的流场主要取决于载机流场。2)载机干扰流场的非定常效应不显著。无人机初始分离位置处于载机腹部下方,相对于机翼/机身后方的流场,涉及的流场相对平稳。无人机是以正常的姿态、零初始速度的自由投放。下面说明文中参考点位置的选取、气流角和动压的计算方法。

1.2.1 参考点位置选取

文中的参考点沿展向对称布置,如图3所示(下文简称双参考点),分别取考虑了无人机机翼和平尾等升力面影响的半模型气动中心。平均气动弦长的中点总是与机翼面积的中心相重合[20]。机翼的气动中心展向位置为0.075 m,平尾的气动中心展向位置为0.023 m。使用式(1)计算双参考点的位置：

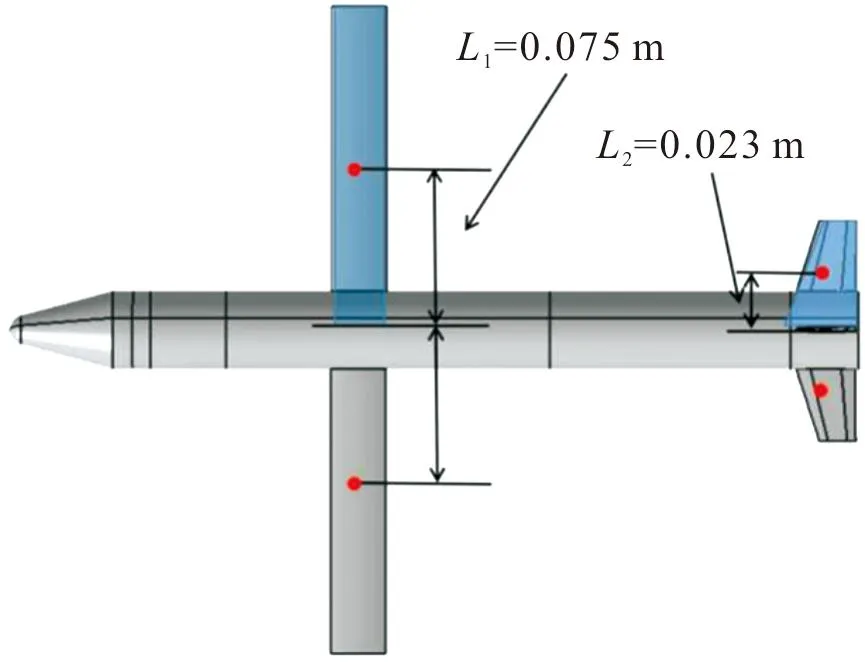
图3 双参考点位置示意图Fig.3 Double reference point position diagram

L=k1L1+k2L2

(1)

式中：L1为机翼气动中心展向距离;L2为平尾气动中心展向距离;k1,k2为机翼和平尾对参考点展向位置的权重系数。理论上,升力面的升力决定了k1,k2的大小,为了便于计算,使用式(2)、式(3)对k1,k2进行计算。

(2)

(3)

式(2)～式(3)中,S1和S2分别为机翼面积和平尾面积,S1=0.00764 m2,S2=0.00258 m2。经计算：k1=0.75,k2=0.25,L=0.062 m。

双参考点的x坐标取无人机机翼平均气动弦长的四分之一处,z坐标落在无人机坐标系O2x2z2平面。应该指出,文中的双参考点不是传统意义上的气动中心,而是经过研究确定的适用于轨迹快速预测的特征位置。

1.2.2 气流角和动压计算

分离轨迹快速预测方法的核心是载机干扰流场下无人机的气动力和力矩的确定,其关键是无人机气流角和动压的计算。

为了研究方便,首先考虑采用代数平均求取载机干扰流场中的气流速度V1的3个分量：

(4)

式中：n为参考域内的网格节点数;V1i为载机干扰流场中的气流速度V1的i方向分量,i=1,2,3(1表示x方向,2表示y方向,3表示z方向,下同);v1i,j为第j个网格点上速度v1的i方向分量。

定义无人机运动速度为V2,V2i(i=1,2,3)分别为V2的3个分量。无人机质心在载机干扰流场下的相对气流速度V3的3个分量的计算公式为：

V3i=V1i-V2i

(5)

由V3的分速度及合速度求得质心流动角,根据质心流动角和无人机姿态角求得气流角即无人机的迎角α、侧滑角β,两者可表示为：

α=θxy+θz
β=θxz+θy

(6)

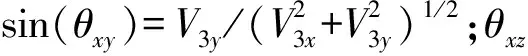
动压q可表示为：

(7)

式中ρ为自由来流空气密度。

偏差计算公式为：

(8)

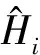
参考域大小对气流角、动压的影响如图4所示。黑色的线表示参考域大小对代数平均求取等效值的影响。参考域球体半径取值较小时,参考域内网格节点少,等效值波动较大;参考域球体半径较大时(R>0.15 m,无人机初始位置距离载机为0.15 m),参考域会与载机相交,导致等效值变化较大。当参考域球体半径在0.05～0.10 m时,迎角、侧滑角变化小于0.02°,速度大小变化小于0.01 m/s。因此,如果采用代数平均方式,参考域半径取为0.08 m是合适的。

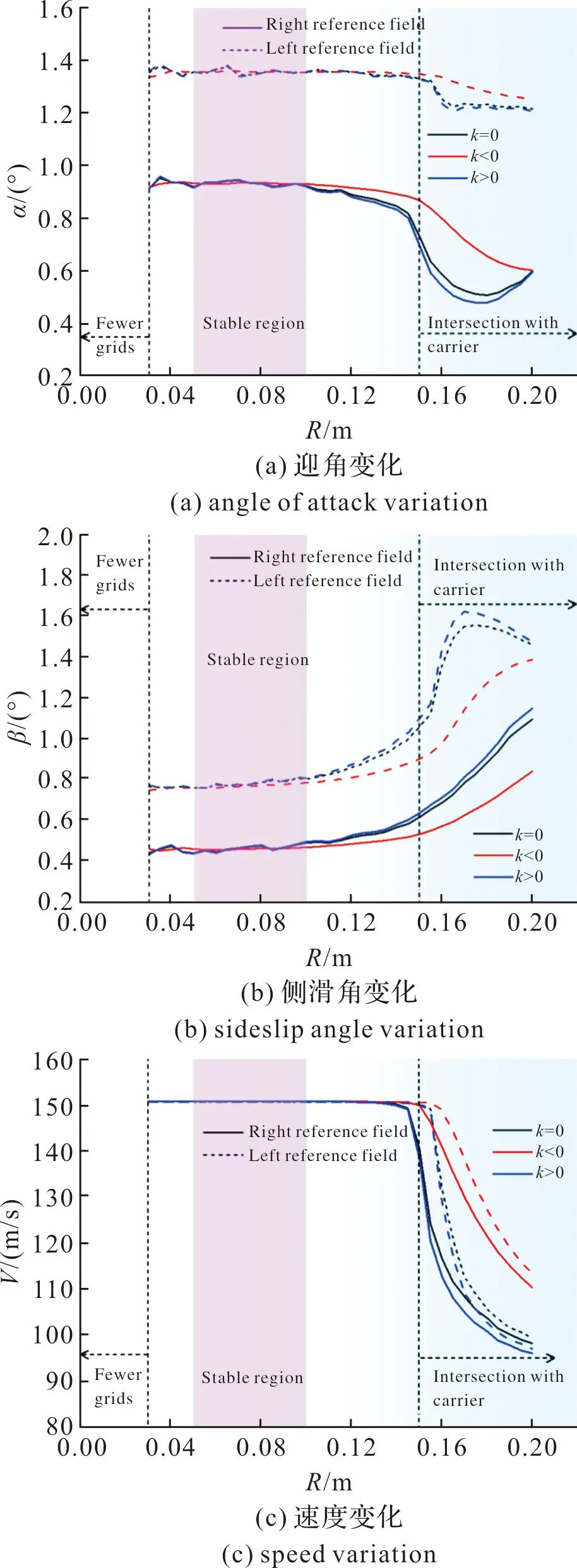
图4 参考域大小对气流角、动压的影响Fig.4 Influence of reference domain size on airflow angle and dynamic pressure

反比例权重和正比例权重方法对结果的影响如图4和图5所示。k=0为代数平均,k<0为反比例权重法,k>0为正比例权重法。由图4可知,红色的线更平稳,黄色的线更陡峭,但是不改变代数平均求取的稳定区域大小。

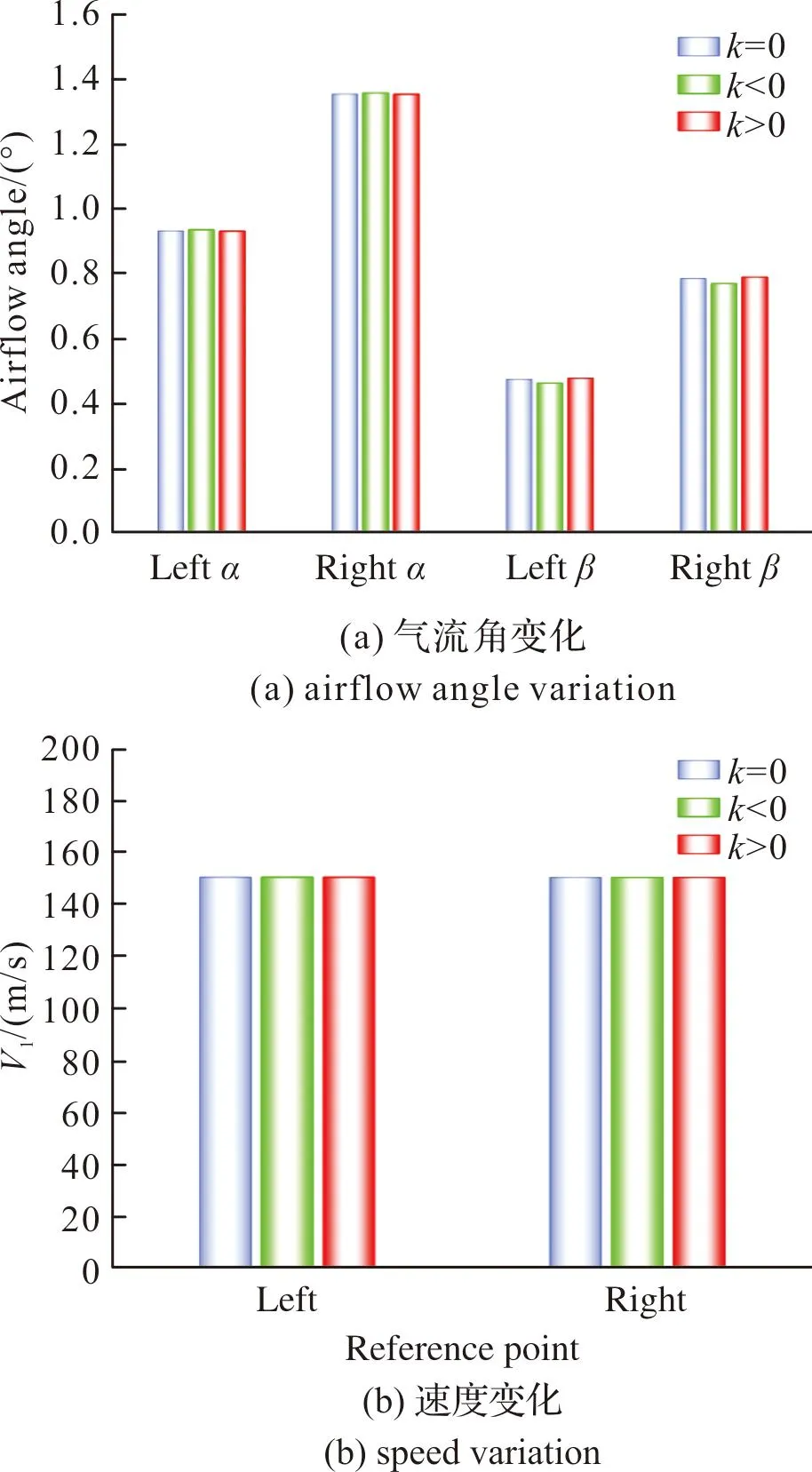
图5 不同加权方式对求取速度和气流角的影响Fig.5 Influence of different weighting methods on velocity and airflow angle

在参考域半径大小为0.08 m情况下,3种加权方式对求取速度大小和气流角的影响如图5所示。蓝色、绿色、红色的圆柱表示3种加权方式,对迎角的影响偏差最大不超过0.004°,对侧滑角的影响偏差最大不超过0.02°,对速度的影响偏差最大不超过0.01 m/s。可见,不同加权方式对等效气流角和速度的影响很小。因此,文中采用简单代数平均计算参考域内的等效气流角和速度。

2 计算结果与讨论

2.1 预测结果与CFD结果的对比

CFD计算采用URANS方法求解N-S方程得到给定时刻的分离物稳态干扰气动力,结合刚体6DOF方程得到分离物下一时刻位置和姿态角,通过嵌套网格,使空间网格适应分离物新的位置和姿态进入下一步气动力计算循环;最后,得到分离体的分离轨迹。通过该计算方法得到的计算结果,通过项目验收,与实际分离情况基本吻合,可用作工程估算方法的验证结果。CFD嵌套网格计算的无人机分离过程如图6所示。

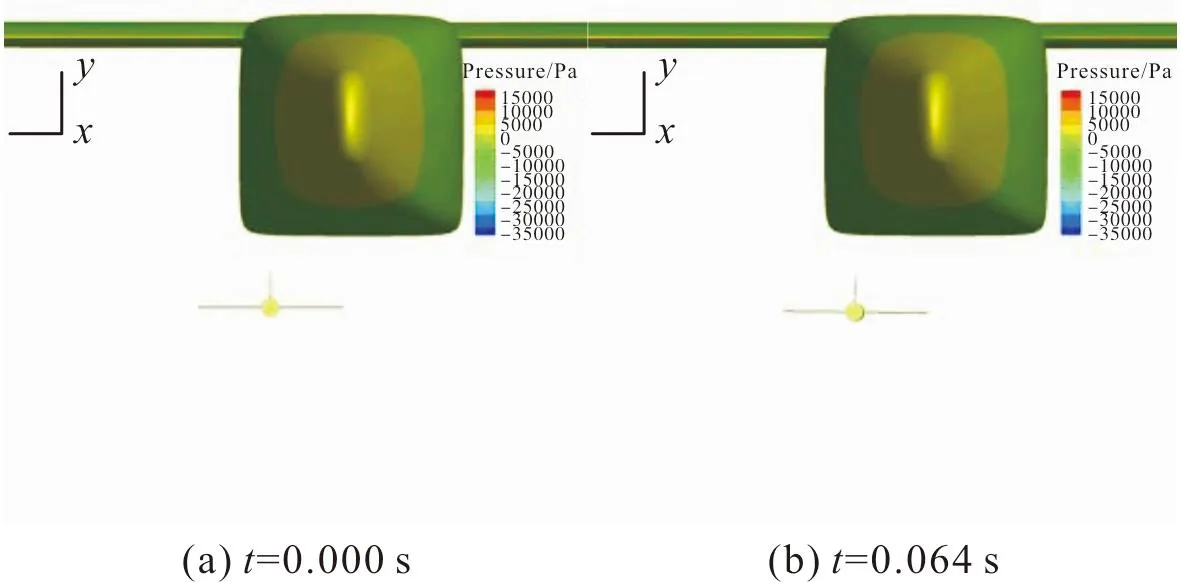
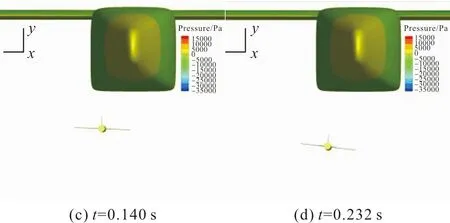
图6 CFD嵌套网格计算的无人机分离过程Fig.6 UAV separation process based on CFD nested Grid computing

文中方法得出的无人机分离轨迹与CFD嵌套网格计算的分离轨迹对比如图7所示。

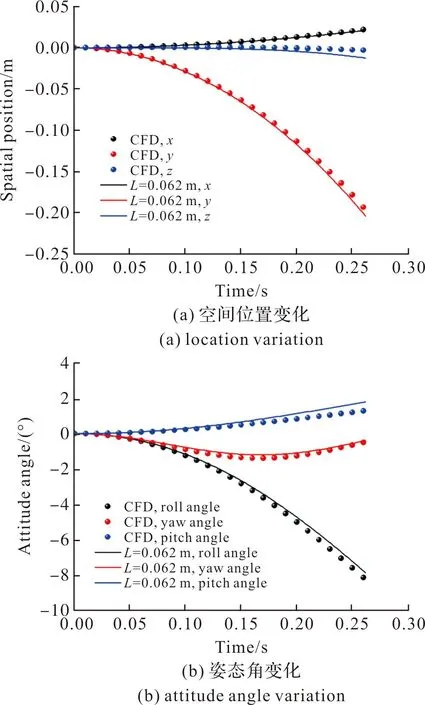
图7 快速预测方法与CFD计算结果对比Fig.7 Comparison between fast prediction method and CFD calculation result

由图7可知,预测结果与CFD计算结果趋势一致,准确的得到了无人机分离过程的空间位置和姿态角变化。采用文中发展的预测方法计算的结果满足工程要求。

2.2 参考点位置的影响

为了定量评价文中方法的预测偏差,进一步验证文中求取参考点位置的合理性,文中将参考点位置范围扩大为由无人机质心到翼尖,参考点在不同展向位置时轨迹预测的偏差如图8所示。图8(a)为空间位置偏差,图8(b)为姿态角偏差。黑色实线、红色实线和蓝色实线分别表示x,y,z方向的位置和姿态。空心球表示质心参考点(单参考点)、实心球表示使用2.2节方法计算的双参考点。

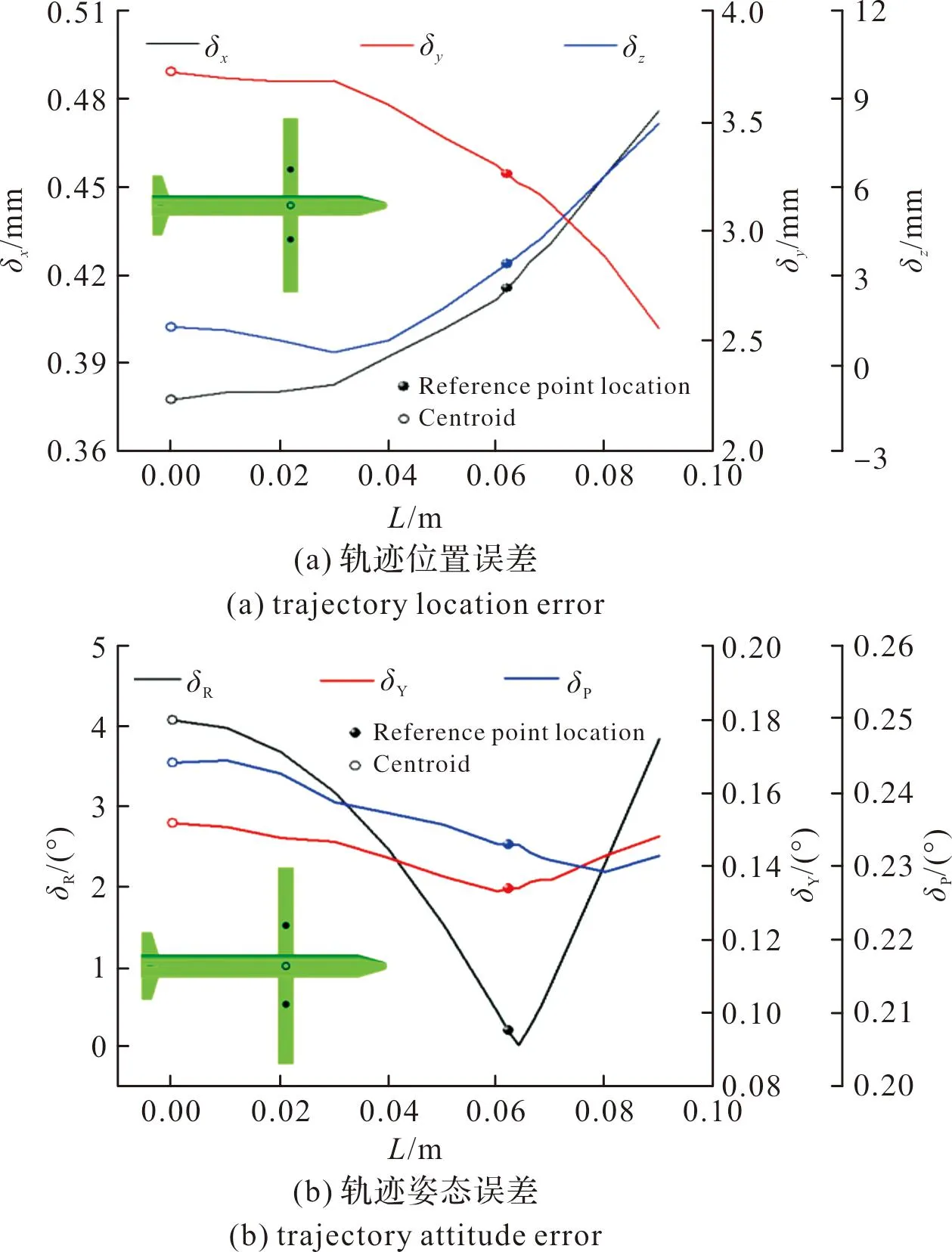
图8 不同展向位置的参考点预测分离轨迹姿态误差Fig.8 Reference points at different spanwise positions predict separation trajectory posture error

图8(a)中双参考点较单参考点的x方向位置偏差增大了3.8×10-5m,y方向位置偏差减小了4.6×10-4m,z方向位置偏差增大了2.1×10-3m。可见,参考点展向位置的变化对轨迹的空间位置偏差影响较小。图8(b)中双参考点较单参考点的滚转角最大相对偏差从103%降低到3.4%,预测精度有了数量级上的提升,偏航角最大相对偏差从51.2%降低到16.5%,俯仰角最大相对偏差从43.1%降低到38.4%。可见,双参考点较单参考点能更好的预测无人机的姿态角,尤其是滚转角。

文中方法较CFD方法耗时大大减少。在目前主流商用计算机上运行该算法,从导入数据到获得完整分离轨迹,文中的方法只需约120 s;而CFD方法给出一条完整分离轨迹需要3～5 d。当计算几十甚至上百个分离状态时,相较于CFD方法,该方法节省的时间将更可观。

3 结论

发展了一种基于双参考点的无人机离机轨迹和姿态高准度快速预测方法,解决了传统预测方法对滚转角预测精度不高的不足,满足研究初期快速获得大量分离轨迹、确定安全边界、制定后续实验与计算方案的需求。得出以下主要结论：

1)以无人机左右两部分的气动中心为参考点,考虑无人机左右机翼附近干扰流场的影响,计算由于流场的不对称产生的滚转气动力,对滚转角的预测由传统方法的103%降低到3.4%,预测精度有了数量级上的提升。

2)较以往取质心处的流场信息发展的方法,文中以双参考点为球心建立球形取值空间,通过区域内多个数据的平均,增加了数据的平稳性和准确性,克服了采用单参考点数据随机误差大的缺陷。