轮式底盘耦合下导弹发射装置跟踪控制方法及应用

姜晓明，刘宜罡，牛远征，殷 翔

(上海机电工程研究所，上海 201109)

0 引言

弹、站、架一体的导弹发射装置提高了防空导弹武器的单车作战能力,随着防空导弹装载数量的增多,导弹发射车(或称“战车”)的满载惯量也越来越大。当战车处于非支撑状态或机动发射状态时,战车底盘不能作为一个刚体,导弹发射装置加减速时的惯性运动将反作用于底盘,与底盘产生耦合运动,这种耦合运动对伺服系统稳定性的影响容易被忽略。

在已有文献中,一般从动力学角度分析战车机动和发射工况下底盘悬架和结构柔性对弹炮发射的影响。文献[1]分析了某轻型高机动平台油气弹簧悬挂特性对某高炮射击密集度的影响。文献[2]从发射动力学的角度分析悬架对火炮射击精度的影响。文献[3-4]从发射和车辆机动的角度给出了导弹发射车悬架的优化设计和控制方法,以此来减小导弹的出筒振动响应。文献[5-6]研究了行车和导弹发射工况下车体振动控制和振动对导弹姿态的影响。文献[7-11]从发射动力学的角度分析了导弹发射装置柔性环节对导弹出筒姿态的影响。文献[12-13]发现当前的导弹发射装置伺服系统较少考虑底盘柔性影响,主要集中在发射装置的伺服控制方法研究方面。在底盘和上装设计中都需要考虑底盘谐振的影响,文献[14]通过电液主动悬挂可以有效衰减车体在1～10 Hz频率范围内的垂向振动,文献[15]给出了动力总成的设计要求之一是其固有频率应该避免与车身固有频率重叠。

此外,已有文献较少考虑底盘悬架在导弹发射装置跟踪瞄准过程中对上装的影响。当战车没有刚性支撑时,大惯量导弹发射装置的运动会与底盘相互作用,引起车体姿态变化,这种变化会耦合到发射装置的伺服控制中。大惯量发射装置调转跟踪对底盘的反作用力影响无法忽略,会引起发射装置跟踪的不稳定。针对上述问题,文中建立耦合底盘悬架的发射装置伺服控制模型,分析底盘耦合特性对发射装置跟踪运动的影响,采取相应的设计措施,对底盘的耦合影响进行抑制。

1 底盘悬架耦合的发射装置动力学模型

1.1 底盘模型

战车采用独立油气悬架,从力的传递关系分析,路面激励经过轮胎、悬挂、车架(副车架)等传递到发射装置的回转支撑,再由回转支撑传递到整个发射装置。不失一般性,从车尾方向看,悬架系统、轮胎等效为弹簧阻尼系统,如图1所示,左侧车桥悬架等效为k1,c1,右侧车桥悬架等效为k2,c2,导弹发射装置回转支撑位于左右车桥之间,底盘与上装组合体的质心为O,组合体沿着车体滚动方向的转角为θ,组合体在车体滚动方向的转动惯量为J1。左侧悬架到质心的距离为L1,右侧悬架到质心的距离为L2。导弹发射装置在方位和高低方向上可以完成瞄准和跟踪运动,发射装置在高低调转和跟踪过程中,产生的惯性力反作用于车架,会使整车产生侧倾力Fr,侧倾力作用点到质心的距离为L3。

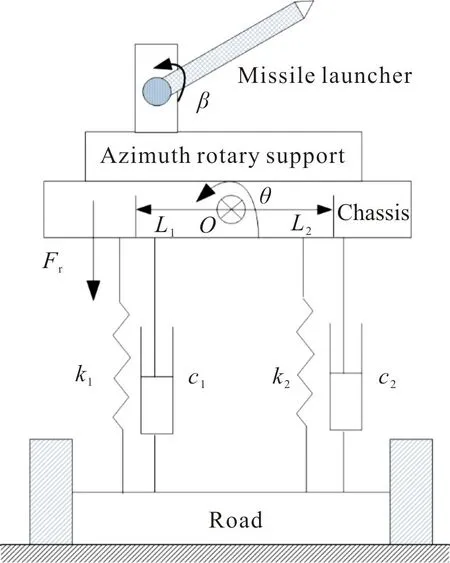
图1 底盘悬架与发射装置组合体示意图Fig.1 Schematic diagram of the chassis suspension and the missile launching equipment

以战车自平衡位置为原点,令初始状态θ0=0,战车在滚动方向受发射装置调转产生的反作用力后,会沿着滚动方向发生侧倾,其动力学方程描述为：

(1)

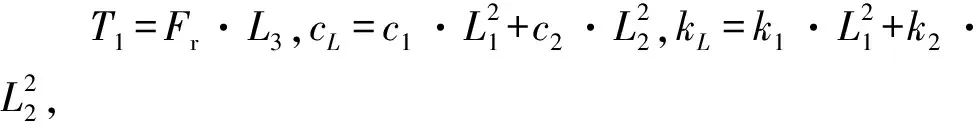
(2)

1.2 含底盘特性的发射装置控制系统

考虑发射装置与底盘的相互作用时,发射装置控制系统的结构框图如图2所示。其中,K1为位置控制器,K2为速度控制器,Ge为电流环传递函数,电机及传动机构生成的力矩T2除了驱动发射装置力矩-位置传递函数P完成运动外,还通过力矩几何关系传递系数k(k<0)生成反作用于底盘V的力矩T1,该力矩产生的底盘航向姿态角X和目标指向R1经过坐标变换矩阵M得到车体系下的作用指令R2。如果底盘通过支撑作用简化为刚性环节,则发射装置生成的反作用力不会产生明显的车体姿态变化,不需要进一步分析底盘对发射装置跟踪过程的影响。如果底盘为非支撑柔性环节,则需要进一步分析其影响。

图2 考虑底盘特性的发射装置控制框图Fig.2 Control block diagram of the launcher considering chassis characteristics

令地理系下的目标指令R1为(R,A,E),R为目标斜距,A为目标方位角,E为目标高低角,底盘的航向角为φ,横滚角为ψ,俯仰角为ε,目标指令在直角坐标系下的表达形式为：

(3)

式中：x1为东向分量;y1为北向分量;z1为垂向分量。从地理系转换到车体系直角坐标下的目标指令为：

(4)

式中：a21=-sinφcosε-cosφsinψsinε;a22=cosφcosε-sinφsinψsinε;a31=sinφsinε-cosφsinψcosε;a32=-cosφsinε-sinφsinψcosε。

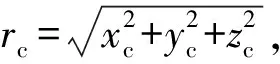
(5)

为便于分析导弹发射装置的高低运动与车体滚动姿态之间的相互影响,简化3个车体姿态角在模型中的耦合,令底盘的航向角φ为0°,即：车头指向正北,俯仰角ε为0°,则式(4)变为：

(6)

在3个姿态角耦合的状态下,除了发射装置指向车头外,车体滚动方向和发射装置高低方向的相互影响仍然存在。不失一般性,当目标初始飞行方向为90°时,即：A=90°,则车体的高低角Ec=E-ψ,此时发射装置的目标方位指向与车头指向相差90°,发射装置在高低方向上的调转直接作用在车体的滚动方向上。在车体滚动方向(即发射装置在高低方向)上,考虑底盘滚动角的影响,发射装置在高低方向上的控制框图如图3所示。在传统基于车体系的发射装置控制回路中,考虑了车体滚动姿态角的影响,增加了车体稳定回路。此时,车体稳定回路在发射装置基于地理系的跟踪回路中起到了正反馈作用,将对发射装置高低方向上伺服系统的稳定性产生影响。

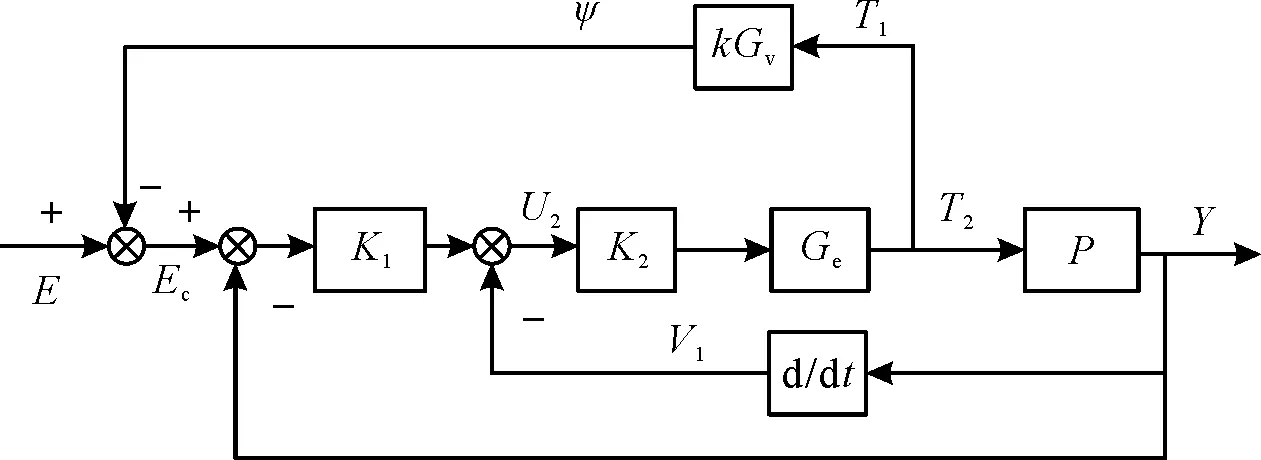
图3 考虑底盘滚动特性的发射装置控制框图Fig.3 Control block diagram of the launcher considering chassis rolling characteristics

2 耦合底盘的发射装置影响分析

2.1 系统稳定性分析

对图3进一步分析,令发射装置的闭环位置反馈系统为Gr,反馈回路中发射装置反作用到底盘的力矩-位置传递函数(简称“底盘传递函数”)Gv1=-kGv,发射装置力矩-位置传递函数为P,则此时系统等效为图4所示的正反馈控制系统。系统的稳定性与Gr和Gv1/P的性质相关。下面对发射装置伺服系统在柔性底盘下的稳定性进行分析。为保证系统是稳定的,在地理系下的稳定控制回路中增加跟踪滤波器Gf,如图4所示。

图4 发射装置与底盘等效控制框图Fig.4 Simplified control block diagram of the launcher and the chassis

证明：

令B=Gf×Gv1/P,则E到Y的传递函数为：

(7)

由于Gr和Gv1都是稳定的,则BGr无右半平面的极点,根据奈奎斯特判据：当Re(-BGr)>-1时,则系统是稳定的,即：当Re(BGr)<1时,系统是稳定的。

令ρ为BGr的幅值,则：

通过发射装置位置闭环设计,容易保证发射装置伺服系统闭环传递函数Gr是稳定的,通过1.1节底盘悬架系统的结果得到Gv1是稳定的,因此在工程设计中可以找到滤波器Gf,通过抑制悬架阻尼来实现系统的稳定。

2.2 底盘谐振辨识与滤波器设计

通过实验获取战车导弹发射装置高低调转运动对底盘姿态的影响,当发射架进行加速减速时,会对底盘产生较大的反作用力,此时,底盘在强迫振动下的横滚角运动曲线如图5所示。

图5 底盘的谐振特性Fig.5 Resonance characteristics of the chassis

受底盘悬架阻尼的影响,车体在滚动方向经过2～3 s后逐渐收敛。基于式(2)中战车底盘受力到车体滚动角的推导结果,利用最小二乘法拟合对式中系数进行辨识,得到含力矩传递系数的底盘谐振传递函数Gv1为：

(8)

上述底盘的传递函数表明在发射装置的反作用力下,底盘在滚动方向上存在1.94 Hz的谐振点。为了消除底盘与发射装置之间的耦合谐振,抑制底盘谐振的影响,设计陷波结构形式的滤波器,对车体姿态中的滚动角进行滤波,滤波器中心频率为底盘的谐振频率1.94 Hz,在谐振频率处的衰减系数为0.1,则设计的滤波器为：

(9)

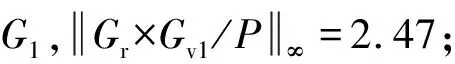
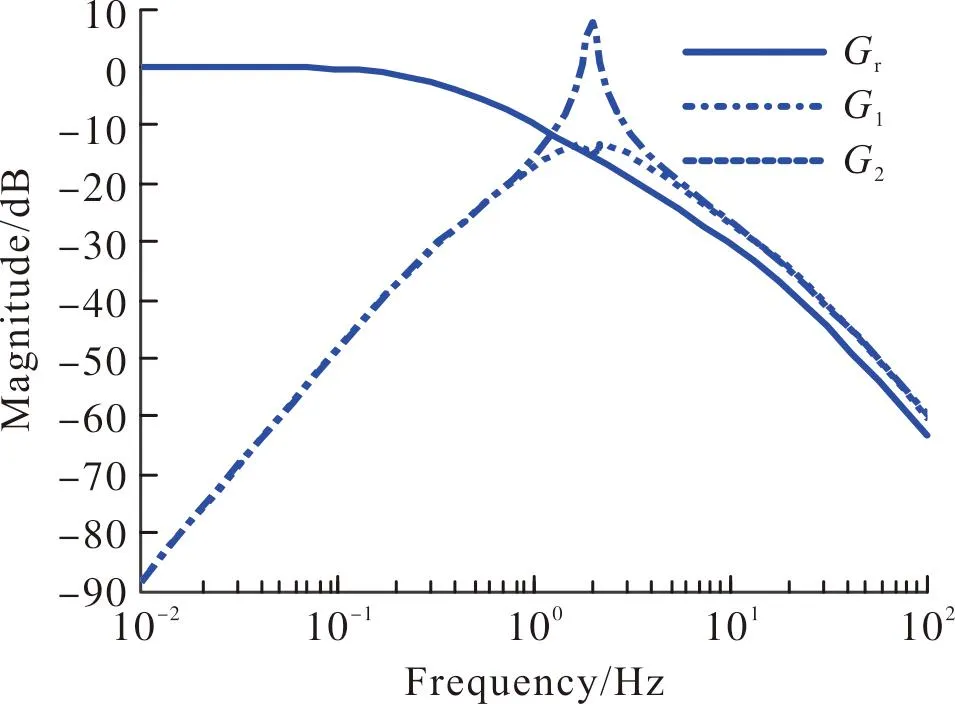
图6 系统开环幅值特性Fig.6 Open-loop amplitude characteristics of the system

3 仿真与试验

当不考虑底盘谐振时,发射装置闭环控制系统是稳定的,如图6中的Gr所示。

在图5所示的底盘谐振作用下,通过仿真得到发射装置的跟踪曲线如图7所示,在未增加跟踪滤波器Gf时,图中λ1所示的发射装置跟踪曲线是发散的,系统是不稳定的;当增加跟踪滤波器Gf后,图中λ2所示的发射装置跟踪曲线是稳定的。实际上,尽管通过降低发射装置闭环系统Gr的带宽,可以实现系统的稳定,但却牺牲了发射装置的跟踪性能,因此通过设计抑制底盘谐振的陷波滤波器是系统稳定且能保证性能的一种有效技术手段。

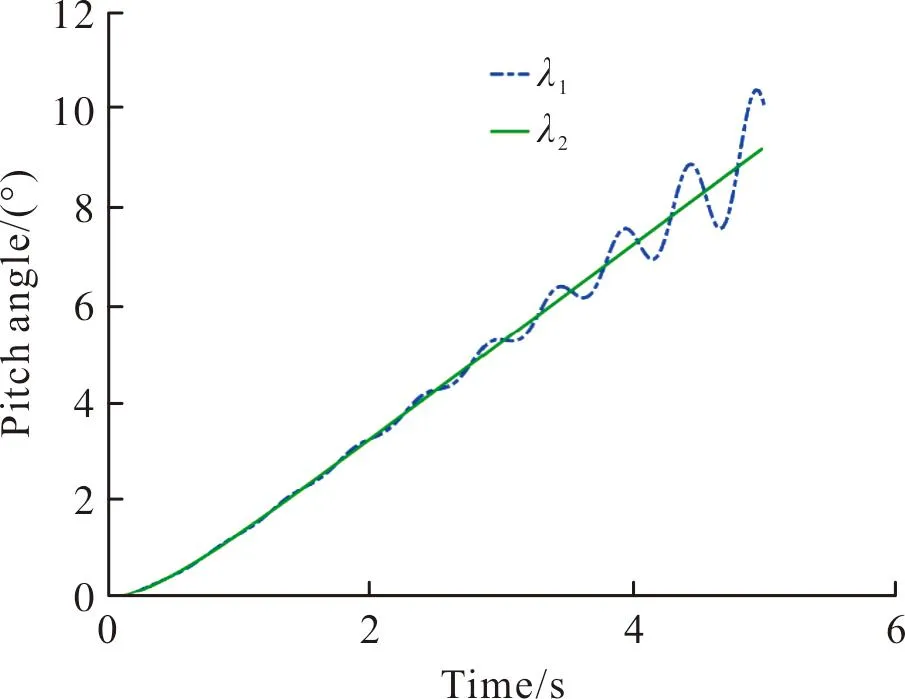
图7 发射装置仿真跟踪曲线Fig.7 Simulation tracking curves of the launcher

将文中的设计方法应用于战车发射装置,在不加滤波器之前,发射装置在高低方向发生共振,调转到固定角度时的跟踪曲线如图8(a)所示,图中Y1为车体系下的高低角,Y2为地理系下的高低角,R为地理系下的目标高低角,发射装置的高低角产生幅值为0.5°的震荡,与底盘发生了共振。在施加抑制底盘谐振的跟踪滤波器Gf后,发射装置实现了稳定跟踪,跟踪曲线如图8(b)所示,Y是实际的高低角,车体系下发射装置目标高低角(耦合了车体横滚角)和实际高低角都逐渐收敛稳定,说明提出的方法是有效的。

图8 发射装置跟踪误差曲线Fig.8 Tracking curves of the launcher

4 结论

对非支撑状态底盘柔性耦合下发射装置伺服系统的稳定性进行了分析,给出了考虑底盘悬架特性时发射装置伺服系统的控制模型和系统稳定性条件,通过对车体姿态的滤波来抑制底盘悬架的影响,在运动负载一定范围内实现了导弹发射装置伺服控制系统在柔性底盘下的稳定性。