基于结构设计的陀螺加速度计温度系数补偿方法

周晓俊，凌林本，杨功流，李 亮

（1.北京航空航天大学仪器科学与光电工程学院，北京 100191；2.北京航天控制仪器研究所，北京 100039）

摆式积分陀螺加速度计（Pendulous Integrating Gyro Accelerometer,PIGA）简称为陀螺加速度计，是一种利用陀螺力矩平衡惯性力矩的摆式加速度计[1,2]，具有精度高、量程大、抗干扰强和能自动积分等优点，为平台式惯性测量系统的核心仪表[3,4]，主要用于测量载体相对惯性空间的加速度，广泛应用于国内外战略武器惯性导航系统中[5,6]。

在平动基座下，陀螺加速度计的误差模型可写为式(1)所示[7-12]：

式中，α˙为仪表进动角速度，即仪表的输出；aX为输入加速度；K0为与加速度无关的零次项系数，即偏置误差；K1为与加速度成比例的一次项系数，即比例系数；K2为与加速度平方有关的二次项系数；η为输出随机误差。通常用一次项系数1K的稳定性作为衡量加速度计精度的指标。对于陀螺加速度计而言，一次项精度主要与仪表的摆性和角动量的稳定性相关。

液浮陀螺加速度计是目前国内外工程应用上能实现的最高精度的加速度计[13,14]，其内环采用全液浮支承方式，浮子重力由浮油的浮力来平衡，可有效减小仪表内环干扰力矩的影响，从而实现高精度。其结构示意图如图1所示。

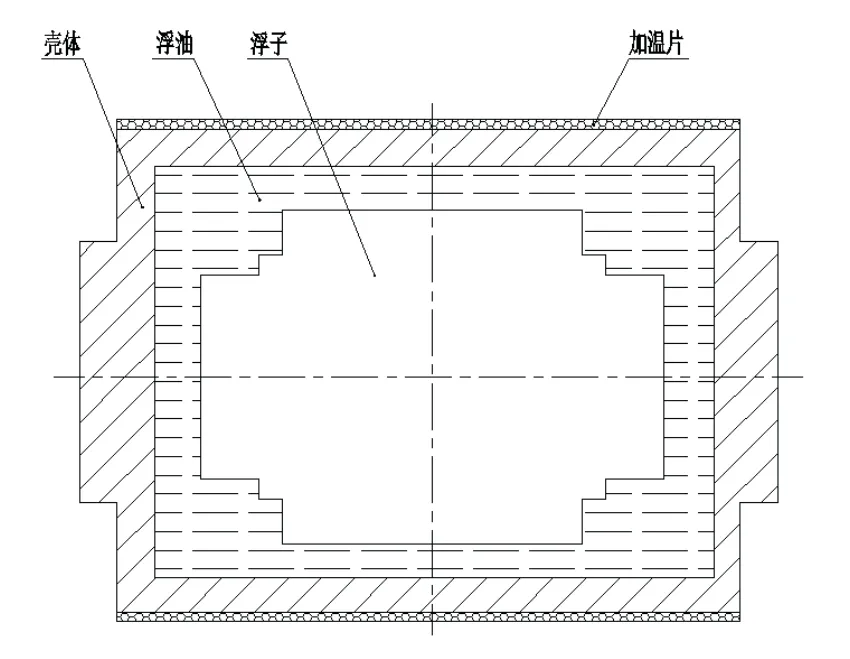
图1 液浮陀螺加速度计结构示意图Fig.1 Structural representation of the liquid floated gyro accelerometer

在图1 中，仪表内部充满高比重的浮油，而浮油的密度与温度密切相关，因此，通过加温片加热可以调整仪表的温度，进而改变浮油的密度。当达到一定温度（仪表工作温度点）时，浮油产生的浮力刚好与浮子的重力平衡，即可使得浮子完全悬浮于浮油中。此外，对于高精度的陀螺加速度计而言，仪表摆性和角动量随温度的微小变化也会造成仪表精度的变化。因此，可以看出，温度对液浮陀螺加速度计的性能至关重要。

为此，提高液浮陀螺加速度计的精度，必须减小仪表的温度误差[15,16]，主要从两方面进行：一方面，可以提高仪表的温控精度，使得仪表内部的温度场尽量均匀，减小温度梯度；另一方面，也需控制仪表的温度系数，即减小仪表一次项随温度变化的灵敏性。通过技术攻关，某型液浮陀螺加速度计的温控精度已由±0.3℃提升至±0.03℃[17]，在仪表温度系数不变的条件下，很难进一步减小温度误差，进而难以提升仪表的精度。因此，通过采取结构设计补偿的方法来减小仪表温度系数，是进一步提升液浮陀螺加速度计精度的有效途径。

国内研究人员在设计上对液浮陀螺加速度计一次项温度系数的控制方面考虑较少，一般只是简单的采取线膨胀系数小的合金来作为陀螺电机和浮子组件的材料，而对材料线胀系数匹配和仪表温度系数补偿设计等方面的研究资料非常少。某型液浮陀螺加速度计的一次项温度系数实测数据大于1×10-5/℃，仅温度波动对仪表的精度误差超过了3×10-7，这对高精度陀螺加速度计来说，显然温度误差太大，需加以控制。

1 温度系数计算

陀螺加速度计的原理示意图如图2所示[18]。

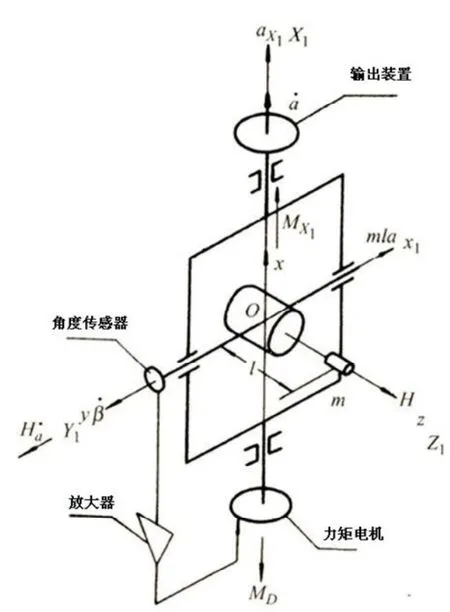
图2 陀螺加速度计原理示意图Fig.2 Schematic diagram of PIGA principle

在转子轴（Z轴）上距中心距离为l处存在一个偏心质量m，形成仪表的摆性ml；陀螺电机沿转子轴（Z轴）高速稳定旋转，提供角动量H；当沿输入轴（即外环轴，X轴）有输入加速度aX作用时，由于仪表摆性ml的存在，将在输出轴（即内环轴，Y轴）上产生偏摆力矩mlaX；根据陀螺原理，在此力矩作用下，陀螺加速度计将绕外环轴（X轴）进动，其进动角速度α˙与输入加速度aX成正比；而当仪表以α˙进动时，在内环轴（Y轴）上便会产生陀螺力矩Hα˙，此陀螺力矩与偏摆力矩相平衡：

因此，根据陀螺加速度计误差模型，一次项系数K1可写为式(3)所示：

由于构成仪表摆性ml和角动量H的零组件采用的结构材料不同，其线膨胀系数存在一定差异。当存在温度变化或温度梯度时，摆性ml和角动量H随温度的变化量不一致，将造成液浮陀螺加速度计的一次项发生变化。因此，将液浮陀螺加速度计一次项对温度的敏感程度定义为一次项温度系数，其表征：温度变化1℃，仪表一次项K1的相对变化量，计算公式如式(4)所示：

式(4)中，α为一次项温度系数，ΔK1为仪表一次项K1的变化量，Δml为摆性的变化量，ΔH为角动量的变化量。

此外，定义摆性的温度变化率为αl，角动量的温度变化率为αr，分别如式(5)(6)所示：

将式(5)(6)代入到式(4)，那么一次项温度系数可进一步写成式(7)：

1.1 摆性温度变化率αl计算

液浮陀螺加速度计的摆性变化可以由作用于陀螺组件上力的投影变化引起，也可以由摆性臂长的变化引起。在静基座试验时，摆性温度变化率可以由式(8)表达：

式(8)中，mi为构成浮子摆性的第i个零件质量，il为第i个零件的质心距浮子中心的距离。

由于质量m随温度的变化可以忽略不计，而摆长l的变化主要由零件材料线膨胀系数和零件温度变化所确定。因此，式(8)可进一步写作为：

式(9)中，αi为第i零件的线膨胀系数。

在某型液浮陀螺加速度计浮子结构中，构成摆性的零组件包括支架、马达和偏心配重等。摆性温度变化率αl计算公式为浮子中上述零件的线膨胀系数对摆性的加权和。根据浮子的实际参数，可计算得到液浮陀螺加速度计浮子的摆性温度变化率为αl=11.21 ×10-6/℃。

1.2 角动量温度变化率αr计算

液浮陀螺加速度计的陀螺电机采用内转子式半球型动压气浮马达，工作时在气体环境中高速稳定旋转，提供仪表的角动量。角动量的计算公式如式(10)所示：

式(10)中，J为马达转子转动惯量，ωr为马达转速。

在静基座试验时，角动量的变化可以由式(11)表达：

式(11)中，Jj为构成马达角动量的第j个零件的转动惯量。

由于马达质量和马达转速ωr随温度的变化可以忽略不计，那么，角动量的温度变化率αr可由式(12)表达：

式(12)中，rj为构成马达角动量的第j个零件的惯性半径，mj为第j个零件的质量，αj为第j零件的线膨胀系数。

某型液浮陀螺加速度计角动量主要由马达球碗、惯量环和磁钢环等组成。α r的计算公式则为马达转子组件中每个零件的线膨胀系数对转动惯量的加权和。根据马达转子的实际参数，可计算得到液浮陀螺加速度计角动量温度变化率为αr=11.15 ×10-6/℃。

1.3 一次项温度系数计算

根据式(7)可得液浮陀螺加速度计一次项温度系数为式(13)：

液浮陀螺加速度计一次项的温度系数大于1×10-5/℃，以温控精度为0.03℃计算，则温度变化1℃将带来的一次项K1变化3×10-7，这对高精度陀螺加速度计来说，显然温度误差过大，需加以控制。

2 温度系数补偿方法

在上述分析过程中可知，摆性温度变化率和角动量温度变化率均与零件材料自身的线膨胀系数有关。因此，通过采用材料线膨胀系数匹配的方法，可在一定程度上减小仪表的一次项温度系数。但在液浮陀螺加速度计结构设计时，零组件的材料还需综合考虑：尺寸、重量、结构刚度、热传导情况、电磁性能等因素，因此，材料线膨胀系数匹配的方法无法完全将温度系数降低至零，还需研究其他的补偿方法。本文提出一种基于结构设计的陀螺加速度计一次项温度系数补偿方法，在浮子结构上去除一定量的体积，调整浮子质心与浮心距离浮子中心的距离，利用浮油作用到浮子上的浮力随温度的变化，来补偿仪表摆性温度变化率和角动量温度变化率的不匹配量。

液浮陀螺加速度计浮子结构为非对称设计时，浮子的质心、浮心位置如图3所示。工作状态时，浮子悬浮于浮油中，浮力等于重力，平衡公式如式(14)：

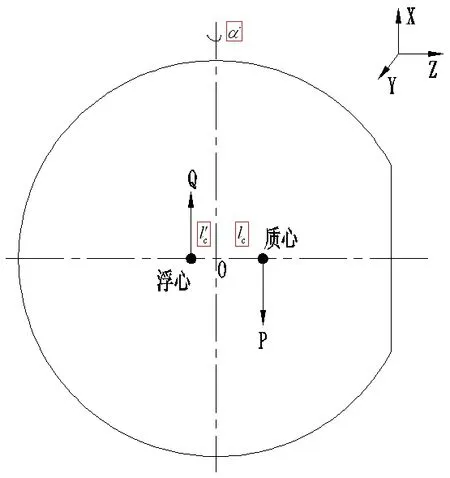
图3 浮子受力示意图Fig.3 Force diagram of float

式(14)中，P为浮子的重量，Q为浮油的浮力，ρ0为浮油在工作温度下的密度，V为浮子的体积。

根据液浮陀螺加速度计的工作原理，可建立内环轴（Y 轴）的力矩平衡方程，如式(15)：

式(15)中，lc为浮子质心偏离中心的距离，为浮子浮心偏离中心的距离。

由此，可进一步写成：

当仪表温度发生变化时，进动角速度的表达式可写为式(17)：

式(17)中，α0为浮子体积变化的等效线膨胀系数，0β为浮油的体膨胀系数，T为温度变化。

忽略含有线膨胀系数乘积项的小量，则确定相对进动角速度的温度变化表达式为：

在初始温度和保证“悬浮”的条件下（式(14)），温度误差补偿通过采用浮子结构体积不对称形状的设计方法来实现，令式(18)中所需的体积不对称量为，式(18)左边等于零，整理可得：

则补偿条件可写为式(20)的形式：

将某型液浮陀螺加速度计的相关设计参数代入式(20)中，可得补偿的体积不对称量数值为：

3 体积补偿设计

通过上述分析与计算，为补偿某型液浮陀螺加速度计的一次项温度系数，需要在浮子组件外围，沿摆性相反的方向进行体积补偿，补偿量为V′·l′=-844.24mm4。

在液浮陀螺加速度计浮子组件的结构设计中，一般采用沿马达轴（Z 轴）方向为偏心设计，从而形成仪表的摆性，而另外两个方向外环轴（X 轴）、内环轴（Y 轴）为对称设计。因此，进行体积补偿设计时，可以在Z 轴方向上进行去量调整，且去的量需尽量沿X 轴和Y 轴对称。

根据某型液浮陀螺加速度计的结构特点，在浮子组件的内环轴（Y 轴）两端对称位置，沿马达轴（Z轴）负方向，在半径为R的圆上，距离中心点L处，去除2 个长为B的弧形段，如图4 中阴影部分所示。

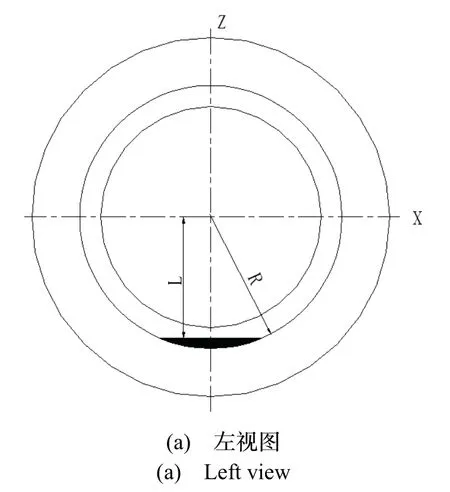
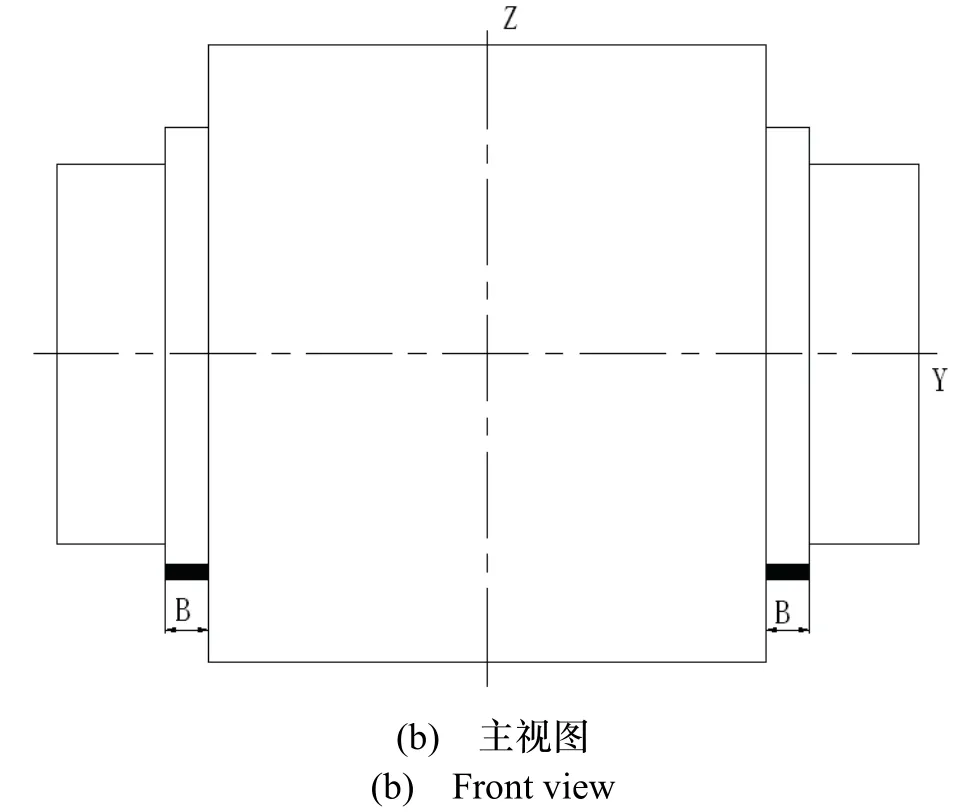
图4 浮子体积补偿设计Fig.4 Compensation design of the float

阴影部分的体积V0计算为：

则，体积补偿量为：

将某型液浮陀螺加速度计的结构参数：R= 13mm，B=3.4mm，V′·l′=844.24mm4代入式(23)可得：L=11.63mm。即在半径为13 mm 的圆上，距离中心点11.63 mm 处，去除2 个长为3.4 mm 的弧形段。

上述结构补偿设计，仅在Z 轴方向上进行去量，且沿X 轴和Y 轴对称，对陀螺加速度计的影响仅为增大了摆性的常值，增大量为1.5%，对浮子组件的结构刚度和稳定性的影响可忽略。

4 试验验证

对采取一次项温度系数补偿设计后的液浮陀螺加速度计进行温度系数试验验证，补偿设计前和补偿设计后的测试结果如表1所示。

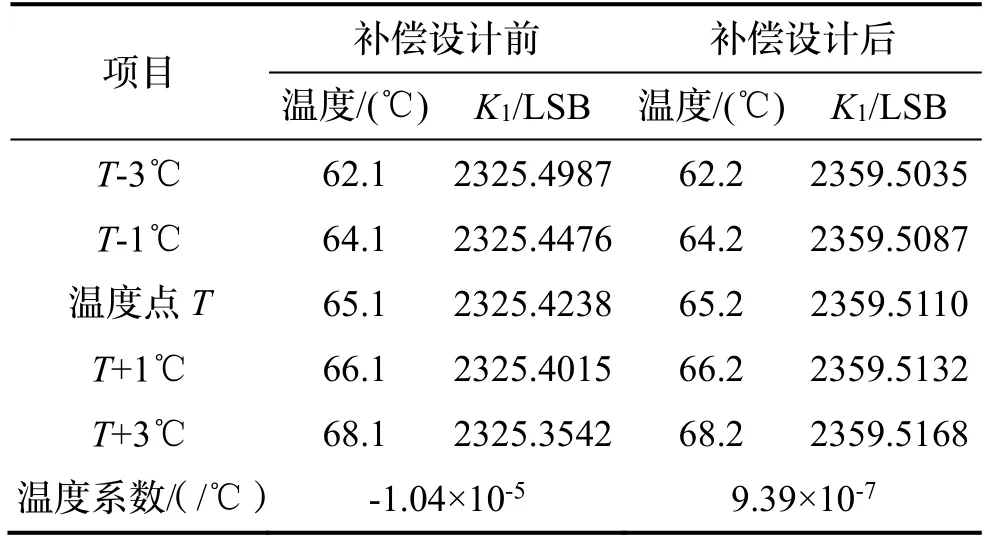
表1 温度系数测试结果Tab.1 Test result of the temperature coefficient

可以看出，补偿设计前仪表的温度系数为-1.04×10-5/℃，补偿设计后仪表的温度系数为9.39×10-7/℃，提升了一个数量级以上。以温控精度为0.03℃计算，则一次项的温度误差可减小至2.8×10-8，这对液浮陀螺加速度计的精度提升效果显著。

此外，由于仪表的实际结构参数与理论值存在一定偏差，且浮子的不同结构部位也存在一定的温度梯度，因此，补偿设计后的温度系数实测结果并非为零。

5 结论

为减小液浮陀螺加速度计内部温度变化对仪表性能的影响，本文分析了液浮陀螺加速度计一次项温度系数的作用机理和计算方法，提出了一种基于结构设计的温度系数补偿方法。在浮子结构上去除一定量的体积，使得浮油作用到浮子上的浮力随温度的变化，来补偿仪表摆性温度变化率与角动量温度变化率的不匹配量，进而降低一次项的温度系数。通过试验验证表明，采用结构设计补偿后，仪表的一次项温度系数由-1.04×10-5/℃降低至9.39×10-7/℃。在同等温控精度条件下，该方法可将温度系数降低一个数量级，这对液浮陀螺加速度计的精度提升具有一定的工程应用价值。

后续将在材料的实测线膨胀系数、仪表内部温度梯度等方面开展研究，进一步减小仪表实测的温度系数，提升该项技术的实际应用效果。