基于FDTD 的高深宽比沟槽结构低相干显微干涉信号仿真分析

赵雨晴，高志山，袁群，马剑秋，孙一峰，郭珍艳

（南京理工大学 电子工程与光电技术学院，南京 210094）

0 引言

随着制造与加工工艺的不断发展，高深宽比沟槽结构在半导体、传感及光学领域体现出优越的性能，被广泛应用于微光机电系统（Micro-Electro-Mechanical System，MEMS）、梳齿式加速度传感器等器件中。高深宽比沟槽结构的深度、线宽等形貌特征参数使得上述器件具有独特的光学、催化和动力学特性，满足了器件对高驱动力、低噪声、高灵敏度等性能的迫切要求，因此实现高深宽比沟槽结构形貌特征参数的精确检测对加工过程控制、器件质量评定具有重要意义。

非接触式的低相干垂直扫描干涉技术［1］以其检测成本低、效率高、稳定性好等优点被广泛应用于微结构的形貌特征参数检测中。该技术采用宽带光源，通过构建测试光路和参考光路，在系统垂直扫描过程中形成一组干涉条纹图像，干涉图像中每一个采样点对应的干涉信号包含一个高斯包络且包络峰值点对应的扫描位置为当前采样点的纵向高度，通过形貌复原算法［2］提取干涉信号包络并定位其峰值点对应的垂直扫描高度信息，可实现对被测结构形貌特征参数的精确检测。然而，高深宽比的结构特征会导致该技术检测得到的干涉信号异常，进而影响检测结果的准确性。JO T 等在使用Linnik 型干涉系统检测深度47.9 μm、直径4.27 μm 的硅通孔时发现，高深宽比的结构特征会遮挡测试臂入射光束，导致返回光能量弱于参考臂，从而降低干涉信号的对比度［3］。MONTGOMERY P C 等在检测深度75 μm、线宽2 μm 的微光机电系统时，发现在梳齿结构上边缘水平方向向空气延伸的位置附近，相干扫描会出现异常干涉条纹［4-5］，导致错误的形貌复原结果。

近年来，为了分析测量系统和被测结构特征参数对探测信号的调制规律，研究异常干涉信号的形成机理，进而改进形貌复原算法，提升形貌检测精度，越来越多的研究基于不同的理论仿真建立干涉信号模型，并将其与实验测量结果相比较验证所建模型的准确性。目前，基于衍射理论（如Kirchhoff 衍射理论、Richards-Wolf 衍射理论）的仿真建模［6-8］通常被应用于表面形貌存在微小起伏的结构。但由于衍射理论的有效性限制，该类方法无法完善描述高深宽比等复杂结构特征对探测光的多重散射作用。因此，一些研究采用更为严格的基于麦克斯韦方程组求解的数值仿真方法。TAVROV A 等采用严格耦合波分析（Rigorous Coupled Wave Analysis，RCWA）数值仿真得到了高深宽比沟槽结构表面调制光场，并结合构建的相干方程得到了与实验相近的仿真结果［9］，研究发现当光源偏振方向垂直于沟槽方向时，结构的遮挡以及复杂衍射效应所引起的干涉条纹异常现象最为明显。BISCHOFF J 等［10］分别基于有限元法（Finite Element Method，FEM）、严格耦合波分析和Kirchhoff 衍射理论仿真得到一维矩形光栅的干涉图及形貌复原结果，通过与实验测量结果相比较，指出相比基于衍射理论的仿真建模，即使数值仿真所设置仿真区域为二维，也能够和实验结果有较好的一致性。THOMAS 等［11-12］采用边界元法（Boundary Element Method，BEM）同样在二维仿真区域内得到了阶跃结构、V 型槽等表面调制光场，并得到了与实验测量结果相近的仿真干涉图及其频域分布。然而，严格耦合波分析通常仅适用于周期性结构，边界元法在面对同非线性项相对应的区域积分时求解困难，有限元法运算步骤复杂且通常用于求解单一频率的探测光场，此外对探测光与尺寸大于十倍光波长的结构相互作用中光场的传输过程计算耗时长且效率低。相比之下，时域有限差分法（Finite Difference Time Domain，FDTD）在离散的网格空间中数值求解麦克斯韦差分方程组，能够直接通过时域的递推精确模拟光场的传播过程，不仅适用于各种周期性及非周期性结构，并且对宽带探测光与高深宽比沟槽微结构的相互作用过程的计算效率较高。

本文采用FDTD 数值模拟光场的传输过程，首先计算得到入射会聚光经被测结构调制后的表面返回场，然后针对低相干垂直扫描干涉的测量过程，引入垂直扫描过程并建立理想的显微成像系统，同样采用FDTD 将所得到的一系列不同步进量下的调制光场传输至系统像面，最后结合所构建的相干方程叠加参考光场数据，获取被测结构的低相干显微干涉信号。分别仿真得到深宽比为5∶1、80∶3 的两种硅基沟槽微结构的表面调制光场，同时搭建与实验系统放大倍率一致的理想成像系统，将表面调制光场传输至系统像面，并进一步叠加参考光场数据，最后计算得到干涉信号。将仿真结果与实验室自研的Linnik 型低相干垂直扫描干涉系统对相同深宽比样品的检测信号进行比较，分析干涉信号的包络及幅频特征，证明采用所提方法建立的高深宽比沟槽微结构低相干显微干涉信号模型的准确性，并进一步分析受到结构复杂表面形貌调制的异常干涉信号对相应形貌复原算法准确性的影响。通过对所建干涉信号模型的提前分析，可为相应形貌复原算法的提出及改进奠定基础。

1 高深宽比沟槽结构的干涉信号特征

低相干垂直扫描干涉技术通常采用宽光谱光源，当发生干涉时，宽光谱干涉强度表示为

式中，z为测量臂的长度，z0为参考臂的长度，lc为光源的相干长度，λ0为宽光谱中心波长。由此可知，得到的理想干涉信号是一个周期为λ0/2 的高斯包络调制余弦函数，干涉信号高斯包络峰值对应的扫描位置为当前采样点的纵向高度。通常形貌复原算法在对干涉信号进行预处理之后，通过提取干涉信号包络，并定位包络峰值点所对应的垂直扫描高度信息，即可复原结构的形貌特征参数。预处理的目的在于提高干涉信号信噪比，保证复原形貌的准确性，常采用Gaussian 滤波、Winner 滤波等消除信号中的高频噪声，完全噪声辅助聚合经验模态分解［13］（Complete Ensemble Empirical Mode Decomposition with Adaptive Nosie，CEEMDAN）用于消除由于光照不均或样品表面反射率分布差异造成的光强信号低频漂移。包络提取算法主要包括希尔伯特变换法、小波变换法、傅立叶变换法等，其中Morlet 小波变换法［14］因计算精度高成为干涉信号包络提取的常用方法。

在测量高深宽比沟槽结构的实验过程中，发现不同采样点的干涉信号具有不同的特征［15］，如图1：被测结构上表面采样点的干涉信号对比度高且包含一组包络；结构下表面采样点，因结构对入射光的遮挡导致反射光能量低，使该位置干涉信号能量弱于上表面，由大范围扫描引起的光强漂移现象还会使干涉信号发生整体偏移。此外，高深宽比沟槽结构阶跃边缘复杂的衍射效应，会导致测量得到的干涉信号异常，包含两组甚至是多组包络，其中一组为包含结构下表面垂直扫描高度信息的有效信号包络，另一组为与结构上表面位置相对应的异常信号包络。采样点越靠近阶跃下边缘，下表面对应的有效信号包络幅值越小，甚至低于异常信号包络。

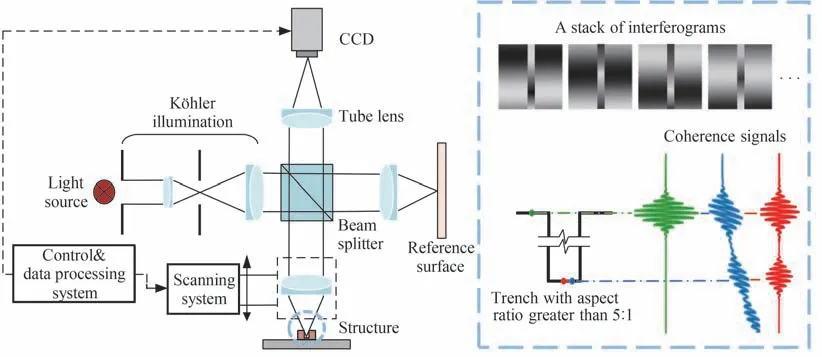
图1 高深宽比结构的低相干显微干涉信号特征Fig.1 Characteristics of low coherent micro-interference signal with high aspect ratio structure

2 仿真过程

仿真过程模拟低相干垂直扫描干涉系统测量高深宽比沟槽结构的过程，分为结构表面调制光场的仿真、显微成像过程的模拟、垂直扫描过程的模拟以及相干叠加获得干涉信号四部分。其中，前两部分都采用FDTD 数值模拟光场的传输过程。整个仿真过程在二维XOY面内完成，具体仿真流程如图2。

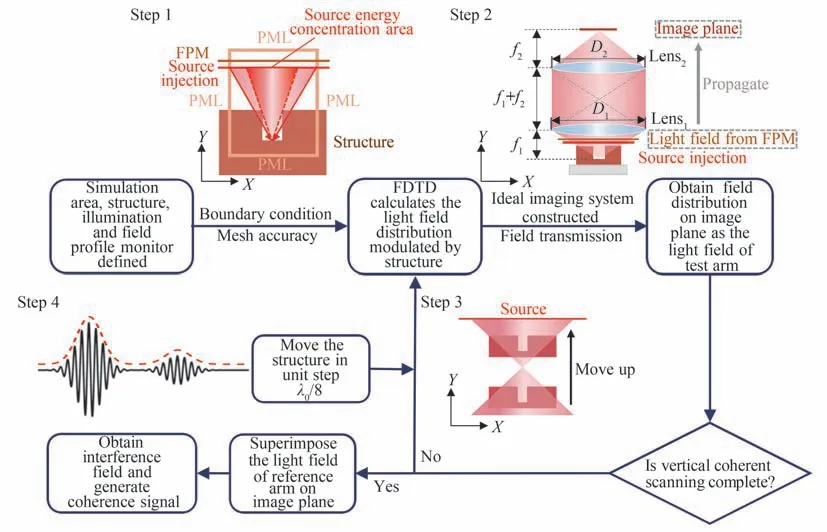
图2 仿真流程Fig.2 Simulation process

2.1 结构表面调制光场仿真

在直角坐标系XOY面内划定FDTD 仿真区域，在区域内定义被测结构的表面形貌、材料属性等特征参数，同时构建给定带宽∆λ及中心波长λ0的探测光源以及用于采集光场的场监视器（Field Profile Monitor，FPM），FDTD 模拟的二维仿真空间设置如图2 中步骤1 所示。为了避免不必要的谐振，被测结构基底及左右两侧应延伸至仿真区域以外，只以结构复杂表面形貌为中心划定二维仿真空间进行仿真。需要注意的是，由于场监视器真正能够采集光场数据的范围受到仿真区域宽度（沿X轴方向）的限制，为了能够采集到由被测结构表面反射的绝大部分光能量，同时保证仿真效率，将仿真空间的宽度设置为约探测光源注入面中光能量集中区域宽度的两倍。

此外，根据实验测量系统的显微成像光路，探测光源采用平行光束经口径大小为D1、焦距为f1的理想薄透镜Lens1会聚的球面波，如图2 中步骤2 所示，其在焦面位置处的光斑横向尺寸遵循瑞利判据，如图3。探测光主要沿Y轴方向传播至被测结构表面，结构表面形貌对探测光产生相位和振幅调制，场监视器紧贴在光源注入位置的后面，用于采集经结构表面调制后的反射光场数据。由于在远离被测结构复杂表面形貌的区域不存在明显的反射界面，因此仿真区域两个Y边界和两个X边界都采用理想匹配层吸收边界条件（Perfectly Matched Layer，PML）［16］，使入射到边界上的电磁波可以无反射地进入虚拟有耗媒质并逐渐衰减。

图3 焦面位置处的探测光场分布示意Fig.3 Distribution of detecting light field at focal plane

2.2 显微成像过程模拟

从2.1 节中场监视器直接获取的只是经被测结构表面调制后的、有限区间内的近场数据，但在实验测量中所采集到的一系列干涉图像，是经过显微物镜和管镜放大成像后的远场数据。为了模拟实验测量中的显微成像过程，定义两个口径分别为D1和D2、焦距分别为f1和f2的理想薄透镜Lens1、Lens2并将其共轭放置，构成显微成像系统，如图4。由于2.1 节中仿真采用的光源为会聚球面波，因此仿真模拟的理想成像系统实现的是物方单个采样点到系统像面单个像素点的放大成像。

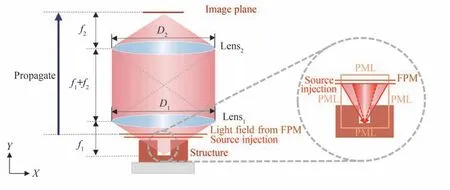
图4 仿真模拟成像过程Fig.4 Simulation of imaging process

成像过程采用FDTD 进行数值计算。首先，将经被测结构调制的近场数据分解为沿不同角度传播的平面波并传输到理想薄透镜Lens1，根据Lens1所给定的焦距f1和口径大小D1可计算得到Lens1的数值孔径NA1及相应的孔径角u1，由于数值孔径的限制，角度大于孔径角u1的平面波都会被舍弃，保留的光线通过Lens1会聚到其后焦面上；然后，同样对Lens1后焦面上的光场数据作分解并传输到理想薄透镜Lens2，计算得到Lens2的数值孔径NA2及孔径角u2，舍弃掉大于孔径角u2的分解平面波并将保留的光线会聚到理想成像系统的像面上。其中，数值孔径NA 与相应孔径角u的具体计算表达式为

式中，空间折射率（通常为空气折射率）约等于1。

整个光场传输过程还须借助等效原理［17-18］，应用有限区间内的光场数据，实现区间外光场的外推。等效原理简述如下：在散射体周围引入虚拟界面A，如图5（a），设A面外为真空。如果保持界面A处场E、H的切向分量不变，而令A面内的场为零，如图5（b），则根据唯一性定理，图5（a）和图5（b）两种情况在面A以外的场E、H有相同的分布。

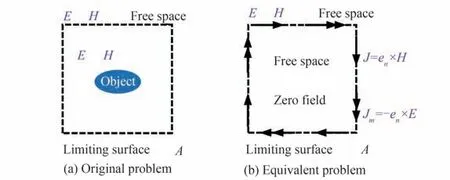
图5 等效原理示意Fig.5 Schematic of equivalent principle

在A面处存在等效面电流J与面磁流Jm（A面上E、H的切向分量），表示为

式中，en为面A的外法向。E与H的辐射场表示为

式中，A、F为矢量势函数，通过J、Jm以及 Green 函数可以确定矢量势函数，根据式（4）进一步推导出A面外的辐射场E、H。在二维情况下，Green 函数可近似为

式中，k=ker。设二维外推封闭面为l，推导可得二维情况下的矢量势函数为

同时定义电流矩tw和磁流矩tmw为

式中，w=x，y，z，表示电流矩和磁流矩分量的方向。利用上述公式，可推算得到二维直角坐标系下电场和磁场的纵向分量Ez、Hz，表示为

2.3 垂直扫描过程模拟

实验检测中，需要控制PZT 将干涉显微物镜分别调焦至结构上、下表面，并以上、下表面为中心进行±lc（光源相干长度）范围内的相干扫描。仿真建模时，首先应确定仿真区域中的待测采样点，接着模拟物镜的会聚光束对采样点进行沿光轴方向上的垂直扫描，最后得到采样点的干涉信号。仿真模拟的垂直扫描过程如图6（a），保持光源焦点位置不变并控制样品移动，扫描过程分三个步骤进行：

1）调整被测结构位置，使待测采样点与光源焦点重合，模拟实验中的对焦过程。

2）图中采样点设置在沟槽下表面中心位置，对图6（a）所示常规情况，以采样点为中心，仿真模拟±lc区间内的垂直扫描过程；对图6（b）所示结构深度大于lc的情况，以±0.5lc为区间完成下表面的垂直扫描后，以相同方式进行上表面扫描。

图6 仿真模拟垂直扫描过程Fig.6 Simulation of vertical scanning process

3）垂直扫描过程中设置步进量step，控制结构以由下向上进行移动，场监视器在扫描过程中同步记录结构表面的调制光场数据，至此完成扫描过程。

2.4 相干叠加获得干涉信号

将参考平面反射的光场数据和2.1 节与2.3 节在结构表面记录的垂直扫描调制光场数据，通过2.2 节中介绍的理想显微成像系统，采用FDTD 光场传输至系统像面，随后提取参考臂及测试臂的电场矢量E、H，根据式（9）进行矢量叠加，最终得到干涉光场数据，表示为

式中，电场矢量E、干涉光场I是随垂直扫描位置y变化的函数。

基于FDTD 数值计算显微成像过程时，设置的成像传输后的像方采样间隔远小于实际检测中CCD 像元尺寸l。为后续将仿真与实验结果相对比，以干涉光场强度最大值的位置为中心划定±l/2 的区域，对内部所有像方采样点的强度值求平均，将结果作为被测结构表面选定的待测采样点在当前扫描位置的干涉强度值。根据扫描顺序逐步拼接干涉强度值，得到采样点的初始干涉信号。最后采用CEEMDAN 算法进行干涉信号的预处理，消除大范围相干扫描过程中存在的光强漂移现象。

值得注意的是，仿真过程中采用2.2 节介绍的理想显微成像系统，期间并未考虑实际检测时系统衍射极限作用的影响。为使仿真结果更接近真实值，进一步考虑当前采样点邻域范围内干涉信号由于衍射作用产生的叠加效果：进行二维仿真时，首先以像元尺寸l对应的物方间隔为采样间隔设立当前采样点相邻的点为辅助采样点，接着以所阐述的仿真方法对辅助采样点进行干涉信号的计算，考虑如图7 所示系统点扩散函数幅值的衰减情况，则当前采样点受其相邻两个辅助采样点的影响最为明显，根据式（10）进行仿真干涉信号的强度叠加，表示为

图7 衰减因子与系统点扩散函数示意Fig.7 Schematic of attenuation factor and point spread function

式中，Ifinal0为当前采样点最终的干涉信号，I0为当前采样点预处理后的干涉信号，I1、I2为左右相邻辅助采样点的干涉信号，α为衰减因子，其大小可根据物方采样间隔d和系统点扩散函数求得［19］。

3 仿真与测量结果的比较与分析

为验证仿真方法的准确性并进一步分析高深宽比沟槽结构的异常干涉信号，分别仿真得到深宽比为5∶1、80∶3 的硅基单沟槽微结构下表面采样点的低相干显微干涉信号，并与实验室自研的Linnik 型低相干垂直扫描干涉系统测量相同深宽比沟槽微结构所得结果进行比较。实验系统光源采用带宽∆λ为100 nm、中心波长λ0为1 325 nm 的短相干近红外光（相干长度lc约为17.56 μm），PZT 带动测试臂在给定区间内以步进量step（165.625 nm，λ0/8）从下往上移动，实现垂直扫描，系统两臂显微物镜的放大倍率为20 倍（NA 为0.5），CCD 像元尺寸l为20 μm，两像素间隔对应物方采样间隔为1 μm。仿真过程模拟实验系统的测量过程，所设置的仿真参数与实验一致。

3.1 深宽比5∶1 沟槽微结构的干涉信号分析

仿真构建深度10 μm、线宽2 μm 的硅基沟槽微结构，待测采样点位于沟槽底部，如图8，采样点间隔与实验测量时的1 μm 物方采样间隔保持一致。根据第2 节所述的仿真过程，调整沟槽微结构使待测采样点与光源焦点位置重合，以此位置为中心，进行±17.56 μm（±lc）区间内的垂直扫描，仿真得到不同光源偏振方向下（垂直于沟槽方向的TEs光和平行于沟槽方向的TEp光）待测采样点的干涉信号，光源焦点位置所对应的垂直扫描步数为第107 步，如图9。

图8 深宽比5∶1 硅基沟槽微结构下表面采样点位置Fig.8 Location of tested sampling point of Si-based trench micro-structure with aspect ratio of 5∶1

图9 不同光源偏振方向下深宽比5∶1 的硅基沟槽微结构沟槽底部采样点的干涉信号仿真结果Fig.9 Simulated interference signals of Si-based trench micro-structure with aspect ratio of 5∶1 under different polarization directions

进一步采用实验系统测量深度10 μm、线宽2 μm 的硅基沟槽微结构并提取沟槽底部的干涉信号数据。以实验测量时的垂直扫描方向为中心旋转沟槽微结构，发现在不同角度下，所得到的结构沟槽底部的干涉信号特征相似，如图10 所示，这是由于实验采用的光源（SLD1325）为非偏振光的原因。

图10 深宽比5∶1 的硅基MEMS 沟槽微结构的实验测量结果（干涉信号为CEEMDAN 算法预处理之后的结果）Fig.10 Experimental results of Si-based MEMS trench micro-structure with aspect ratio of 5∶1（the interference signals are the result of CEEMDAN preprocessing）

进一步比较图9 及图10 仿真结果与实验测量结果，发现TEs光对应的仿真干涉信号与实验干涉信号具有较好的一致性。相比TEp光对应的仿真结果，由于TEs光的偏振方向垂直于沟槽方向，高深宽比沟槽结构特征所导致的遮挡效应和衍射效应明显，干涉信号不仅幅值很小并且包含多个异常信号包络，此时下表面位置对应的有效信号包络幅值甚至低于异常信号包络幅值。由此证明虽然实验采用非偏振光入射，但是TEs光的偏振方向对测量结果的影响远大于其它偏振方向。因此，在之后深宽比80∶3 硅基沟槽微结构的仿真中，将直接采用TEs偏振会聚光作为仿真光源。

3.2 深宽比80∶3 沟槽微结构的干涉信号分析

仿真构建深度80 μm、线宽3 μm 的硅基沟槽微结构，采用TEs偏振会聚光入射，得到被测结构下表面中心采样点Ps1和其相邻的阶跃下边缘采样点Ps2的干涉信号。为后续便于将仿真结果与实验结果对比，对所得到的干涉信号，以结构上、下表面对应的垂直扫描位置为中心，分别截取±50、±30 扫描范围内的干涉信号并重新拼接，结果如图11。

图11 拼接处理后的仿真干涉信号Fig.11 Simulated interference signals after splicing

进一步选取实验测量深度80 μm、线宽3 μm 的硅基MEMS 沟槽微结构得到的下表面沟槽中心采样点、阶跃下边缘采样点的干涉信号，实验测量结果如图12，图中展示的干涉信号已通过CEEMDAN 算法预处理。

图12 深宽比80∶3 硅基MEMS 沟槽微结构实验测量结果Fig.12 Experimental results of Si-based MEMS trench micro-structure with aspect ratio of 80∶3

以实验被测结构上、下表面所对应的垂直扫描位置为中心，同样分别截取±50、±30 扫描范围内的经过预处理后的干涉信号并拼接，结果如图13。

从图11 和图13 间的对比可以看出，由于仿真光源及仿真区域为二维形式，探测光会聚到结构表面后反射的光能量弱于实际检测时的光能量，因此仿真干涉信号的强度相比于实验信号会有所衰减，在比较过程中可将二者同时进行归一化处理，如图14。

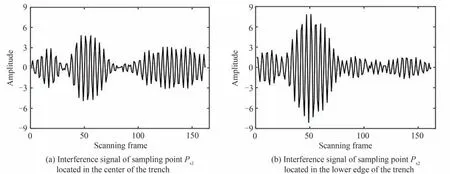
图13 拼接处理后的实验干涉信号Fig.13 Experimental interference signal after splicing

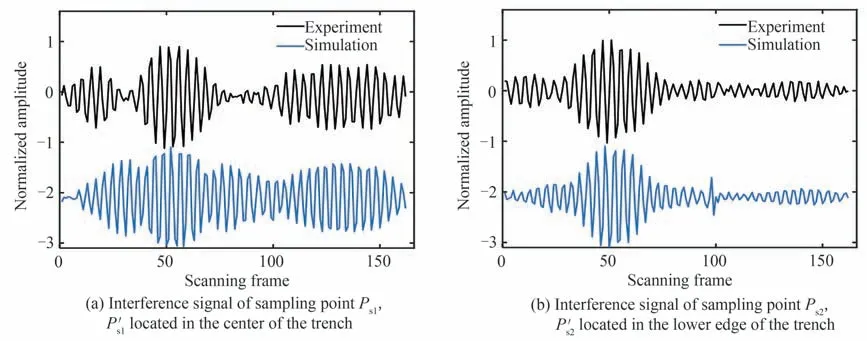
图14 归一化后的实验干涉信号与仿真干涉信号对比图Fig.14 Comparison diagram of normalized experimental interference signal and simulated interference signal

从对比结果中可以看出，受二维仿真形式、仿真建立结构与实验测量时样品结构间区别的影响，虽然仿真干涉信号相比实验干涉信号的形式存在细微差别，但二者的信号特征近乎相同，初步证明了仿真模型的准确性。接着采用Morlet 小波变换算法提取干涉信号包络，进一步比较信号的变化趋势，同时对干涉信号进行傅立叶变换提取频域信息并进行幅频结果的比较，其结果分别如图15 和图16。

图15 实验干涉信号与仿真干涉信号包络对比Fig.15 Envelope comparison of experimental interference signal and simulated interference signal

从实验干涉信号与仿真干涉信号的包络结果可以看出，对于深宽比80∶3 的高深宽比沟槽结构而言，下表面的干涉信号中均包含两个包络，其中左侧异常包络及右侧有效包络的扫描位置分别对应结构的上表面及下表面。当采样点逐渐接近阶跃边缘时，从图15（a）至图15（b）的信号变化中可以看出右侧包络的幅值显著衰减，这是由于高深宽比沟槽结构遮挡作用时边缘位置处采样点的信号能量及信噪比降低的缘故。从干涉信号包络的实验检测及仿真结果间的对比可以看出，包络都具有双峰性特征且包络的幅值、包络峰值点对应的扫描位置都近乎相同，从而证明了本文提出的仿真方法可以成功地对实验结果进行模拟。此外，从信号解调的角度出发，干涉信号中存在的双包络现象将使采用重心法的相干峰位置定位算法失效，且将影响多项式拟合法对零光程差位置的求解。此外，由于左侧异常包络幅值大于右侧有效包络的影响，采用Morlet 小波变换等算法提取干涉信号的包络后，针对双包络信号无法简单地定位相干峰位置。

从实验干涉信号与仿真干涉信号的幅频结果可以看出，对深宽比80∶3 的高深宽比沟槽结构进行检测时，系统中心波长对应波数附近的幅频结果出现异常，表现为形式不对称且不具备单峰性的特点。这是由干涉信号双包络的特征所引起，且当采样点接近阶跃边缘时，从图16（a）至图16（b）幅频有所衰减。从干涉信号幅频的仿真结果可以看出，其表现出的双峰性特征与实验结果相同，证明了本文所提仿真模型的有效性。此外，从信号解调的角度出发，幅频结果的异常会导致基于频域信息求解的空间频域算法失效，影响零光程差位置的求解。

图16 实验干涉信号与仿真干涉信号的频域分布对比Fig.16 Frequency distribution comparison of experimental interference signal and simulated interference signal

通过比较深宽比80∶3 沟槽微结构的仿真与实验测量结果，分析干涉信号的包络及幅频特征，证明了所提仿真方法可对实验干涉信号进行准确模拟。此外，由于异常干涉信号会影响相应形貌复原算法的准确性，可通过提前分析仿真干涉信号特征，为后续信号解调算法的选取及有效包络的确定提供指导。

4 结论

本文提出了基于FDTD 的低相干显微干涉信号仿真方法。通过划定仿真区域并设置仿真基本参数建立二维仿真空间，然后划定垂直扫描范围，以给定步进量从下往上移动被测结构模拟系统的垂直扫描过程，同时采用FDTD 计算得到一系列步进量下的结构表面调制光场数据。在此基础上，构建理想成像系统模拟实验的显微成像过程，同样采用FDTD 将表面调制光场传输至系统像面，最后叠加参考光场数据获得所需的干涉信号。分别仿真得到深宽比5∶1、80∶3 的硅基沟槽微结构下表面采样点的干涉信号，并与实验系统测量相同深宽比沟槽微结构得到的干涉信号数据进行对比，通过对干涉信号包络及幅频特征的比较，证明所提仿真方法的准确性，并进一步分析异常干涉信号对相应形貌复原算法准确性的影响。随着高深宽比沟槽结构在半导体、传感器及微纳光学领域愈发广泛的应用，越来越多的研究基于低相干垂直扫描干涉技术进行数值仿真并建立干涉信号模型，通过与实验测量结果的比较验证仿真所建模型的准确性，进而研究分析测量系统和被测结构参数对干涉信号的调制机理，为改进形貌复原算法、提升检测精度奠定基础。本文所提出的基于FDTD 的数值仿真方法为实验测量高深宽比沟槽结构提供了有效的理论干涉信号模型，可以在实验检测前对干涉信号进行先验性计算，提前分析干涉信号的特征，并为信号解调算法的选取及有效包络的确定提供指导，为形貌复原算法的改进奠定基础。且该仿真方法同样适用于理想平面、光栅、V 型槽等各种周期性或非周期性结构。在未来的研究工作中，可将仿真模型从二维扩展到三维，与此同时优化算法效率，使其具备更为广阔的应用前景。