基于非局部自相似性的双相机压缩光谱图像重建算法

朱骏捷，赵巨峰，田海军，崔光茫，石振

（1 杭州电子科技大学 碳中和新能源研究院，杭州 310018）

（2 杭州电子科技大学 电子信息学院，杭州 310018）

0 引言

高光谱成像相比常用的RGB（红、绿、蓝）三色成像，能够拍摄更多的光谱通道，获得更多被测目标的特征和细节，从而广泛应用于遥感［1］、医学成像［2］、环境监测［3］等领域。高质量、高精度的光谱成像与重建方法是本领域追求的目标之一。

高空间、光谱、时间分辨率的光谱成像技术是未来的发展方向。为了快速获取目标光谱信息，BRADY D J 等提出了编码孔径快照式光谱成像系统（Coded Aperture Snapshot Spectral Imager，CASSI）［4-6］。这是基于压缩感知理论［7］发展起来的一种快照式的光谱成像技术，它对三维光谱数据进行稀疏低维采样，在二维探测器上获得混叠的光谱信息，然后通过计算重建出三维光谱数据，只需要一次曝光就能获得目标的光谱信息，具有获取光谱视频的能力。由于从二维采样中重建三维光谱数据是一个欠定的问题，重建误差不可避免，如何减小重建的误差是该成像方式的关键问题之一。

为了提高重建质量和精度，研究者们在重建框架中引入了不同的正则化方法。使用全变差正则化［8-9］作为约束的算法是一种常用的重建算法，它假设图像具有分段光滑性，但是这种正则化方法会使图像过度平滑，损失一些细节。针对采样数量的限制，KITTLE D等［10］通过拍摄多帧编码图像来进行重建，即通过增加采样数量提升重建质量，但同时也破坏了CASSI获取光谱视频的能力。WANG Lizhi等［11-12］在原来的CASSI基础上增加一路相机进行互补采样，在提升重建质量的同时保持了快照特性。TAN Jin等［13］将小波变换作为稀疏基，提出了一种基于3D维纳滤波的近似消息传递法，但是这种预先定义的正交基不能很好地表示自然场景，因此限制了重建质量。一些研究者通过研究高光谱图像的内在特性，例如非局部性自相似性［14-15］、低秩特性［14，16］等，提出了不同的重建模型，但通常重建时间过长或者重建质量有限。近几年，深度学习被应用于CASSI重建，研究者们设计了不同的网络结构用来重建编码图像。MIAO Xin等［17］联合注意力机制与U-net设计了λ-net来实现端到端的高光谱图像重建。文献［18］中提出了一种具有空间光谱自注意力机制的模块来利用空间光谱相关性。然而，基于学习的方法通常需要数据来训练模型，并且重建效果容易受到训练数据的影响，限制了模型的泛化能力。

非局部自相似性在图像重建、去噪、超分辨率［19-21］中有广泛的应用。在过去的一些方法中，由于只有退化的图像而没有更多的信息，相似性估计等操作都是通过重建的中间结果进行的，并且在重建过程中需要不断进行估计，对于尺寸较大的光谱图像非常费时。为了获得高质量的光谱图像重建，本文提出了一种基于非局部自相似性与双相机系统的重建算法，用双相机系统来获取目标信息，然后用RGB 观测获取的额外信息来辅助重建。首先，利用高光谱图像存在的空间局部、非局部相似性以及谱间相关性，提出一种压缩光谱图像的重建模型，将恢复问题转化为变分优化模型；然后，采用RGB 观测来辅助字典学习，并对目标的光谱图像存在的非局部相似性进行估计；最后，采用一种交替优化的方案来完成高光谱图像的重建。

1 双相机系统模型

双相机系统如图1 所示，入射光进入系统后被平均分成两份，一份进入CASSI 系统被灰度相机捕获，一份被RGB 相机捕获。定义目标场景为f0(i，j，λ)∈RM×N×Ω，其中i，j表示空间坐标，λ表示光谱坐标，M，N表示空间尺寸，Ω表示通道数量。CASSI 分支(i，j)的压缩测量可以表示为

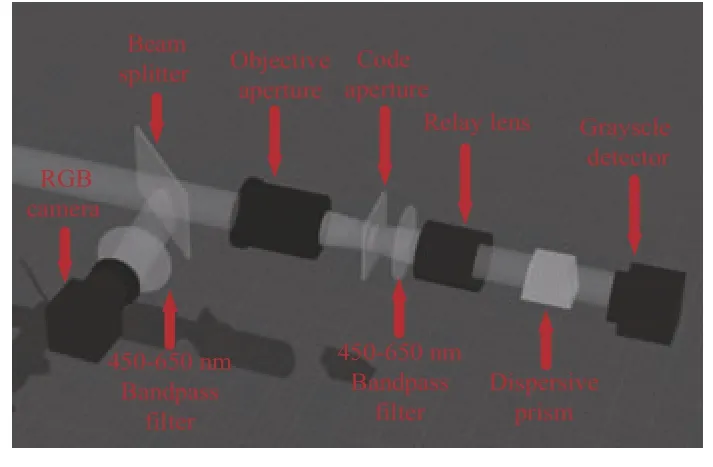
图1 双相机系统Fig.1 The system of dual camera

式中，ωc(λ)表示灰度相机的响应曲线，T(i，j)表示编码模板，φ(λ)表示棱镜的色散函数。CASSI 分支的采样可以写成线性矩阵形式，即

式中，Hc∈RN(M+Ω-1)×MNΩ，表示感知矩阵，yc∈RN(M+Ω-1)和Vc∈RN(M+Ω-1)分别表示观测图像和噪声的向量形式，F∈RMNΩ表示目标高光谱图像向量。对于RGB 相机分支，3 个通道的观测图像分别是目标高光谱图像有效光谱范围内的积分，RGB 分支的测量可以表示为

相应的线性矩阵形式为

式中，Ho∈R3MN×MNΩ表示RGB 相机的前向响应矩阵，Vo∈R3MN是观测噪声，则

式中，yr，yg，yb分别为3 个通道的观测图像的向量表示。联合两个分支的测量，整个双相机系统的前向模型可以表示为

其中

2 高光谱图像重建算法

高光谱图像是一个高度稀疏的信号，在空间和谱间都存在着丰富的信息冗余。具体表现为：光谱维度上，自然场景的光谱可以由6～8 个主成分来表示［22］，并且同一场景中存在很多光谱曲线相似的区域。空间维度上，同一张图上可以找到很多相似结构的图像块。在充分考虑这些先验信息的基础上，构建了一种三维非局部稀疏表示模型来提升重建性能。

首先，使用RGB 观测进行辅助字典学习。将初始化的高光谱图像F按步长为1 分割成空间尺寸为b×b×Ω的跨全光谱波段的重叠立方体块。然后，将RGB 相机分支获得的RGB 图像的3个通道图像也分别按步长为1 分割成尺寸为b×b的二维图像块。假设分别是RGB 三通道位于坐标(i，j)的图像块的向量表示，定义

利用K 均值聚类对不同坐标的Xi，j进行分类，分成K个簇，然后以该聚类结果为指导将高光谱图像对应的立方体块进行相同的分类。定义Mk∈Rn×lk，表示第k个簇的立方体块向量组成的矩阵。其中n=b×b×Ω表示立方体块向量的长度，lk表示第k个簇的立方体块个数。对每个簇的立方体块矩阵使用主成分分析降维，获取该簇的特征作为这个簇的字典，定义第k个簇的字典为Φk∈Rn×n。

定义向量xi，j∈Rn表示从高光谱图像F中取出的一个三维光谱块向量表示，处于坐标(i，j)的位置，即

式中，Ri，j∈Rn×MNΩ是一个块提取矩阵，从F中以步长为s提取三维光谱块xi，j。根据聚类结果找到xi，j所属的簇，利用获取的字典Φk给当前簇中的块xi，j进行稀疏编码，通过一个簇中共有的特征对当前簇中的其它块进行约束。对于给定的字典Φk，在充分考虑高光谱图像的谱间相似性、空间局部相似性与非局部相似性的基础上，构建重建模型为

式中，xi，j，q表示在图像块xi，j为中心的一个窗口Ωi，j内第q个相似块，ωi，j，q是相应的加权系数。

由于除了退化的图像外没有更多的信息，xi，j的相似 块xi，j，q通常是根据重建的中间结果来估计［19-21］，但是对于尺寸比较大的三维光谱块非常费时，并且在重建过程中需要不断进行相似块的估计，进一步增加了时间花费。另一方面，由于重建误差的存在，从中间结果来估计相似块不一定准确。针对这一问题，用双相机系统的RGB 观测获取的额外信息来进行相似块的估计，由于RGB 图像每一个通道是目标高光谱图像一小段光谱范围的积分，如果两个图像块在RGB 三个通道的距离都非常近，那么目标高光谱图像的两个光谱块之间距离也非常近。

以Dm，i的大小来估计目标高光谱图像的两个图像块之间的相似度。因此，可以定义

通过Dm，i的大小来为每个三维图像块xi，j找到与它距离最近的J个块。

在实验过程中，正则化参数η的大小对重建结果影响明显，如果η比较大，能比较好地抑制稀疏编码噪声，但同时也会抑制一些有用的成分。当η比较小时，会导致重建时受稀疏编码噪声影响较大，出现收敛速度过慢或者重建结果变差的问题。加权lp范数能提升稀疏性，得到更好的结果［23-24］，因此设置了自适应参数

式中，l表示向量αi，j中第l个元素，c是一个预先设置的常数，ε是一个比较小的常数。因此，将重建模型扩展为

式中，ηi，j是一个对角矩阵，ηi，j，l是对角线上第l个元素的值。

为了求解式（15），将优化问题分解成两个子优化问题，然后交替优化来求解。在(t+1)次迭代中，对于固定的F，稀疏编码系数α的优化为

用迭代收缩算法［25］来求解式（16），经过计算，α中的每个元素可以由式（17）得到。

式中，l是一个向量中的第l个元素，αijl表示向量αi，j的第l个元素。

对于固定的α、F可以通过式（19）的子问题进行更新。

这是一个二次优化问题，可以求出闭合解为

由于矩阵H尺寸很大，无法直接求解，用共轭梯度下降法来求近似解。通过式（17）和式（20）交替更新α和F，然后每T次迭代更新一次字典Φk，直到收敛，就能获得重建的目标光谱图像。

3 实验结果

3.1 实验细节

为了证明所提方法的有效性，用CAVE 数据集［26］进行测试。CAVE 数据集包含了31 幅400～700 nm 波段的光谱图像，分辨率为10 nm。实验中，测试图片裁剪出大小256×256×31 的中心区域作为参考图像，并归一化到［0，1］。实验中光谱块尺寸大小为4×4×31，采样步长s为2×2，簇的个数K为50，对于每个图像块都在25×25 的窗口中找到距离最近的15 个块，迭代次数为400，编码模板服从p=0.5 的伯努利分布。实验中的对比方法有两种，分别是基于秩最小化的算法（DeSCI）［14，27］，基于自监督神经网络的算法（PnP-DIP）［28-29］。本文方法与DeSCI 的实验是在CPU 为i7-10750H，内存为16 G 的笔记本电脑上使用MATLAB 2016a 完成，PnP-DIP 实验是在GPU 1080Ti的服务器上完成。

为了评估重建图像的质量，用峰值信噪比（Peak Signal to Noise Ratio，PSNR）、光谱角制图（Sepctral Angle Mapping，SAM）［30］、结构相似度（Structural Similarity，SSIM）［31］来衡量重建质量。其中PSNR 与SSIM 衡量重建的空间质量，值越大表示空间信息重建质量越好；SAM 衡量重建的光谱曲线准确度，值越小表示重建的曲线与真实曲线越相似。

3.2 仿真数据测试

3.2.1 重建质量与精度

在CAVE 数据集上的实验结果如表1 所示，每个图像的最佳结果以粗体突出显示。可以看出本文方法在PSNR、SSIM、SAM 上都有显著的提高，在空间质量和光谱精度上优于其它方法。观察PSNR 的变化，DeSCI 的平均PSNR 是25.80 dB，PnP-DIP 是30.45 dB，本文方法是42.68 dB，相比DeSCI 平均提升了16.88 dB，约65%，比PnP-DIP 平均提升12.23 dB，约40%。从SSIM 和SAM 中可以看出，本文方法重建的光谱图像在空间结构和光谱曲线的精度上也是最高的。

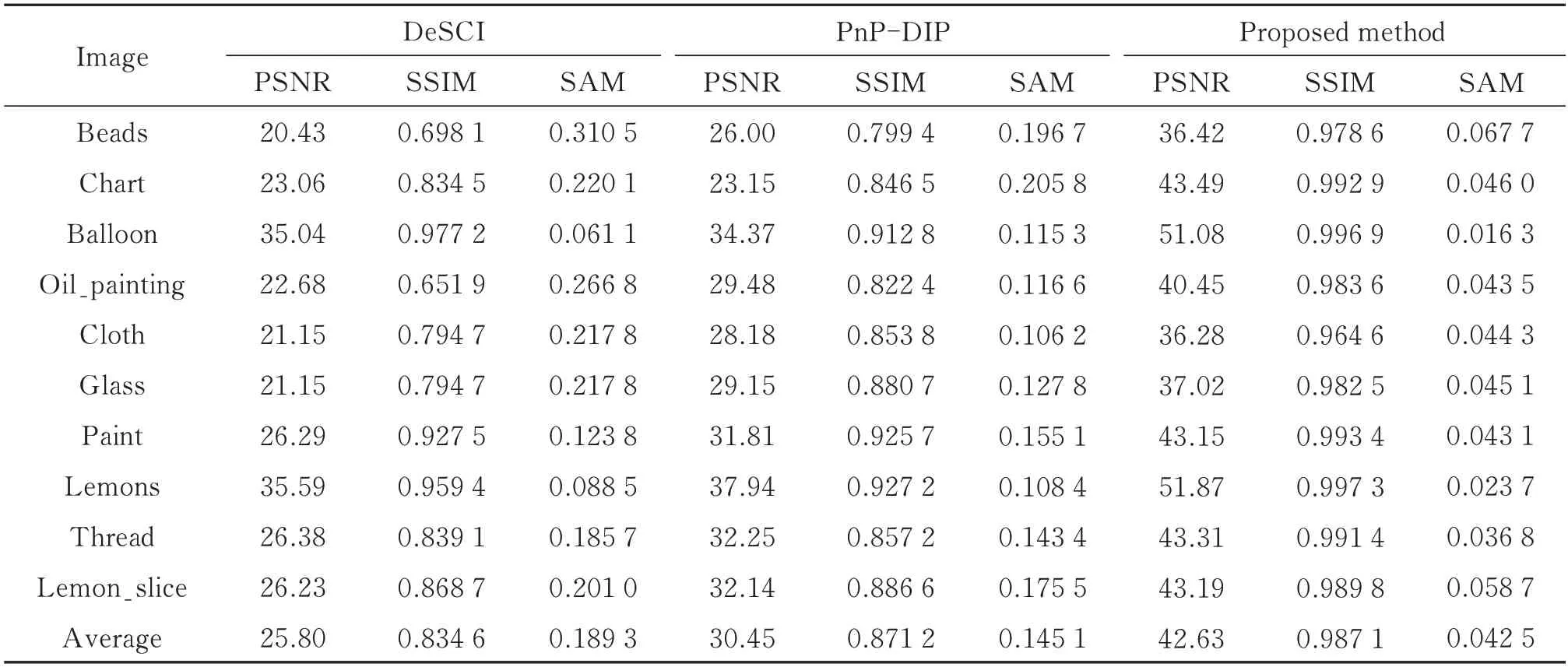
表1 CAVE 数据集重建结果对比Table 1 Comparison of reconstruction results of CAVE dataset

3.2.2 重建视觉效果对比

为了进一步比较重建质量，图2 给出了不同方法在670 nm 波段的重建图像，对重建图像的视觉质量进行比较。可以看出本文方法在视觉效果上好于其他方法。DeSCI 利用了高光谱图像的组稀疏性，通过加权核范数最小化的方式进行重建，这可能会导致重建的图像比较平滑。PnP-DIP 通过从观测图像中学习先验，并在重建过程中不断优化网络，获得了更好的重建结果，但仍然存在明显的伪影。从两个场景的重建图片和局部放大图片中，可以看出本文方法对于一些细小的纹理仍然能比较好的地重建出来，而其他方法在细节上都存在不同程度的损失。本文所提方法在视觉效果上也明显好于其他三种方法，不管在定量还是定性的比较上都获得了更好的效果。

图2 chart 和glass 在670 nm 的重建结果对比。第一行为chart 场景，第二行为glass 场景Fig.2 Comparison of reconstruction results of chart and glass at 670 nm.The first line is the chart scene，the second line is the glass scene

3.2.3 光谱维度重建误差分析

为了直观比较光谱域的重建误差，取重建的高光谱图像chart 中两点进行比较，图3 显示了A、B两点在不同方法下各个波段的绝对误差。在所有结果中，本文方法在所有波段都有最小的重建误差，且较为稳定，其他方法在不同波段的重建误差波动较大。表2 显示了chart 场景重建结果所有点光谱曲线平均绝对误差的均值，可以看出本文方法在整个场景光谱曲线的重建上也有明显更小的误差。

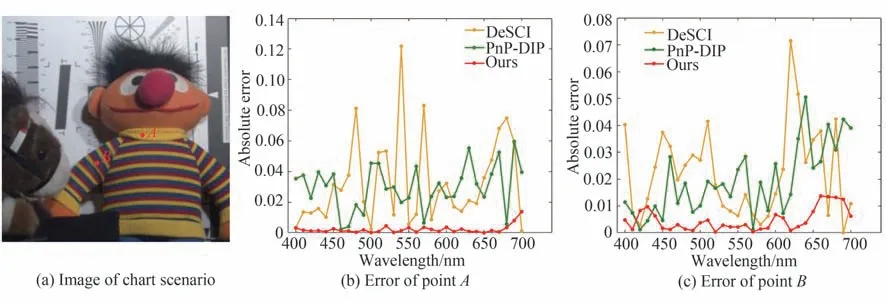
图3 光谱曲线重建误差对比Fig.3 Comparison of spectral curve reconstruction errors

表2 平均绝对误差对比Table 2 Comparison of mean absolute error

3.2.4 兼顾质量的重建效率分析

首先对比了本文方法与DeSCI，PnP-DIP 的计算时间。针对chart 场景，三种方法重建时间如表3 所示。DeSCI 需要进行相似块的匹配需要花费较多的时间，但是由于算法较快的收敛速度所以所需的时间比本文方法要少。PnP-DIP 从观测图像中学习先验，需要花费较长的时间，但是重建结果要好于DeSCI。本文方法重建模型比较复杂，达到收敛所需的迭代次数比较多，所以花费时间较多，但是仍比PnP-DIP 要快，并且重建质量在三种方法中是最高的。

表3 chart 场景中不同方法重建时间对比Table 3 Comparison of reconstruction time of different methods in chart scenarios

事实上，本文方法在兼顾质量的重建效率提升方面也做了改进工作，主要体现在针对双相机体系，提出的RGB 辅助字典学习与非局部相似性估计有效降低了重建时间。为了对比提出的RGB 辅助字典学习与非局部相似性估计的策略和过去常用的中间结果字典学习与相似性估计［23-25］策略的重建结果与重建效率的区别，用本文提出的重建模型在不同场景下测试，同时在chart 场景测试了两种方法的重建时间。重建的PSNR 对比结果如图4 所示，重建效率对比如表4 所示。从图中可以看出两种方法重建结果非常接近，但是在重建时间上RGB 观测辅助重建的方法节约了约47%。

表4 chart 场景中RGB 辅助字典学习与相似性估计方法以及中间结果字典学习相似性估计方法的重建时间对比Table 4 Comparison of reconstruction time between RGB assisted dictionary learning and similarity estimation method and intermediate result dictionary learning similarity estimation method in the chart scene

图4 RGB 辅助字典学习与相似性估计方法以及中间结果字典学习与相似性估计方法的结果对比Fig.4 Comparison between RGB assisted dictionary learning and similarity estimation method and intermediate result dictionary learning similarity estimation method

3.3 实拍数据测试

搭建了如图5 所示的系统来进一步测试所提方法。该系统使用的物镜为azure-0918M3M（焦距9 mm），中继镜为Edmund C45762，灰度相机为PointGray FL2-20S4M，RGB 相机为PointGray FL2-20S4C，两个相机的像素尺寸都为4.4 μm×4.4 μm。编码模板是一个300×300 的随机二值矩阵，每个最小单元尺寸为8.8 μm×8.8 μm。棱镜为定制的双阿米西棱镜，该棱镜使得550 nm 的光能笔直穿过棱镜。

图5 双相机成像系统Fig.5 Dual camera imaging system

系统拍摄的图像如图6，重建的结果如图7 所示。展示了543 nm、606 nm、650 nm 三个波段的重建结果，并使用滤光片拍摄图像作为参考。可以看出本文方法重建的图像视觉效果要更好，保留了更多的细节，与参考图像相似度最高。

图6 两个分支的观测图像Fig.6 Observation images of two branches

图7 实拍数据重建结果Fig.7 The reconstruction results of real data

3.4 参数的讨论

重建过程中，图像块大小b、采样步长s和参数c对重建结果的影响比较明显，结果如图8 所示。图像块太小时会破坏图像块的结构特征导致结果变差；图像块太大会使得恢复信号的难度增大，并且增加重建的耗时。采样步长比较小时会放大重建的误差使得结果变差，并且重建时间也会变长；而步长太大时块效应会变得明显。将图像块大小设置为4×4×31，采样步长s设置为2。

参数c的影响如图8（c）所示，可以看出c比较大时迭代前期PSNR 提升会比较快，收敛更快，c比较小时收敛比较慢，但最后PSNR 值更高，重建的空间误差更小。为了平衡这两个因素选择c=0.001 5。

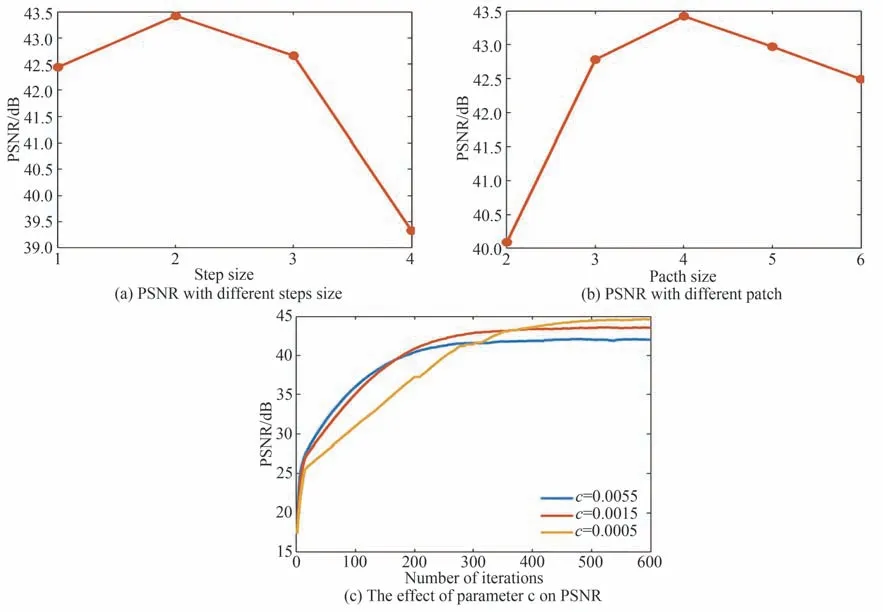
图8 不同参数对重建结果的影响Fig.8 Influence of different parameters on reconstruction results

4 结论

本文提出了一种基于非局部自相似性与双相机的高光谱图像重建方法。利用高光谱图像的内在特性，包括空间自相似性、光谱相关性和联合相关性，构建了模型来提高重建性能，并使用RGB 观测来辅助字典学习和相似块估计，最后通过迭代重建出高光谱图像。实验表明本文提出的重建模型能大幅提升光谱图像的空间和光谱维度的重建质量，并且使用RGB 观测辅助重建有效减少重建时间。虽然本文方法能获得高的重建质量，且在RGB 观测的辅助下降低了重建时间，但是重建时间仍然比较长，如何进一步减少重建时间是未来的研究方向之一。