城市输水系统应对水锤的韧性评价及其应用研究

宗 琦,许仕荣

(湖南大学土木工程学院,中国 长沙 410082)

《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》首次提出建设”韧性城市”。城市供水安全作为韧性城市体系的重要组成部分而备受重视[1]。在城市输水系统中,水锤是影响其安全运行的重要因素。IWA(国际水协)在2010年提出:大型调水工程的安全问题70%～80%是由水锤引起的。另外,水锤是导致供水管网老化和损坏的主要原因,并最终产生爆管,这不仅会导致水资源的浪费,还会严重影响城市的生活、生产和公共安全[2]。因此,研究输水系统应对水锤的韧性对于提高供水安全稳定性及推动“韧性城市”的高质量建设具有重要意义。

早在20世纪70年代,Fiering等在评估生态系统应对扰动的能力时就引入了韧性的概念:韧性(Resiliene )指的是系统吸收、恢复或抵抗外界扰动的能力[3];Aldunce等提出了基于韧性理论的应对致灾风险的管理策略[4];Bruneau等提出了一个定义韧性的概念框架,指出了韧性系统的四个重要特性[5]。Hashimoto等将韧性概念引入供水系统中,对供水系统的可靠性、韧性和脆弱性进行了区分[6];Todini等提出了应用于环状给水管网优化设计中的韧性指标[7];刘海星基于韧性理论建立了给水管网的3个评价指标[8]。而目前关于输水系统韧性的研究报道较少,基于此,本文以韧性理论为基础,提出输水系统应对水锤韧性的概念,并建立相应的量化指标,评价并优化输水系统应对水锤的韧性,以期为输水系统的水锤综合防护设计提供参考。

1 输水系统应对水锤的韧性及其指标的建立

输水系统应对水锤的韧性是指:输水系统在发生水锤时,仍能保持正常输水功能的能力。

1.1 韧性指标的数学表达

Farahmandfar等提出了用于评估供水系统应对地震的韧性指标[9]。仿此,本文提出输水系统应对水锤的韧性指标R:

(1)

式中:PFavg为输水系统管道在水锤作用下的平均失效概率。N为包括不同管径输水管道及连通管道在内的管道总个数。

在发生水锤时,管道上每一点的压力是不同的,故每一点失效概率也是不同的,为此定义系统平均失效概率如下:

(2)

式中:PFavg为管道的平均失效概率,L为管道长度,Pf是管道的失效概率函数,失效概率曲线上每一个点代表着管道上对应位置在水锤作用下的失效概率。

由式(2)可知,欲求PFavg,Pf的求解是关键。考虑到管道失效的不确定性,本文基于随机概率理论,对输水系统管道建立强度—应力功能函数,利用蒙特卡洛随机模拟法Monte Carlo Simulation(MCS),对管道失效概率进行计算。

1.2 失效概率Pf的求解

关于管道的失效机理,目前普遍被接受的理论是管道“结构抗力”的减小和“荷载效应”的增加导致了埋地管道的失效[10]。所谓“结构抗力”,指的是管道自身的管材属性,如钢材料的屈服强度,所具有的抵抗荷载的能力;所谓“荷载效应”指的是埋地管道在服役期间受到的直接或间接荷载,如土压力、内水压力、地震破坏及温度变化引起的应力等,作用在管道上的主要荷载如图1所示。本文从管道的“结构抗力”和“荷载效应”入手,构建强度—应力失效功能函数,利用蒙特卡洛方法进行失效概率的求解。

图1 管道作用荷载示意图

1.2.1 功能函数的建立 对于输水管道而言,其承受的荷载为土压力和内水压力,表现为环向拉伸应力和环向弯曲应力,此外还有泊松效应及温度变化导致的纵向拉伸应力。输水管道多采用金属管材,将管材的屈服强度作为结构抗力,利用Von·Mises失效理论建立功能函数如下:

(3)

式中:φ为焊缝系数,η是应力折算系数,一般取0.9;σs为管材屈服强度,σθ和σx分别是管道受到的环向应力和纵向应力。

(1)环向应力。管段的环向应力主要由内水压力在管壁界面上引起环向拉力以及土压引起的弯矩M产生:

(4)

式中:σθ为环向应力(Pa);PC代表内水压力(Pa),可通过水力瞬态过程模拟得到;D是管道的公称直径(mm);δ为管道壁厚(mm);ΔX是管道的横向变形量(mm),EP为管道材料弹性模量(N/mm2);Kb和Kz则代表着与沟槽基床角度有关的系数[11]。

对于式中ΔX的计算,在Watkins等提出的计算方法中没有考虑管道内压对横向变形的影响[12],显然偏于保守,参考日本相关规范[13],则考虑管道内水压力的变形量计算公式为

(5)

式中:W为土压力荷载;I为管道截面的惯性矩;E′为土体侧向弹性模量;rm为管壁中心半径;K为常数,仅与管底支承角有关。

目前,沟埋式回填管的土压力计算方法多以马斯顿在1913年提出的松散体极限平衡法作为基础,综合考虑GB50332中土压力的相关规定[14],给出土压力W的计算公式:

W=CdγsB。

(6)

其中,Cd—土压系数,Cd=[1-E-2Kμ′(H/B)]/2Kμ′,B为管顶沟槽宽度,γs则表示土壤容重,μ′为土壤特性系数,与土壤性质有关。

(2)纵向应力。纵向应力主要考虑温度效应和泊松效应,计算公式如下:

(7)

式中,μ为管道材料的泊松比;α为管道材料的线膨胀系数;ΔT指的是运行期管内的水温与安装温度之间的差值。

1.2.2 蒙特卡洛方法及其matlab实现 蒙特卡洛(Monte-Carlo, MC)方法根据人为构造的概率模型,依照该模型进行大量统计试验,使得某些统计参量正好是待求问题的解[15]。

利用蒙特卡洛方法求解失效概率的计算公式如下:

(8)

笔者利用自编的matlab程序实现蒙特卡洛算法求解失效概率的过程,算法程序框图如图2,其中所涉及的随机变量分布在下一节中详述。

图2 算法程序框图

1.2.3 随机变量的分布特征 王长新和张静等的研究给出了一些随机变量等所服从的分布,但对管段所受土压力的随机性没有阐述[16]。土压力的计算中涉及到的随机变量为土壤容重γs,土壤容重与土壤的成土过程及土壤属性有关,认为其服从γsmin—γsmax为99.74%置信区间的正态分布[17]。

内水压力是本文研究的重点,当发生水锤后,每个点的瞬时最大和最小压力可以分别连接成为一条压力包络线,故管道的内水压力以水力瞬态模拟后得到的压力值作为其均值,服从变异系数为0.05的对数正态分布。

对于其他随机变量,如管材屈服强度及焊缝系数等,根据误差理论及中心极限定理,认为其均值为设计值,标准差为均值的5%,服从对数正态分布[18]。

表1 随机变量的概率分布与统计特征

2 泵站加压输水系统应对停泵水锤的韧性计算实例

2.1 输水系统概况

南方某市原水输水系统如图3所示:设计水量为2 000 m3·h-1,输水管为两条DN500螺旋钢管,长度约4.5 km,在K1+050处用DN500钢管连通;泵站取水水面高程88.60 m,泵站地面高程90.60 m,蓄水池水面高程为276.50 m;泵站共安装同型号的水泵4台,三用一备,泵转速为n=2 900 r·min-1,水泵转动惯量为J=1.875 kg·m2;泵后缓闭止回阀的关阀动作为快关时间为10 s,快关阀门开度为0.3,总关阀时间为30 s。管道安装温度为30 ℃,运行期管内水温一般为14～20 ℃。

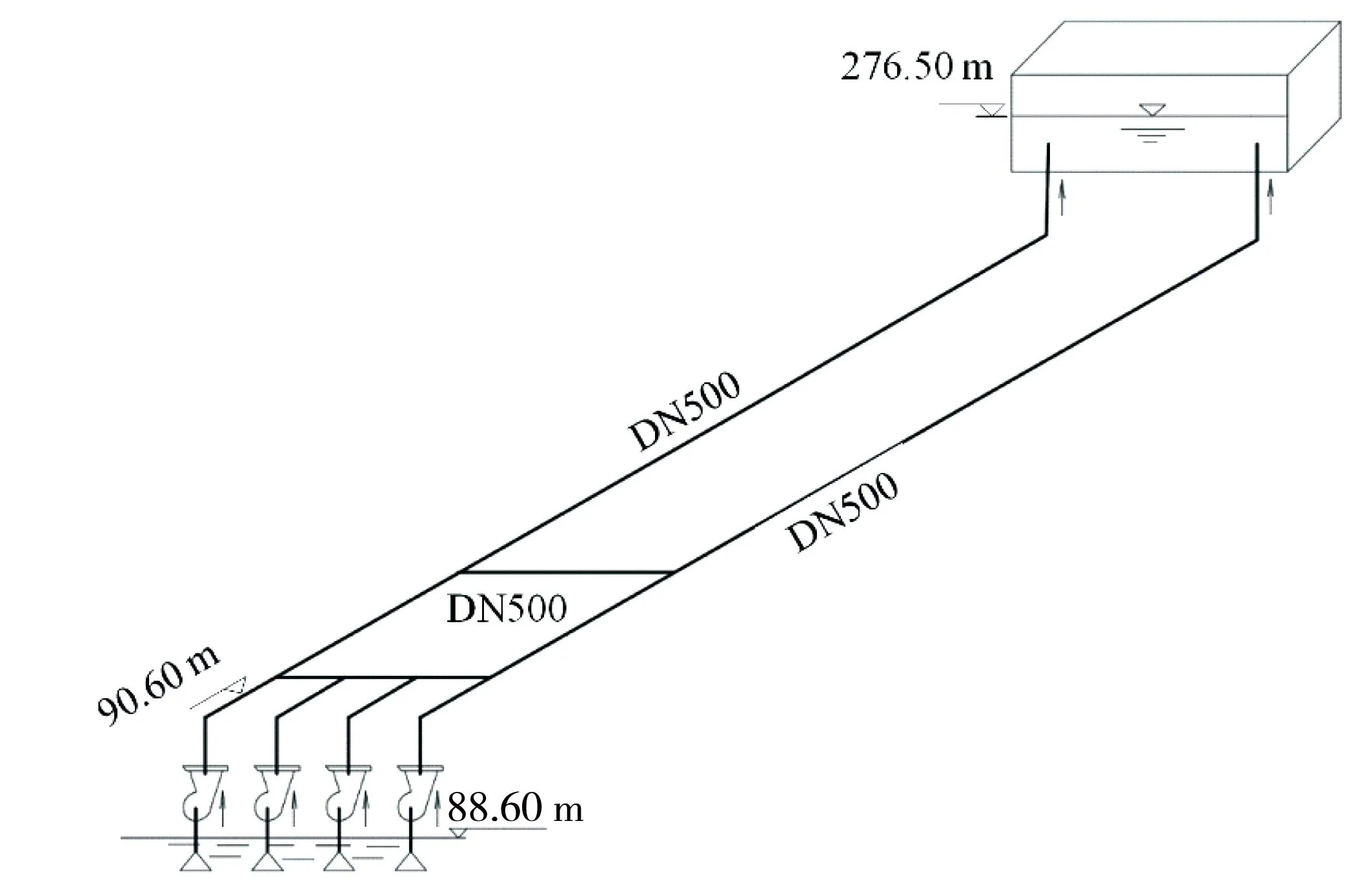
图3 输水系统示意图

2.2 水力瞬态过程的模拟

考虑三台水泵同时断电停泵这一最不利工况,利用美国Bently公司开发的Hammer V8i对其瞬态过程进行仿真分析,得到各计算管段的压力变化值。

未设置空气阀,输水系统发生停泵水锤时的压力包络线图如图4所示。

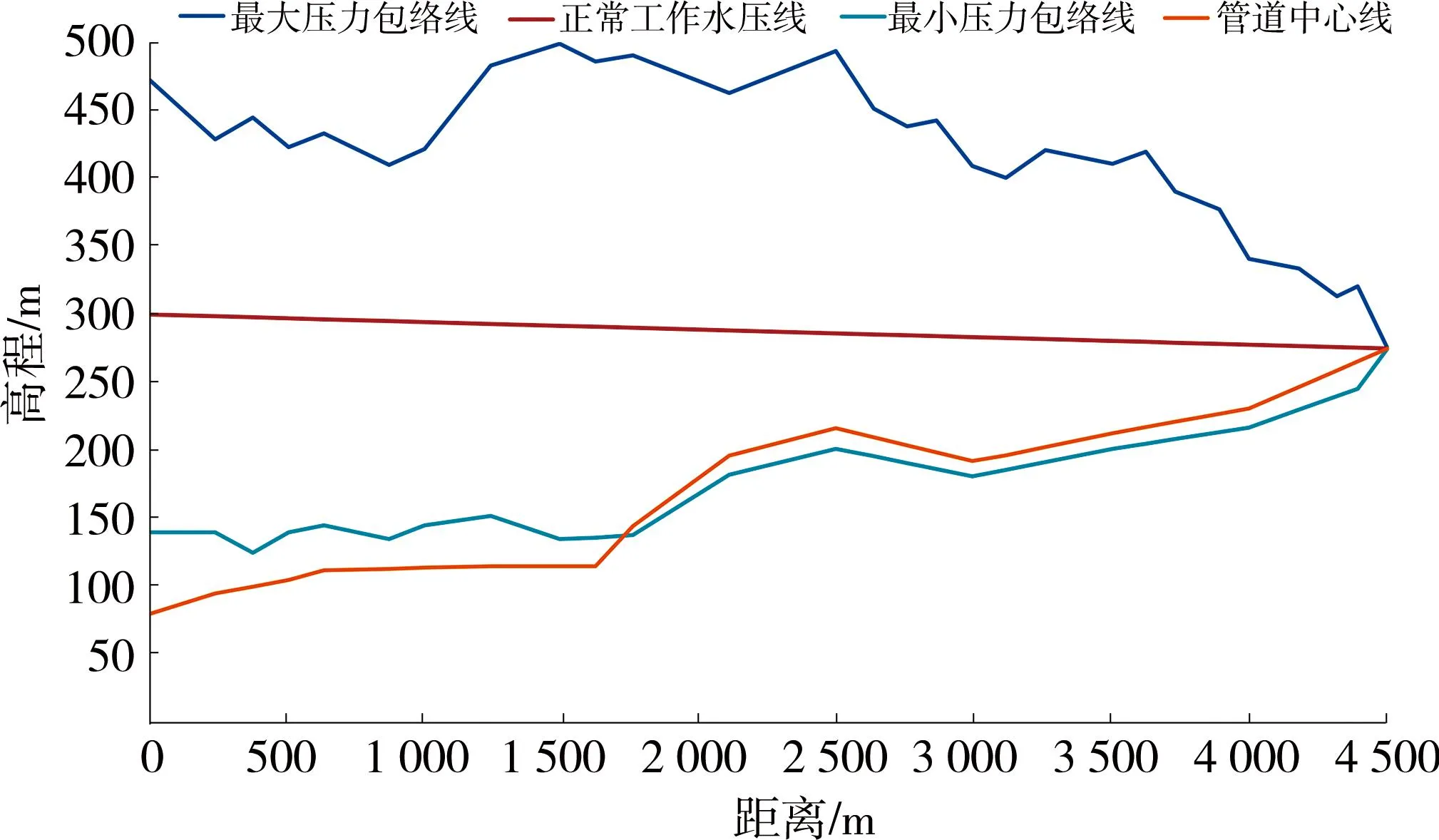
图4 未设置空气阀的管道压力包络线图

从图4可以看出,发生停泵水锤后,管道内压力可达正常工作压力的1.5倍甚至更高, K1+750后,出现了负压,且达到了-10 m,会出现汽化现象[19],必须采取相应的防护措施。

2.3 韧性指标值的计算

利用MATLAB分别计算管道失效概率,得到输水管沿管长方向的失效概率曲线Pf如图5所示。连通管上最高瞬时压力为297 m,其失效概率PFavg为0.321。

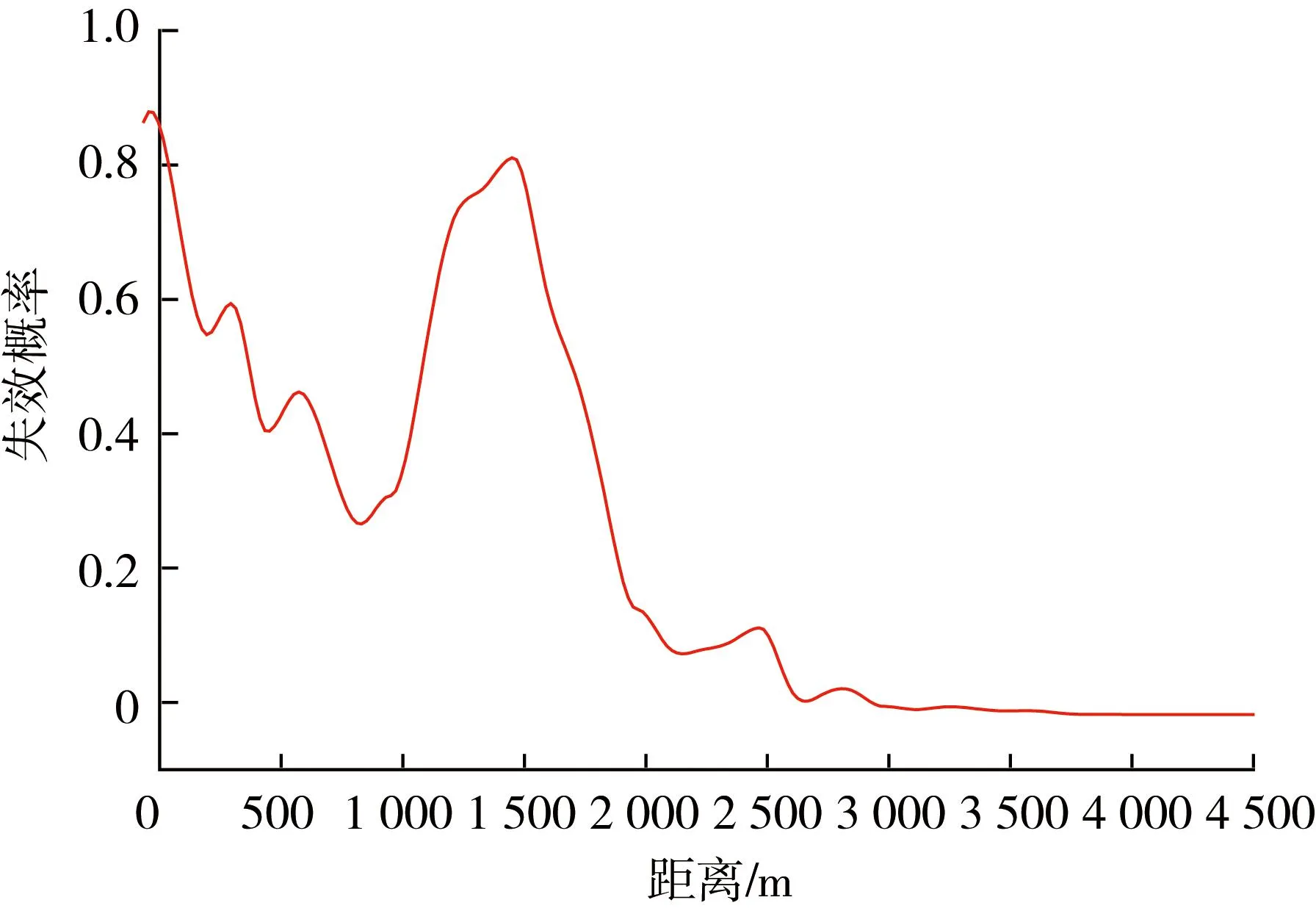
图5 管道失效概率曲线

根据得到的失效概率曲线,结合式(2),求出其平均失效概率为0.744。代入式(1),得到该系统韧性值为0.603。周晓帆等人[20]在研究中提出的将管道按照不同的失效概率划分为不同可靠程度,按此思路,将泵站加压输水系统应对水锤韧性评估标准列出,如表2所示:

表2 泵站加压输水系统应对水锤韧性评估标准表

由表2可得,在没有设置空气阀时,该输水系统如果发生停泵水锤,管道内升压较大,管道失效概率大,系统韧性较差。

3 空气阀参数优化

空气阀结构简单、安装方便、成本低且不受安装条件约束,是一种有效的水锤防护方案。两阶段空气阀解决了排气过快而导致的压力波动的问题,防护效果更佳[18]。在实际工程中,输水管路上空气阀的布置通常需要根据实际工程的运行条件及地形特点来确定。按照《室外给水设计标准》中要求[21],选择K1+010,K1+750,K2+473,K3+409和K4+000共5处设置空气阀,空气阀的具体位置如图6所示。

图6 空气阀位置设置示意图

3.1 空气阀参数正交试验设计

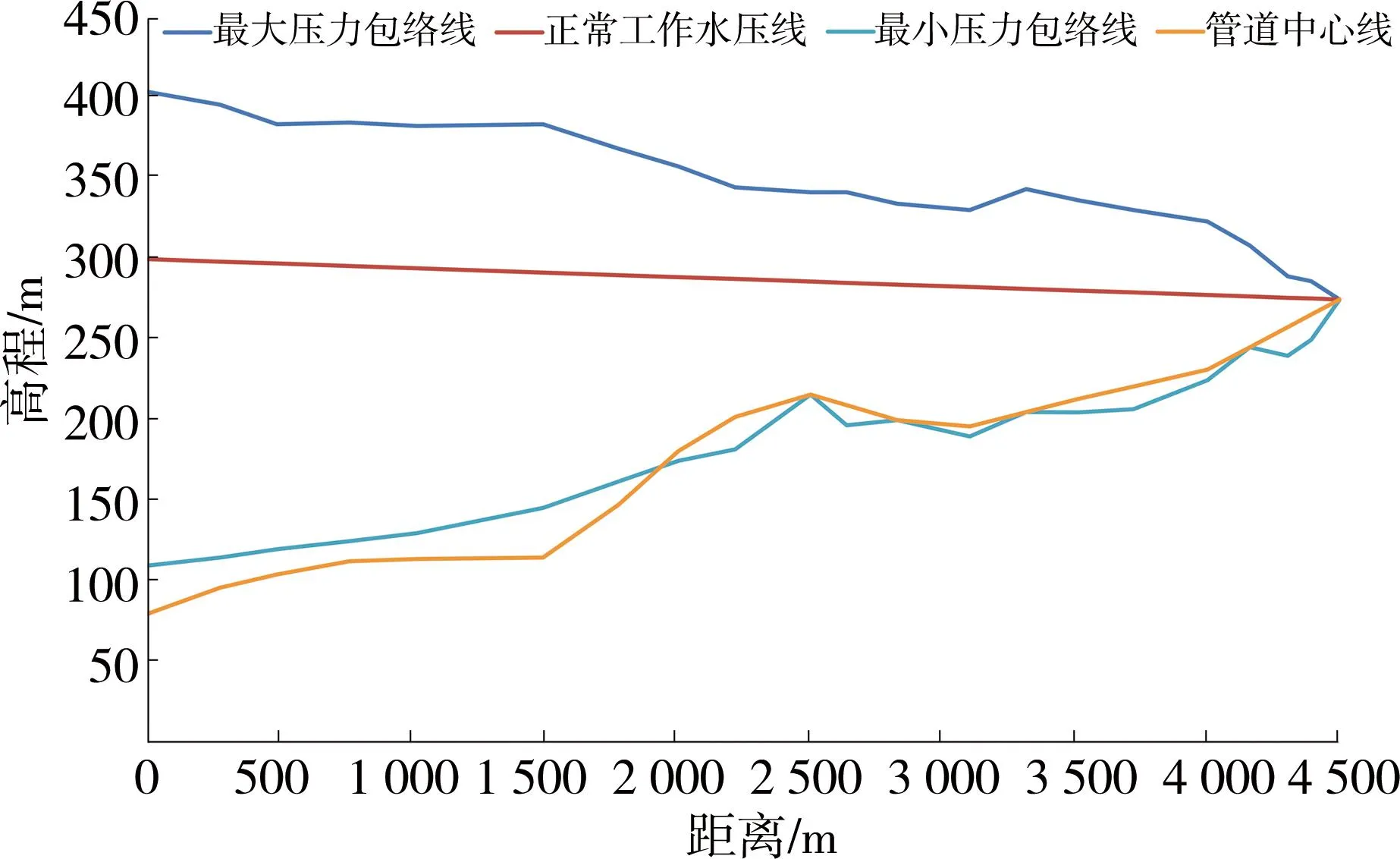
选取空气阀口径、进气系数、排气系数、大小排气口面积比、切换出流孔口的临界压力比等5个特性参数设计5因素4水平正交实验[22],以输水系统应对水锤的韧性指标为评价标准优化空气阀的参数设置。对于空气阀的口径,工程实践中一般取其输水管道直径的1/8～1/5,据此,本研究选取50,80,100和150 mm共4种口径;进气系数和排气系数均选取0.1,0.3,0.6和0.94个水平;孔口面积一般为0.2左右,本研究选择0.15,0.20,0.25和0.30共4个水平;两阶段关闭空气阀将空气以亚声速流出时的排气过程分为两个阶段,当1

表3 L16(45)正交验因素水平表

常见的空气阀尺寸[23]见表4。

表4 空气阀基础尺寸参考表

3.2 正交试验结果与讨论

按照式(1)和(2)的计算方法分别对16组试验的韧性值进行计算,得到的结果如表5所示,其计算结果可用如图7所示的管道压力包络线图来表示。

图7 空气阀参数优化后的管道压力包络线图

由表3.3的正交试验结果,可以直观看出不同的空气阀参数会对泵站加压输水系统韧性产生较大影响,其中试验11所对应的韧性指标值在16组试验中最高,为0.923,此时空气阀口径为100 mm、进气系数为0.6、排气系数为0.1、孔口面积比为0.2、临界压力比为1.10。

尽管空气阀参数不同,但试验6所得韧性指标值为0.920,与试验11结果相差很小,这说明空气阀各参数对系统应对水锤的韧性的影响是交互的。

由试验13～试验16的4组试验结果可以看出,当空气阀的口径超出输水管道直径的1/5时,会造成韧性指标值的骤降,这也说明空气阀孔径并非越大越好,在具体工程中应根据瞬态模拟结果合理选择。

从空气阀口径为80 mm和100 mm的8组试验中可以看出,在空气阀口径确定后,较小的排气系数有利于提高系统韧性水平,但进气系数过大,韧性水平会有所降低。这是因为分散或溶解状态的气体能大幅度降低水体弹性模量,从而降低水锤波速,抑制水锤升压,提高韧性,同时大气囊也可以吸纳水锤。但进气系数过大,导致管道内存气过多,一方面气囊的快速窜动会引起压力升高,另一方面气囊附近没有出口,密闭气囊就会产生较高的压力波。而排气系数过大时,如果发生停泵,在管道的“膝部”和“驼峰”位置发生断流,此时断流再弥合的过程中就会产生巨大的升压,较小的排气系数对再弥合的过程起到缓冲作用,减少升压。

参考表2所列评价标准并根据表3的结果可以看出,本案例的输水系统在合理地设置空气阀后,系统的韧性指标值提高至无防护措施的1.52倍,系统韧性等级由“较差”提升至“中等”。欲再提高系统韧性等级,须辅以其它防护措施。

4 结论

(1)提出了输水系统应对水锤的韧性这一概念,建立的系统韧性评价指标可以量化输水系统应对水锤的能力的评估。

(2)空气阀的各参数对输水系统应对水锤的韧性的影响是交互的,合理的参数设置可提高韧性,具体工程中应根据瞬态模拟结果合理选择。本研究中输水系统适宜的空气阀参数为:口径取100 mm、进气系数取0.6、排气系数取0.1、孔口面积比取0.2、临界压力比取1.10。

(3)对于输水系统来说,单一的水锤防护措施不一定能将系统韧性提至“较好”水平,此时应采取多措施并用的综合防护方案。