基于建筑碳排放与室内舒适度双目标优化方法的研究

朱泓宇,肖 敏*,张嘉敏

(长沙理工大学 a.建筑学院,b.电气与信息工程学院,中国 长沙 410114)

近年来,建筑业对人类社会资源消耗、环境保护和气候变化等多个方面的影响日益显著。《中国建筑能耗研究报告2020》指出,中国约46.5%的总能耗和51.6%的碳排放由建筑物产生[1]。为在2060年前实现“碳中和”目标,减少建筑物碳排放量成为一项必要且艰巨的任务。

在能源严重短缺的背景下,对建筑围护结构热工参数进行优化设计变得至关重要,这不仅有助于减少建筑碳排放,还能提高建筑运行阶段的热舒适性。在建筑性能优化研究领域,建筑模拟软件EnergyPlus和TRNSYS等被广泛应用于不同气候条件下高精度的建筑性能模拟。同时,Matlab和GenOpt也被广泛应用于建筑设计优化研究,通过探索大参数空间,实现建筑参数的优化[2]。Tavakolan等[3]将Matlab作为优化引擎,并将EnergyPlus作为动态能源模拟器,探索3种情景下的最小一次能源消耗和贴现投资回收期。Short等[4]通过监测典型楼层的室内气温和能耗,对中国现有高层建筑进行调查,并在EnergyPlus中进行模拟,提出了可行的节能低碳策略。因此,本文将EnergyPlus的建筑能耗模拟能力与Matlab的优化计算能力进行耦合,来探索评估建筑碳排放与室内热舒适性的最优条件。

近年来,深度学习作为一种灵活准确的数据驱动方法,在建筑性能预测领域愈加受到关注。神经网络作为一种能够开发高精度代理模型的数据驱动工具,已广泛应用于建筑性能研究。Wei等[5]结合盲系统识别和前馈神经网络来预测办公楼的占用水平和能耗。Rahman等[6]提出了一种递归神经网络模型,能够在一周多的时间内以1 h的分辨率间隔预测商业和住宅建筑的能耗。因此,本文通过Matlab神经网络工具箱生成BPNN,将其作为预测模型,构建拟合函数。

在致力于减少建筑碳排放的同时,还需提升建筑室内热舒适度。但由于两者优化目标相互冲突,且只存在一组非支配解决方案,因此优化算法的选择显得尤为重要。Zhai等[7]提出了一种NSGA-Ⅱ和EnergyPlus相结合的多目标优化方法,通过优化窗户参数,以确定平衡热舒适性。Naderi等[8]综合EnergyPlus和jEPlus对智能遮阳百叶窗进行优化,并通过NSGA-Ⅱ算法实现多目标优化。目前,建筑性能优化主要采用NSGA-Ⅱ算法,其他算法在该领域应用较少。因此,本文旨在综合比较MOEA/E,NSGA-Ⅱ和NSGA-Ⅲ三种优化算法,以确定最佳优化方法和建筑参数。

1 研究方法

为对建筑数据模型实施优化,在Matlab平台实现了神经网络的学习与训练,并耦合了开源的MOEA/E,NSGA-Ⅱ和NSGA-Ⅲ三种优化算法的程序。研究流程如图1所示。

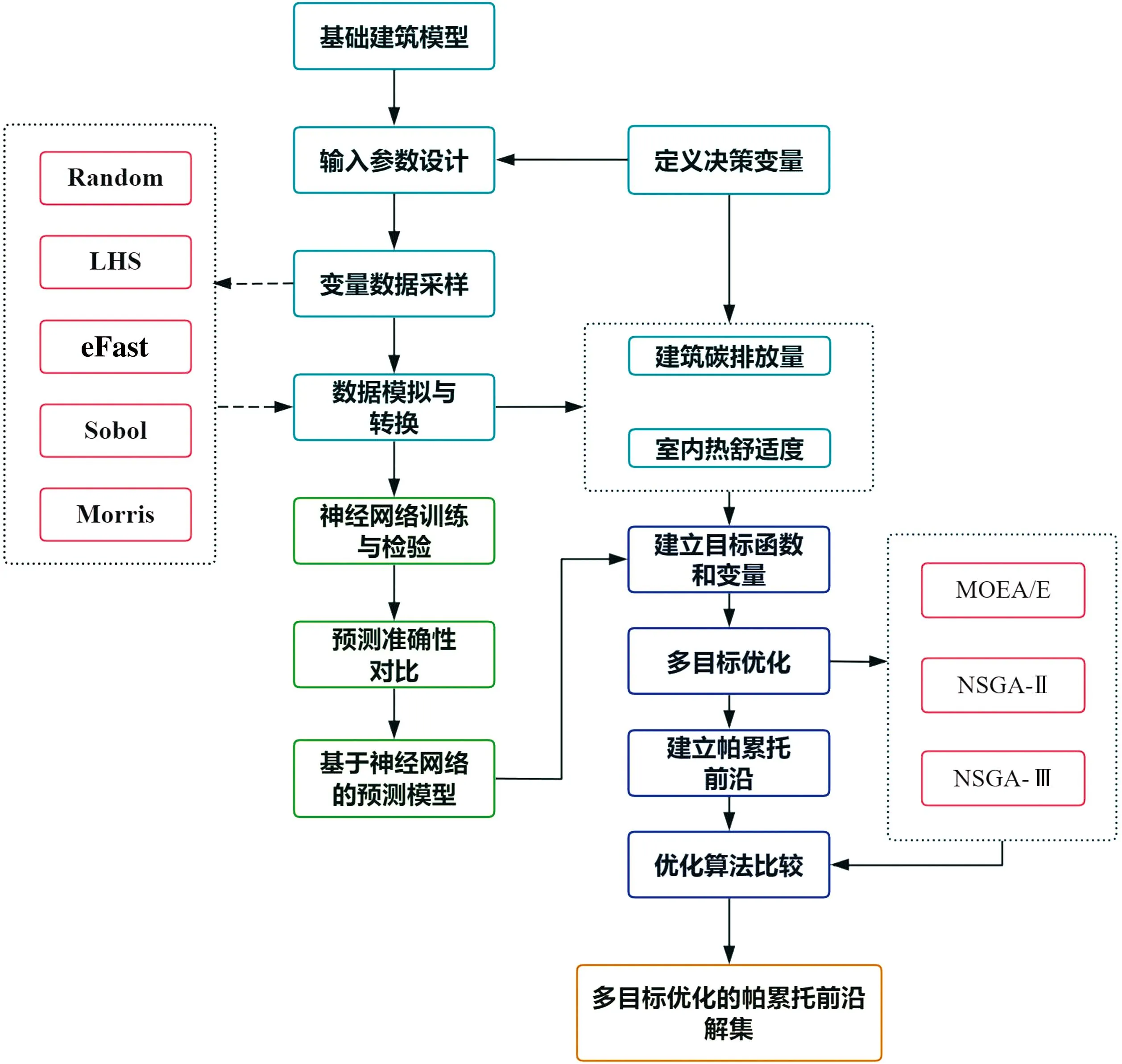
图1 研究流程

首先,建立基础模型,使用SketchUp创建多目标优化的建筑3D模型,并导入OpenStudio中定义热区,保存为idf.文件。再利用EnergyPlus打开idf.文件,创建案例基础建筑模型。将建筑年碳排放量和建筑室内热不舒适时间定义为优化目标,并从建筑围护结构和能源控制系统等方面选取对建筑碳排放和室内热舒适度影响较大的28个参数作为输入数据。

在确定输入参数后,为保证BPNN预测的准确性,选用多种采样方法,并比较采样空间的范围。分别运用eFast,Sobol,LHS,Morris及Random五种采样方法对输入参数进行采样,同时使用SimLab完成对数据集的采集[9]。采集的样本将进行合理分类,70%的样本用于神经网络学习,30%的样本用于验证神经网络的准确性。

为缩短仿真时间,通过功能强大的参数化工具JEPlus软件[10]将SimLab中抽取的样本自动设置为EnergyPlus的输入文件,集成启动EnergyPlus进行仿真,并收集用户所需的仿真结果。然后,将收集的仿真结果导入Matlab中,用于BPNN的训练与验证,验证可用后的BPNN能够对两个目标函数进行快速准确的预测。将验证后的BPNN作为多目标优化问题的目标函数,分别在MatLab中运行MOEA/E,NSGA-Ⅱ和NSGA-Ⅲ优化算法。最后,保存Pareto最优解即为算法的最终结果。

1.1 研究案例模型

由于高层公寓建筑内部热区复杂,因此在EnergyPlus中建立三层高的简化建筑模型(图1)。一楼为建筑底层,考虑地表与地表空气、对流换热与辐射换热的影响;二楼代表建筑中间层,受室外气候条件的影响最小;三楼为建筑顶层,考虑屋顶太阳辐射热的影响。

建筑基本信息见表1。空调、设备、照明、人员活动时间等信息均基于实际调查数据。通过对16户居民的实际居住情况进行调研,并使用K-means算法进行聚类,分别得到工作日与休息日两种情况下的人员在室内率曲线[11],如图2所示。

表1 建筑基本信息

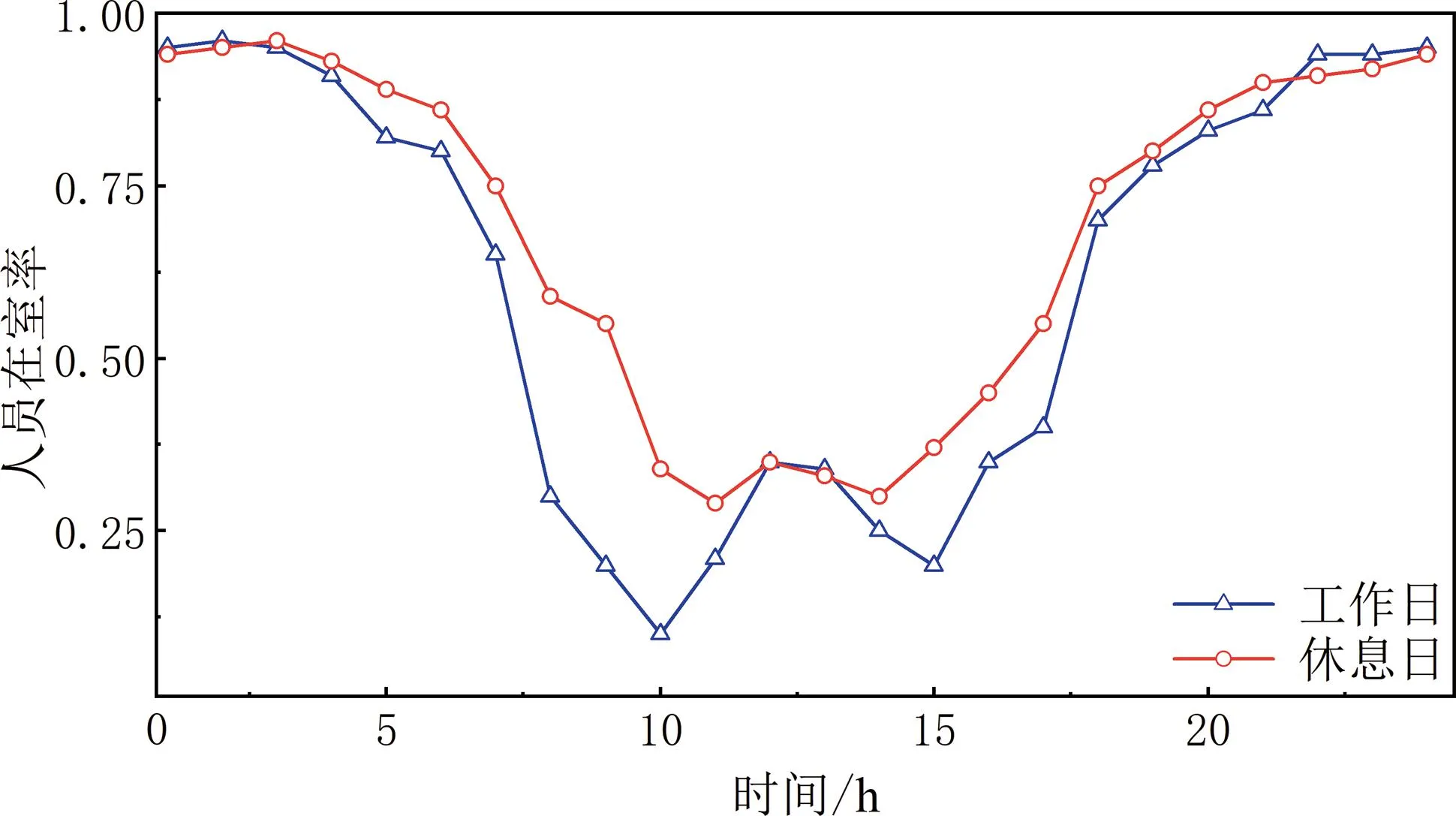
图2 人员在室率-时刻表

表2列出了28个输入参数的详细信息和变化范围,包括建筑围护结构和能源控制系统。选择这些输入参数主要基于其对建筑碳排放和室内热舒适度的共同影响[12-15]。

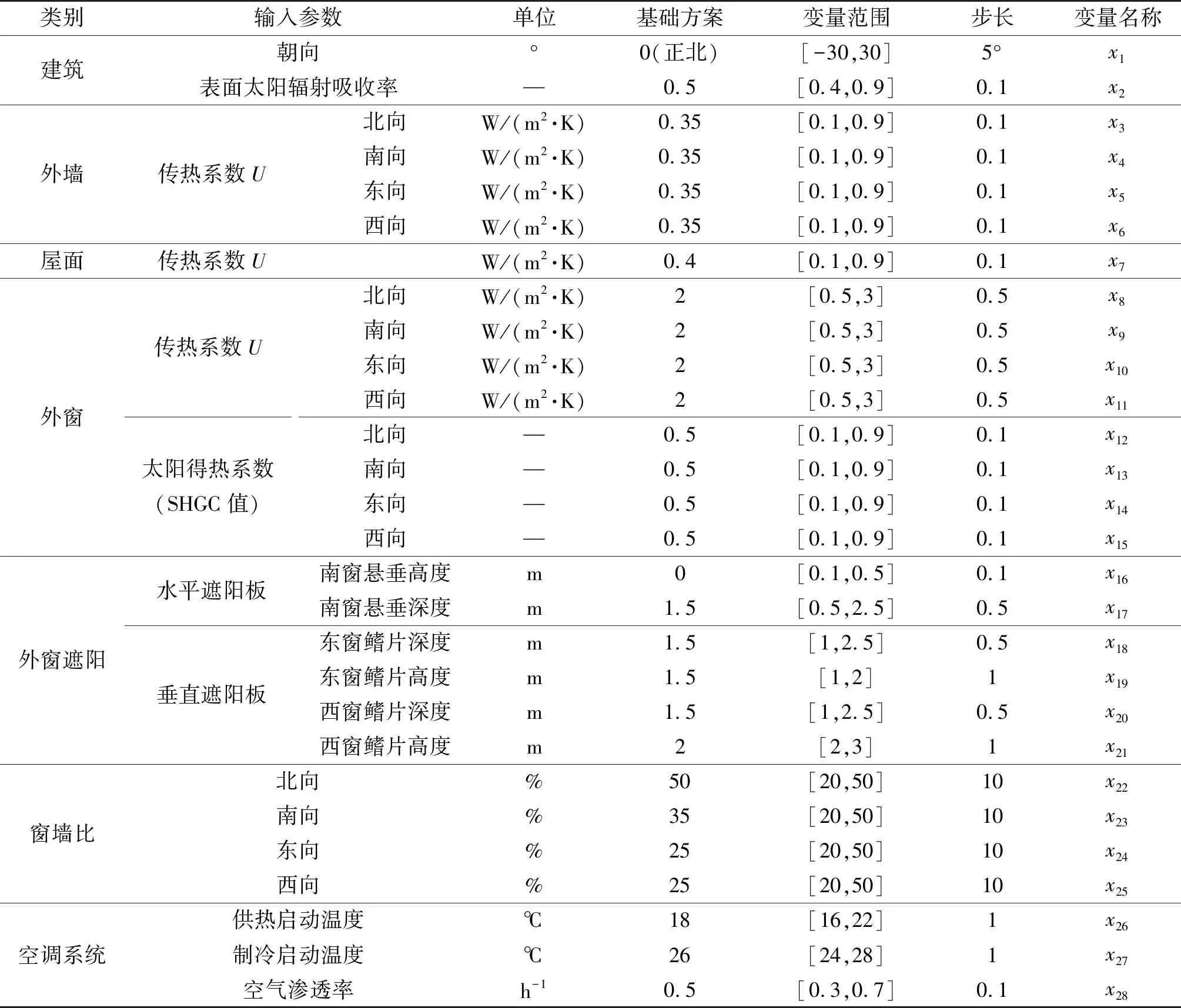
表2 建筑碳排放与室内热舒适度的主要影响参数

在确定输入参数及其变量范围后,通过将其进行排列组合,总共生成6.354×1017个案例样本。再分别使用5种不同的蒙特卡洛采样方法(包括eFast,LHS,Random,Sobol和Morris)对总样本进行采样,不同方法采集的案例样本数量均为此方法的最小需求。最后,使用JEPlus平台驱动EnergyPlus完成对案例样本结果的模拟收集,输出为年碳排放总量和年不舒适总时间。基础方案为基础建筑模型所对应输入参数值的合集。

1.2 定义目标参数

1.2.1 建筑年单位面积碳排放量 以建筑碳排放量与热舒适度为优化目标,其中,由于输入变量的改变对建造及拆除阶段的建筑碳排放影响较小,因此仅考虑建筑使用阶段所产生的碳排放量。

在计算运行阶段碳排放总量时,使用中国建筑碳排放计算标准:GB/T 51366—2019[15],并根据不同类型的能源消耗量和碳排放因子来确定总碳排放量。但由于无法通过建筑碳排放的绝对值比较不同建筑的碳排放强度,因此将碳排放总量转化为每年每单位面积的碳排放量作为目标函数,每单位面积的年碳排放量的公式如下:

(1)

(2)

式中:CM为建筑运行阶段单位面积碳排放量(以CO2计算),kg·m-2;A为建筑面积,m2;Ei为建筑第i类能源年消耗量,a-1;EFi为第i类能源的碳排放因子;Ei,j为j类系统的第i类能源消耗量,a-1;ERi,j为j类系统消耗由可再生能源系统提供的第i类能源量,a-1;i为建筑消耗终端能源类型;j为建筑用能系统类型;Cp为建筑绿地碳汇系统年减碳量(以CO2计算),kg·a-1;y为建筑设计寿命。

1.2.2 室内热舒适度 使用EnergyPlus中最常用的基于Fanger理论的预测平均投票(PMV)方法来评价热舒适度,该方法的主要依据为空气温度和相对湿度。室内居住者使用动态服装ASHRAE55模型,活动强度默认为静坐,70 W/m2。

由于MOEA/E,NSGA-Ⅱ和NSGA-Ⅲ三种算法的优化标准是最小化所有目标函数,因此,将目标函数由舒适时间转化为不舒适时间。

TN=8 760-TC,

(3)

式中:TC为全年室内热舒适时间;TN为年度室内热不舒适时间。

1.3 灵敏度分析

选择对建筑碳排放与热舒适性影响力较大的参数是提高BPNN精度与效率的重要步骤,灵敏度分析方法能有效量化各参数的影响力。然而,使用不同的灵敏度分析方法得到的输入参数灵敏度有所不同[16],因此,本文综合多种灵敏度分析指标量化各参数对优化目标的影响。如表3所示,将不同的采样方法与灵敏度分析方法相结合,为每个输入参数提供18类灵敏度分析指数。

表3 灵敏度分析指数

结合多个灵敏度分析指数,综合灵敏度计算方式如下:

(4)

式中:SA为不同指数的灵敏度总值;x为输入参数;n为影响因素的总数;y为输出目标值,包括单位面积建筑碳排放和年室内总热不舒适度小时数;z表示灵敏度分析指数;SA(x,y.z)为灵敏度分析指数结果的值;SAP(x,y,z)为灵敏度百分比。以此建立灵敏度百分比SAP(x,y,z)的搜索矩阵。矩阵的行向量表示同一种灵敏度分析方法但输入参数不同,列向量表示同一个输入参数但灵敏度方法不同。

(5)

(6)

最后,鉴于每个输入参数对碳排放和室内热舒适度的影响同等重要,建筑性能综合影响力可通过式(7)计算:

(7)

1.4 反向传播神经网络训练与验证

1.4.1 反向传播神经网络 BPNN是一种典型的前馈神经网络,图3是其示意图,典型的BPNN模型有3层:输入层、隐藏层和输出层。输入层的神经元,由经过1.3节筛选过后的参数组成,输出层的神经元是“建筑年单位面积碳排放量”和“室内年热不舒适时间”。隐藏层的神经元数量由试错法确定,该方法基于BPNN预测的平均相对误差来进行评估。选择最佳隐藏层数量至关重要,数量过少将导致BPNN存储信息的容量不足,数量过多会引起BPNN学习过载。

图3 神经网络示意图

1.4.2 模型的训练与验证 样本中70%的案例用于BPNN的学习训练,其余30%用于BPNN的验证。为评估预测模型的准确性,使用平均绝对误差(MAE)、均方根误差(RMSE)和回归系数(R2)作为评估参数,计算公式如下:

(8)

(9)

(10)

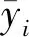
若MAE和RMSE的数值越低,R2值越高,则表示预测值与实际值越相似[17]。其中,若MAE在逐次迭代中保持稳定,则认为训练收敛。为提高BPNN的预测性能,使用遗传算法对BPNN的初始权重进行优化,经过29个阶段的训练后,显示MAE逐渐变小,并不再改变。同样,BPNN预测与EnergyPlus模拟结果之间的回归系数R2接近于1,证明了预测模型的可行性。

1.5 多目标优化问题定义

为快速准确地进行算法寻优,将高精度的BPNN取代传统的数学函数,作为多目标优化算法的目标函数,最小化室内热不舒适时间和建筑碳排放量,Matlab中执行算法时优化问题定义如下。

(11)

式中:f1(X)为目标函数碳排放量;f2(X)为目标函数热舒适度;X=(x1,x2,…,x27,x28)为输入变量。

分别利用MOEA/E、NSGA-Ⅱ和NSGA-Ⅲ三种优化算法进行多目标优化,搜寻最佳解决方案。

2 结果与分析

2.1 采样方法分析

分别使用5种采样方法对输入参数进行采样,结果如图4所示。

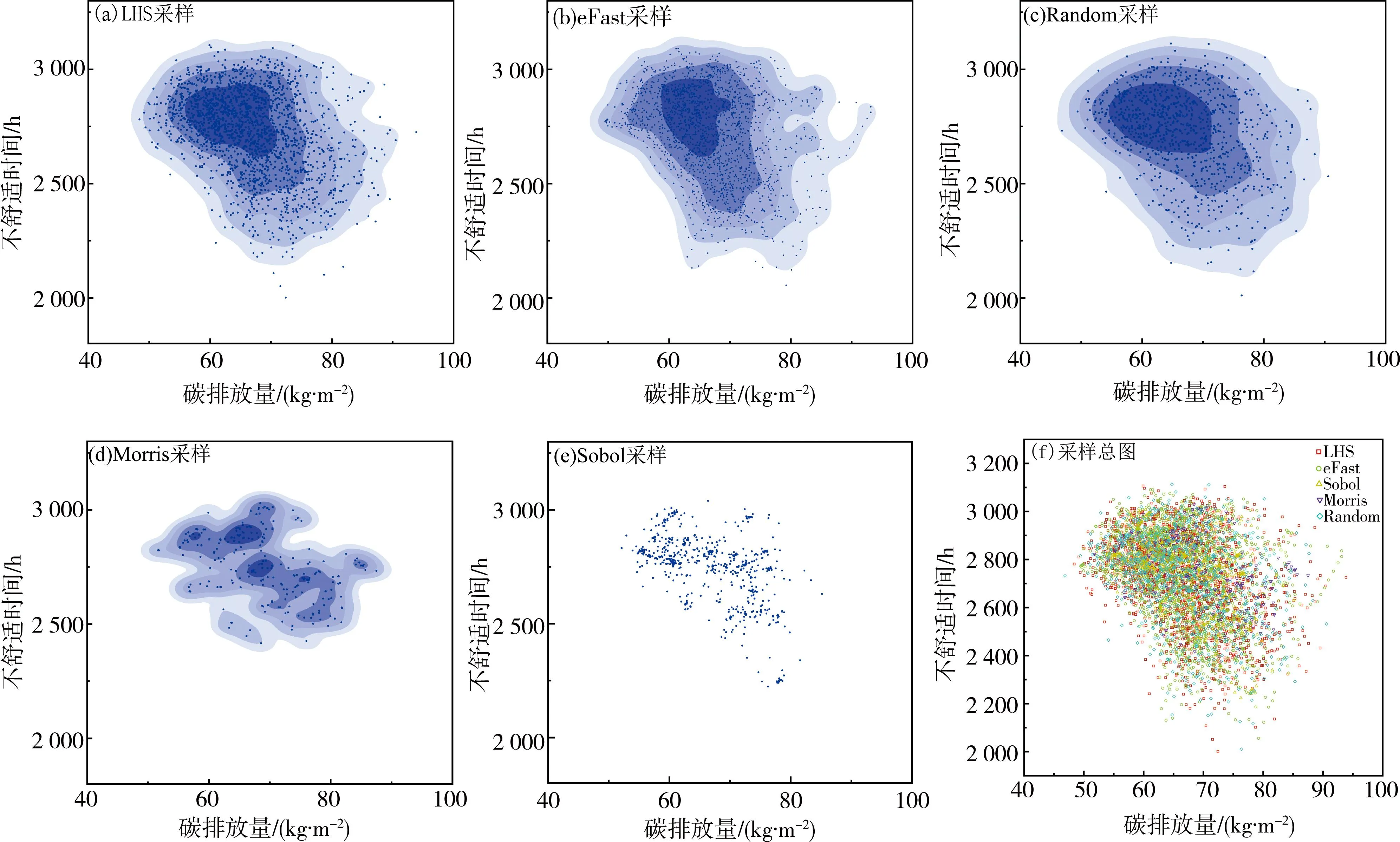
图4 采样结果

由图4可知,5种采样方法表现各有差异。其中,Sobol模拟采样数据与其他方法相比具有不同的分布,没有明确的质心。Random模拟采样数据分布最均匀。Morris分析方法与其他方法不同,每次采样依次仅改变一个参数,每个参数采样一次,在模拟中仅进行了270次采样,样本数量较小,但同样具有适用的搜索空间。LHS模拟采样与Random采样分布相似,但LHS具有最宽的变化范围,单位面积年碳排放量的范围为46.84～93.85 kg·m-2;室内热不舒适时间范围为2 001.33～3 113.56 h。

2.2 灵敏度分析

综合18种灵敏度分析指标后,各个输入参数对碳排放与热舒适度的影响力排名如图5所示。由图5可知,在使用拉丁超立方采样LHS和随机采样Random时,PEAR,SPEA,PCC,PRCC,SRC和SRRC的分析指数结果相似,但PCC和PRCC对冷热启动点、渗透速率、窗墙比等排名靠前的参数的影响力相差不大。Smirnov对不重要影响参数的评价过高,例如水平遮阳板距离外窗的高度、屋面太阳吸收率等。Fast和Sobol对影响参数的区分度较大,最大值与最小值之间存在显著差异,其中,制冷启动点的影响百分比高达33.98%,而不重要的影响参数却接近于零。eFast的供热启动点与其他方法的值相比差异较大,影响力百分比较低,而屋顶隔热的影响程度较高。Morris分析方法有别于其他方法,每次采样依次仅改变一个参数,每个参数采样一次,在模拟中仅进行了270次采样,但其灵敏度分析结果与1.3节中提出的综合灵敏度方法的结果十分相似。

图5 输入参数灵敏度百分比排名

利用18种灵敏度分析方法分别评估各参数对碳排放与热舒适度的影响,并将各方法所得影响力取平均值,按降序排列,其结果见图5最后一列。后续研究将去除平均影响力较小的9个输入参数,包括南窗悬垂高度、表面太阳辐射吸收率、东西窗鳍片深度、西向窗墙比、东西窗鳍片高度及东西窗传热系数U。

2.3 采样分析与BPNN模型验证

为提高预测模型的准确性和效率,在建立BPNN预测模型时,分析比较了不同抽样方法的准确性,其结果如表4所示。

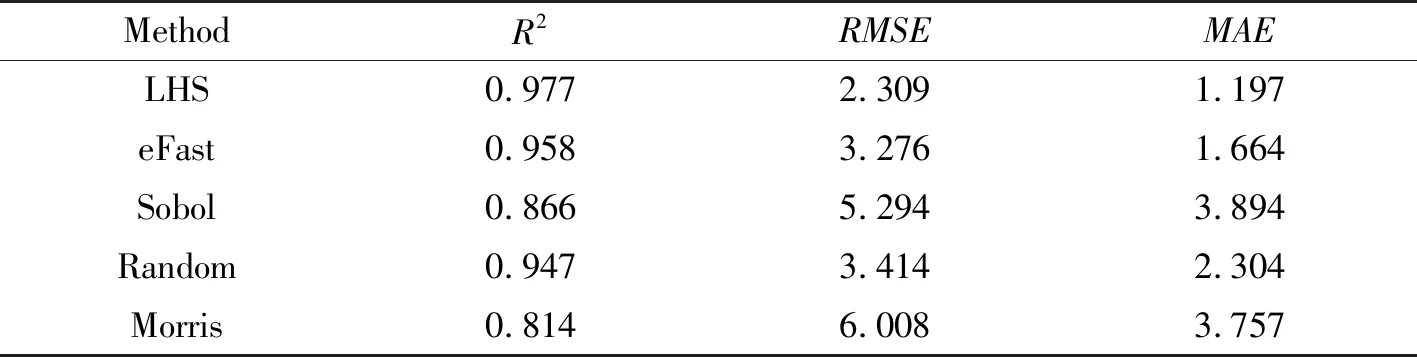
表4 BPNN预测准确性

由MAE,RMSE和R2三类指标结果可知,应用LHS抽样方法的BPNN预测性能表现最优,其他抽样方法对应的BPNN模型预测性能相对较弱。因此,在建立BPNN建筑性能预测模型时,利用LHS抽样所得的训练数据集可在最大程度上提高BPNN的准确性。

2.4 算法优化

将BPNN模型作为目标函数分别代入MOEA/E,NSGA-Ⅱ和NSGA-Ⅲ算法进行多目标优化,3种优化结果的帕累托前沿如图6所示。优化结果表明,MOEA/D相较于其他两种算法,其帕累托前沿存在一定差异,在优化过程中搜索空间较小,在建筑领域的优化效果弱于NSGA-Ⅱ和NSGA-Ⅲ,而NSGA-Ⅲ的优化效果与优化性能高于NSGA-Ⅱ。因此,选择NSGA-Ⅲ作为最佳优化方法。基本值为1.1节中所建立的基础建筑模型计算所得碳排放与热舒适度值。

2.5 帕累托详细值

通过最佳优化算法NSGA-Ⅲ对建筑模型进行优化,结果由表5可见,可为建筑设计提供全生命周期减碳的设计数值。

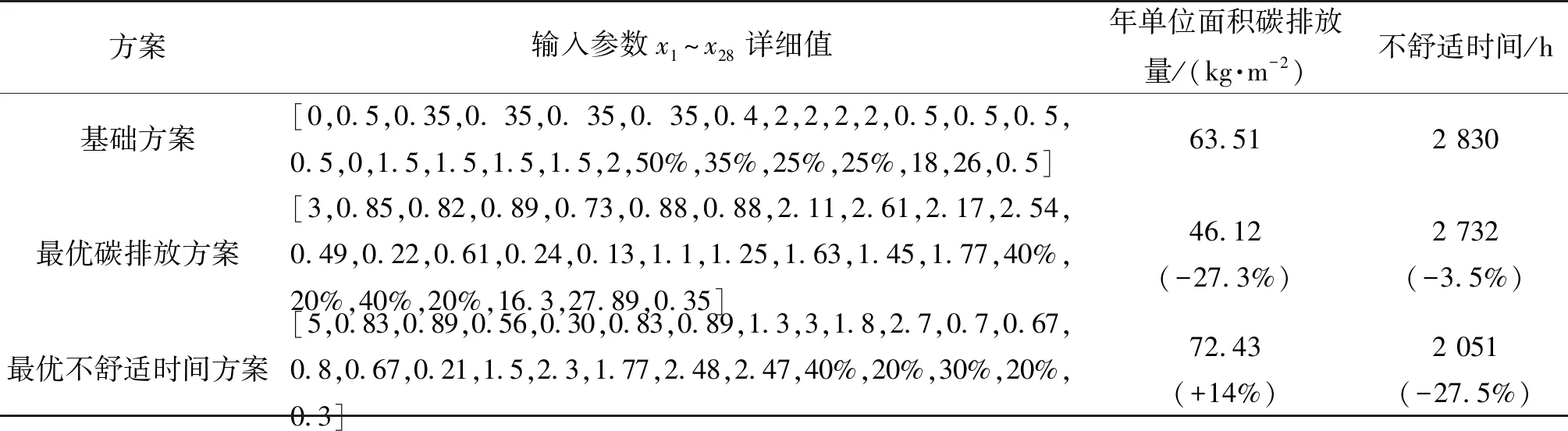
表5 帕累托详细值

由表5的帕累托最优解可见,在最优碳排放方案中,年单位面积碳排放量降低了27.3%,热不舒适时间减少了3.5%。在最优热不舒适时间方案中,年单位面积碳排放量增加了14%,热不舒适时间减少了27.5%。设计师可以权衡需要,在帕累托集中选择合适的方案。

结合图6和表5可知,长沙地区建筑最佳朝向的不是正北朝向,而是北偏东3°至5°,与基础点相比较,4个方向的窗墙比在优化之后均减少,且接近约束下限,说明在满足室内自然采光的条件下,较低的窗墙比可以有效降低建筑碳排放,提高室内热舒适度;当需要室内热舒适度最大化时,北窗的太阳得热系数(SHGC)应尽可能高,减少东向垂直遮阳。当建筑碳排放量最小时,西窗的太阳得热系数应尽可能低,东窗的太阳得热系数尽可能高,并加强西向的垂直遮阳,将各方向窗口传热系数设置相同且尽可能低;在保证建筑室内空气更新的前提下,建筑的气密性应该尽可能高;建筑表面的太阳吸收率最佳值与初始基础值相比明显减少,特别是屋顶和东墙,建议使用高反光涂层材料。

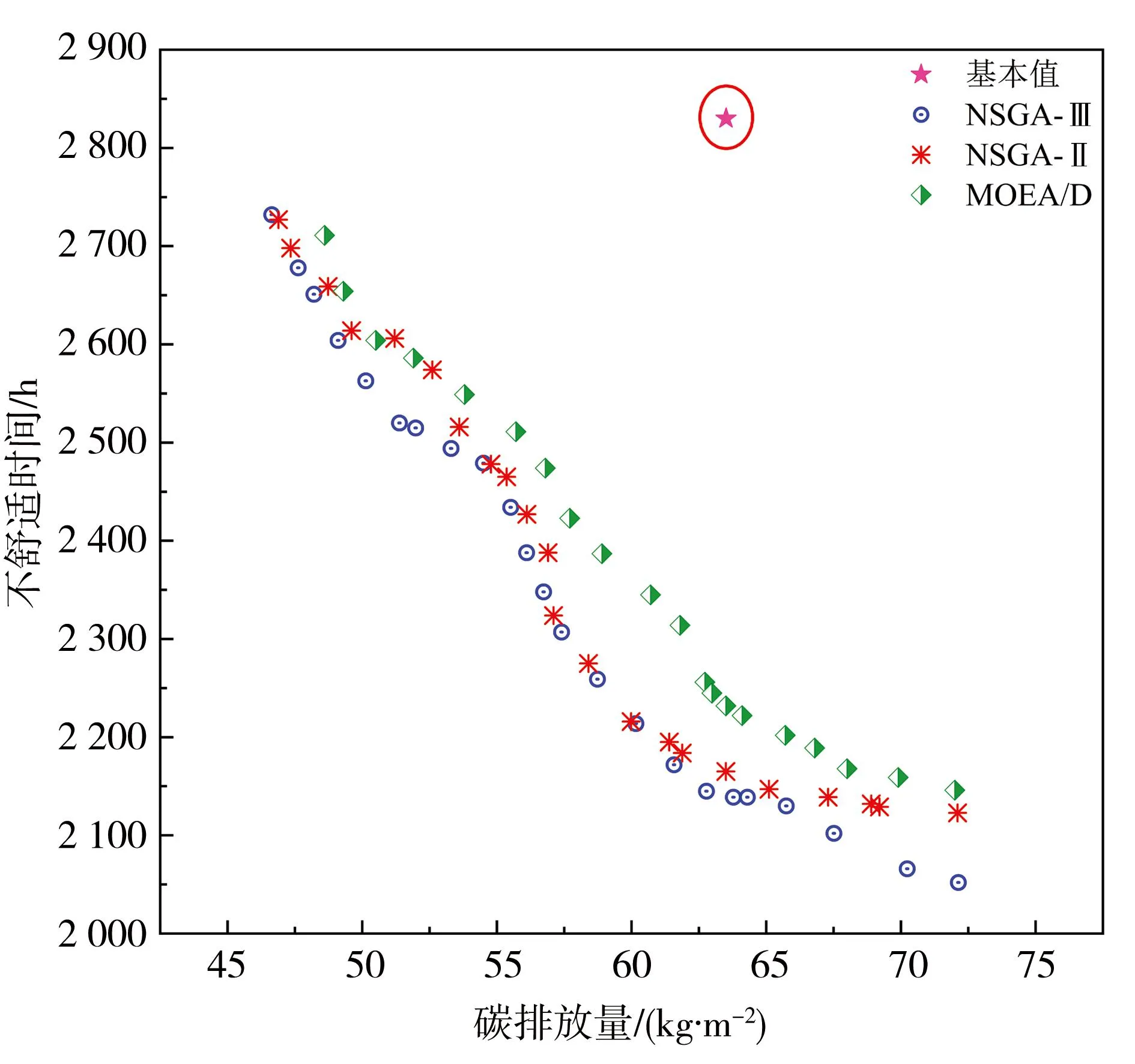
图6 帕累托前沿

3 结论

为减少建筑碳排放量,增加室内热舒适度,提出一种基于反向传播神经网络(BPNN)与优化算法相结合的综合优化框架。首先,运用5种抽样方法采集样本,为BPNN提供全面与高效的训练学习样本,运用综合灵敏度分析方法筛除低影响力参数,根据多类指标评价BPNN模型不同训练学习样本下的预测精度。其次,将最佳BPNN模型分别与MOEA/E,NSGA-Ⅱ和NSGA-Ⅲ相结合进行多目标优化,对其优化结果进行对比分析后确定性能最佳的优化算法。最后,将前文选择的最优架构应用于长沙市公寓楼,验证了该方法的有效性。得到以下结论:

1) LHS抽样方法可获得全面且高效的数据集,以供BPNN实现高精度预测,R2可以达到0.977,RMSE为2.309。

2) 基于帕累托前沿的比较分析,NSGA-Ⅲ的优化性能高于NSGA-Ⅱ和MOEA/E,NSGA-Ⅲ拥有更大更广泛的搜索空间,但目前其在建筑领域应用不广泛。

3) 论文提出的最优碳排放建筑构造参数,与测试的基础建筑相比较,全年建筑单位面积碳排放量减少27.3%,热不舒适时间减少3.5%。表明所提方法在减少建筑碳排放和提高热舒适度方面具有较好效果。