一维异质结构的瞬态热整流效应*

赵建宁 魏东 吕国正 王子成 刘冬欢†

1) (北京科技大学数理学院,磁光电复合材料与界面科学北京市重点实验室,北京 100083)

2) (中国空气动力研究与发展中心计算空气动力研究所,绵阳 621000)

3) (北京科技大学高等工程师学院,北京 100083)

瞬态条件下的热整流有广阔的实际应用背景,本文建立了一维板状复合结构热整流器的瞬态热整流模型,并利用有限元方法研究了不同恒定热阻、不同界面间隙、周期性温度边界条件以及材料和几何参数对瞬态热整流效果的影响规律.研究结果表明,界面热阻的存在可以提高系统的瞬态热整流系数,而初始界面间隙的引入让瞬态热整流系数实现了量级的飞跃.通过几何以及材料参数的合理设置有利于优化结构的热整流效果,针对周期性高温边界条件,温差和频率的变化可进一步提升复合结构的热整流系数.本文所提出热整流机制可以指导瞬态下热整流器的优化设计.

1 引言

热整流是一种不同温度梯度方向上传热能力不同的非对称传热现象.自从Starr[1]于1936 年在氧化铜中发现这种不对称传热机制以来,热整流一直是热量调控研究的一个热点.热二极管是热整流效应的一种典型应用,一方面可以疏导系统多余热量,另一方面可以隔热,因此热整流机理及器件的相关研究在节能、热防护和热输运上有重要的应用价值[2,3],此外基于热整流机理的热二极管[4]、热三极管[5]和热逻辑电路[6]为热学计算机的实现、热交换器的设计和航天器热控制系统的开发提供重要的器件支撑.

稳态条件下热整流机理的研究涉及到材料热物性的非线性和各种不同的物理机制,包括不对称结构[7]和热传递方向[8,9]引起的热整流效果.对于经典的宏观异质结构热二极管,基于傅里叶传热定律的研究表明实现热整流的必要条件是材料热导率为温度或空间的函数[10],其中利用两种材料热导率随温度变化的不同产生热整流的机制最为常见[11,12],通过温度梯度来调控双段式复合结构的等效热导率从而在不同方向上影响热传输能力,基于此的热整流机制也在实验中得到论证[13].热整流器的研究也逐步从实现热整流效果转换为优化热整流效果,研究发现通过调节材料热导率的温度相关性来优化热整流效果的设计是可行的[14-16].与此同时,结构的不对性也成为实现热整流的一个重要手段,采用变截面结构结合材料热导率的温度相关性可以实现热整流,比如多孔结构[17]、金字塔形[18]、双矩形[19]、圆柱状和球形热整流器[20,21].在非对称传热的热整流机理研究中,界面的接触热阻也是影响热整流效果的一个重要因素.研究表明,界面热阻的存在可以增大正、反向情况下热流量的差异,从而在经典双段热整流器的基础上优化热整流系数[22,23].考虑到界面热阻极大地受到界面应力、界面间隙和界面形貌的影响,应用热膨胀效应定向控制界面热阻也可以优化热整流效果[24,25].在热弹性系统中由外力引起结构应变的非均匀分布,从而改善结构的热导率,也可实现结构的热整流效果[26,27].此外,利用复合结构不同材料热导率和热膨胀系数的差异性,通过热膨胀实现热开关来调控界面热阻,也可以实现热整流系数的最优化[28,29].在微纳米材料器件中,如纳米梯形板[30]、异质结碳纳米管[31,32]、带孔硅纳米薄膜[33]也是热整流效应的研究热点.

值得注意的是,此前的研究中绝大多数都假设热整流器处于稳态,而在实际应用中热环境是动态变化的,比如热控应用中芯片的生热过程,对于热环境随时间变化时的热整流研究目前还刚刚起步,此时热整流不仅受材料热导率的影响,还受其比热容的影响.瞬态异质结构的瞬态热整流效果最早是由Herrera 等[34]于2017 年的研究结果表明比热容效应可以提高初始瞬时的热整流系数,合理选择材料热扩散率和热导率可以提高瞬态下的热整流效果.进一步的理论研究表明固态磁热制冷循环的异质结热二极管的最大热整流系数可以达到稳态条件下的295 倍,其平均热整流可能大于稳态值[35].而基于热导率和比热容时空调节机制的热波二极管也获得了大于86%的热整流系数[36].如果热二极管的边界条件随时间变化,此时瞬态热整流机理的研究更具有实际意义.Zhang 等[37]基于热二极管针对随时间变化的废热进行了回收利用,通过实验验证了俘能效率的提高,Shimokusu 等[38]研究了周期性变化的温度边界条件下的瞬态热整流效果.

可以看出,虽然目前针对热整流器件开展了的大量研究,但是考虑瞬态热环境的热整流研究相对较少,如何在瞬态热传导过程中实现热整流的最优化,具有十分重要的研究意义.本文研究了瞬态热环境下热整流器的整流效果,重点研究了界面应力和界面间隙相关的界面热阻对一维复合结构热整流效果的影响,给出了各种关键因素对热整流系数的影响规律,揭示其影响机理,为实际热整流器件的设计提供重要的理论参考.

2 瞬态热整流理论模型

2.1 问题描述

热整流器的物理模型如图1 所示,该热整流器由两个板状结构对接在一起.界面为非理想接触,存在界面热阻.当整流器的左端面给定高温边界条件TH且右端面给定低温边界条件TC时,热流从左端面流向右端面,为正向温度边界条件.当左右互换温度边界后,热流从右端面流向左端面,为反向温度边界条件.这里忽略结构y和z向的热传导,仅考虑轴向的一维热传导.

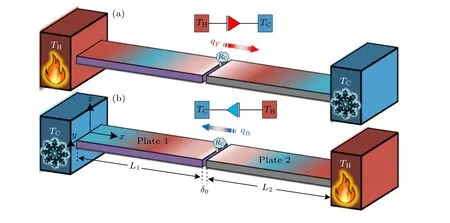
图1 复合结构热整流器模型 (a) 正向温度边界;(b) 反向温度边界Fig.1.Composite structure thermal rectifier model: (a) Forward case;(b) reverse case.

对于稳态热整流,可以合理利用材料热导率的温度相关性,即结构1 的材料热导率随温度升高而增大,而结构2 的材料热导率随温度升高而降低,当热量正向流动时,结构1 处于高温状态,结构2处于低温状态,此时结构等效热导率较高,有利于热量的传递.而热量反向流动时,结构等效热导率较低,从而阻碍热量的传递,这种等效热导率的差异产生了热整流效果.由于热量守恒,结构任意横截面上的热量是相同的,因此热整流系数可以定义为

其中,qF和qR分别为热量正向和反向流动时的热流密度.

对于瞬态热整流,在结构两端给定恒温边界条件的情况下,由于比热容效应,轴向热流量在不同时刻是不同的,本文以低温端热流为参考,定义瞬态热整流系数为

式中,qF,C(t) 和qR,C(t) 分别表示在正向和反向传热时低温端的热流密度.

2.2 理论模型

无内热源一维瞬态热传导问题的热量平衡方程为

其中,k是材料热导率,ρ和c分别为材料密度和比热容.下标1 和2 分别代表结构1 和2.由傅里叶定律,结构任意位置的热流密度为

结构两端的温度边界条件为

结构的初始温度条件为

式中,T0是结构初始温度.

在界面处,有热流连续条件:

同时,在接触界面处的界面热阻Rc为

其中,T1|x=L1和T2|x=L1分别是结构1 与2 在界面处的温度值,q|x=L1为界面处的热流值.

考虑到结构动力学响应的时间比瞬态温度场要小得多,因此这里假设结构位移场处于准静态.结构的平衡方程可简化为

考虑热变形的应力应变关系为

式中,E是材料弹性模量,u是结构轴向位移,α是材料热膨胀系数,Tref是热变形参考温度.

结构两端的固定边界条件为

在界面处,有应力连续条件:

同时,若界面处预先设置了初始界面间隙δ0,当初始界面间隙因热膨胀而闭合时,则应给定界面位移连续条件:

针对目前常见的材料,材料参数例如热导率、比热容、热膨胀系数等都具有温度的依赖性,同时复合结构的瞬态温度场、应力场都与界面热阻相关,因此有限元方程组是复杂的非线性方程组,需要进行迭代求解.本文空间域和时间域在数值上分别采用Galerkin 有限元格式和Crank-Nicolson 方法,其非线性迭代方法经过了准确性验证.

3 参数影响研究

界面热阻作为复合结构实现热整流效果的诱导因素,受多种因素的影响.无约束边界下,界面热阻主要和材料属性、表面形貌等相关(图2(a)),利用热界面材料可以定量的控制界面热阻(图2(b)).若复合结构约束两端面位移,当界面间隙闭合,界面热阻主要与界面压力有关,并随接触压力的增加而减小,这是由于较大的压力有助于提高实际的界面接触面积,从而增强界面之间的热传递能力(图2(c)),而当界面间隙没闭合,界面间隙之间的热量主要依靠空气热传递(图2(d)),图2 为3 种不同界面传热形式的示意图.

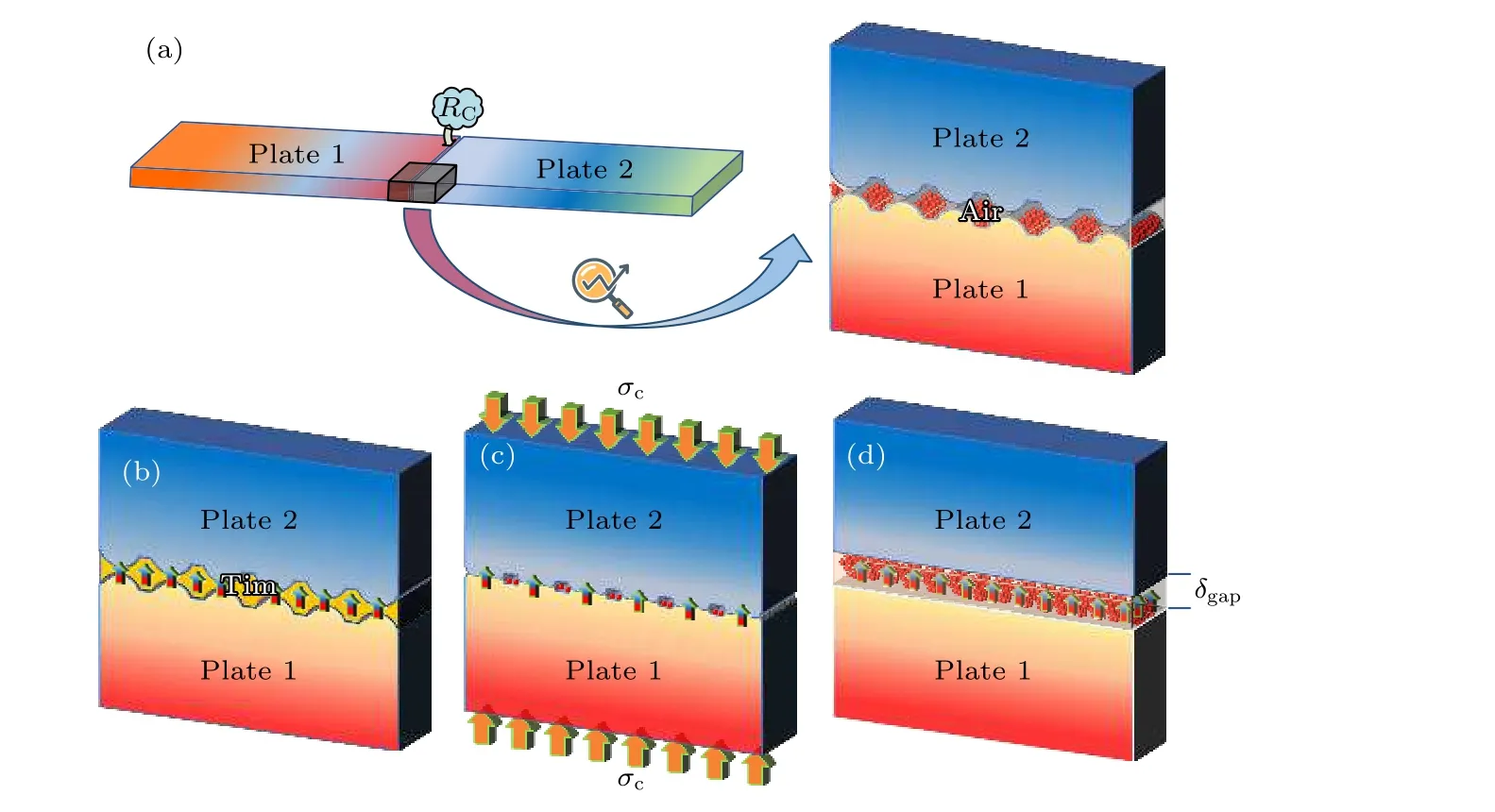
图2 不同的界面传热形式Fig.2.Different forms of interface heat transfer.

若复合结构无约束,考虑界面热阻Rc为恒定值R0,当复合结构两端被固定约束,则界面热阻模型参考铝和不锈钢的实验结果[39],如下所示:

其中,σc为界面接触应力(MPa),δgap为间隙大小,为界面空气的平均热导率.

在复合结构界面处,结构的界面间隙、界面应力一直在变化,因此模型的材料和几何参数也时刻影响着结构的位移场、应力场分布,导致界面热阻的数值时刻发生改变,从而引起结构温度场的重分布.因此在下文讨论中,首先给出了恒定界面热阻下的瞬态热整流效应,进而考虑基于界面应力、间隙相关的界面热阻,研究瞬态热整流系数随不同的边界条件、几何和材料参数的变化,揭示复合结构的热整流机理,通过改变初始界面间隙、参数优化等措施,调控复合结构的瞬态热整流效果.

3.1 恒定界面热阻的影响

本节利用铝和纯铁[40]作为复合结构热整流器结构1 与2 的材料,研究恒定界面热阻下的瞬态热整流效应.复合结构长0.16 m,宽0.016 m,两种结构等长,高低温端面温度固定并分别给定700 K和300 K,初始温度为300 K.图3 分别给出了界面热阻为0,1×10—4,1×10—3,5×10—3m2·K·W—1时的瞬态热整流系数以及正反向低温端的热流变化.

材料的热导率k影响了整体结构的热传导能力,而比热容c和密度ρ主要决定复合结构吸放热的能力,通过热扩散率αk=k/(ρc) 可以描述复合结构的热扩散能力.从图3 看出,随着界面热阻的增大,初始阶段的热整流系数增大,随着时间的推进,在传热后期当趋于稳态阶段,界面热阻为1×10—3m2·K·W—1时热整流系数最大.这是由于界面热阻会导致界面两侧温度跳变,使得结构1 的高温区域和结构2 的低温区域同时扩大,而铝的热扩散率几乎随温度升高而增大,铁则相反,因此界面热阻的存在除了阻碍界面热量传递,在一定的程度上也增大了正反两个方向上的瞬态热量扩散能力的差异,同时在传热后期增大了正反方向等效热导率的差异,从而增强复合结构的热整流效果.对于界面热阻为5×10—3m2·K·W—1的情况,在瞬态传热初期,界面热阻越大,其诱导的热扩散能力的差异增大,正反向低温端热流差值较大,因此热整流系数增大.在瞬态传热后期趋于稳态阶段,此时结构的等效热导率占据主导地位,热扩散能力的差异表现得较不明显,而过大的界面热阻严重阻碍结构的传热能力,即5×10—3m2·K·W—1的界面热阻远大于结构1 与2自身的阻抗,使得正反向等效热导率接近,低温端的热流差值较小,因此热整流系数快速的降低,从而导致热整流系数趋于1.12.由此可见,在瞬态传热初期,可提高界面热阻实现复合结构热整流效果的增强,而传热后期合理的界面热阻也能适当提高热整流系数.

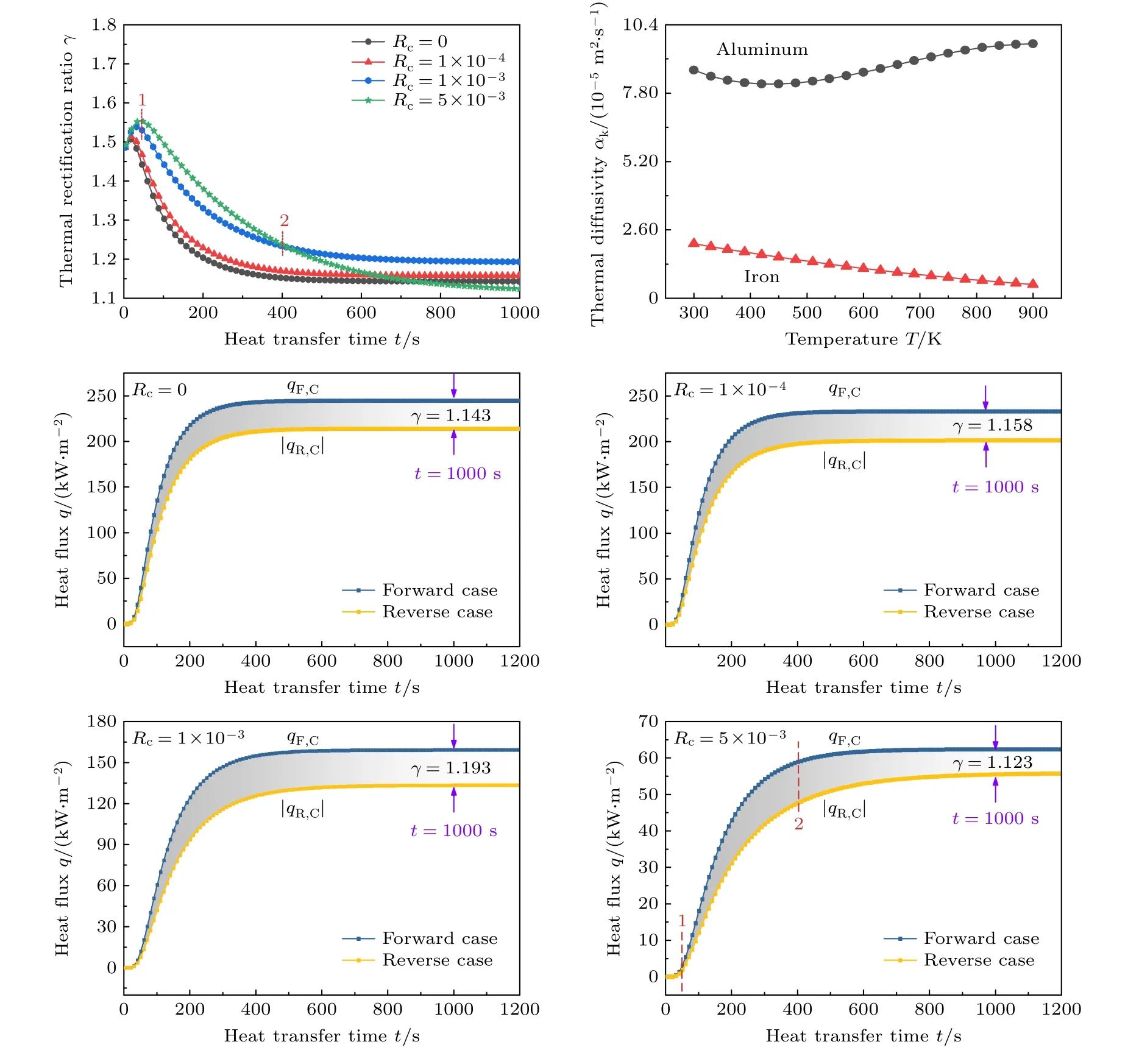
图3 不同界面热阻下的瞬态热整流系数Fig.3.Transient thermal rectification ratio with different interface thermal resistances.

实践中大多数热系统会经历周期性行为,例如加热/冷却,或者晶体管边界条件的瞬时变化,保持上述结构几何、材料参数不变,将高温边界条件设定为TH(t)=700 K-ΔTcos(ωt),其中 ΔT=200 K,ω=0.05,图4 给出了周期性变温边界条件下不同界面热阻对瞬态热整流系数的影响规律,同时给出无界面热阻时结构低温端的热流和高温边界条件的变化趋势.

从图4 可以看出,在周期性温度边界条件下,热整流系数快速的达到一个极大值,随后热整流系数逐渐降低并有一定幅度的振荡.合理界面热阻的增大可以增大复合结构的最大热整流系数及其振荡的幅值.由于比热容效应导致热量传递的延迟性,使得温度边界变化和热流变化并不同步.与此同时,由于正反向热流变化也不同步,因此在正反向传热时低温端热流并不总是同时达到波峰或波谷,当正向低温端热流达到波峰,而反向低温端热流达到波谷时,此时瞬态热整流系数最大.

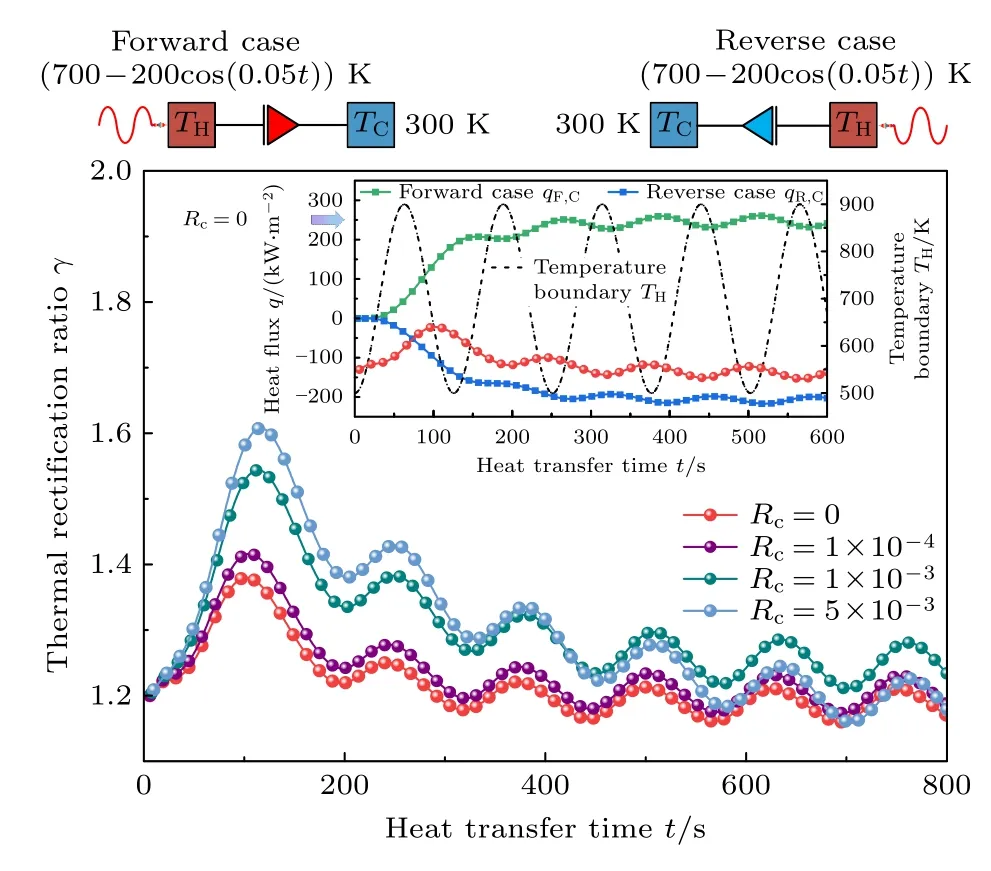
图4 周期性变温边界条件下界面热阻对瞬态热整流系数的影响Fig.4.Effect of interface thermal resistance on transient thermal rectification ratio with periodical temperature boundary conditions.

3.2 初始界面间隙的影响

根据3.1 节恒定界面热阻的研究结果,其瞬态热整流系数最大约为1.6,热整流效果较弱,因此本节引入一种热接触开关式的热变形机理,引入初始界面间隙调控界面热阻从而实现热整流系数的最优化.研究模型与3.1 节相同,结构两端面位移固定,热变形参考温度为300 K.图5 给出了不同初始界面间隙下瞬态热整流系数的变化规律,图6进一步给出了初始界面间隙δ0=0.6 mm 时,热整流器各个关键物理量的动态变化过程.

从图5 可以看出,对于不同的初始界面间隙,由于比热容效应,瞬态热整流系数都是先增大后减小,合理的初始界面间隙比如0.6 mm 或0.8 mm,可以提高复合结构瞬态热整流系数一个数量级.这是因为界面间隙在正向传热过程中闭合,而反向传热时界面间隙不能闭合,从而导致正反方向较大的等效热导率差异.当初始界面间隙较小例如0.2 mm 或0.4 mm,无论正反向传热界面间隙在100 s 以及380 s 后都将闭合,因此热整流系数降为1 左右,同理,过大的初始界面间隙在正反向传热时都不会闭合,也导致热整流系数在1 左右.对于初始界面间隙为0.6 mm 的情况,从图6(a)看出,正向界面间隙在25 s 后闭合,此时界面处产生了界面应力,并随时间逐渐增大如图6(b)所示,从而导致基于应力相关的界面热阻急剧下降几乎趋于0,如图6(c)所示.而反向传热时界面间隙逐渐减小,但一直处于张开状态,此时无界面应力,但界面间隙的存在极大地提高了界面热阻,因此导致正反向低温端热流的差值较大如图6(d)所示,从而提高了热整流系数,并在传热后期依然保持相对较高的热整流系数.由此可见,当初始界面间隙处于合理的范围内时,即可以使得正向界面间隙关闭反向界面间隙一直张开时,此时初始界面间隙越大,复合结构整体的热整流系数越大.

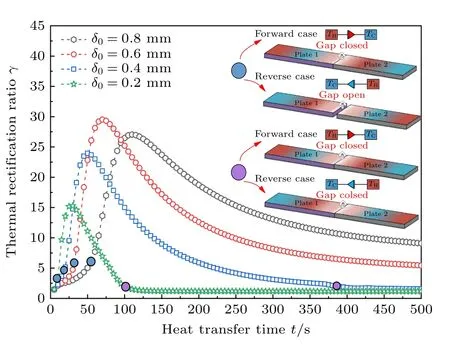
图5 不同初始界面间隙下的瞬态热整流系数Fig.5.Transient thermal rectification ratio with different initial interface gaps.

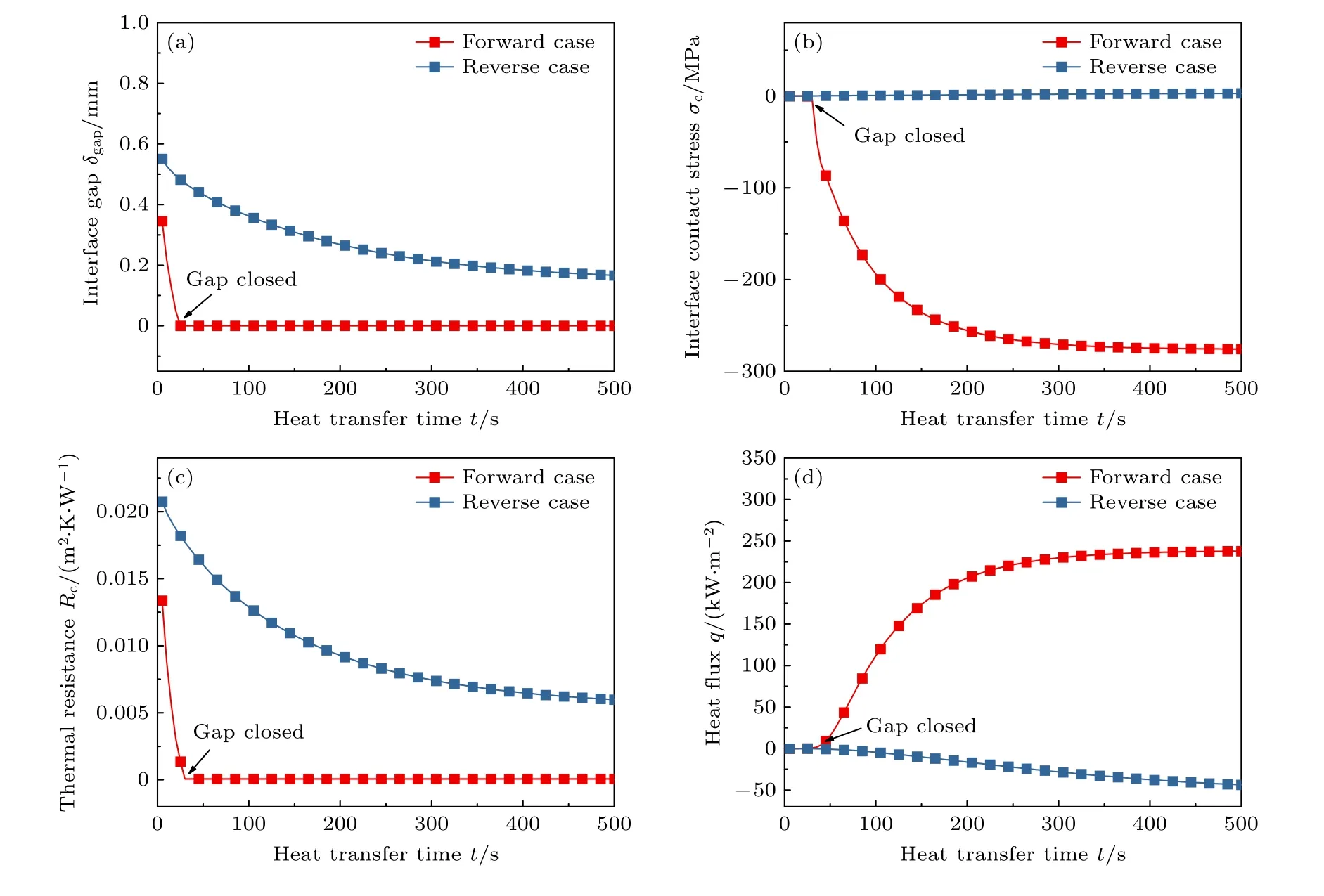
图6 初始界面间隙为0.6 mm 时热整流器关键参数的瞬态响应 (a) 界面间隙;(b) 界面接触应力;(c) 界面热阻;(d) 低温端热流Fig.6.Transient response of key parameters in thermal rectifier with 0.6 mm initial interface gap : (a) Interface gap;(b) interface contact stress;(c) interface thermal resistance;(d) heat flux at cold side.

考虑随时间变化的高温边界条件TH(t)=700 KΔTcos(ωt),其 中 ΔT=200 K,ω=0.05,图7(a)和(b)给出了周期性变温边界条件下初始界面间隙为0.6 mm 时,低温端热流和界面热阻的变化情况,图7(c)给出了不同界面间隙对瞬态热整流系数的影响规律.

从图7 可以看出,与定温边界条件类似,不同的初始界面间隙导致不同的界面开合状态,初始间隙过大会导致界面间隙一直张开,而过小则会导致界面间隙一直闭合.在合理的初始间隙范围内,初始界面间隙越大,瞬态热整流系数越大,这是由于在反向界面间隙张开的情况下,初始界面间隙越大,则最终未闭合的界面间隙越大,从而增大了反向界面热阻,进而提高了热整流系数.对于0.8 mm的初始界面间隙,在周期性温度边界条件的影响下,两端较小的温差不利于界面间隙的闭合,因此正向传热时界面间隙会在张开和闭合状态之间切换变化,界面热阻从而出现了半波形曲线变化如图7(b)所示.对于0.6 mm 的初始界面间隙,随传热的推进,正向界面间隙关闭,反向张开.对于0.2 mm 的初始界面间隙,正反向界面间隙会很快关闭,因此热整流系数较低.

3.3 周期性温度边界参数的影响

本节研究模型与3.2 节相同,初始界面间隙为0.6 mm,研究周期性温度边界参数对瞬态热整流系数的影响.针对周期性高温边界条件TH(t)=700 K-ΔTcos(ωt),首先保持ω=0.05 不变,瞬态热整流系数随 ΔT的变化如图8(a)所示,复合结构的界面热阻与低温端热流变化如图8(b)和 (c)所示;然后保持 ΔT=200 K 不变,瞬态热整流系数随ω的变化如图9(a)所示;瞬态热整流系数随正余弦型周期性高温边界条件的变化如图9(b)所示.

图8 不同周期性条件参数 Δ T 下的瞬态热整流系数Fig.8.Transient thermal rectification ratio with different periodical condition parameters Δ T.

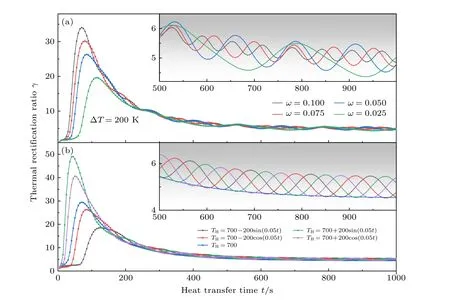
图9 不同周期性条件参数 ω 和高温边界形式下的瞬态热整流系数Fig.9.Transient thermal rectification ratio with different periodical condition parameters ω and high temperature boundary forms.

从图8(a)可以看出,对于0.6 mm 的初始界面间隙,周期波动边界参数 ΔT越大,瞬态热整流系数越大.边界参数 ΔT的增大提高了高温边界波动的幅度,由于铝和铁的热导率以及热扩散率的温度相关性,较大的边界温差有利于改善结构的传热性能.从图8(b)可以看出,初始界面间隙在传热过程中关闭,反向界面间隙一直张开,因此较大波动幅度的边界温差对于正向传热界面热阻的影响较小,但一定程度上会增大反向传热时的界面间隙,从而提高反向界面热阻.因此如图8(c)所示,结构传热性能的改变使得正向低温端热流向上波动幅度变大,而反向界面热阻的增大降低了低温端的热流,综合这两个因素的影响,边界参数 ΔT的提升可增强热整流效果.

从图9(a)可以看出,边界温度变化频率的改变不仅会影响热整流系数波动的频率,还会影响其波动的幅值,随着变化频率的增大,在初始阶段热整流系数增大,波动的幅度减小.如3.1 节研究结果所述,当正向传热时低温端热流为波峰,反向传热时低温端热流为波谷,此时热整流系数最大,而变化频率越大,热量传递波动越快,在相同的传递时间内,降低了热流曲线在周期内波谷和波峰的差异,由此热整流系数波动的幅度减小.

从图9(b)可以看出,初始阶段温差越大,瞬态热整流系数越大.与恒定高温边界相比,无论在正弦还是余弦的高温边界条件下,传热后期的瞬态热整流系数均大于恒定高温边界,且热整流系数波动趋势一致.因为反向界面间隙张开,在周期波动的高温边界条件下,界面热阻会随界面间隙的改变而波动下降,在一定的程度上阻碍热量的传递.因此针对特定的几何、材料参数、周期高温边界条件的引入,有助于复合结构实现更好的热整流效果.

3.4 材料与几何参数的影响

本节研究模型与3.2 节相同,周期性高温边界条件不变,即TH(t)=(700-200 cos(0.05t)) K,初始界面间隙为0.6 mm,研究几何和材料参数对瞬态热整流系数的影响.图10(a)给出了不同材料组合下瞬态热整流系数的变化趋势,图10(b)给出总长不变的条件下,不同长度组合结构的瞬态热整流系数的变化趋势.

图10 不同几何和材料参数对瞬态热整流系数的影响Fig.10.Effect of geometry parameter and material pair on the transient thermal rectification ratio.

从图10(a)看出,不管哪种材料组合的结构都满足正向传热时间隙闭合反向传热时间隙张开的条件,因此瞬态热整流系数普遍较大.两种材料的热膨胀系数差异性越大,界面间隙越容易满足正向闭合而反向张开的条件,从而导致可调节的预留界面间隙的范围越广.对于恒定界面间隙,在传热的后期阶段,瞬态热整流系数主要与组合结构的等效热导率相关,铜-钨组合结构的等效热导率相对较大,因此瞬态热整流系数较大.

从图10(b)看出,若复合结构总长度固定,铝结构越长结构热整流系数越大.这是由于铝的热导率以及热扩散率比铁大很多,因此其长度越长结构的等效热导率就越大.结构的等效热导率决定了正向传热时热流曲线整体的数值大小,而热扩散率改变瞬态热整流系数波动的幅度.另一方面,铝的热膨胀系数也较大,因此当铝结构的长度为0.04 m时,较低的温差以及较短的铝结构使得正向传热时界面间隙在开合状态之间周期性波动,从而正向界面热阻出现反复变化.由此可见,通过调节长度比和选用合理的材料组合有利于增强热整流效果.

4 结论

本文建立了复合结构的瞬态热整流模型,主要针对若干关键参数对瞬态热整流系数的影响开展了全面深入的研究,得到的主要结论总结如下:

1)合理的界面热阻,可增大正反向热扩散能力的差异,从而提高热整流系数,但过大的界面热阻会降低热整流系数.

2)通过设置初始界面间隙可以定向操控界面热阻,对于正反向传热情况,由于温度场不同导致的热膨胀量的差异,使得间隙出现闭合和张开两种状态,从而可以将瞬态热整流系数提高一个数量级.

3)几何和材料参数会影响组合结构的等效热导率,从而影响瞬态热传递后期的热整流系数.组合结构的等效热导率越大,则瞬态热整流系数越高.

4)瞬态热整流系数波动的幅值随着周期温度边界条件波动幅度的增加而变大,周期温度边界条件的变化频率不仅影响瞬态热整流系数变化的频率,还可以提升波动的幅值,从而实现更好的瞬态热整流效果.