教学要教出教师的“思想”*
潘龙生 (江苏省盐城市第一中学 224005)
1 背景与问题
2021届高三江苏省盐城市第三次模拟考试考查了下面这个问题:
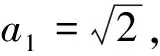


这道题对于教师来讲不是难题,笔者与同事交流发现,教师普遍能想到两种主要方法:一是取对数转化为等比数列,先求出数列的通项公式再证明;二是用数学归纳法证明,既可以用数学归纳法直接证明结论,也可以借助数学归纳法得出通项公式后再证明结论.当然,还有很多教师想到其他方法.
对一道常规的高中数学题,为什么学生与教师的解题水平反差如此之大?值得思考.
2 分析与对策
现在想来,这道题对学生来讲,也确实不易!新课标对数学归纳法不作要求,教师也基本没讲(笔者也是),学生当然不能运用这种方法;对数运算的基本公式,学生虽然熟悉,但取对数这种方法平时运用较少,加之学生对“对数”的认知不足,以致特定情况下想不到取对数.
至此,也就不难理解“学生与教师为什么有如此之大的反差”了.教师是按照“课标、高考”的要求教“课本”,并没有教出教师自身的“思想”.对数运算教学,也就是分析得出基本公式,然后运算训练,没有让学生明白学习对数的意义,也没有让学生理解对数有简化运算(降次)的作用;数学归纳法不作要求,也就不讲,把精力都放在重点内容的讲解上.
本文研究的这道考题,其超低正确率的原因可能是之前没有教出教师的“思想”.就笔者而言,要反思今后的教学,要结合教材、课标、高考向学生充分展示自己的“思想”.如此反思,笔者就这道考题的教学提出自己的教学思想.
2.1 教理解
问题1同学们,本次模考的数列解答题正确率很低,其重要原因是没有想到“取对数”这一方法.想不到“取对数”,说明大家对“对数”的认识还不够深刻.因此,先请同学们思考:学习“对数”的意义是什么?
告诉学生“取对数”,他们当然能顺利完成这道数列题,但下次再碰到类似的问题,他们还能想到“取对数”吗?这就难说了.倘若能让学生深刻认识“对数”、理解“取对数”的内涵,下次再遇到类似的问题时想到“取对数”的人数肯定能多出不少!
学生都知道,学习了“对数”之后可以将指数式转化为对数式.那就要让学生思考:为什么要将指数式转化为对数式?仅仅告知学生“对数能够简化运算”肯定不行,他们将信将疑,印象不会深刻,必须要让他们体验感悟.比如,“同学们都知道250比较大,那它到底有多大?是多少位数的整数呢?”令t=250,取对数lgt=50lg 2,指数运算就转化为乘法运算,只要知道lg 2≈0.301 0,便得lgt≈15.05,即t≈1015.05=100.05×1015,显然1<100.05<10,所以250肯定是一个16位数.这个实例说明,对数能够估算较大的指数值,取对数能够降次,能够极大地简化指数运算.如果是新授课,还要给学生介绍对数产生的背景,必须要让学生明白学习对数的意义.
2.2 教方法
数学归纳法等经典数学方法,已从必修数学教材中删除,若教师不补充,学生将来在大学阶段又不学,是不是有点遗憾?教师已具备的思想方法,考虑学生的接受能力,有选择地传授给学生,有何不可?
问题2数列问题是一类正整数问题,其证明题有时能运用一种重要的方法——“数学归纳法”证明.什么是“数学归纳法”呢?小时候,你们都数过正整数吧?后来,你们说:“我已经会数数了.”请同学们思考:你怎么确定你已经会数数的呢?
学生不难说出认为自己会数数的原因:虽然数不完,但总能顺次数下去.教师追问:怎么理解“能顺次数下去”?不难得出,当数出某个数时,一定能数出下一个数.最后师生总结出会数数的原理:首先能数第一个数,其次由前一个数总能数出下一个数.
由此,教师提出:能不能借用此思路证明“正整数命题M(n)成立”呢?学生能轻松说出第一步先证n=1时成立,需与学生说明,有些命题成立的初始值不一定是n=1,要根据实际情况完成第一步;对于第二步,要让学生反复想数数的核心原理“由前一个数总能数出下一个数”,即由n=k总能推出n=k+1,也即假设n=k时命题成立,并由此推理出n=k+1时命题也成立,从而得到正整数命题M(n)成立.这就是数学归纳法,也称第一数学归纳法.对于第二数学归纳法,可讲可不讲,若讲,则要等学生对第一数学归纳法较熟练的情况下再介绍.
由于学生初次接触数学归纳法,教师需要给学生示范证明.同时教师巡视指导,并选一些完美(或有一点瑕疵)的证明过程,通过投影展示点评.此后,再多用数学归纳法,学生定能接受!不一定非要让学生找出旧课本,给他们补充这一数学知识,教师根据自己的思想,合理设计教法,就可教给学生!
2.3 教变通


问题3说明,高中数学还要重视运算教学.要重视运算公式的推导教学、要重视算理分析教学、要重视运算演练.除此之外,还要重视运算“变通”教学.有些运算问题,学生死算得到答案,但耗费时间较长,就需要教师“变通”教学,要指引学生分析代数式的结构特征、要指引学生寻求合理的运算公式、要示范合理省时的“变通”运算.
3 反思与提升
教师教学,不能仅仅是翻译课本知识,更要教出教师自己的“思想”.只有贯穿思想方法,揭示本质的教学,才是有价值、高效的教学[1].要教出教材知识的理解,要通过教师合理的理解解读,让学生更容易接受新知识;要教出教材例题方法的合理性,不能生硬评讲教材上的方法,应该要通过教师自己的合理引导得出方法;要教出教材知识的宽度和深度,要能拓宽知识面,揭示其文化背景等,要能将知识引向深入,揭示其深刻的本质.如此等等,才能体现教师教的作用,学生接受的不仅仅是课本知识,更有教师的“思想”,这能体现课程标准提出的培养学生核心素养的要求,也能提高学生应对高考的能力.

