基于粒子群优化的双凸透镜缺陷Otsu阈值分割算法

戚云涛,曾寿金,方宇轩,蔡晓洁,沈庆梅

(1. 福建理工大学 机械与汽车工程学院,福建 福州 350118;2. 福建优恩立光电科技有限公司,福建 福州 350000)

双凸透镜是光学玻璃通过切割、研磨、清洗、镀膜等操作后得到的透镜,因加工技术的限制,不可避免地会出现一些如麻点、划痕等不同类型的缺陷[1]。根据《光学零件表面疵病》(GB1185-2006)规定的一般表面瑕疵要求[2],零件最大尺寸范围在10～30 mm的瑕疵面积公差为5 mm ×0.25 mm。本课题研究对象为直径14 mm的双凸透镜,通过目视观察的方法易受主观因素影响,很难准确辨别出缺陷类型和大小[3]。因此本课题依靠机器视觉和图像处理进行实时的缺陷检测,通过图像分割[4]将目标缺陷和背景区分出来,从而获取缺陷图像。

一般的图像分割算法包括阈值分割[5]、边缘检测[6]、区域生长[7]等。针对缺陷检测,常采用的算法主要有阈值分割和边缘检测。Otsu图像分割算法[8]通过计算两区域之间的最大类间方差值求出分割阈值,算法简单,但其计算量随着维度的提升而急剧增加、从而导致实时处理能力下降。因此启发式搜索优化算法也被引入图像分割中。其中受鸟群觅食启发的粒子群优化算法(particle swarm optimization, PSO)由于收敛速度较快、参数少、算法简单而被广泛应用于图像处理领域。但标准的PSO算法会出现早熟收敛,陷入局部最优的问题,需要进行改进和优化。郭宗建等[9]通过融入一种新的惯性权重并构建了一种新的极值扰动的方法,提高了粒子跳出局部最优的能力。Song等[10]在位置更新公式中引入约束因子来控制速度的权值,以减少搜索过程中的盲目性,提高收敛速度。

然而,上述研究均未考虑双凸透镜缺陷工业检测的实时性需求,没有对运行时间和精度提升进行综合性优化。综上,本课题提出了一种基于最大类间方差法的双阈值图像分割算法,使用改进粒子群算法对最大类间方差法进行优化。

1 双凸透镜缺陷检测预处理

由于双凸透镜的反射折射特性,本课题的样本选用低角度环形光源进行打光,检测系统选用CMOS面阵相机(大恒图像公司的MER-630-60U3C相机)采集双凸透镜图像。透镜中除主要缺陷目标外还有其他噪声干扰,会产生少量峰值,这些信息对缺陷提取会造成较大影响,因此需要对采集图像进行预处理,选用合适滤波方案和ROI(region of interest)提取方案剔除这些无关信息。

1.1 图像滤波

图像滤波是常见的消除噪声方式,包括频率域滤波和空间域滤波[11]。频率域滤波算法复杂、计算速度慢;而空间域滤波应用模板卷积对图像的每个像素进行局部处理,算法简单,处理速度快。为满足实时性需求,本研究对图像的去噪考虑采用空间域滤波的方式进行预处理。常见的去噪滤波主要有线性滤波和非线性滤波两种,比如高斯和均值滤波属于线性滤波,而中值和双边滤波则属于非线性滤波。

本课题通过高斯滤波、双边滤波、中值滤波和均值滤波分别对带有缺陷的灰度原始图像进行滤波处理。由于缺陷占原始图像比例较小,为了更清晰地展现滤波效果,截取了100×100像素大小的局部缺陷,观察实验结果,如图1～图4所示。图1为粗划痕缺陷原始图及用4种滤波方法处理后的对比图;图2为强麻点缺陷原始图及用4种滤波方法处理后的对比图;图3为细划痕缺陷原始图及用4种滤波方法处理后的对比图;图4为弱麻点缺陷原始图及用4种滤波方法处理后的对比图。

图1 粗划痕图像滤波对比图Fig.1 Coarse scratch image filtering comparison

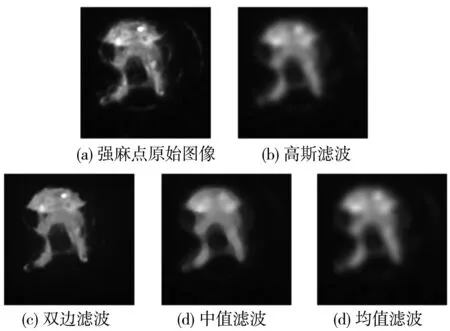
图2 强麻点图像滤波对比图Fig.2 Strong pockmark image filtering comparison

图3 细划痕图像滤波对比图Fig.3 Fine scratch image filtering comparison

图4 弱麻点图像滤波对比图Fig.4 Weak pockmark image filtering comparison

从图1～图4可见,高斯滤波处理后仍然含有少量的噪声,但划痕缺陷细节丢失的较少;中值滤波和均值滤波处理有效去除了不必要的脉冲噪声,但缺陷细节信息丢失得较为严重;双边滤波不仅较好保留了光学镜片划痕缺陷的细节,而且有效去除了噪声,视觉上处理效果最佳。

为了更客观地评价不同滤波算法的去噪效果和关键信息的保留程度,引入均方误差(MSE)和峰值信噪比(PSNR)作为评价指标[12]。MSE值越小,PSNR值越大,则说明滤波降噪之后的图像更加接近原图像,降噪效果更好。如式(1)和式(2)所示:

(1)

(2)

式(1)中,f(i,j)表示图像在像素点(i,j)处的灰度值;g(i,j)表示滤波处理后的图像在像素(i,j)处的灰度值;h×w表示图像的大小。式(2)中,n表示每个像素的比特数。

通过对图1～图4的4种缺陷原始图像处理后的滤波效果图进行分析,得出PSNR评价指标,如表1所示。

从表1可知,4种缺陷原始图像在双边滤波处理后,比高斯滤波、中值滤波和均值滤波处理后的PSNR值更高。说明经过双边滤波平滑处理后的图像更接近原图像,降噪效果更好。通过直观观察和评价指标综合得出,双边滤波处理效果优于其他滤波,因此本课题用双边滤波对双凸透镜缺陷图像进行滤波处理。

1.2 感兴趣区域提取

本课题主要研究目标是双凸透镜内的缺陷检测,透镜外的部分需要剔除,以减少无关信息的干扰。因透镜外轮廓呈圆形,故圆形的检测是提取透镜主体的关键步骤。常用的圆检测方法[13]有霍夫圆变换、最小二乘法拟合圆等,其中应用比较广泛的是霍夫圆变换。本课题采用OpenCV库中的HoughCircles()函数,对透镜图像外轮廓进行提取,再对原图内部构造圆形掩膜,对掩膜部分提取出透镜区域,关键步骤如图5所示。

图5 感兴趣区域提取图Fig.5 Region of interest extraction

2 粒子群算法优化Otsu

2.1 Otsu算法

Otsu算法把图像分割为目标和背景两个区域,通过计算两个区域的方差值大小进行对比,方差值越大,说明目标和背景两区域的差异越大,使得方差值最大的灰度值被认为是最佳的分割阈值。

设H=(0,1,2,…,L-1)为灰度图像的L个不同的灰度值,ni表示灰度值为i(i∈H)的像素数,总的像素数为:

(3)

灰度值为i的像素点在整幅图像所占比例为pi,pi计算公式为:

(4)

因此得出:

(5)

实际上,Otsu算法可以扩展到任意数量的阈值,本研究考虑将图像分割成3部分,因此需要两个阈值k1和k2将灰度图像分割成3个区域,其中灰度值范围在[0,k1]的像素点归为C1类,灰度值范围在[k1+1,k2]的像素点归为C2类,灰度值范围在[k2+1,L-1]的像素点归为C3类,则3类区域的概率分别为P1、P2、P3,计算公式为:

(6)

3类区域的概率满足式(7):

P1+P2+P3=1

(7)

求得3类的平均灰度值分别为μ1、μ2、μ3,计算公式为:

(8)

得出灰度图像的整体平均灰度为μH,计算公式为:

μH=P1μ1+P2μ2+P2μ2

(9)

根据以上公式可以求出C1、C2、C3之间的类间方差σ2的值:

σ2=P1(μ1-μH)2+P2(μ2-μH)2+P3(μ3-μH)2

(10)

对于比较简单的灰度图像,Otsu单阈值的分割效果比较理想;而对于较为复杂的图像,则需要将Otsu推广到多阈值来改善分割效果。由于Otsu算法是通过遍历所有灰度级来求取最佳分割阈值的,因此计算量很大,难以满足实时处理的要求。

2.2 粒子群优化算法

PSO算法首先生成一组随机的粒子群x=(xi1,xi2,…,xiD),i=1,2,…,N。其中,N代表种群规模的大小,D代表粒子的维度空间。

粒子的速度更新公式是由记忆项、自身认知项、群体认知项组成的。权重大小和粒子的当前速度矢量构成了记忆项。当前指向粒子自身最好的矢量构成了自身认知项,体现了粒子的搜索行动含有自身经验的部分。粒子当前指向群体中最优的矢量构成了群体认知项,体现了粒子之间的合作共享。粒子搜索就是通过将自己的经验和同伴中最好的经验综合考虑,来决定下一步如何行动。每个粒子的搜索距离大小和方向选择是由粒子的速度矢量决定的,粒子的速度更新如式(11)所示:

vi,j(t+1)=wvi,j(t)+c1rand1(pbestij(t)-

xij(t))+c2rand2(gbestj(t)-xij(t))

(11)

其中,j∈{1,2,…,D},xij(t)表示维度为j的粒子xi在第t次的迭代位置,vij(t)表示维度为j的粒子xi在第t次的迭代速度,pbestij(t)表示维度为j的粒子xi在之前t次迭代中最优的个体位置,gbestj(t)表示整个粒子种群在之前t次迭代中最优的位置,c1和c2代表着学习因子,一般设定为2,w表示惯性权重,rand1和rand2是在[0,1]上随机分布的数值。当粒子速度更新完成之后,粒子的位置也相应更新。粒子位置更新由当前位置和当前速度向量构成,如式(12)所示:

xij(t+1)=xij(t)+vij(t+1)

(12)

根据式(11)(12)即可得出如图6所示的粒子位置和速度更新示意图。

图6 位置和速度更新示意图Fig.6 Location and speed updates

图6中,3条虚线方向代表着影响粒子迭代后位置的前提因素,分别是粒子当前速度、当前粒子最优值和全局粒子最优值。3条实线代表着记忆项、自身认知项和群体认知项。点划线则代表着粒子更新后的速度,决定了粒子更新后的位置。

假设优化问题是最大值问题,若当前时刻粒子的目标函数值比其历史最优值还大,则用当前的目标值对应的位置替换其历史最优位置,pbesti(t+1)更新方式如式(13)所示:

(13)

其中,f是目标函数。

假如当前粒子的历史最优值比全局最优值更大,则用当前粒子的历史最优值对应的位置替换其全局最优位置,gbest(t+1)更新方式如式(14)所示。

(14)

3 改进粒子群优化Otsu

3.1 改进的粒子群优化算法

关于惯性权重w的更新策略中,线性递减更新策略的应用最为广泛[14]。但线性递减更新策略在迭代初期阶段容易搜索不到最优值范围,从而在后期易陷入局部最优。为增强粒子前期全局搜索能力,提升后期局部收敛速度,式(11)中记忆项部分的w权重选择非线性递减函数,如式(15)所示:

(15)

其中,t为当前迭代次数,T为最大迭代次数,为了让粒子在初期迭代阶段有较大权重,后期让粒子减小权重wmin取0.4,wmax取0.9。

为减少搜索过程中的盲目性,提高收敛速度,在位置更新式(12)中引入约束因子α来实现控制速度的权值。

xij(t+1)=xij(t)+αvij(t+1)

(16)

α=0.1+w

(17)

传统粒子群优化算法中的约束因子为1。α引导粒子在最佳位置附近盘旋,α的改进控制了速度对位置的影响,从而更好地提高了算法的收敛性。

当粒子陷入局部最优时,为跳出局部最优,应当加入新的粒子群进行扰动,这也导致种群规模扩大,从而增加了计算量。因此提出一种新的策略来更新粒子群,在保持粒子群总数不变的同时,提高粒子的多样性,并提高收敛速度。具体策略为:当全局最优值保持一定迭代次数不变时,通过式(11)和(12)随机产生一定数量的粒子,假设为W个,其中初始总粒子群数量为N个。随机产生的W个粒子与N个原始粒子相加得到W+N个粒子,根据目标函数值对其进行从大到小重新排序。为了保持总粒子群数量不变,保留前N个粒子,剔除后W个粒子,使得粒子跳出局部最优,从而寻得全局最优。根据式(14)判断当粒子的历史最优值大于全局最优值,替换了全局最优位置之后,将该粒子的位置参数和速度参数进行重新随机分布,激活该粒子的全局搜索能力,以防止该粒子陷入局部最优解,丢失寻优能力。

3.2 改进粒子群优化算法的Otsu图像双阈值分割算法步骤

改进粒子群优化算法的框架流程如图7。

图7 算法框架流程图Fig.7 Algorithm framework flow chart

4 实验结果及分析

为了验证改进粒子群优化算法的Otsu图像双阈值分割效果,分别对划痕和麻点两张含有缺陷的图像进行处理,图像的尺寸为1 200×1 200像素。算法在Windows10、2.30 GHz处理器、16 GB内存上处理;编程环境为Visual Studio 2022,并且采用OpenCV库对透镜进行处理。参数设定为:粒子数目N为30,vmin=-10,vmax=10,c1=c2=2,wmin=0.4,wmax=0.9,最大迭代次数T=200,W为0.1 T,维度空间D=2。分别采用自适应算法、最大熵算法、一维Otsu单阈值算法、二维Otsu单阈值算法、双阈值Otsu算法、PSO+Otsu算法、改进PSO+Otsu算法对划痕和麻点缺陷透镜进分割,局部放大缺陷位置后,图像尺寸为100×100像素的分割效果如图8和图9所示。

图8 划痕图像阈值分割Fig.8 Scratch image threshold segmentation

图9 麻点图像阈值分割Fig.9 Pockmark image threshold segmentation

由图8可见,自适应存在部分缺陷丢失的情况,最大熵、一维Otsu和二维Otsu存在缺陷不连续、断连的情况,没有将划痕缺陷较好地分割出来,而双阈值Otsu、PSO+Otsu和改进PSO+Otsu能够较为完整地提取出缺陷区域,分割得比较完整。由图9可见,麻点图像阈值分割效果图中自适应存在缺陷边界不明确的问题,最大熵、一维Otsu和二维Otsu存在缺陷断连,且麻点内部出现空隙等问题,没有较为完整地提取出麻点缺陷,而双阈值Otsu、PSO+Otsu和改进PSO+Otsu能够较为完整地提取出整体的缺陷部分。但改进PSO+Otsu算法和双阈值Otsu、PSO+Otsu算法在处理时间上有所区别,本研究针对划痕和麻点两张缺陷图像,选取一维Otsu、双阈值Otsu、PSO+Otsu和改进PSO+Otsu进行对比,每个算法均运行30次,并且针对运行时间、最佳阈值、最优迭代次数和适应度值,在去除最高值和最低值后,对数据进行取平均值处理,具体结果如表2所示。

表2 透镜缺陷平均实验结果表Tab.2 Average experimental results of lens defects

分析表2可知,一维Otsu算法虽然平均处理时间较短,但是只有单个阈值,分割效果差。双阈值Otsu算法在处理划痕图片时,需要遍历所有灰度级来得到最佳分割阈值,虽然能获取最优的适应度值,从而寻找到最优的两个阈值,但是计算量大,导致运行时间长。通过数据得出改进PSO+Otsu比双阈值Otsu的运行时间节省约52.7%。PSO+Otsu虽然结合了粒子群的优势,但寻得最优解所需的迭代次数更多。通过数据得出改进PSO+Otsu比PSO+Otsu在运行时间上节省约32.3%的时间,并且在寻得最优适应度值时存在误差,说明有个别实验中粒子群有陷入局部最优的情况出现,且无法跳出局部最优。

PSO+Otsu和改进PSO+Otsu收敛速度的差距如图10、11所示。从图10、11可知,改进PSO+Otsu算法在前期能较快的收敛至目标适应度值,且当适应度值保持一段时间不变时,也就是粒子陷入局部最优时跳出局部最优的能力也优于PSO+Otsu算法。

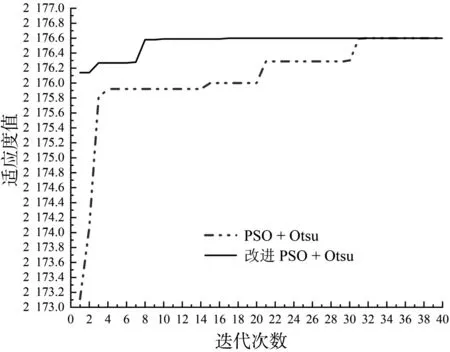
图10 划痕迭代收敛图Fig.10 Scratch iterative convergence

图11 麻点迭代收敛图Fig.11 Pockmark iterative convergence

5 结论

为解决双凸透镜实时缺陷检测中图像阈值分割存在的精度不高,检测速度慢的问题,本研究以双凸透镜的划痕和麻点作为研究对象,提出一种基于改进粒子群算法优化Otsu阈值分割的方法。在标准PSO+Otsu的基础上,引入一种改进的PSO优化算法,对粒子多样性和失去活性方面进行优化。通过对含有划痕和麻点的缺陷图像进行多实验和多算法的检测。实验证明该优化算法在分割精度上均优于自适应、最大熵、一维Otsu、二维Otsu和PSO+Otsu分割算法。在检测速度上均快于双阈值Otsu和PSO+Otsu算法。实验数据显示该优化算法能有效提升双凸透镜缺陷检测的检测速度和精度。

由于本研究仅针对Otsu分割算法进行粒子群优化,没有多角度分析粒子群优化对传统分割算法的性能提升,如何拓展优化算法至其他分割算法是未来的工作重点。