基于SSA算法优化SVM的发动机润滑油信息状态评估*

李英顺 张国莹 张 杨 贺 喆 周 通 左 洋

(1.北京石油化工学院信息工程学院 北京 102617；2.沈阳顺义科技有限公司 辽宁沈阳 110000； 3.陆军装备部驻沈阳地区军事代表局驻沈阳第三军事代表室 辽宁沈阳 110000)

发动机是步履装甲车辆的核心部件[1]，其健康状态直接影响装甲车辆的正常运行。润滑油的理化信息和磨粒信息能够及时反映发动机健康状态，通过传感器测量润滑油的这两种信息，可为装甲车辆发动机的换油以及维修提供依据。FAN等[2]利用磨粒运动特征差异研究了颗粒速度与颗粒直径和油液黏度的关系，为发动机润滑油智能监测提供了新思路。吕克洪[3]利用铁谱技术与图像识别技术，对动力系统进行故障诊断研究，实现了对动力系统的检测与诊断。但上述研究仅使用单一磨粒信息或单一的理化性能对设备进行状态评估，评估结果缺乏全面性和准确性。

支持向量机(Support Vector Machine,SVM)可以较好解决样本数量有限情况下寻找最优解的问题，但其分类性能受自身参数影响较大。JOHN等[4]使用网格搜索优化SVM参数，提高了分类性能，但由于搜索步长较为宽泛而导致寻优时间较长。LUO等[5]使用量子粒子群(Quantum Particle Swarm Optimization,QPSO)优化SVM参数，提高了全局搜索能力，但此方法容易出现早熟收敛、局部寻优能力变差的问题。

麻雀搜索算法(Sparrow Search Algorithm,SSA)是一种新型的种群优化算法[6]，其在搜索精度、收敛速度、稳定性和避免局部最优值方面都要比现有算法表现更佳。因此，本文作者利用SSA优化SVM的惩罚因子和核参数，选取最优参数建立SSA优化SVM的评估模型，并对发动机润滑油数据进行训练和验证。

1 算法设计

1.1 麻雀搜索算法

麻雀搜索算法是一种新型的以麻雀种群寻找食物和反捕食行为为依据的优化算法。麻雀群体中包括发现者、加入者和警戒者。

设由n只麻雀组成的种群X为

(1)

式中：d为需要优化的问题的维数。

在种群中所有麻雀的适应度值Fx为

(2)

式中：f为适应度值。

在SSA模型中，正常情况下，在食物搜索过程中，具有优先获取食品权利的往往都是适应度值更优的发现者，且发现者的位置在每次迭代后更新。其位置更新函数为

(3)

式中：t为过程中需要迭代的次数；Nmax为迭代过程中的最大次数；Xi,j是第i只麻雀在第j个维度中的位置；α为随机的数字，且α∈(0,1]；R2为预警值；RS为安全值，且R2∈[0,1]，RS∈[0.5,1]；Q为随机的数字，并且该随机数服从正态分布；L是一个1×d的矩阵，L矩阵内的每个元素都是1。

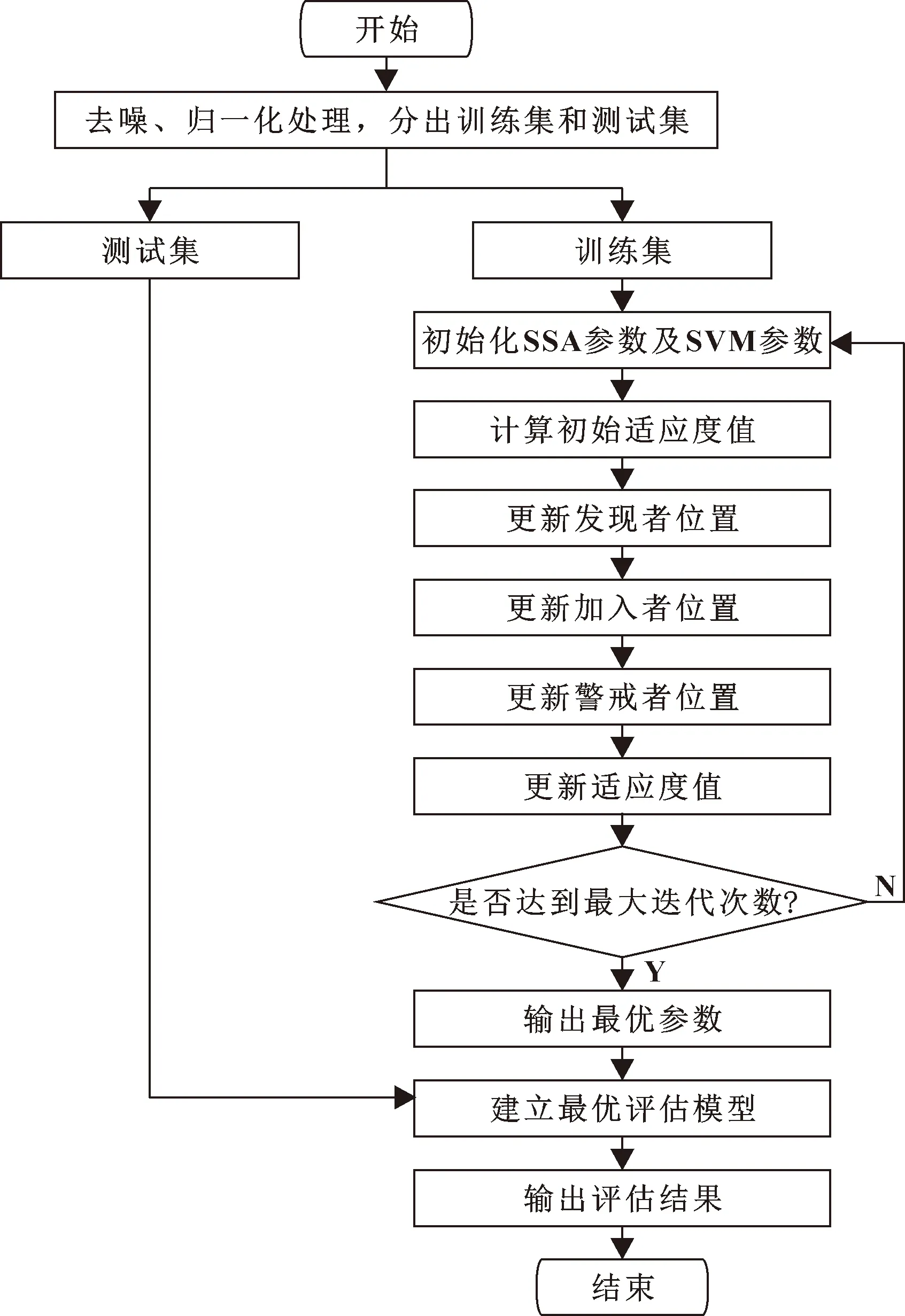
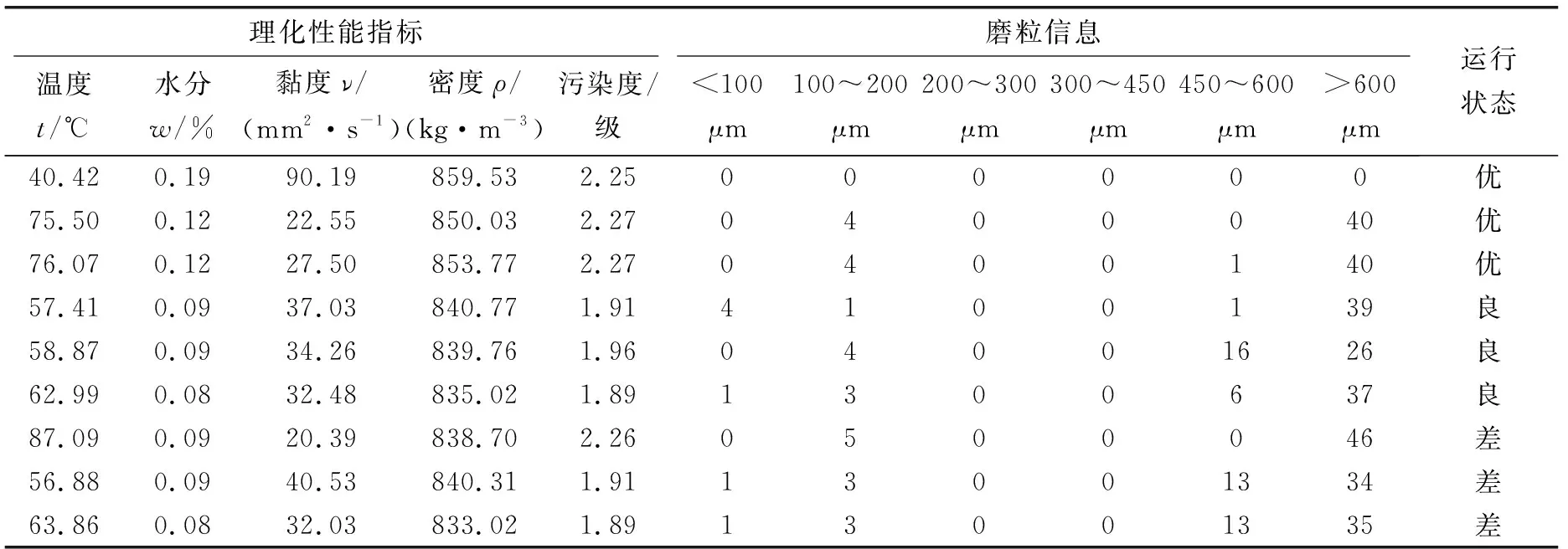
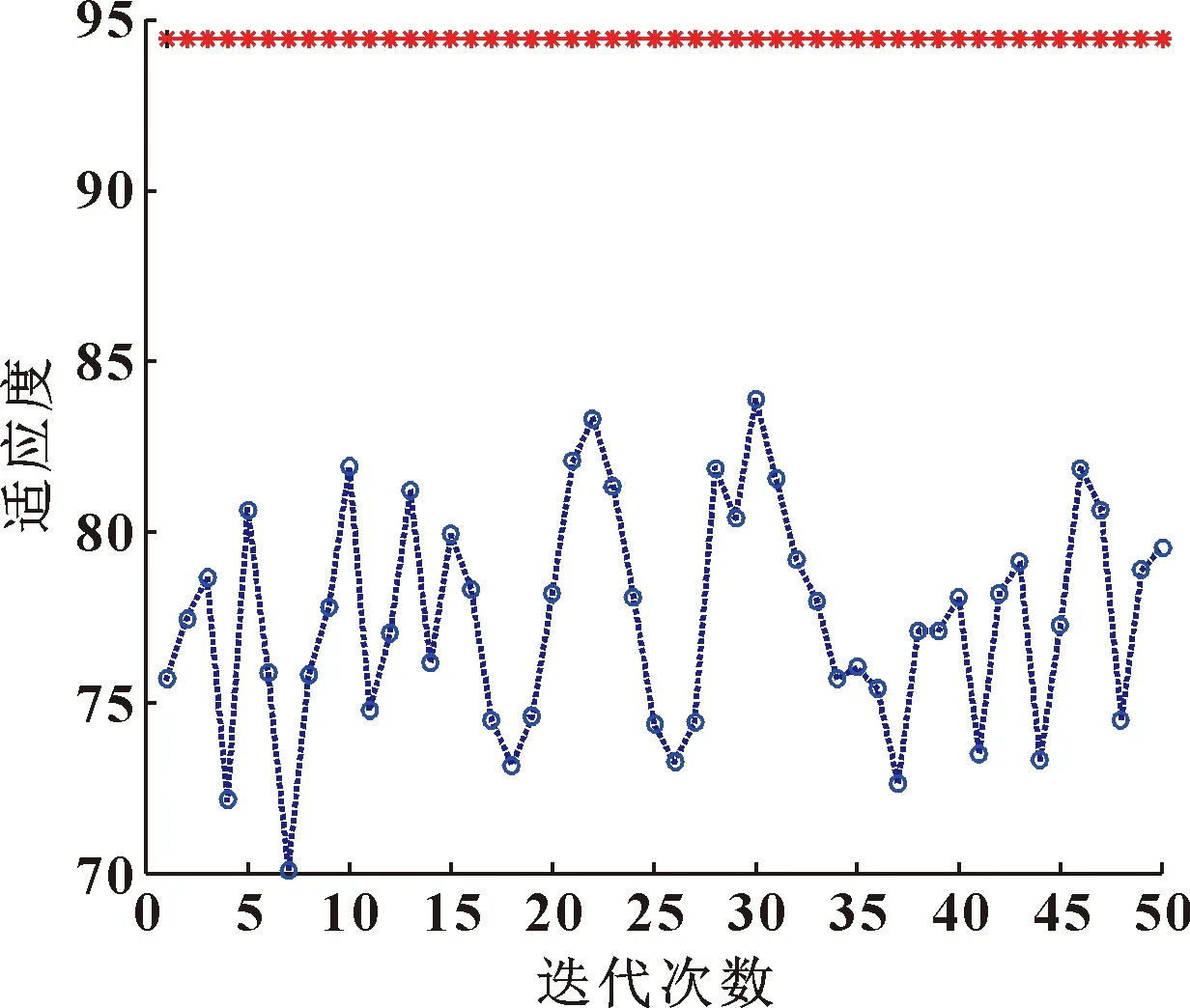
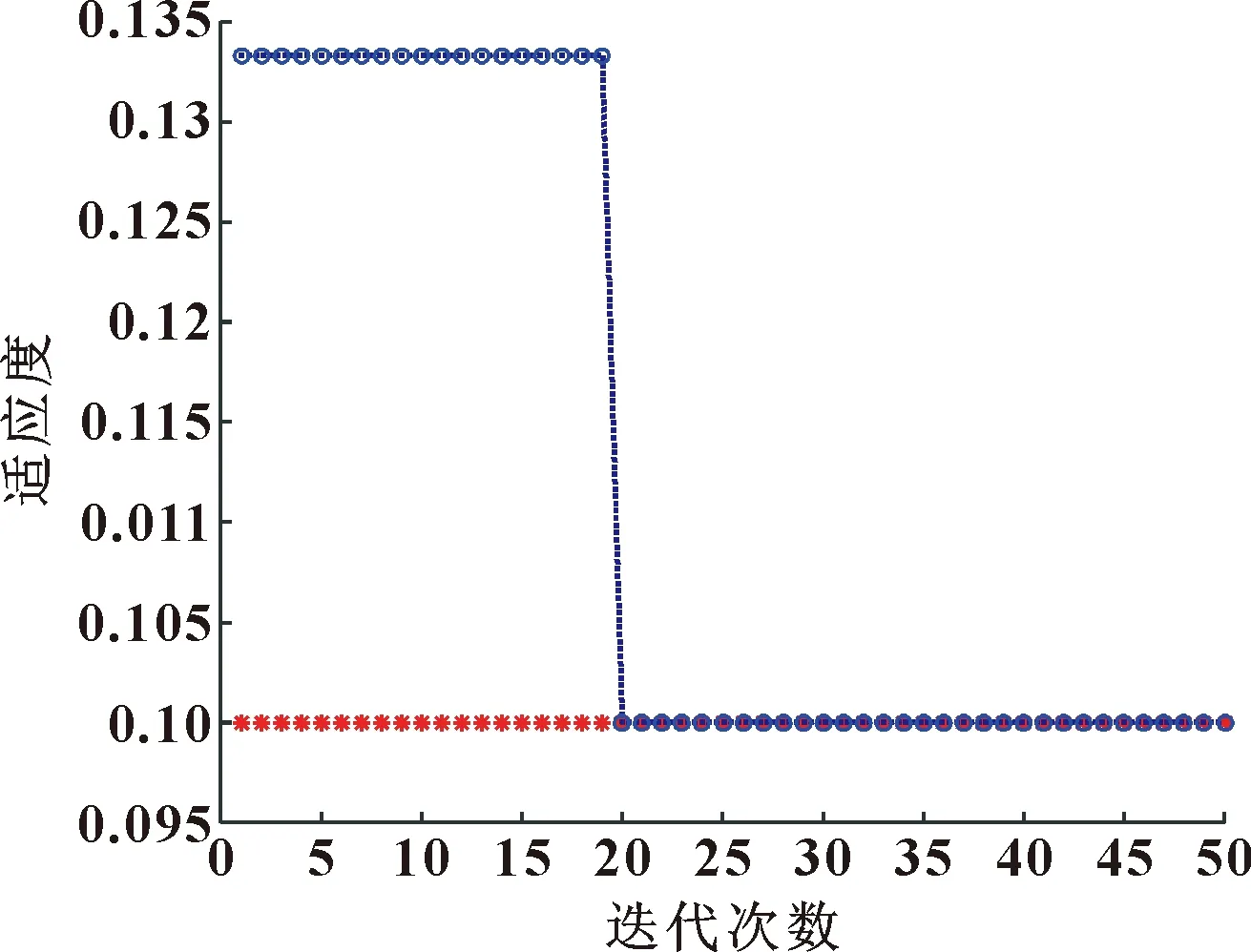
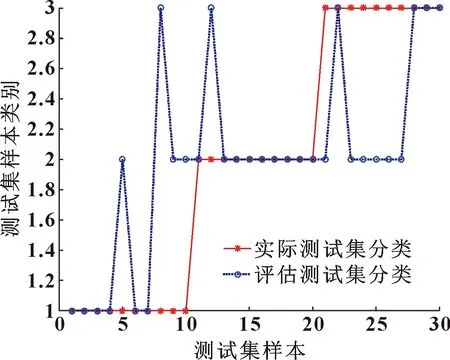
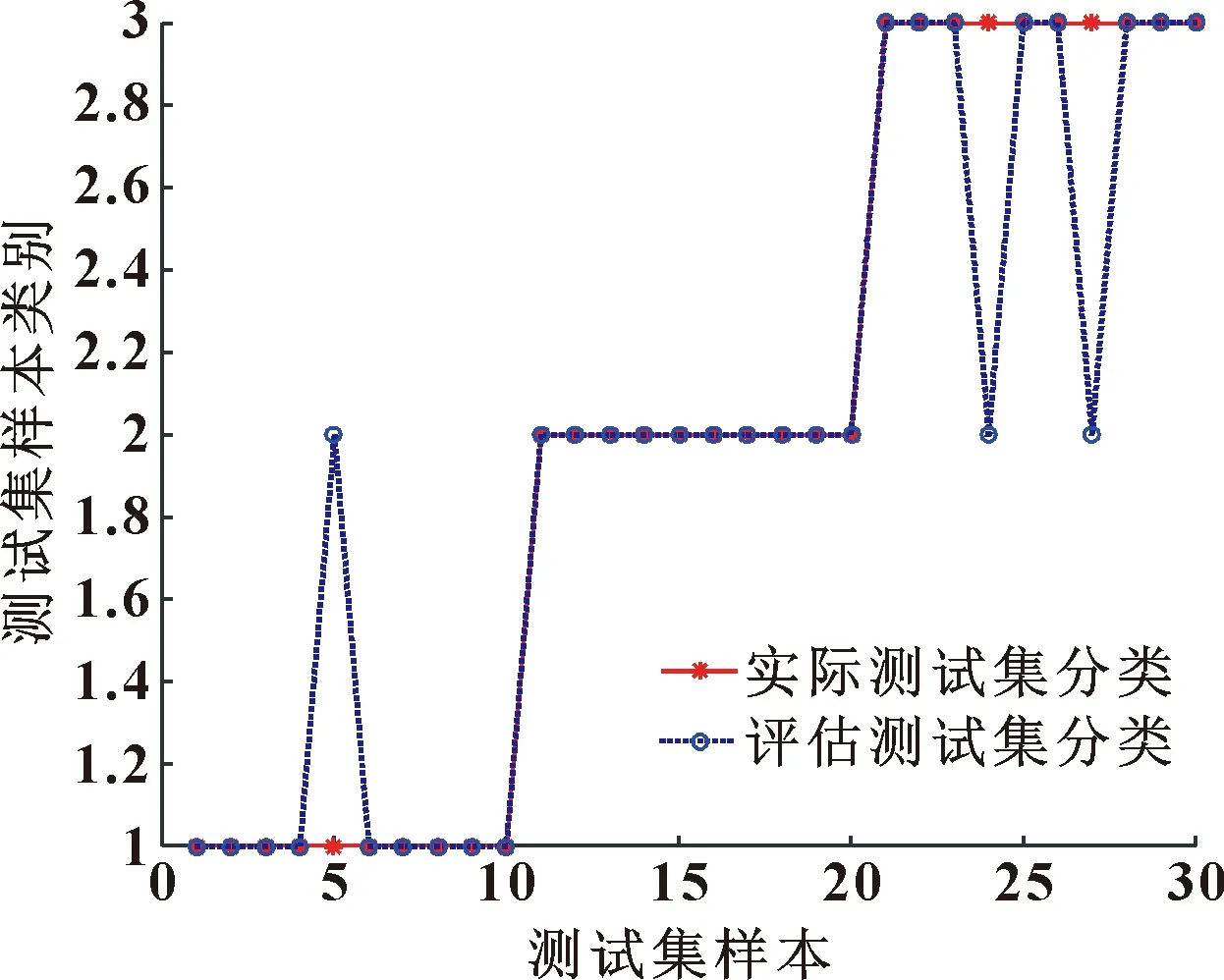
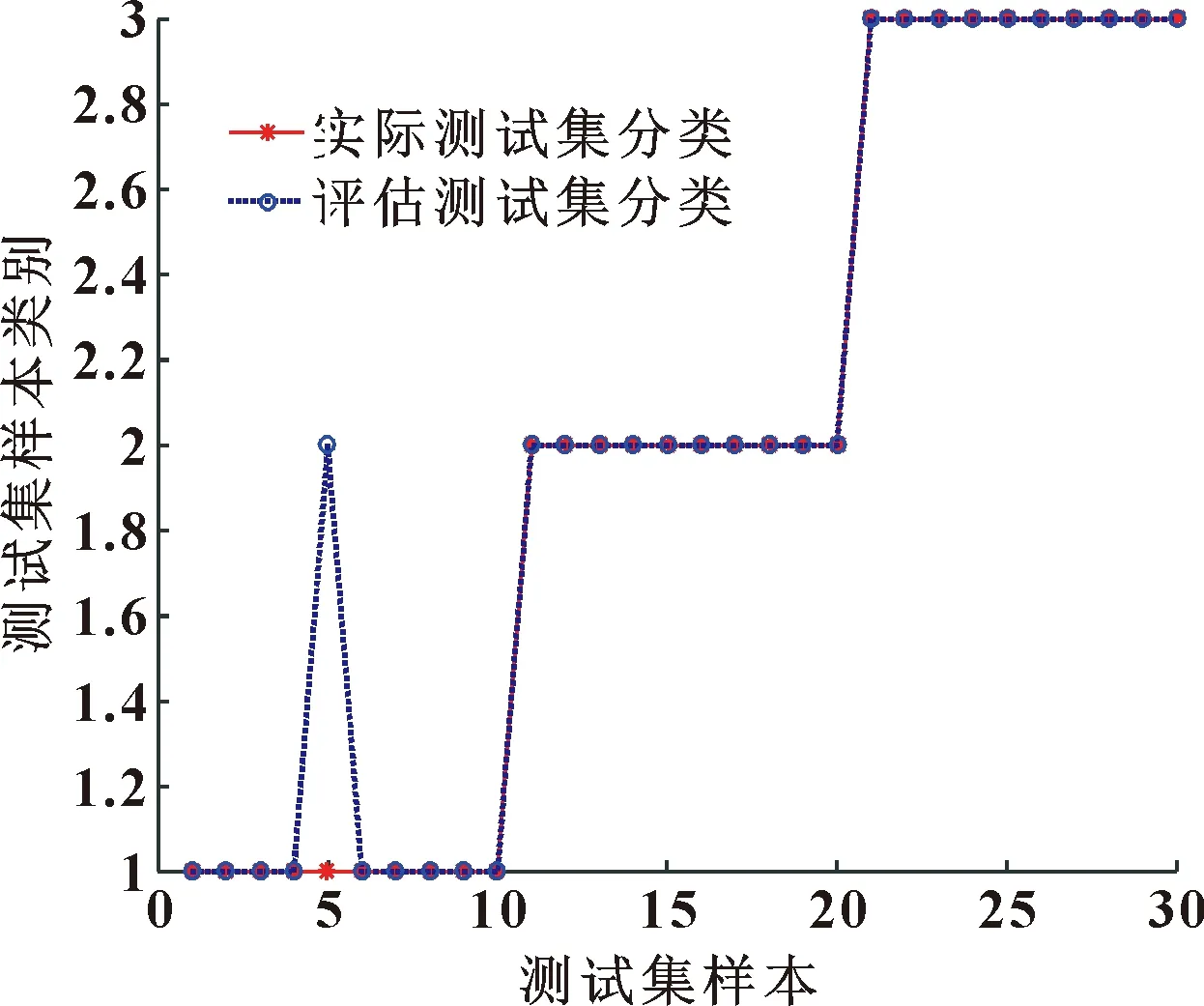
当R2

在整个觅食过程中，发现者的行动轨迹会一直被加入者监视。加入者一旦察觉到种群里的发现者获得了新的食物来源，它们就会很快离开现在的位置去新的位置争抢食物。在这个过程中，如若它们赢了，它们就可以立即获得该发现者的食物，否则它们就需去其他位置重新寻找食物。加入者的位置会重新更新，如式(4)所示：

(4)

式中：XP为当前发现者的最优位置；Xworst为全局当中最差的位置；A是一个1×d的行矩阵，该矩阵A中的每一个元素不是1就是-1，并且A+=AT(AAT)-1；当i>n/2时，适应度值比较低的第i个加入者，没有占领到食物，需要飞到别的位置寻找食物。

在模拟实验中，假设种群中的警戒者数量占种群中麻雀总数量的10%～20%，并且它们的初始位置是在种群中随机产生的。当种群遇到危险时，处于边缘位置的麻雀将会向中间的安全位置移动，以获取更好的位置。警戒者位置更新表示如下：

(5)

式中：Xbest是当前情况下全局的最优位置；β是步长的控制参数；K是随机的数字，且K∈[-1,1]；fi是麻雀个体在种群中的适应度值；fg和fw分别是全局最佳适应度值和全局最差适应度值；为避免分母出现0的情况，设置了常数ε。

当fi>fg时，表示此时的麻雀正处于种群的边缘，非常容易遭到捕食者的攻击。Kbest这个位置是种群中最好且最安全的位置。当fi=fg时，表示此时处于种群中间的麻雀感知到危险状态的存在，并开始向其他位置的麻雀靠近，从而将被捕食者捕食的风险降到最低。K是麻雀移动的方向，同时也是步长控制参数。

1.2 支持向量机算法原理

1963年，苏联学者Vapnik和Lerner研究发现了由模式识别发展而来的分类器——SVM理论[7-8]，并在20世纪七八十年代成为统计学的一部分。SVM优化不仅考虑了要将经验风险达到最小化，还考虑了将结构风险达到最小化，使得分类具有更好的稳定性；SVM具有良好的泛化能力，可以在样本数据数量比较少的情况下寻求到最优解。SVM可以很好地解决像发动机这样运行状态样本不容易获取的分类识别问题。SVM的基本思想是：在样本空间或特征空间中求解出一个与各类别样本之间距离最大的平面，这个平面被叫做最优超平面[9-10]。

为了解决部分样本可能会出现不能被SVM正确分类的情况，引入一个松弛变量ξi≥0,i=1,2,3,…,n，约束条件方程式如下：

yi[φ(X)ω+b]-1+ξi≥0

(6)

式中：Xi代表样本；yi代表其对应类别。

同时引入一个惩罚因子c用于调节被分错样本的惩罚程度，因此可以通过求式(7)的极小值获取‖ω2‖的最小值。

(7)

对式(7)用拉格朗日法进行求解，同时解出子集样本中非零拉格朗日乘子，并以该样本向量作为支持向量。广义最优超平面是其决策函数的表达式，如式(8)所示：

(8)

式中：αi表示每个样本的拉格朗日乘子，且αi≥0。

对于SVM理论中非线性可分样本问题，可以分为以下两步操作：

(1)将非线性待分类样本映射到高维空间中，使非线性可分变为线性可分；

(2)在原空间函数下，完成训练样本之间高维空间的内积运算。

该原空间函数是一种非线性映射函数，被称为核函数[11]。该函数的选取要满足Mercer条件[12]，其对应某一空间的非线性变换φ(X)，该核函数表示为

K(Xi,X)=φ(Xi)φ(X)

(9)

引入核函数之后，非线性样本的SVM决策函数为

(10)

根据不同的非线性可分数据选取合适的核函数，文中综合发动机润滑油信息数据特点，选取径向基核函数作为SVM理论的核函数。

径向基核函数RBF:

K(Xi,X)=exp{-g‖Xi-X‖2}

(11)

从式(11)可以看出，需要对支持向量机的核参数g和惩罚参数c进行优化[13-15]。选用较好的优化算法优化这两个参数，以达到更好的SVM分类效果，进行准确的状态评估。

2 评估模型建立

麻雀所搜算法相比于其他优化算法，具有搜索精度高、参数设置少、收敛速度快的优点，利用SSA对核参数g和惩罚参数c进行优化，从而避免模型在寻优过程中出现局部最优、收敛速度慢和搜索精度低的问题，达到更好的分类效果。

建立基于SSA优化SVM的发动机状态评估模型流程如图1所示。

图1 SSA优化SVM的发动机状态评估模型计算流程Fig.1 Calculation flow of engine condition evaluation model based on SVM optimized by SSA

SSA算法优化SVM相关参数步骤如下:

(1)首先确定状态评估模型的输入和输出，将油液信息的特征值作为模型的输入，发动机运行状态作为目标输出。对获取的发动机润滑油信息数据进行归一化处理，建立相应的训练集和测试集。

(2)初始化SVM及SSA的相关参数，其中包括SVM的惩罚参数c和核参数g，以及SSA算法中的种群规模、迭代次数等。

(3)通过SVM的交叉验证对训练集进行分类，以交叉验证的准确率作为麻雀个体的适应度值，并保留最佳的适应度值及最优位置信息。

(4)随机给定预警值，并将预警值与安全值进行比较，根据式(3)对发现者位置进行更新。

(5)根据式(4)对加入者位置进行更新。

(6)根据式(5)对警戒者位置进行更新。

(7)完成种群位置更新后，计算麻雀新位置的适应度值，将更新后的适应度值与原最佳适应度值进比较，并更新全局最优位置信息。

(8)最终判断是否达到最大迭代次数，若未达到重复执行步骤(3)，若满足条件则终止循环，输出最优参数，并根据最优参数建立最优评估模型。

(9)将测试集输入评估模型，输出评估结果，结束运行。

3 实例验证

以某型装甲车辆发动机为研究对象，对发动机润滑油信息的120组数据进行预处理，并按照运行状态将其分为“优”、“良”、“差”3个评价等级，每组状态分别选取40组数据，其中30组作为训练集，10组作为测试集。部分数据如表1所示。

表1 部分发动机润滑油数据Table 1 Some engine lubricating oil data

首先，对初始数据分别进行整体和分维可视化处理，并绘制出润滑油数据分维可视化图，如图2所示。

图2 分维可视化图Fig.2 Fractal visualization

将原始数据进行归一化处理，并使用网络训练SVM、QPSO-SVM、SSA-SVM,根据润滑油信息数据对发动机运行状态进行分类识别，设置最大迭代次数为50次。QPSO和SSA分别对SVM的核参数g和惩罚参数c进行优化，优化算法的迭代寻优曲线如图3、图4所示。

图3 QPSO-SVM寻优曲线Fig.3 QPSO-SVM optimization curve

图4 SSA-SVM寻优曲线Fig.4 SSA-SVM optimization curve

经对比，文中选用的SSA算法优化SVM准确率最高，可达到96.67%。网格搜索法耗时较长，搜索步长宽泛，参数不准确；QPSO算法收敛速度慢，且局部寻优能力差，SSA-SVM算法具有更强的寻优能力，收敛速度更快，能够快速准确地寻找到最优参数。3种分类方法的诊断模型与预测分类结果如图5—7所示。

图5 SVM实际测试集与预测测试集分类结果Fig.5 Classification results of SVM actual test set and predictive test set

图6 QPSO-SVM实际测试集与预测测试集分类结果Fig.6 Classification results of QPSO-SVM actual test set and predicted test set

图7 SSA-SVM实际测试集与预测测试集分类结果Fig.7 Classification results of SSA-SVM actual test set and predicted test set

根据3种方法状态分类的模型对分类结果进行对比，如表2所示。

表2 分类结果对比Table 2 Comparison of classification results

从表2可看出： SSA优化的SVM运行时间最短为1.48 s，准确率最高为96.67%。经过SSA优化的SVM对装甲车辆发动机状态评估具有更优的分类效果。

4 结论

采用优化支持向量机评估模型，根据装甲车辆发动机获取的润滑油信息对装甲车辆发动机进行状态评估，通过MATLAB仿真后能够根据润滑油数据对发动机运行状态进行较为准确的评估，该模型评估准确率为96.67%，运行时间为1.48 s，相比于普通SVM模型以及QPSO-SVM模型在评估准确率及运行时间上有明显的优势。文中提出的状态评估方法能为装甲车辆发动机状态评估提供科学依据，并且能够给维修保障人员提供技术支持。