基于伽马内核与加权K近邻的流量分类算法

徐 魁，海 洋，许艺凡，段靖海，孙炜策，陶 军

(1.宝鸡市公安局通信处，陕西 宝鸡 721014;2.东南大学 网络空间安全学院，江苏 南京 211189;3.计算机网络和信息集成教育部重点实验室(东南大学)，江苏 南京 211189)

0 引 言

网络安全逐渐成为当今信息化社会的焦点问题，目前网络上存在的攻击种类相当多，例如拒绝服务攻击、端口扫描以及Web木马等等。异常流量的分类成为防护环节中必不可少的一环。除了传统基于端口和载荷的流量分类，将机器学习应用至网络流量的分类[1]也越来越多。相关的机器学习算法包括了聚类算法、KNN算法、决策树、随机森林和深度神经网络等[2]。其中，在分类问题中，KNN算法简单而高效。

对于各种分类问题的改进，主要体现在权重函数改良、距离函数的设计等方向；而数据集不均衡问题的处理方式最常见的是过采样和降采样，让数据集分布变得均衡，但通过加权的方式也能够抑制数据集不均衡带来的问题。

在权重设计方面，H. Yigit等[3]提出用人工蜂群算法找到KNN的最佳权重，从而实现更好的分类效果；Su等人[4]提出使用遗传算法来计算最佳权重，同时用聚类中心代替部分训练数据集，缩短执行时间；毕等人[5]提出了一种基于高斯函数定权的KNN算法，应用在室内定位问题上，提高了定位准确率和鲁棒性。

而在距离函数的处理上，Juan Aguilera等人[6]提出了用基于牛顿引力公式进行加权；Zhang等人[7]提出了基于随机森林的加权特征，考虑了每个特征的差异性；但两者都没有考虑数据集不均衡问题。杨等人[8]提出了一种基于语义距离的KNN算法，分析属性内取值的语义差异，尤其在数据集不完整的情况下，分类准确率优于传统方法。

在函数设计方面，Lin等人[9]提出了Focal Loss的概念，在原有的交叉熵损失函数上做了进一步修改，使得模型更加关注于小样本的部分，进一步提高了网络分类的准确率，这一修改思路也可以在KNN分类中借鉴；周等人[10]提出了一种基于聚类改进的KNN分类算法，先聚类再分类，提升了KNN算法的效率；韦等人[11]提出了一种基于改进极端随机树的方法，通过对加权统计和修改投票规则，其模型在异常流量样本较少的类别上分类效果较好。

对于数据集不均衡问题，Liu等人[12]提出了类置信权重，依据每类标签属性值的概率对KNN进行加权，对于不平衡的数据集，其分类效果有一定的改善；Cao等人[13]为每个样本分配反比例权重然后与距离权重结合，这是一种简单的距离加权；Ying等人[14]在异常日志分类中用到了大量数据挖掘和自然语言处理的方法，使数据集不平衡问题得到改善。

Zhao等人[15]提出了一种加权混合集成方法，在Boosting框架下，为每个基分类器分配权重，实现对不平衡数据集的有效分类；Li等人[16]提出了一种融合的等比例抽样方法，对少数类进行了更多的关注，提升了分类的准确率；王等人[17]提出了一种SVM和KNN结合的算法，对于较远样本使用SVM分类，对于距离近的样本用支持向量进行KNN分类，提高了少数类样本的识别率。

1 KNN算法

在实际网络环境中，流量往往呈现倾斜式分布，异常流量是少数，数据集一般不均衡，这对于分类结果产生了一定的影响。

原始的KNN根据预测样本周围距离最近的K个点，根据少数服从多数的原则，将这个数据划分为K个数据中出现次数最多的那个类别。

若K的取值较小，分类器很容易受到局部噪声数据的干扰，分类会出现较大偏差；如果K的取值过大，分类器忽略了训练数据中的有效信息，样本更容易被分类到数目多的类别中。而数据集不均衡更容易导致分类准确率下降。

传统的KNN分类存在一定的缺陷，例如，没有充分考虑距离远近对样本权重的影响，距离待测样本近的点，其对分类的结果影响应该更大，应当有更大的权值；同时在数据集分布不均时，KNN总是倾向于将未知测试样本分类为占比数量较多的类，导致占比数量较少的类的分类效果不佳。而在网络流量中，异常流量本身属于少数类别，少数类别的分类准确率对于整个模型分类准确率的贡献也很重要，但传统的KNN不能很好地区分出这些少数异常流量的样本。

而简单的WKNN，为每一个训练样本点给予d的权重，其中d是待测样本与训练样本的距离。这样的方法一定程度上给近距离的点更大的权重，但也使得计算量变大，同时当d趋近于0时，即待测样本和训练样本非常接近时，其权重1/d会趋近于无穷，对应权重值没有上确界。事实上，在高维数据中，计算得到的距离通常都较小，样本之间的差异性更难体现。若这一点为噪声数据，反而会使得分类准确率下降。同时，简单的WKNN也不能缓解数据集分布不均带来的问题。

对于上述提到的两个问题，一个是分类样本对距离的感知所有差别，不同距离的样本，其权重应该要有区分，这是区分样本间的差异性；另一个是对于数据集不均衡的处理，由于KNN总是倾向于将预测样本分类为数量较多的类别，因此需要动态调整权重，这是类别间差异性的体现。

同时，KNN算法属于计算密集型，记训练数据的数量为n，数据的维度为m，则预测一个样本，其时间复杂度T=O(mn)。若在这一阶段进行加权，与一个训练样本每计算一次距离，则至少需要多m次乘法运算，预测一个样本类别至少多出mn次乘法运算。而KNN分类的实质是考虑其周边很少的点，这些点称为关键决策点；对于那些距离很远的点，实则参考性并不大，因此在第二个“投票阶段”进行加权和处理。由于K≪n，因此计算量也会随之减少。

为了解决这些问题，该文提出了一种基于Gamma分布函数的自适应加权KNN模型(G-WKNN)，对于数据集的分布具有一定的自适应性，能够根据样本的差异和类别的差异综合对分类模型进行调整，在提高模型准确率和稳定性的同时，对数量少的类别的分类效果也有提升。在数据不均衡时，类别负载因子起主要调节作用；而在数据较为均衡时，距离感知因子起主要调节作用，从而动态适应数据的变化。

2 基于Gamma分布的自适应WKNN

针对上述提到的问题，该文提出了基于Gamma内核的自适应加权KNN算法，即Gamma-WKNN(G-WKNN)。其中，综合权重w由距离感知权重wd和类别负载权重wf构成。距离感知权重wd反映了决策样本的差异，能够起到不同样本间的调节作用；类别负载权重wf反映了各个类别之间的差异，对于类别不均衡问题，能够起到调节作用。综合权重w的计算方法如式(1)。

w=wdwf

(1)

2.1 距离感知权重wd

记数据集一共有C个类别，样本具有M个属性，在空间Rm中，测试样本P=(x1,x2,…,xm)和训练样本Q=(y1,y2,…,ym)间的闵可夫斯基距离dist可以表示为:

(2)

p取1或者2对应的闵式距离最为常用，这里取p=2，此时的距离为欧几里得距离，得式(3):

(3)

距离感知权重wd，指标应该呈现出随着距离增大，权重降低。同时所选函数应该有上确界，在d很小，甚至趋近于0时，不应该出现无穷大的情况，需要避免1/d这样的函数的缺陷，其衰减应该控制在一个区间范围内；对于常见的高斯内核而言，其可调参数有(μ,σ)，但由于高斯内核的对称性，只能够使用内核函数的一部分区间，同时高斯内核的参数μ只影响曲线在x轴上的偏移，因此可调参数仅有σ。相比之下，Gamma内核的变化较为丰富，更能够适应不同的情况。Gamma内核定义如式(4)所示：

(4)

其中，参数α决定了曲线的形状；而β决定了曲线的陡峭程度，β越大，曲线越陡峭。相比于反比例函数，Gamma分布函数随距离衰减程度可控，可以自由调整；相比于高斯内核，其分布不完全对称，具有一定的扰动，这样的随机性一定程度能够避免受到噪声数据的影响，减少过拟合。

对式(4)x求导，得式(5):

(5)

令Gamma(x|α,β)'=0，得到方程的根，这里考虑α≥1，β>0的情况，得式(6):

(6)

结合一阶导数的在x0处的符号和函数图像，可以判定x0为一个极大值点。将x0带入式(4)，得到Gamma的极大值Gamma(α,β)*，如式(7)所示：

(7)

关于参数α,β对函数峰值的影响，Gamma(α,β)*函数是关于(α,β)的单调函数，关于β单调递增，关于α单调递减。即，若希望函数峰值较大，可以选择较小的α和较大的β。

当α>1，β>0时，可以得到Gamma分布函数导数的递推公式，如式(8)所示：

(8)

根据递推关系式(8)，可求得二阶导数，如式(9)所示：

Gamma(x|α,β)''=

(9)

令Gamma(x|α,β)''=0，可以求出其变化率最快的点xm，如式(10):

(10)

在区间[x0,xm+]内，既能够保证Gamma分布函数值较大，同时也能够保证距离衰减速率较快，从而让距离衰减权重真正发挥作用。

综上，距离感知权重wd的计算公式如式(11):

(11)

其中，dist≥0。

2.2 类别负载权重wf

记数据集一共有N个样本，每个类别的样本数为Ci(i=1:m)。假设抽样是随机的，则用于训练的样本的分布和总体的分布是一致的，考虑不同类别数量的差异性，假设不同类别的数据之间相对独立，其出现的概率分布P={p1,p2,…,pn}。其中pi的计算方式如式(12)所示:

(12)

则类别的自信息Ie=-log(pi)，即类别被选中的概率越小，其在实际决策的时候，所蕴含的自信息越大，即事件发生时，其能够减少不确定性的程度越大。在考虑类别负载权重时，对于自信息越大的类别应该更加重视，其权值也更大。

令wfi=Ie，得式(13)：

(13)

对于这样一个决策系统，系统自信息的期望值H如式(14)所示：

(14)

实际上，H是这个系统的熵值，熵值越大，其在决策前，不确定性越大。容易证明，当pi=1/m时，即每种类别出现的概率一致时，H有最大值H0=log(m)。此时外部数据的噪声对系统影响最小。即，在实际决策时，熵的减少最大限度依赖于KNN模型的有效计算，而不是初始的系统分布。特别地，如果数据集分布不均，类别预测时，会较大程度受到系统初始分布的影响，KNN决策时对熵减小的贡献度有损失。

一般KNN的K的取值范围为3～15，不会过大，过大容易倾向于分类为数量较多的类别；也不宜过小，否则容易受到噪声数据干扰。

函数在前期变化剧烈，当类别比例差距足够大时，变化相对缓和。例如，两个类别的数据量差距在100倍左右时，权值差距在4.5倍左右；而类别数据量差距在1 000倍左右时，权值差距在7倍左右。权值差距倍数与超参数K的取值相当，能够较好权衡类别数量差距带来的影响，从而实现根据数据集的差异进行动态加权。

2.3 G-WKNN算法流程

记有n个训练样本，样本的维度数为m，一共有M个类别C1～CM，算法输入包括了训练数据Xn,m，测试样本P1,m。算法实现过程如算法1所示。

算法1：G-WKNN算法实现

输入:训练样本数据X，标签Y，以及待测样本P

输出:待测样本的分类结果Ci

1. 初始化K、α和β

2. FORitondo

3. disti←0

4. FORjtomdo

5. dist←‖Xi-P‖ /*计算Xi与P之间的欧几里得距离*/

6. END FOR

7. END FOR

8. dist←Sort(dist) /*对距离向量升序排序*/

9. 选择dist的前K个元素

10. 初始化score，每个类别均为0

11. FORktoKdo

12. /*f(k)是第k个元素对应的类别映射*/

13. scoref(k)←scoref(k)+wf(k)×Gamma(distk+x0|α,β)/Gamma(α,β)*

14. END FOR

15. score←ArgSort(score) /*对score降序排序，返回下标*/

16. RETURNf(score[0])

3 实验与结果

为了验证G-WKNN模型，使用公开数据集对模型的准确率、稳定性以及参数灵敏度等指标进行了对比实验。

3.1 实验数据集

CIC-IDS2017数据集从2017年7月3日(星期一)开始搜集，于2017年7月7日(星期五)结束。主要攻击类型包括暴力破解FTP和SSH、DoS、Heartbleed、Web攻击、渗透、僵尸网络和DDoS。

数据集正常流量类数目相对较多，流量呈现高度分布不均，正常流量占到了80%，对于部分异常流量，其占比不超过1%。对数据集做了如下调整，剔除了部分数据量极少的异常流量，如Sql Injection类型的异常流量，同时对正常流量抽取一部分作为实验数据。

3.2 评价指标

实验中使用了混淆矩阵、准确率、精确度、召回率和F1值对模型进行评估。

其中准确率的定义如式(15)：

(15)

精确度表示预测为正样本中，被正确分类的比例，如式(16)所示:

(16)

召回率表示对于真实的样本，预测为正样例所占比例，如式(17)所示:

(17)

而F1分数兼顾了模型的精确率和召回率，其表达式如式(18)所示:

(18)

其中，TP、FP、TN和FN的含义如下:

在二分类的情况下，TP表示正例被预测为正例；FP表示正样例被错误识别为负样例；TN表示负样例被正确识别为负样例；而FN表示负样例错误地被预测为正样例；多分类计算方式同理。

3.3 少数类分类性能测试

从实验数据集中按类别比例抽取10 000条数据作为实验数据。其中数据集不均衡对分类准确率的影响主要体现在训练数据上，即那些被标记好用于未知样本分类的数据，实验中随机按类别比例抽取数据集的一部分作为训练数据，剩下的数据再按照分层抽样，每个类别抽取固定数量的数据用于结果测试。

使用原始的KNN，在K取值为3、5和7的情况下，测试结果的混淆矩阵如图1(a)、(b)、(c)所示。在数量较少的类别，如Bot、BruteForce和XSS三类攻击的分类效果相对较差，分别对应于混淆矩阵的第二行和最后两行。尤其是XSS攻击类别，对应的混淆矩阵的值仅有0.04左右。

在固定参数α=4、β=5的情况下，G-WKNN的表现如图2(a)、(b)、(c)所示。除了总体分类效果有提升外，对于数量较少的类别，其分类准确率有比较明显的提升。Bot、BruteForce和XSS三类攻击对应混淆矩阵的值达到了0.8、0.6和0.5左右。混淆矩阵的对角线更加突出，模型对少数类别分类的准确率有提升。

图1 原始KNN分类混淆矩阵

图2 G-WKNN分类混淆矩阵

3.4 参数α和β灵敏度分析

为了对比不同α和β参数对模型分类效果的影响，本节设计了参数α和β敏感性分析实验，以验证模型的稳定性和解释参数选择的合理性。

选择不同α和β，测试模型的分类准确率，对比不同K值情况下模型的稳定性，实验结果如图3所示。

图3 α和β参数对模型准确率影响

参数K在9至17时，参数α和β的选择对模型准确率影响不显著，模型准确率基本维持在0.89上下；但在K值较小或者较大时，α和β对模型分类准确率影响变大。

同时，无论α和β的取值如何变化，模型准确率较高的点首次出现于K=9前后，虽然一些模型随着K增大，其准确率还会略有增长，但不明显。当K值过大时，此时权值差距倍数与K值相差较大，模型的准确率会受到一定程度影响；尤其对于衰减区间长度较长的模型，其准确率下降较为显著，此时模型动态加权的能力减弱。

3.5 参数K灵敏度分析

K是KNN模型关键的超参数。为此，本节设计了不同模型对参数K灵敏度分析实验，以验证G-WKNN模型的有效性。

固定参数α和β,对比分析了几种改良KNN模型的灵敏度，测试数据如表1所示。总体而言，加权KNN的表现比原始KNN更好；而G-WKNN的表现更佳，比1/d型的KNN准确率高，并且受超参数K的影响更小，同时对于超参数α和β，模型表现不过于灵敏。

表1 实验结果

就模型分类准确率而言，对K值从3到21逐一测试，原始KNN和三种WKNN的对比结果如图4所示。

G-WKNN的准确率基本维持在0.9，对K选择敏感度低；其余两种WKNN相对稳定，但准确率在0.85和0.8左右；而原始KNN对K的选择较为敏感，模型预测准确率容易随着K的取值发生较大波动；G-WKNN具备较好的调节能力，其准确率波动更小，模型更加健壮。

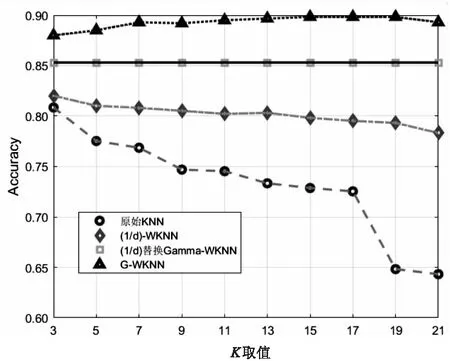
图4 K取值对预测准确率的影响

将1/d加权方式替换Gamma内核，替换后的模型，其分类准确率比原始的1/d-WKNN更好，更稳定，证明了类别负载权重调节的有效性；但准确率比G-WKNN低，说明了在合适的参数α和β下，Gamma分布函数对于样本距离加权调节更加有效。总体而言，G-WKNN分类准确率的波动更小，其准确率比另外两种WKNN也更高。

3.6 数据集均衡分布对模型的影响

为了说明不均衡数据集对模型准确率的影响，本节设计了分层抽样实验，通过分层抽样，能够将每个类别的训练数据集控制在相当的范围，测试样本不变。由于XSS类别数目最少，仅有600余条，选择75%作为训练集，各个类别采样均为450条。此时，不同KNN模型分类结果如图5所示。

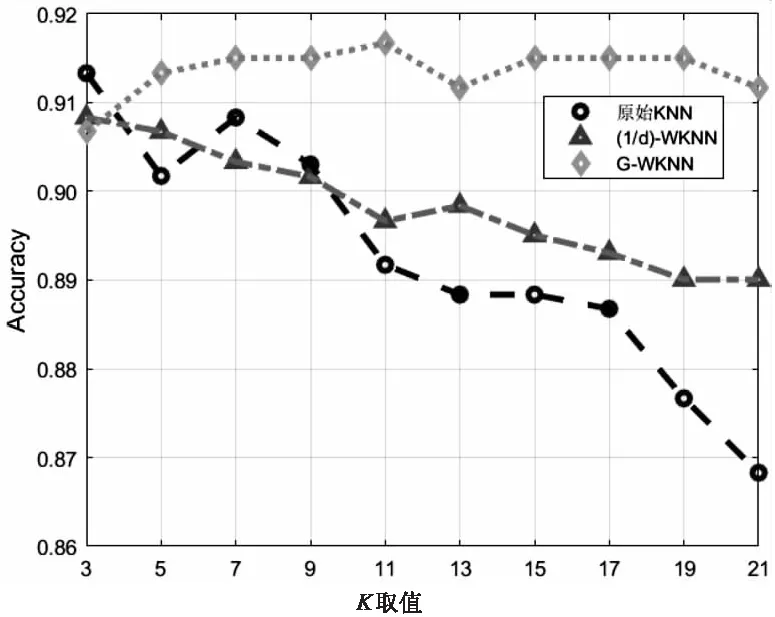
图5 数据集分布均衡下各个模型分类准确率

从图5可以看出，在数据集分布均衡的情况下，三种模型的分类准确率均有不少提升，但从稳定性和分类结果看，原始KNN和1/d-WKNN对于超参数K较为敏感，模型分类准确率不稳定，而G-WKNN分类准确率基本维持在0.91以上。

在类别均衡的情况下，类别负载权重wf作用被削减；特别地，若类别绝对均衡，则类别负载权重退化为1，此时距离感知权重发挥调节作用，从实验结果可以看到，Gamma内核对分类器的调节是有效的，G-WKNN分类准确率始终高于其他两个模型。

3.7 模型运行时间性能分析

为了说明模型运行时间性能，本节设计了对比实验。实验数据集数量为10 000条，在测试数据集为每个类别50例的情况下，对比了原始KNN和G-WKNN的运行时间，如表2所示。

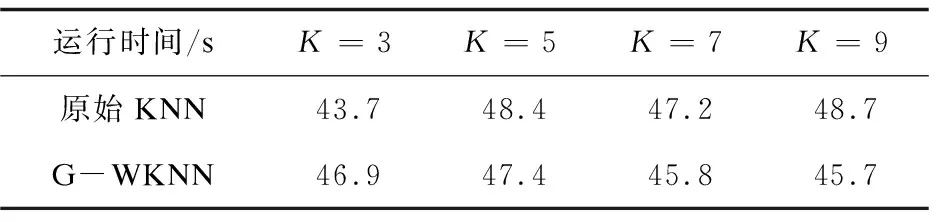
表2 模型运行时间实验结果

由表2可知，G-WKNN在运行时间上尽管优势不显著，与原始KNN运行时间相当，但模型在准确率上的提升较为突出。

3.8 数据集数量对模型的影响

为了说明数据量大小对模型的影响，本节设计了对比实验，通过调节参与分类的数据集的数量，对比不同模型的分类准确率。

实验结果表明，通过增加训练数据集，一定程度上缓解了数据集不均带来的问题，如图6(a)、(b)和(c)所示。增加训练数据集后，三种模型分类准确率有一定的提升，原始的KNN通过增加数据集准确率最高达到了0.85；而1/d-WKNN随训练样本数量的增加，分类效果也有一定的提升；G-WKNN模型的准确率基本维持在0.88至0.90。这说明，通过增加数据集数量的方式，一定程度能够缓解数据集不均带来的分类准确率下降的问题。

但在实际情况中，数据集往往分布不理想，同时数据集数量可能有限，G-WKNN算法能够在数据集较少，并且分布不平衡的情况下，达到比较高的分类准确率。数据集数量对模型准确率影响较小，模型较为稳定。

图6 三种模型在不同数据量下的分类准确率对比

4 结束语

G-WKNN算法缓解了数据集分布不均带来的类别倾向问题。通过设计距离感知权重和类别负载权重，分别调节类别间的差异和样本间的差异。对于类别分布不均的数据集能够自动适应数据集的倾斜程度，其表现优于传统KNN和简单的1/d-WKNN，并且结果更加稳定；在分类结果中，针对数目较少的类别，其预测的准确率有比较明显的提升。这对于倾斜分布的数据集以及数据集较少的情况，分类效果有较为明显的改善。同时，分类效果也不能仅仅依赖于权重函数的设计，实验结果也表明，在相同的情况下，分布均匀的数据集，分类器的表现会更加突出和稳定。