基于同步性脑网络的注意力识别研究

王励烨，丁威威

(南京邮电大学 电子与光学工程学院 微电子学院，江苏 南京 210023)

0 引 言

一直以来，人的注意力状态的实时监测在教育领域以及交通安全领域都有广泛的需求，早期的注意力检测多采用面部识别等基于视频图像信息的方式，而随着脑机接口技术的发展，基于脑电信号(Electroencephalogram，EEG)的注意力检测方式已经成为了研究的热点。脑电信号是一种典型的生物电信号，是大脑神经细胞生理活动在大脑皮层及头皮的总体反映，与人的各种生理、心理活动相关。相比于表情等信息，脑电信号能更真实地反映人的大脑状态。

传统的基于脑电信号的注意力研究主要提取信号的时域和频域信息进行分析。例如，陆荣等[1]利用小波包分解的方法，提取各个频段的脑电信号，并计算这些频段的近似熵作为特征输入支持向量机(Support Vector Machine，SVM)分类器内进行分类，其准确率达到了72.5%。孔亮等[2]采用谱分析的方法，提取各节律能量的比值作为特征，同时结合特征的特点，设计多层误差反向传播(Error Back Propagation Training，BP)神经网络作为分类器，注意力分类准确率在77%左右。然而越来越多的研究表明，大脑是一个复杂的网络，随着大脑状态的改变，脑网络的拓扑结构也随之发生变化[3]，大脑的各种状态是网络各个区域共同作用的结果，单纯从时频域提取特征会忽略大脑状态改变所产生的结构性信息。随着复杂网络理论的发展，基于EEG信号的脑网络研究成为新的研究方向。

目前已有将EEG脑网络应用于注意力相关的研究，如Chabot等[4]对130名儿童的脑电信号进行了相关性分析，发现相较于正常儿童，患有注意缺陷多动障碍综合征(Attention Deficit Hyperactivity Disorder Syndrome，ADHD)的儿童在θ和α频段其前额叶两半球间，以及前额叶-颞叶两侧区域的半球间的相干性更高。可见人的注意力状态可以从相干性脑网络中得到反映，但需要在实验中进一步进行验证。 吴正平等[5]通过相空间重构将单通道脑电信号转换成复杂网络结构，进而提取专注和放松状态下的网络特征度量，实现对注意力水平的检测，并设计了一种优化的复杂网络算法(OCNM)对其进行分类，注意力二分类准确率达到80.67%。该算法考虑到了导联信号之间的关联性，并使用网络分析的方法提取特征，分类准确率得到了显著提升，但网络分析的特征提取办法较为复杂，算法无法实现实时性的注意力检测。

针对以上研究现状，该文设计了注意力状态和非注意(注意力分散)状态的实验范式，并采集脑电信号，提出了一种基于同步性脑网络和信息增益的注意力分类算法(Algorithm of Synchronous Brain Network and Information Gain for Attention Classification，SBN-IG)。该算法使用脑电信号计算PLV值并构建同步性脑网络作为分类器的输入特征，PLV由Lachaux等人在1999年提出，通过计算脑电信号的各个导联之间的锁相值，能很好地反映相应脑区之间在任务期间的同步性[6-7]。考虑到SVM使用向量的输入形式，忽略了脑网络结构信息，采用卷积神经网络(Convolutional Neural Network，CNN)[8]作为分类器对网络结构特征进行提取与分类。而为了上述算法能应用于实际，在将特征矩阵输入分类器之前对其进行特征稀疏化，减少实际需要的导联数，降低算法运行时间，满足注意力实时监测的应用需求。

1 SBN-IG注意力分类算法

提出的SBN-IG算法架构如图1所示。第一步：数据采集。根据需求设计实验范式，并招募被试进行相关状态的脑电信号采集。第二步：预处理。对采集的数据进行预处理，降低噪声，提高信噪比。第三步：生成同步性脑网络，经过预处理的脑电信号计算导联之间的PLV，构建同步性脑网络，PLV矩阵作为分类的特征，输入卷积神经网络进行分类(SBN)。第四步：特征稀疏化，虽然直接对脑网络特征进行分类已经可以得到很好的结果，但仍存在算法效率较低的问题，因此引入特征稀疏化算法剔除冗余特征，再将稀疏化后的特征矩阵输入分类器(SBN-IG)。

图1 算法结构

2 数据采集

为了获得稳定的注意力集中与分散状态的脑电信号样本，分别设计了对应的实验范式，实验流程如图2所示。注意力状态实验：使用Aim Trainer测试范式[9]作为注意力集中的诱发范式。在范式中，被试需要完成一个点击小游戏。系统会在1 920×1 080像素的显示屏上随机产生一个直径为2.5 cm的目标圆点，被试需要在尽可能短的时间内移动鼠标点击圆点，准确点击后该点消失，并重复之前的过程。在被试完成10分钟的点击任务之后，游戏结束。非注意状态实验：屏幕将会播放当前被试在注意力状态实验中的屏幕录像，被试需要一直注视屏幕同时尽量保持放松状态，无需进行任何操作，实验同样持续10分钟，在实验开始后10 s左右开始采集脑电信号。实验设计采用10分钟这一较长的实验时间主要是有以下两个考虑，首先是经验表明游戏因其特殊性更能激发并保持人的注意力集中状态，在此期间被试不会产生疲惫等负面状态，其次被试在较长时间的注意力高度集中状态后更易进入注意力分散状态，因此选择让被试在完成第一个诱发实验后一段时间进行第二个诱发实验。在对实验器材的预测试中，较长的实验时间不会对数据的采集造成影响，也并未产生导电胶固化等问题。

图2 实验流程

以上所有实验均在被试同意且签写知情同意书的前提下完成，共招募被试32人，身体健康无精神病史及其他心理疾病(50%男性,50%女性)，年龄范围为19～24岁(平均值=20.95,标准差=4.23)，每次实验前会将被试平静状态的脑电信号作为参考，两次实验之间间隔十分钟，每名被试分别完成两种状态下的实验，共获得两种状态标签数据各32段，共64段标签数据。

实验使用NeuroScan公司的64导联电极帽进行数据采集，电极分布如图1(a)所示，符合国际10～20标准的导联系统，采样频率为500 Hz，采样阻抗低于5 kΩ，使用Curry7软件进行参数设置并导出采集到的脑电信号。

3 数据预处理

为了降低信号的冗余度，提高后续分类的准确率，使用EEGLAB软件对原始脑电数据进行预处理。依次进行带通滤波、信号重参考[10-11]、独立成分分析(Independent Component Analysis，ICA)[12-14]、时频域截取的处理，下面分别进行介绍。

带通滤波：由于清醒状态下人的大脑活动产生的相关信号频率可以分为θ波(4～8 Hz)、α波(8～12 Hz)、β波(12～30 Hz)和γ波(30～80 Hz)[15]，大脑注意力信息集中在θ、α、β频段，且在脑电采集过程中由于人体生物电或者环境因素的影响，会产生较大的工频干扰信号，主要集中于50 Hz左右[16]。因此，为了保留有效脑电信号，去除工频干扰信号的影响，该文采用带通滤波(1～40 Hz)方法对原始信号进行第一步处理。

信号重参考：参考电极的信号被认为是其他所有信号的基线信号，信号的重参考就是从其他信号中剔除参考电极的信号成分从而消除来自接地电极的噪声。该文采用的参考电极位置为10～20电极标准中左右耳后乳突的位置，对应电极为M1与M2(如图1(a))。因此第二步将M1与M2设定为参考电极进行信号的重参考。

独立成分分析：ICA是盲源分离(Blind Signal Separation，BSS)的一种方法，将混合的信号分离成潜在的信息成分。脑电信号是一种大量噪声和有效信号相混合的混合信号，针对这种信号，使用ICA可以很好地检测、分离和消除EEG记录中的各种伪迹。第三步对信号进行ICA，该文使用MATLAB的EEGLAB插件提取信号中的独立成分，ICA算法种类选择默认的runica算法。在提取出脑电信号中的各个独立成分后，可以在EEGLAB上对所有成分的头皮地形图进行显示(如图1(b))，并对照眼电、心电等成分的地形图特征对这些噪波进行手动经验剔除，能极大地提高信号的信噪比。

4 生成同步性脑网络

预处理去除了信号中的噪声部分，为了针对性分析特定时段与频段的信号，需要对信号进行时频域截取。选择进入注意力状态后的3 s作为时间窗口进行截取，由于采样频率为500 Hz，因此每段样本长度为1 500个点。32位被试分别完成两种注意力状态实验。获得数据样本共64段。同时，该文分别对每个样本段提取θ波、α波、β波三个频段的信号，共有64×3=192个频段样本。

通过小波变换提取出信号的瞬时振幅和相位。某导联在时频坐标下的瞬时相位值记为Φ(t,f)，则一对导联之间的PLV的计算如公式(1)：

(1)

其中，N为总采样点数，文中每个样本采样点数为1 500；t为当前时间，f为频率，x、y为一个导联对，ΔΦn(t,f)为第n个采样点当前导联对的瞬时相位差：

ΔΦn(t,f)=Φx(t,f)-Φy(t,f)

(2)

另记时频映射中频率点数目为L，可以通过计算频域映射的分辨率与当前频段的频带宽度的乘积得到，对公式(1)针对频域取平均得到该导联对的平均PLV值为：

(3)

PLV取值在0到1之间，两个导联间PLV值越接近1则代表两者的同步性越强， 越接近0则同步性越弱。将预处理后的信号按照公式(3)进行PLV值计算，每个样本可以得到一个64×64的PLV矩阵，如图3所示。从图中可以看出，由于脑电信号信噪比较低的特点，无法直观地从图中发现两者的区别，但可以使用卷积神经网络提取其中的细节特征，获得了SBN算法，该算法通过后续的仿真验证，获得了较高的准确率。但考虑到算法的实际运用需要更少的导联以及更短的运算时间，又引入了算法实现对PLV矩阵的稀疏化，提取最重要的导联连接作为分类器输入特征。

图3 平均PLV矩阵示意图

5 特征稀疏

特征稀疏化算法的流程如图4所示。输入特征为PLV矩阵，先后经过二值化、信息增益计算、特征保留的步骤得到稀疏化的矩阵输出并作为新的特征输入分类器分类。与原始PLV矩阵相比，稀疏化后的矩阵因为只保留了重要特征，剔除了冗余特征，有利于提高特征提取效率与算法训练的拟合效率。

图4 特征稀疏算法流程

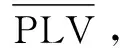
(4)

对于每个PLV特征，若其大于阈值则置1，小于则置0。

该文采用了一种基于信息增益的阈值确定方法，该方法会遍历当前特征在所有样本中的值，依次将其设为阈值并计算当前阈值下特征的信息增益，最终选择其中产生最大信息增益的阈值为该特征的PLVT。

从信息论的角度，特征的稀疏化过程就是去冗余过程。目前常用的特征冗余度评价方法主要有信息增益[17-18]和卡方检验[19]。这两种方法已经在文本识别领域得到了广泛使用。考虑到本算法的特征数量多、分类类别少，且脑电信号信噪比低的特点，该文采用信息增益判断PLV矩阵的冗余度。用公式(5)来衡量特征对系统的信息贡献度：

IG(t)=∑P(Ci)logP(Ci)+

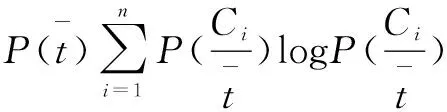
(5)

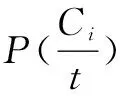
综上，该文实现了一种基于信息增益的特征稀疏化算法，特征矩阵在输入后首先进行二值化得到离散特征矩阵，然后计算矩阵每个特征元素的信息增益并以此对特征进行排序，最终保留信息增益最大的k个特征组成特征矩阵输出。

6 注意力分类

使用稀疏化矩阵输入卷积神经网络进行分类，将数据样本按照3∶2的比例随机分配为训练样本和测试样本进行交叉验证。为保证准确性，将此过程重复多次，保证每次对样本的分配都是随机且不同的。

参考经典的LeNet-5[20]结构构建卷积神经网络，构建了基于PLV脑网络的卷积神经网络，结构如图5所示。

图5 卷积神经网络模型

神经网络的前6层由卷积层和池化层间隔组成，卷积层可以提取输入的不同特征，多个卷积层组成的网络能提取较为复杂的特征，每个卷积层的输出都经过线性整流(Rectified Linear Units，ReLU)函数的处理，用来增强网络的非线性特性，在池化层输入特征按照池化函数进行了一次降采样，池化层可以降低数据的空间大小，从而降低参数的数量与计算量。模型的最后两层分别为全连接层与高斯连接层，前者将输入的矩阵展开为向量，后者为一个简单的两层BP神经网络结构，通过对输入特征向量的学习最终输出为两个结果，对应判断结果为注意力集中或者注意力分散。

7 结果与讨论

在未加入特征稀疏步骤前，对SBN算法的准确率进行了一个测试，提取θ、α、β频段的PLV特征矩阵，每个频段均进行了60次同条件分类准确率测试并绘制相应的统计图，不同频段数据的分类准确率盒须图如图6所示。由图6可以看出，θ波频段的特征分类准确率分布最为集中，且从平均分类准确率(θ频段：90.90%，α频段：85.71%，β频段：87.76%)上，θ波频段的特征亦得到了最高的平均分类准确率，因此，选择该频段作为算法的信息采集频段。

图6 分类准确率盒须图

至此，利用θ频段的同步性脑网络特征实现了注意力的状态分类，准确率高达90.9%。但这种方法在计算中的耗时仍是较大的，这主要是因为特征矩阵的维度较高，特征数量较多，如果将它们全部计算会极大降低计算的效率。为了解决这一问题，在算法中加入了特征稀疏化步骤，构建了SBN-IG算法。

为了验证SBN-IG算法的效果，分别对θ频段不同稀疏化强度的分类效果进行了测试，在进行多次预测试后，该文选择从保留前10个特征开始，依次降低特征数量直至1个特征，每个特征数量情况进行60次同条件的准确率测试。θ频段十种稀疏化强度的分类准确率的盒须图如图7所示。

图7 特征数量与分类准确率盒须图

可以看出在特征数从8个(平均分类准确率：86.88%)转变为7个(平均分类准确率：81.16%)后，平均分类准确率明显下降，分类准确率分布明显分散，因此选择保留8个特征作为特征选择的结果，此时平均分类准确率为86.88%，在此稀疏化强度时，将需要的特征数量从4 096个(64×64)降低到8个，这大大提高了计算PLV矩阵的效率，为实现实时注意力检测的目标提供了可能。

对SBN-IG算法保留的8个特征进行了统计，如表1所示。

表1 保留特征的统计结果

从表1可以看出，筛选出的特征在注意力集中状态的平均值要低于注意力分散状态，且从这8个特征对应的13个电极可以看出，电极多位于大脑顶叶与枕叶位置，这也与文献[4]中得出的在θ频段患有ADHD儿童两半球间相干性更高的结论相吻合，进一步验证了算法的有效性。

为了更直观地展现算法的性能，选择了文献[1-2,5]中分类的算法进行比较，所有算法均使用文中设计实验所采集的脑电信号，且均根据文献描述完成了相应算法的构建与特征的提取，最终分类结果如表2所示。

比较所有算法的结果看出，在使用相同数据集的情况下，采用脑网络特征的算法得到了较高的分类准确率，说明脑网络特征能较好地反映大脑的注意力状态。在所有算法中，SBN算法得到了最高的分类准确率，算法的可行性得到了验证，同时，从算法效率上考虑，实际测试中在相同环境下分别对SBN与SBN-IG算法的分类平均用时进行了测算，测算方法为调用Python的time库对算法运行的各个阶段进行计时。结果表明，在扣除了算法训练用时后，对一段3 s的脑电数据完成分类，SBN算法用时20.635 1 s，其中18.374 4 s用于数据预处理，SBN-IG算法用时1.730 5 s，其中0.264 9 s用于数据预处理。可以看出，相比于SBN算法，SBN-IG算法的效率得到了较大提升，具有更高的应用价值。

表2 各分类算法比较

8 结束语

该文提出了一种新的基于同步性脑网络的注意力分类算法SBN。实验结果表明，该算法针对注意力集中与分散两种状态有很好的分类效果。同时，为了解决该算法计算效率较低，无法实现实时注意力检测的问题，设计并构建了一种新的基于同步性脑网络和信息增益的注意力分类算法SBN-IG。该算法在SBN算法的基础上加入了特征稀疏化步骤，在保证一定分类准确率的前提下，降低了算法需要计算的特征数目，从而提高了算法的运算效率。因此具有很高的应用价值。

在未来的工作中，会对两个算法做进一步的优化，另外，考虑到同步性脑网络特征重视结构性信息却忽略了时域信息，可以引入一些能够提取信号时域信息的算法如循环神经网络等来扩展算法的结构，以进一步提高算法的分类效果。