基于分段交错不等磁极的表贴式永磁电机极频振动的削弱

李泽星 夏加宽 刘铁法 郭志研 朱启升

（1.沈阳工业大学电气工程学院 沈阳 110870 2.中国科学院沈阳自动化研究所 沈阳 110169）

0 引言

永磁电机具有结构简单、功率密度高、效率高等优点，被广泛用于水下航行器推进系统[1-2]。然而，隐蔽性作为水下航行器的重要指标，容易受到永磁电机低频振动噪声的影响[3]。

极频振动又被称为2 倍频振动，主要由2 倍频电磁力谐波引起，在低频段十分显著[4-9]。文献[4]对一台8 极48 槽整数槽永磁同步电机进行了电磁振动噪声研究，结果表明，2 倍频振动噪声是最主要的峰值点。文献[5]对一台10 极45 槽分数槽永磁电机进行电磁振动特性分析，结果表明，2 倍频处的电磁力峰值与振动加速度均远大于其他频率分量。文献[6]采用模态叠加法，分析了一台外转子永磁电机在不同槽口宽度时的振动噪声特性，结果表明，2倍频振动均为主要的峰值点。2 倍频电磁力谐波主要由基波磁场作用而成，是低频段幅值最大的电磁力谐波，这导致极频振动普遍且显著存在于各类永磁电机中[7-9]。因此，针对极频电磁力的分析和削弱是十分必要的。

目前，国内外已有许多学者对电机振动噪声的削弱方法进行了研究[10-15]。文献[10]以一台2 极24槽永磁电机为例，提出了一种转子表面插入铜环的方法来削弱振动，实验结果表明，该方法主要用于高频振动分量的削弱，对低频振动的削弱效果并不显著。文献[11]以一台4 极24 槽外转子永磁电机为例，对比了之字形磁极结构与斜槽两种方法的振动削弱效果，结果表明，之字形磁极结构优化效果更加显著，该方法主要用于槽频振动的削弱。文献[12]以一台8 极48 槽永磁电机为例，基于麦克斯韦张量法，分析了转子分段斜极对电机径向力波谐波的影响，结果表明，通过选择合适的分段数与倾斜角度，理论上可有效削弱相应的电磁力谐波，但该方法用于2 倍频电磁力的削弱时，平均转矩将会显著降低。文献[4]提出一种优化的隔磁桥结构，2 倍频电磁力谐波幅值显著降低，但是平均转矩也明显下降。此外，还有齿顶偏移[13]、定子齿削角[14]、斜槽[15]以及不同心永磁体[16]等优化方法，但是这些方法在用于极频振动的削弱时，都有一个共性问题，即影响基波磁场，导致平均转矩严重下降。2 倍频电磁力主要由基波磁场引起，基波磁场是电机能量转换的主要媒介，基波磁场的减小往往导致电机转矩密度的降低。因此，如何在保证平均转矩基本不变的情况下，提出一种可靠的方法，有效削弱极频振动是一个亟待解决的问题。

本文提出了一种分段交错不等磁极的优化方法，该方法可通过调节磁极过零点轴向位置来削弱极频振动，且基本不影响转矩密度。首先，基于麦克斯韦张量法，推导了作用于齿部的集中电磁力，分析了集中电磁力曲线与磁场过零区域的关系，得到了极频振动的产生原因。其次，提出分段交错不等磁极结构，分析了该结构削弱极频振动的机理。然后，基于有限元模型，对比了优化前后电机的电磁性能及振动频谱。最后，搭建了优化前后样机的振动实验平台，验证了优化结构的有效性。考虑到空载状态的噪声响应即可反映该电机的噪声趋势与特征[17]，因此，为方便起见，本文主要对样机空载下的极频电磁力谐波进行分析，通过实验来验证分段交错不等磁极结构在负载工况的有效性，所得结论可以为表贴式永磁电机极频振动噪声的削弱提供有价值的参考。

1 电机模型

本文以一台10 极12 槽表贴式永磁电机为例进行分析，其横截面示意图如图1 所示。图1 中，定子齿进行了编号，转子逆时针旋转。表1 列出了电机的基本参数，磁极极弧系数为0.86。

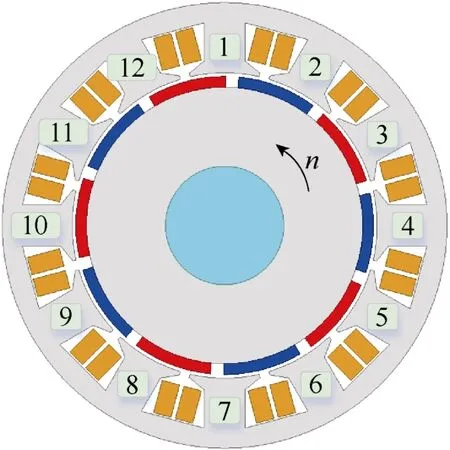
图1 10 极12 槽表贴式永磁同步电机横截面示意图Fig.1 Cross section of 10-poles 12-slots surface-mounted permanent-magnet machine

表1 样机基本参数Tab.1 The basic parameters of prototype

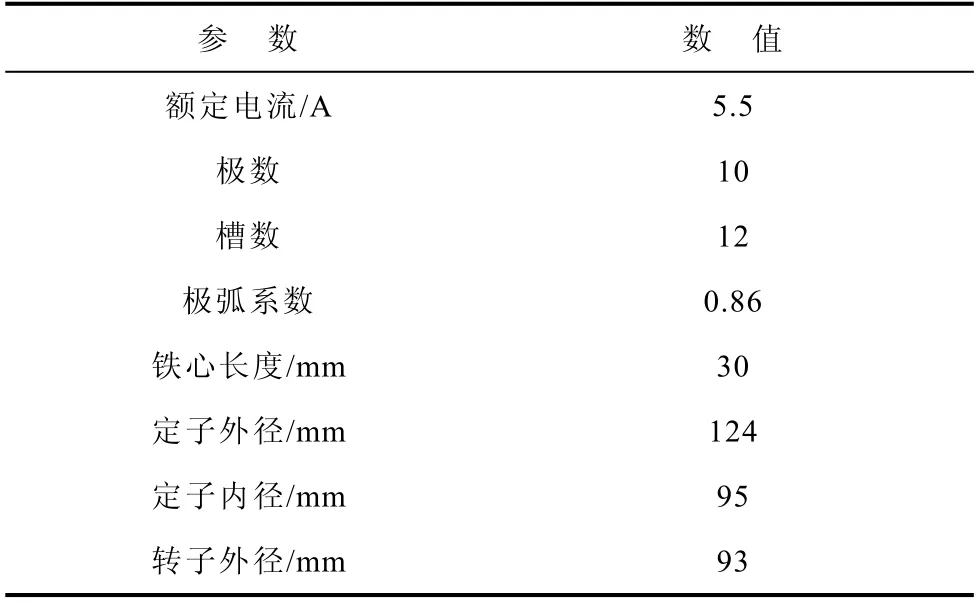
（续）

2 极频振动产生机理

2.1 气隙磁场解析模型

在永磁磁场作用下，气隙处的等效磁动势[18-19]为

式中，θ为转子位置角；p为转子极对数；ω为定子基波电流角频率；t为时间；为vR次磁场谐波的幅值，vR=2kR-1（kR=1,2,3,…），vR=1,3,5,…。

考虑定子开槽效应，等效气隙磁导可表示为

式中，λ0为气隙平均磁导；为kZ次谐波磁导的幅值；Z为定子槽数。

将式（1）永磁磁动势作用于式（2）气隙磁导，产生的气隙磁通密度[20]为

2.2 集中电磁力解析模型

根据麦克斯韦应力方程，定子齿表面单位面积受到的径向电磁力[21-23]为

由式（5）～式（7）可以得到电磁力的时空特性，见表2。可以发现，电磁力的时间谐波主要与气隙磁场谐波次数相关，对于特定的电磁力谐波，其由多个力波分量组成，这些力波分量之间磁场谐波含量不同。为方便起见，定义F(vR1,vR2)为由vR1和vR2次磁场谐波组成的力波分量。

表2 径向电磁力时空特性Tab.2 The spatial-temporal characteristics of radial electromagnetic force

当vR1+vR2=2,4,6 时，可得到一阶、二阶、三阶极频电磁力谐波，以一阶极频电磁力为例，应用磁场调制原理[24]分析极频电磁力谐波的产生原因。组成一阶极频电磁力谐波的力波分量需要满足

忽略幅值较小的磁通密度高次谐波，主要考虑1、3、5 等幅值较大的磁场谐波之间的相互作用，则一阶极频电磁力主要由F(1,1)、F(1,3)以及F(3,5)组成。也就是说，一阶极频电磁力谐波主要由基波单独作用，基波与3 次谐波相互作用，3 次谐波与5次谐波相互作用而成。由于这些磁场谐波占比较大，且基波磁场是电机能量转换的媒介，因此，极频振动在不同极槽电机中普遍且显著存在，极频电磁力谐波的削弱容易导致转矩密度的降低。

单个齿的积分区域如图2 所示，作用于第i个齿的集中电磁力为其表面电磁力密度的周向积分[25]，有

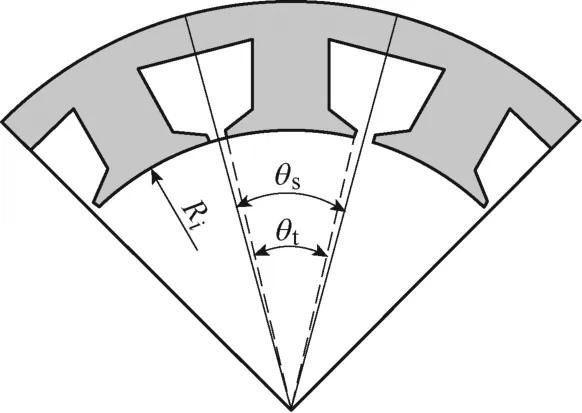
图2 单个齿的积分区域Fig.2 The integral area of one tooth

式中，θt为定子齿宽；Ri为定子内径；Lef为铁心轴向长度。

2.3 集中电磁力与磁极位置的关系

图3 为电机在空载时一对极下气隙磁通密度分布，可以看出，磁通密度幅值正负交替，其过零区域位于磁极之间，该区域磁通密度幅值在0 与曲线平顶位置（0.73 T）之间波动，波动范围较大；A、B 两个位置磁通密度也存在一定的波动，该波动由定子开槽效应引起，波动范围为0.51～0.84 T，与极间磁场过零区域相比，波动范围较小。

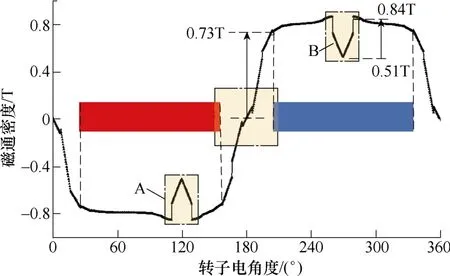
图3 气隙磁通密度曲线Fig.3 The curve of air-gap flux density

图4 为电机在空载时一对极下电磁力密度分布，可以看出，电磁力密度在0 与最大值之间波动，波动幅度最大区域在磁极之间，即磁通密度过零区域。

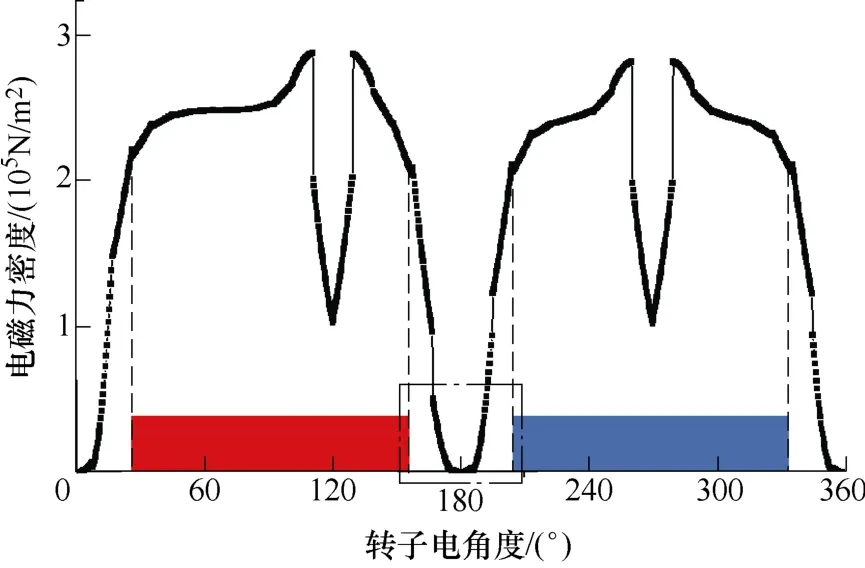
图4 电磁力密度曲线Fig.4 The curve of the electromagnetic force density

以图1 的1 号齿为例，计算额定转速空载下定子齿受到的集中电磁力，并分析集中电磁力变化趋势与转子位置的关系。图5 为1 号齿受到的集中电磁力曲线及其FFT 结果，可以看出，主要包含2f，4f，6f等电磁力谐波，其中2 倍频电磁力谐波幅值最大。集中力与转子位置关系如图6 所示。

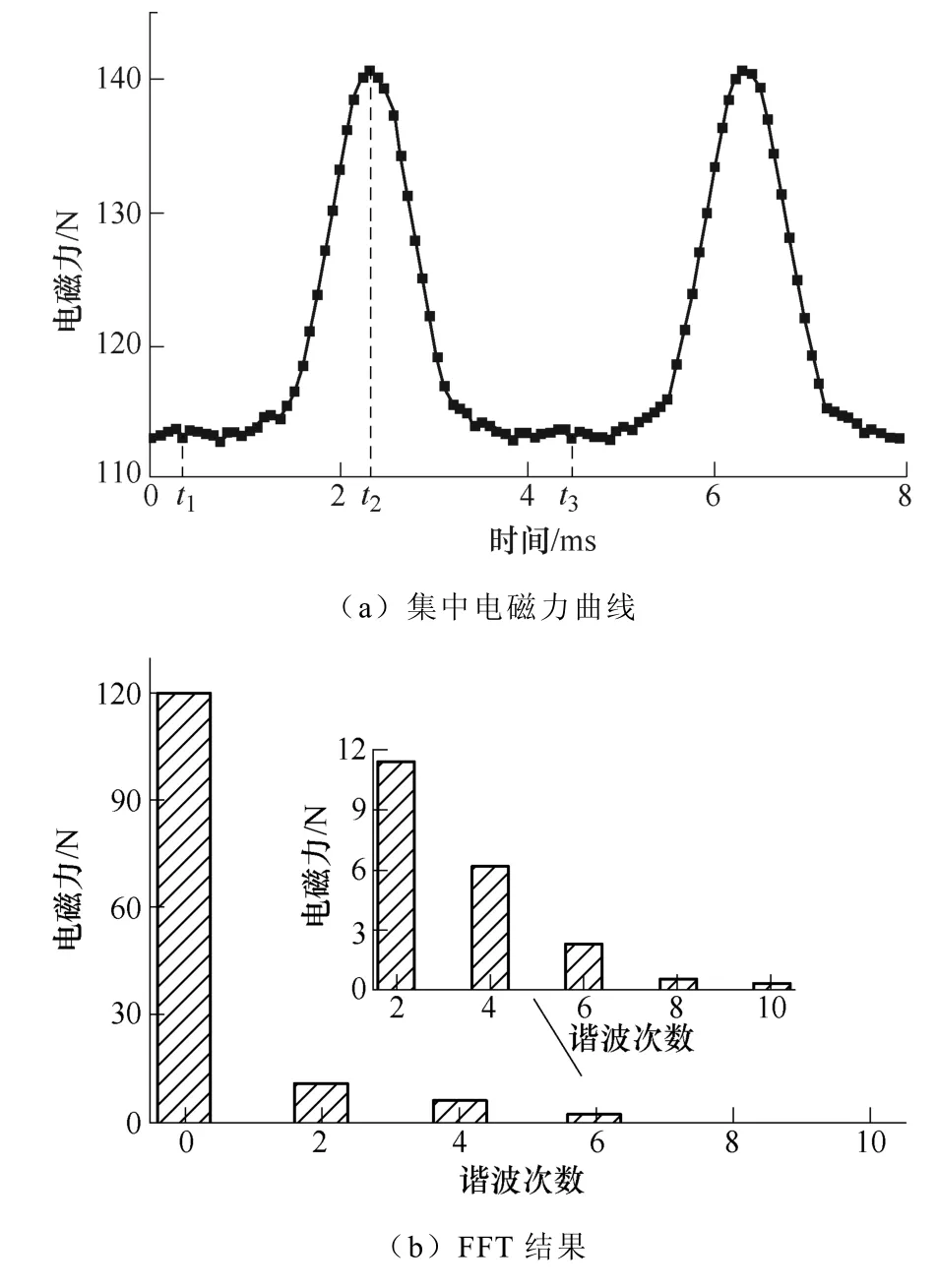
图5 集中电磁力曲线及其FFT 结果Fig.5 The concentrated force curve and its FFT result

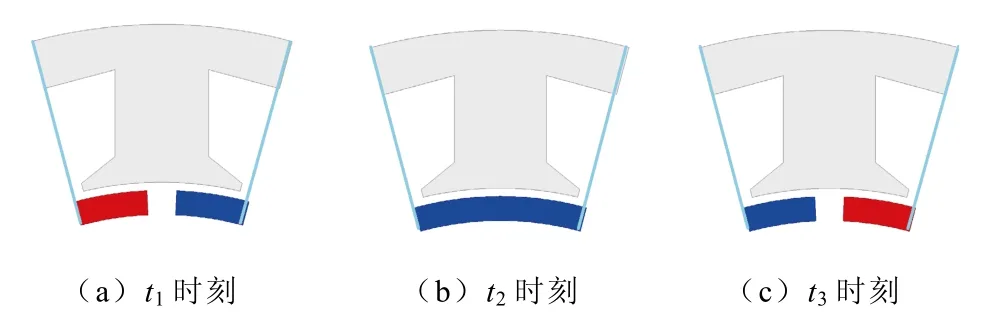
图6 t1、t2、t3 三个时刻转子位置Fig.6 The rotor position at three moments of t1,t2 and t3

（1）t1时刻，1 号齿中心线与磁场过零区域中心线重合，定子所受集中力恰好处于波谷。

（2）t1～t2时刻，过零区域由齿中心线位置逆时针旋转，定子所受集中力逐渐增大。

（3）t2时刻，齿中心线与磁极中心线重合，定子所受集中力恰好为峰值。

（4）t2～t3时刻，过零区域逆时针旋转，其中心线趋向于与齿中心线重合，定子所受集中力逐渐减小。

（5）t3时刻，齿中心线与磁场过零区域中心线重合，定子所受集中力处于波谷。

定子齿部所受集中力的波动是定子振动的主要原因。磁极交替区域存在磁通密度过零点，该位置处电磁力密度大幅波动；当磁通密度过零区域经过定子齿部时，大幅度波动的电磁力密度经过积分，导致齿部集中力在峰值与波谷之间振荡，从而引起了极频电磁力谐波以及极频振动。因此，减小磁通密度过零区域引起的电磁力密度波动可有效削弱极频电磁力以及极频振动。

3 分段交错不等磁极对极频电磁力谐波的削弱原理

3.1 分段交错不等磁极结构

图7 与图8 分别为分段交错不等磁极的3D 结构及简化模型。该结构特点如下：

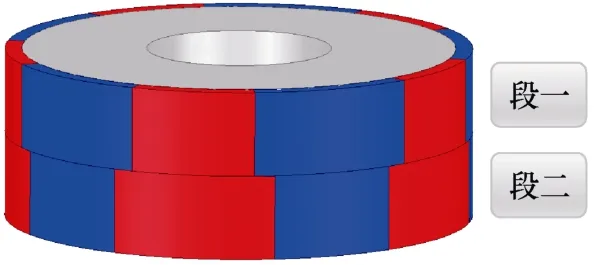
图7 分段交错不等磁极3D 结构Fig.7 The 3D model of piecewise stagger unequal poles structure

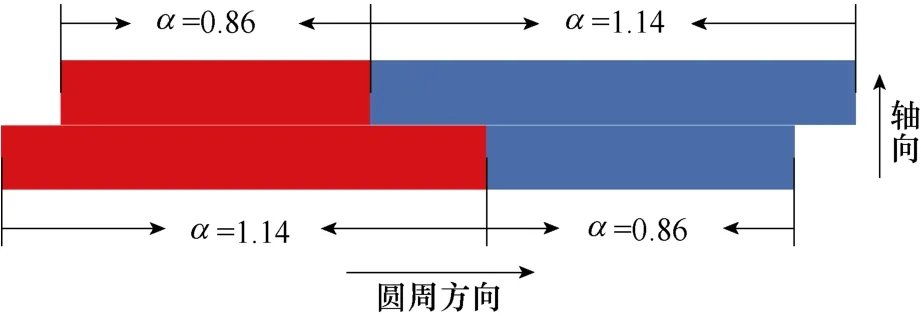
图8 分段交错不等磁极结构简化模型Fig.8 The simplified model of piecewise stagger unequal poles structure

（1）磁极在轴向方向等分为两段，两段磁极结构磁通密度过零区域在轴向偏移。

（2）在每一段转子表面，圆周方向相邻的两个磁极极性相反，极弧系数α不等，分别为 0.86 和1.14；圆周方向极性相同的磁极极弧系数相同。

（3）轴向相邻的两个磁极，极性相同，磁极中心线重合，极弧系数不同。

为方便起见，将两段磁极分别简称为段一和段二。

3.2 分段交错不等磁极结构对极频电磁力谐波的削弱

优化结构齿部集中力计算模型如图9 所示，段一和段二作用下，第i个齿所受的电磁力密度为

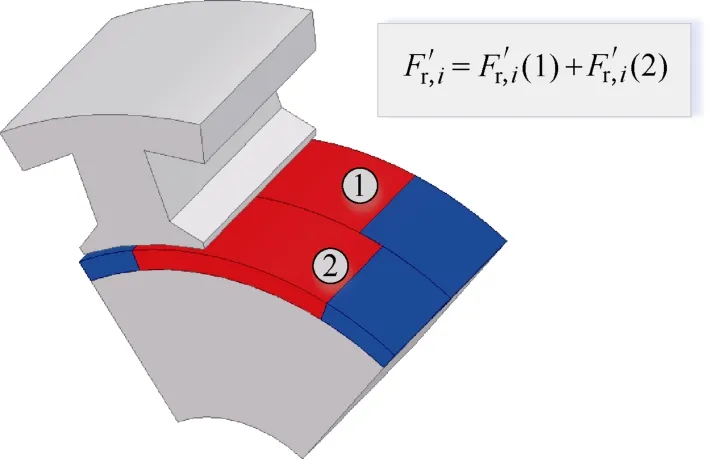
图9 优化结构齿部集中力计算模型Fig.9 The calculated model of concentrated force acting on the tooth of optimized structure

作用于第i个齿的集中电磁力为

对比图2 与图9，式（9）与式（11），可以看出：

（1）与原方案相比，优化方案不等磁极轴向交错，磁场过零区域轴向偏移。

（2）优化方案定子齿部受到的集中力为段一与段二共同作用下的合力，而原方案齿部受到的集中力在轴向一致。

（3）由于磁场过零区域偏移，采用优化方案后，段一与段二分别作用得到的集中力的波谷位置不同，在叠加后，总集中力的波谷会被填充，从而起到减小齿部所受集中力波动幅度的作用。

图10 为空载时优化电机段一与段二分别作用下的气隙磁通密度分布，可以发现，在两段磁极分别作用下，磁通密度曲线的过零区域存在明显的偏移。

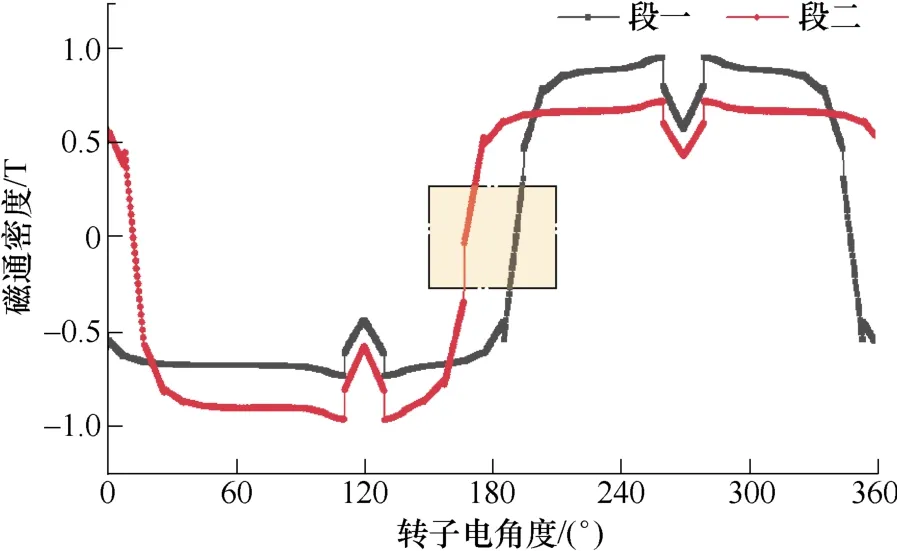
图10 段一与段二分别作用下的气隙磁通密度曲线Fig.10 The air-gap flux density curves under the separate action of section 1 and section 2

结合式（10），计算得到空载工况段一与段二共同作用时一对极下电磁力密度曲线，如图11 所示。与原方案相比，在磁通密度过零区域，电磁力密度最小值明显增大，在一个电周期内，电磁力密度曲线波动幅度减小。由图11b 可以看出，电磁力密度的二倍频、四倍频、六倍频以及六倍频谐波幅值明显降低。

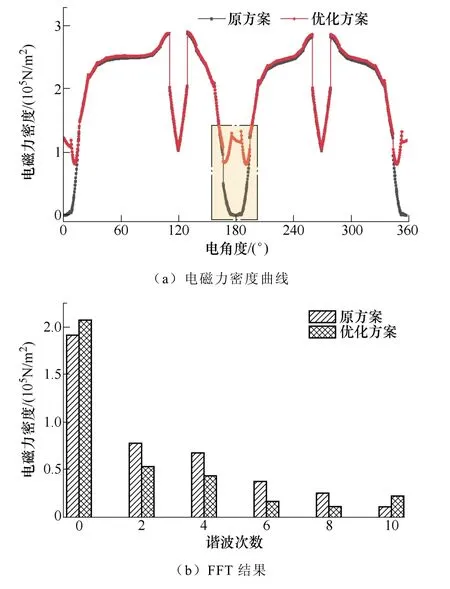
图11 段一与段二共同作用下电磁力密度曲线及其FFT 结果Fig.11 The electromagnetic force curve and its FFT result under the combined action of section 1 and section 2

结合式（11），计算得到空载下优化方案一号齿受到的集中电磁力，如图12 所示。与原方案相比，电磁力曲线波动幅度明显减小。由图12b 可以发现，优化方案二倍频电磁力降低52 %，四倍频、六倍频以及八倍频也有明显的降低。因此，分段交错不等磁极结构可有效削弱极频电磁力谐波。

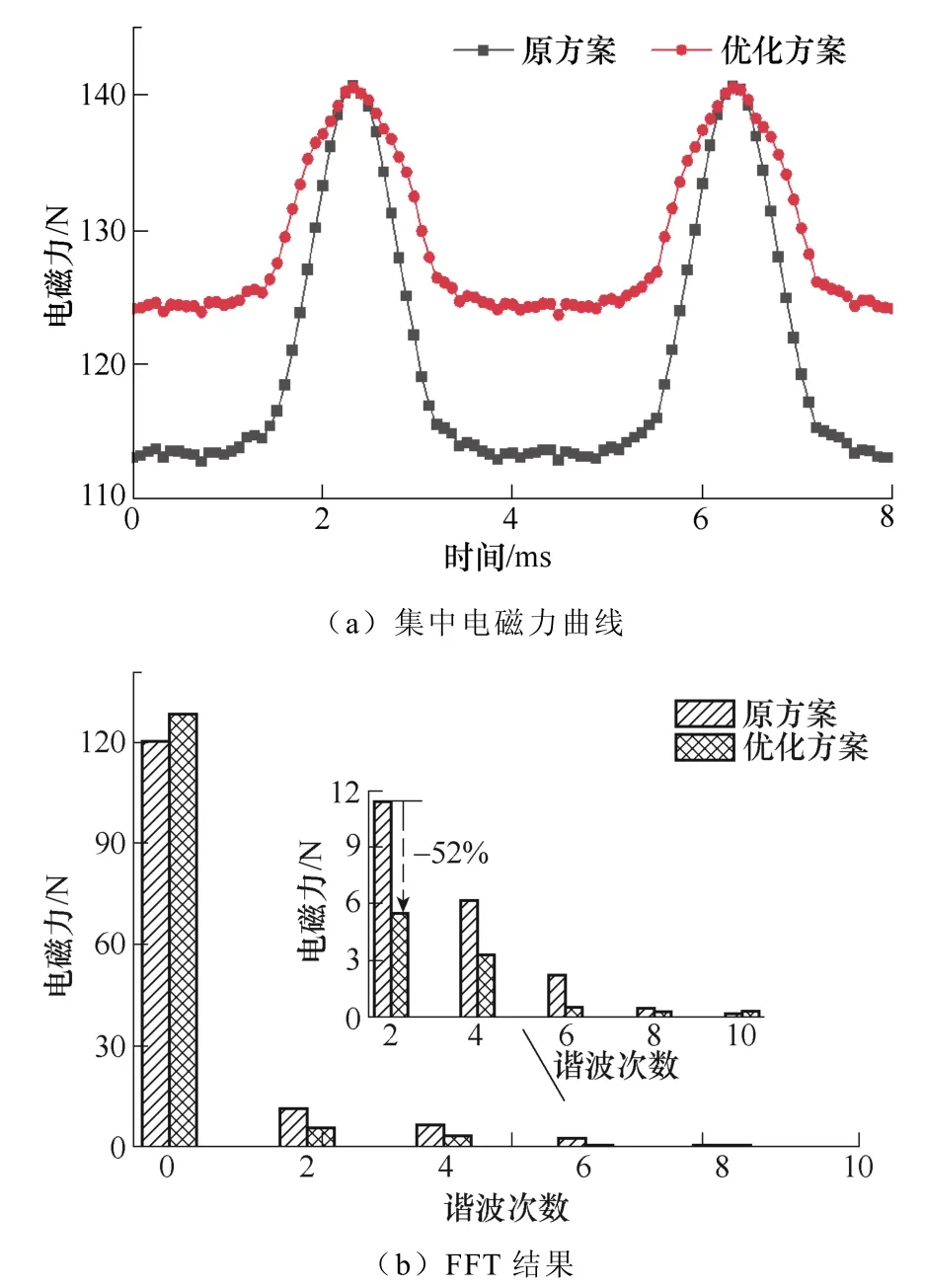
图12 原方案与优化方案集中电磁力对比Fig.12 The comparison of the concentrated force between the original scheme and the optimized scheme

分段交错不等磁极结构可使得磁极过零区域轴向偏移，电磁力密度波动幅度减小，从而达到削弱极频电磁力以及极频振动的目的。

3.3 优化前后电磁性能对比

局部切向电磁力会通过定子齿的杠杆效应引起径向振动，是重要的激振源[26]。因此，有必要分析优化方案对局部切向电磁力的影响。

优化前后，电机在空载时一对极下的切向电磁力密度分布曲线如图13 所示。可以看出，与原方案相比，优化方案切向电磁力密度峰峰值减小，降低约13.1 %。

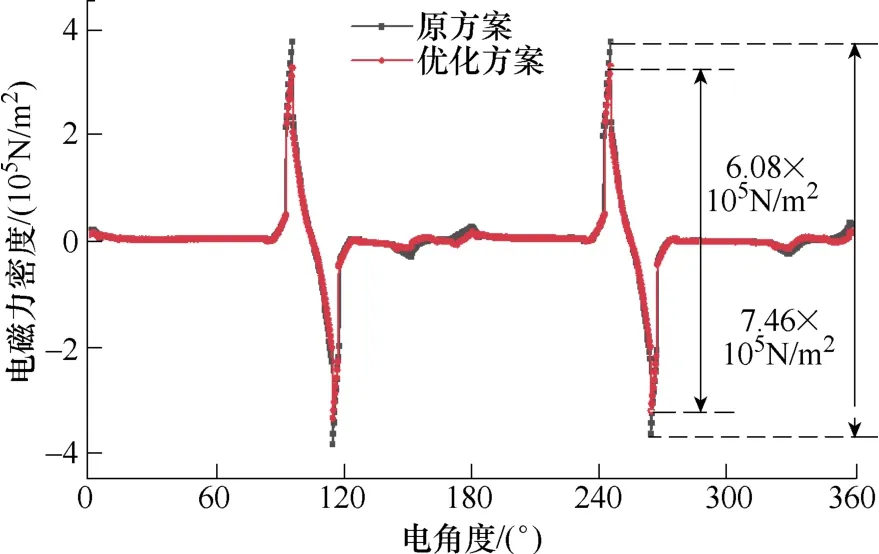
图13 切向电磁力密度曲线Fig.13 The curves of tangential electromagnetic force density

局部切向电磁力作用于单个定子齿，形成对单个齿的切向力矩。图14 为单个齿受到的切向力矩及其FFT 结果。可以看出，单个齿受到的切向力矩峰峰值由605 mN·m 下降至423 mN·m，降低约30 %。因此，优化方案对局部切向电磁力谐波具有较好的削弱作用。

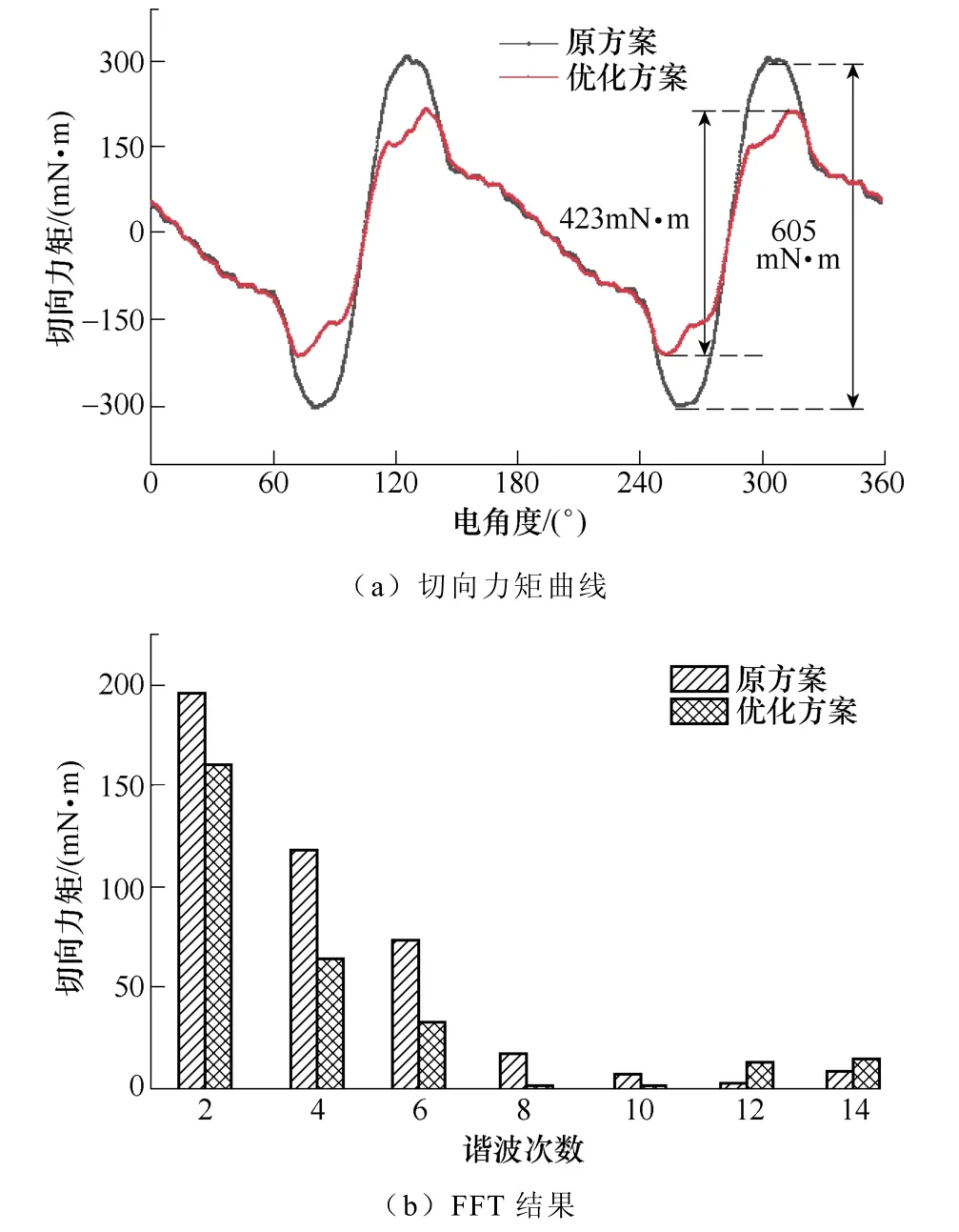
图14 单齿切向力矩及其FFTFig.14 The tangential moment and its FFT result

图15 为优化前后电机在额定负载工况下的转矩曲线，表3 对负载转矩的平均值进行对比。可以看出，优化前后平均转矩分别为4.21 N·m 与4.20 N·m，优化后平均转矩下降0.2 %，基本不变。因此，优化方案可有效保证电机的转矩密度。

表3 原方案与优化方案平均转矩对比Tab.3 The comparison of the average torque of the original scheme and the optimized scheme

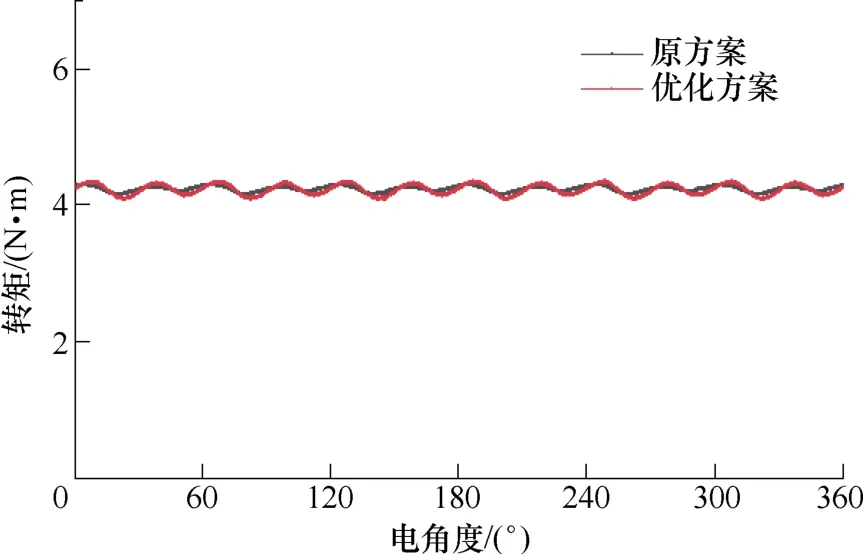
图15 转矩曲线Fig.15 The torque curves

4 电机振动噪声分析

4.1 模态分析

样机定子结构3D 有限元模型如图16 所示，主要包含定子、机壳、端盖。优化结构位于磁极区域，基本不影响定子模态。定子各阶模态振型及其固有频率如图17 所示。为清晰起见，隐藏机壳、端盖等结构，仅展示定子模态振型。

图16 样机定子模型Fig.16 The stator model of the prototype

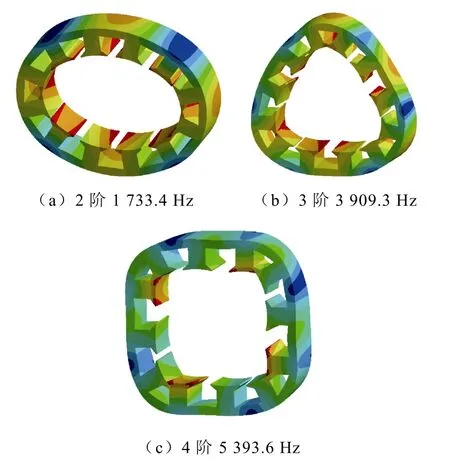
图17 样机定子模态振型Fig.17 The modal shape diagram of the stator

当电机特定阶次电磁力波某一频率分量等于或者接近定子相应模态固有模态频率时，定子会发生共振现象[26]。由图17 可知，额定工况下，低频范围内的定子各阶固有频率与相应电磁力频率相差较远，因此，共振现象不会发生。

4.2 振动响应分析

空载下优化前后样机的振动频谱仿真结果如图18 所示，可以看出，主要的频率点包括2f、4f、6f等 2f及其倍数频率点，这些频率点分别被称为一阶、二阶及三阶极频，其中2f处振动加速度幅值最大。优化前后，2f、4f、6f等关键频率的振动加速度幅值对比结果如图19 所示，与原方案相比，2f处振动加速度幅值由0.689 m/s2下降至0.341 m/s2，降低50.5 %，4f与6f处振动加速度幅值分别降低51.5 %、53.5 %。即一阶、二阶与三阶极频振动加速度幅值均明显降低，与电磁力谐波分析结果趋势一致。

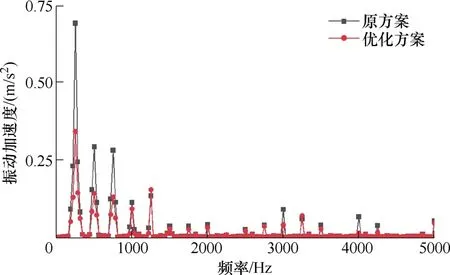
图18 空载下样机振动加速度频谱仿真结果对比Fig.18 The comparison of simulation results of vibration acceleration spectrum of the prototype under no-load condition

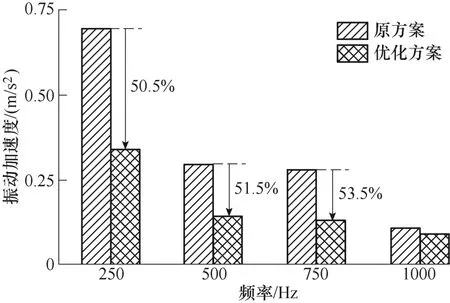
图19 空载下样机关键频率点振动加速度仿真结果对比Fig.19 The comparison of vibration acceleration simulation results of the prototype at main frequency points under no-load condition

负载下优化前后样机的振动频谱仿真结果如图20 所示，其中关键频率点的振动加速度被展示在图21。可以看出，与原方案相比，2f、4f、6f等关键频率的振动加速度幅值明显下降。因此，优化方案可有效削弱极频振动。

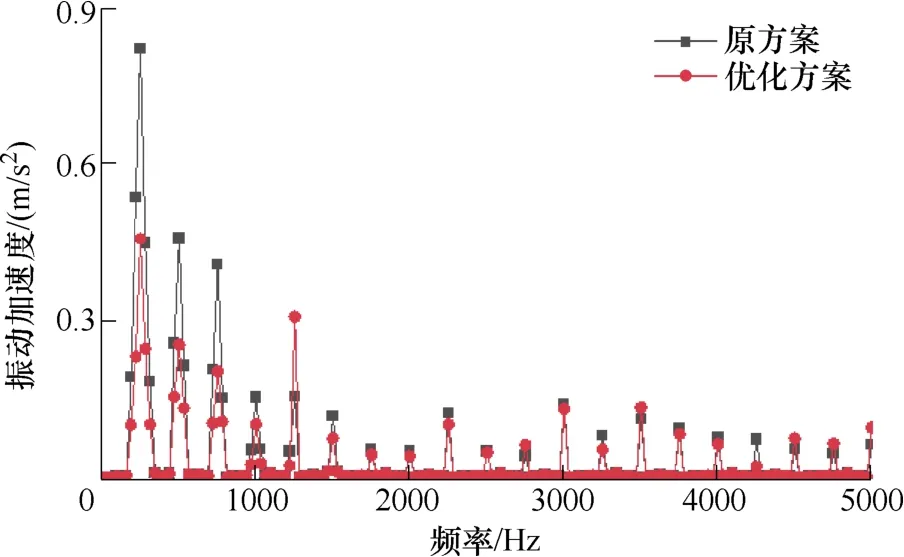
图20 负载下样机振动加速度频谱仿真结果对比Fig.20 The comparison of simulation results of vibration acceleration spectrum of the prototype under load condition

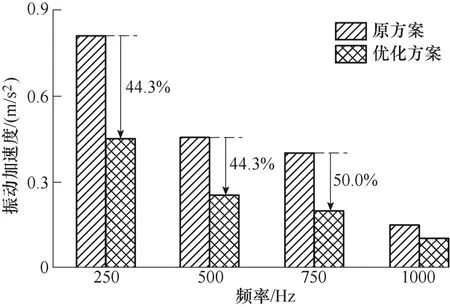
图21 负载下样机关键频率点振动加速度仿真结果对比Fig.21 The comparison of vibration acceleration simulation results of the prototype at main frequency points under load condition

5 振动实验

为了验证优化方案的有效性，本文对原样机与优化样机进行振动实验。原样机与优化样机转子结构分别如图22a 和图22b 所示。振动实验平台设置如图23 所示，主要包括：样机①及其控制板②、转矩传感器③、转矩测试分析仪④、磁粉制动器⑤、振动加速度传感器⑥以及数据采集器⑦。振动加速度的采集依靠DEWEsoft 公司生产的数据采集器与配套软件完成。电机在额定转速（1 500 r/min）运行。空载时，电机与磁粉制动器断开连接；负载时，调节磁粉制动器外加电压使其制动转矩达到额定转矩4.2 N·m，电机在额定负载下运行。由控制板显示屏可得到优化前后电机的相电流均为5.5 A，因此，优化方案基本不会影响电机的转矩密度。

图22 两台样机的转子结构Fig.22 The rotor structures of the two prototypes

图23 样机振动测试实验Fig.23 The vibration test experiment of the prototype

额定转速下，空载时优化前后样机的振动加速度实验结果如图24 所示。可以看出，两台样机的振动加速度峰值频率均在2f及其倍数频率处，其中，2f处振动加速度幅值最大，因此，振动仿真结果频谱分布规律与实验结果基本一致。与原样机相比，优化方案在2f、4f与6f三个频率点振动加速度峰值明显下降，其中2f处振动加速度幅值由0.658 m/s2下降至0.309 m/s2，降低53 %，与仿真结果变化趋势基本一致。

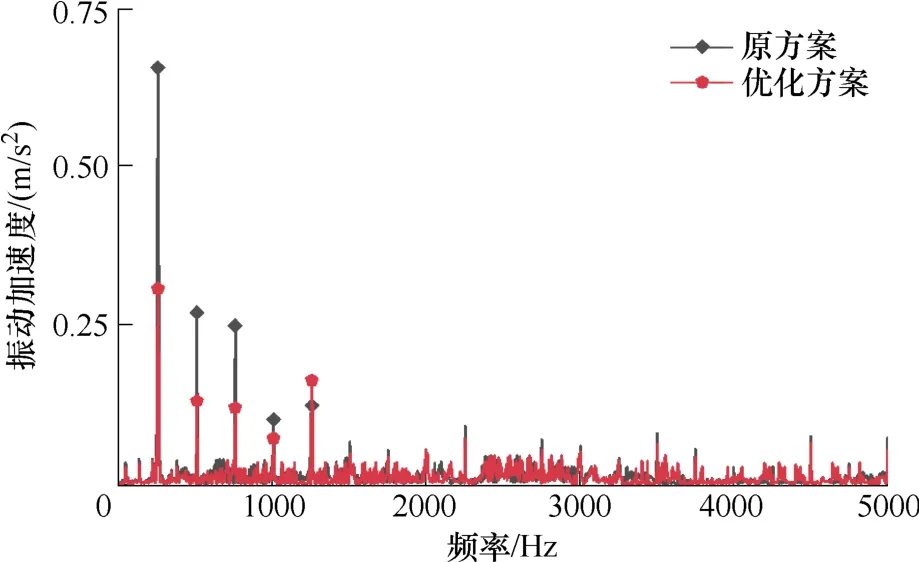
图24 空载下样机振动加速度频谱实验结果对比Fig.24 The comparison of experimental results of vibration acceleration spectrum of the prototype under no-load condition

额定转速下，负载时优化前后样机的振动加速度实验结果如图25 所示。可以看出，与原样机相比，优化方案在2f、4f与6f三个频率点振动加速度峰值明显下降，与空载工况变化趋势基本一致。因此，优化方案可有效削弱极频振动。

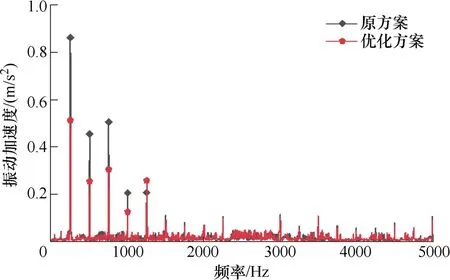
图25 负载下样机振动加速度频谱实验结果对比Fig.25 The comparison of experimental results of vibration acceleration spectrum of the prototype under load condition

6 结论

针对永磁电机极频振动，本文提出了一种分段交错不等磁极的削弱方法，并通过优化前后的样机实验验证了优化方案的有效性。所得结论可以为表贴式永磁电机极频振动的削弱提供有价值的参考。

1）磁极交替区域存在磁通密度过零点，该位置处电磁力密度大幅度波动；当磁通密度过零区域经过定子齿部时，大幅度波动的电磁力密度经过积分，导致齿部集中力在峰值与波谷之间振荡，从而引起了极频电磁力谐波以及极频振动。

2）分段交错不等磁极结构主要通过调制磁极过零区域轴向偏移，减小电磁力密度波动幅度，来削弱极频电磁力以及极频振动；此外，该结构基本不影响平均转矩，可以有效保证电机的转矩密度。