基于FastICA的无人机声学检测方法*
王文帅,樊宽刚,别 同
(1.江西理工大学 机电工程学院,江西 赣州 341000;2.江西理工大学 电气工程与自动化学院,江西 赣州 341000;3.江西省磁悬浮技术重点实验室,江西 赣州 341000)
0 引 言
近年来,无人机(unmanned aerial vehicle,UAV)迅猛发展,在航空测绘、农业植保、航空摄影、物流运输、管线巡检、大气监测、应急救援等领域发挥重要作用。同时,无人机被用于走私、恐怖袭击、扰航、侵犯隐私等的负面报道层出不穷[1~3]。因此,为了有效应对无人机发展带来的挑战,发展无人机检测与反制技术迫在眉睫。
目前,无人机检测领域发展较快,已取得一定进展。文献[4]针对低慢小的低空目标,构建了低空目标雷达回波模型,最后结合Radon变换实现无人机的雷达检测。文献[5]讨论了基于遥控射频信号特性识别无人机的方法。该方法利用机器学习(machine learning,ML)技术分析典型无人机遥控信号发射机发送给无人机的无线电控制信号,实现对无人机进行检测。文献[6]提出了一种基于WiFi指纹的无人机检测方法,主要通过对无线通信量进行统计指纹分析来检测附近的无人机。文献[7]提出了一种利用城市监控网络识别无人机的方法,该方法基于深度学习算法进行无人机检测。文献[8]采用基于黑体校正的双波段法对飞行中的无人机目标辐射特性进行测量,对飞行状态下的无人机目标的温度进行了反演,为无人机的夜间识别提供数据支撑。文献[9]提出了一种基于卷积神经网络的声音识别无人机的方法,识别无人机的准确率为96.5 %。文献[10]提出了基于ML框架的无人机检测和分类方法。该方法采用Mel频率倒谱系数(Mel frequency cepstrum coefficient,MFCC)和线性预测倒谱系数(linear prediction cepstrum coefficient,LPCC)提取无人机特征,实验结果表明,该方法无人机检测准确率最高可达96.7 %。
从发展现状来看,无人机检测技术主要可分为雷达检测、射频信号检测、光电检测、声学检测等手段。整体来看,这些无人机检测手段各有利弊。雷达检测技术主要是通过多普勒效应进行检测,具有识别距离远、技术发展成熟、不受天气影响等优点。然而,针对多旋翼无人机这类“低小慢”目标,雷达技术将难以发挥作用。射频信号检测技术能够对无人机类型进行识别,较为隐蔽,但在城市的复杂电磁环境下,识别率将大大降低。光电检测技术主要分为可见光与红外检测,依托于人工智能的迅猛发展,可实现无人机的精确识别与跟踪,但在恶劣的天气中,检测效果较差。声学检测技术具有成本低、不会被遮挡的优点,但是存在识别距离较近、易受噪声干扰以及技术发展不成熟的缺点。综合各种检测技术的特点分析来看,无人机检测技术必将朝着集成化发展。将多种无人机检测技术集成到一个综合的反无人机平台中,是未来无人机检测技术发展趋势[11]。而声学检测作为无人机检测技术的重要组成部分,仍存在技术成熟度低、抗干扰性差等问题。因此,亟需针对无人机声音检测技术进行研究。
当前国内外的研究主要集中于直接对无人机的声音进行分析,未能与声音抗干扰算法进行结合,且目前针对强干扰环境的无人机声学检测研究较少。针对这一问题,本文提出基于快速不动点迭代的独立成分分析(fast independent component analysis,FastICA)算法实现强干扰环境下的无人机声音提取与识别。为了验证方法的有效性,本文实现了强干扰环境的无人机检测以及不同距离无人机检测,并使用不同的无人机对算法可靠性进行验证。实验结果证明了基于FastICA算法的无人机声学检测方法,可大大提高强干扰环境下的无人机识别率。
1 无人机声学识别模型
1.1 盲源分离模型
盲源分离(blind source separation,BSS)通常可以表述为从一组观测信号中,提取出源信号的过程。由于除了观测信号,混合过程和源信号都是未知的,因此,称之为“盲”分离[12]。盲源分离问题通常可以由鸡尾酒会问题形象的阐述:假定在一场酒会上有n个声源,使用分布于不同位置的n个麦克风将这些声音记录下来,将获得n个观测信号。假定混合是线性的,盲源分离模型可以表述为
X=A×S
(1)
式中X为观测信号,A为混合矩阵,S为源信号。
如果能获得一个解混矩阵W,将源信号重构,则盲源分离问题得到解决
(2)
式中W为解混矩阵,为源信号的重构。
基于盲源分离模型,可想到,如果将无人机声音以及环境干扰声音均视作源信号,在较近距离内,可忽略声音传播的延时,则声音的混合可近似为一个线性过程。因此,可利用盲源分离算法解决强干扰的无人机声音识别问题,具体如图1所示。
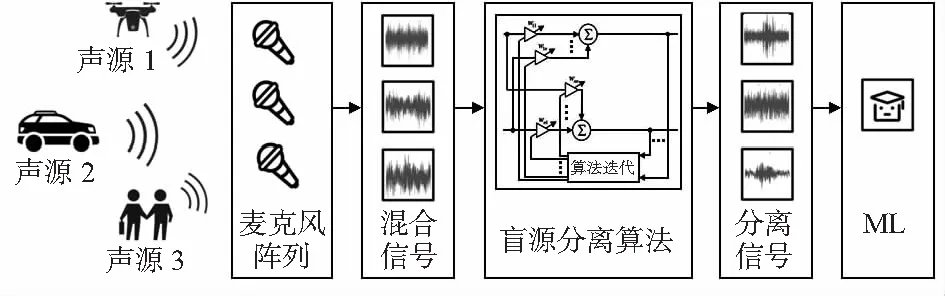
图1 算法流程
1.2 独立成分分析算法
根据盲源分离模型,只要求得分离矩阵W,盲源分离问题就将得到解决。独立成分分析(independent component analysis,ICA)算法实质上就是寻求一个使观测信号线性组合独立性极大化的分离矩阵。当线性组合的独立性达到最大时,对应的观测信号的线性组合可被认为是分离的“源信号”。
为了评价观测信号线性组合的独立性,ICA算法需要设定一个目标函数。通过最大化目标函数来求解ICA问题。常用的ICA目标函数包括极大化非高斯性的ICA、基于极大似然估计的ICA、极小化互信息的ICA、基于张量的ICA、非线性去相关的ICA等[13]。本文选取极大化非高斯性ICA方法中的负熵作为衡量独立性的目标函数。负熵的定义为
(3)
式中J(y)为y的负熵,ygauss为与y同相关矩阵的高斯随机变量,H(y)为y的微分熵,py为y的分布函数。
由微分熵的定义可知,y的负熵小于等于0,当且仅当y为高斯随机变量时,等号成立。使用负熵作为非高斯的度量优势在于其具有严格的统计意义以及良好的鲁棒性。但负熵的最大问题在于负熵的计算是十分困难的,因此,在实际应用中,需要一种负熵的简化定义。实践中负熵的计算可简化为
J(y)∝(E{G(y)}-E{G(v)})2
(4)
式中v为零均值单位化的高斯随机变量,G为任意的实际非二次函数,E为期望。实践中,较为有效的经验公式为
(5)
式中 常数a1取1≤a1≤2,通常取1。
接着,需要对目标函数求极值,以便获得极大化的非高斯解。本文采用基于快速不动点迭代的负熵极大化ICA算法。基于快速不动点迭代的ICA算法通常称为FastICA。FastICA在大部分情况下可获得立方阶次的收敛速度,同时,不需要额外考虑学习速度等参数的设置,因此,具有迭代速度快且简单易用的优点。
使用不动点算法首先需要选择恰当的非线性函数g,即式(5)中函数G的导数。接着需要对观测信号进行预处理,主要包括中心化和白化。中心化需要使观测信号均值为零;白化则是使白化的观测信号的协方差矩阵为单位对角阵。如假定中心化的观测信号为x,白化后的观测信号为z。令Cx=E{xxT}(T代表矩阵转置),对协方差矩阵Cx进行特征分解有Cx=QΣQ-1,则白化过程如式(6)所示
z=Σ-1/2QTx
(6)
在预处理后,FastICA依据式(7)进行迭代,每次迭代后要进行标准化,以消除迭代向量长度对目标函数影响
w=E{zg(wTz)}-E{g′(wTz)}w
(7)
式中g′为g导数。
FastICA算法的主要流程如下:1)数据预处理,获得z;2)随机选取具有单位范数的向量w;3)迭代:w=E{zg(wTz)}-E{g′(wTz)}w;4)令w=w/‖w‖;5)如收敛,则结束;未收敛,则返回步骤3。
2 实验验证
2.1 数据与实验条件
本文使用的数据来源于两部分。干扰声音来源于开源噪声库NoiseX—92[14],从中共选取了6种声音对无人机声音进行干扰。实验在相对安静的傍晚使用了2种大小不同的多旋翼无人机,进行无人机声音录制,以验证本文方法对不同无人机的识别性能,具体如图2所示。为了便于分析,使用Audition将干扰声音与无人机声音参数统一,设置为48 kHz,16位量化位数、单通道。实验使用MATLAB 2020a进行数据处理与分析。

图2 实验使用无人机
每种无人机悬停在1 m的高度进行声音录制,每段声音长度为30 s。为了验证本文方法在不同距离下的无人机识别结果,分别录制了DJI Phantom 4 Pro悬停状态下距离为1~20 m的无人机声音,每隔1 m进行一次录制,每段声音长度均为30 s。实验时,将数据集划分为测试集与训练集,比例为4︰1。
ICA模型的混合矩阵A为n×n的随机矩阵,n取决于混合信号的个数。每个试验均重复50次,将识别结果取均值,防止混合矩阵的特殊取值对实验结果产生干扰。本文选择MFCC进行特征提取,由于并不是针对人声进行识别,因此,不需要使用预加重对高频部分进行增强。使用汉明窗进行分帧,窗长设置为20 ms;帧间隔为480;每帧进行960点FFT。由于本文实验中的数据集并不是大规模数据集(最多时约40 000个样本),因此,选择易于理解和实现简单的决策树分类器进行无人机的识别。
实验使用识别率η来评价算法性能,其定义为
(8)
式中 TP为正确识别的特征,ALL为特征总数。
2.2 不同信源数混合的无人机识别
为检验本文算法抗干扰的能力以及对不同无人机的识别能力。将2种无人机声音分别与不同数目的干扰声源使用随机矩阵混合,接着使用FsatICA算法提取无人机声音,并对混合无人机声音以及本文算法分离的无人机声音进行识别,识别结果如图3所示。从图3可以看到,在信源数目较少时,2种无人机的混合声音识别率在50 %以上,而随着信源数目的增加,无人机声音受到的干扰越来越大,因此,2种无人机混合声音的识别结果均呈现下降趋势。而通过本文方法进行无人机声音提取后,2种无人机的识别率接近100 %,基本不受信源数目的影响,相较混合信号,识别效果有了较大提升。

图3 混合不同信号数识别结果
2.3 不同距离无人机识别
为测试距离因素对本文算法的影响,将1~20 m的无人机声音与2种干扰噪声混合,再使用本文算法提取无人机声音。本文首先对不同距离下无人机的能量衰减情况进行分析,无人机声音能量Ps的计算由式(9)给出
Ps=10×lg(S2)
(9)
式中S为无人机声音信号。
图4(a)展示了距离分别为1,6,11,16,20 m无人机声音能量随时间的分布情况。图4(b)展示了无人机声音能量随着距离的衰减。从结果中可以看到,每个距离段的无人机能量比较稳定,基本不随时间变化。但随着距离变远,无人机声音能量快速衰减。
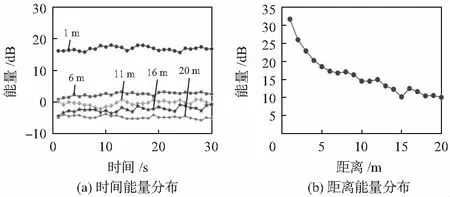
图4 无人机能量分布
图5展示了不同距离的无人机识别情况,可以看到,随着距离增大,无人机能量衰减,导致带有干扰的无人机声音识别率逐渐降低至约10 %。而使用本文方法对带有干扰的无人机声音进行提取后,识别率较为稳定,在10 m内接近100 %,在10 m外识别率开始波动,但依然稳定在90 %以上。

图5 不同距离的无人机识别
3 结 论
本文针对多声源干扰环境下的无人机声音识别问题,提出一种基于FastICA的无人机识别方法,解决了强干扰环境无人机声音识别问题。本文将不同型号的无人机声音与多种干扰声音进行混合,然后使用FastICA算法从混合信号内提取无人机声音用于识别,从而提高了识别率。实验结果表明:本文所述方法在多种声源混合的情况下仍能较好地识别无人机声音,同时对不同型号的无人机均具有较好地识别效果。同时考虑了识别距离对识别率的影响,结果表明,随着距离衰减,本文算法仍能较好地识别无人机。但在更远的范围内无人机声音识别问题本文尚未进行讨论。未来考虑基于WSNs技术搭建无人机声音传感器识别网络,实现较大范围的无人机声音识别。

