基于渐进式神经网络的六足机器人避障策略迁移*

董星宇，傅汇乔，王鑫鹏，唐开强，留沧海

(1.西南科技大学 制造科学与工程学院，四川 绵阳 621000；2.南京大学 工程管理学院 控制与系统工程系，江苏 南京 210093；3.制造过程测试技术省部共建教育部重点实验室，四川 绵阳 621000)

0 引 言

深度强化学习为机器人控制提供了新的方法，特别是对于多足机器人，如何高效地通过非结构地形这种复杂的任务，深度强化学习算法能够进行有效的控制[1]。目前算法主要应用在机器人路径规划与运动控制方面，仅仅局限于仿真器中的实现，在实际的环境下算法的可行性、准确性还没有得到过验证，但是在现实环境中对算法进行验证时，六足机器人与环境进行交互、采样时，会出现采样效率太低和避障任务中由于碰撞造成的不可逆损伤等问题[2,3]。而利用渐进式神经网络(progressive neural network,PNN)在仿真器中实现跨环境的迁移训练，并将训练后的模型植入样机中进行现实环境的避障测试是一种解决该问题的方法。PNN是由Rabinowitz N C等人[4]提出的一种新结构的神经网络，相比于参数精调(fine-tune)方法可能丢失已学习到的预训练模型特征的问题，即“灾难性遗忘现象”，PNN将已经训练好的模型保存到模型池中，并且在新的训练任务中保持它的权重不变，训练过程中，通过侧向连接来提取已有模型的权重参数，避免了这种现象的出现。国内外专家已经将迁移强化学习成功应用在工业机械臂、轮式机器人、四足机器人、水下机器人等机器人的技能学习，六足机器人的应用相对较少[5]。Rusu A A等人[6]提出使用PNN来弥补从仿真迁移到现实环境的差距，通过该方法，证明了深度强化学习可以用于实现机器人的快速策略学习。隋洪建等人[7]提出使用PNN可以有效减少学习目标任务所需要的时间。Peng X B等人[8]提出利用PNN来减少现实与仿真环境的差距。

本文采用一种双重深度强化学习(Double deep Q-network,Double-DQN)与PNN相结合的算法。首先，搭建初始避障环境，并通过Double-DQN训练一个避障模型；其次，在仿真环境中搭建更为复杂的环境，通过将初始环境中训练的模型作为目标环境的预训练模型，并在预训练模型与当前任务模型之间采用横向连接方式进行数据传输；最后，将搭建的模型在目标环境中训练，并植入样机系统中进行现实环境的避障测试。实验表明：该方法可以有效减少六足机器人在目标环境中学习避障任务所需的时间。

1 多类型障碍物环境搭建

1.1 六足机器人样机避障能力分析

足端工作空间范围代表了六足机器人腿部可活动范围，腿部工作空间的范围大小会影响机器人避障能力。为了搭建出六足机器人可通行的避障环境，对于足端的工作空间分析是不可或缺的任务[9]。足端工作区间与腿部扭转角、关节转动角度范围、大腿和小腿杆长和偏移量有关[10]。为避免六足机器人在运动过程中相邻腿之间发生干涉，本文中六足机器人设定的关节角范围：基节θ1为[-45°,45°]；髋关节θ2为[0°,45°]；膝关节θ3为[-135°,-90°]。

本文通过MATLAB的Robotics工具箱对六足机器人单腿模型进行仿真。六足机器人腿部基节为68 mm，大腿为104 mm，小腿为185 mm。根据关节转角的约束条件和运动学关系，解算并仿真出足端三维点云图和平面图。如图1所示。图中的X轴、Y轴、Z轴分别为六足机器人的左右、前进、高度方向。以机器人重心为原点，向上为Z轴正方向，向下为Z轴负方向。分析图1可得，机器人腿部的三维动作空间，从图1(b)的X-O-Y平面投影可知，六足机器人足端工作空间在该平面的投影形状近似为扇形，其外径270 mm与内径30 mm则为足端点最远与最近的投影点集合。从图1(c)中可得出，足端点最高位置约为-50 mm，最低位置约-180 mm；从图1(d)中可知，在前进方向上足端点投影最大值可约达200 mm。

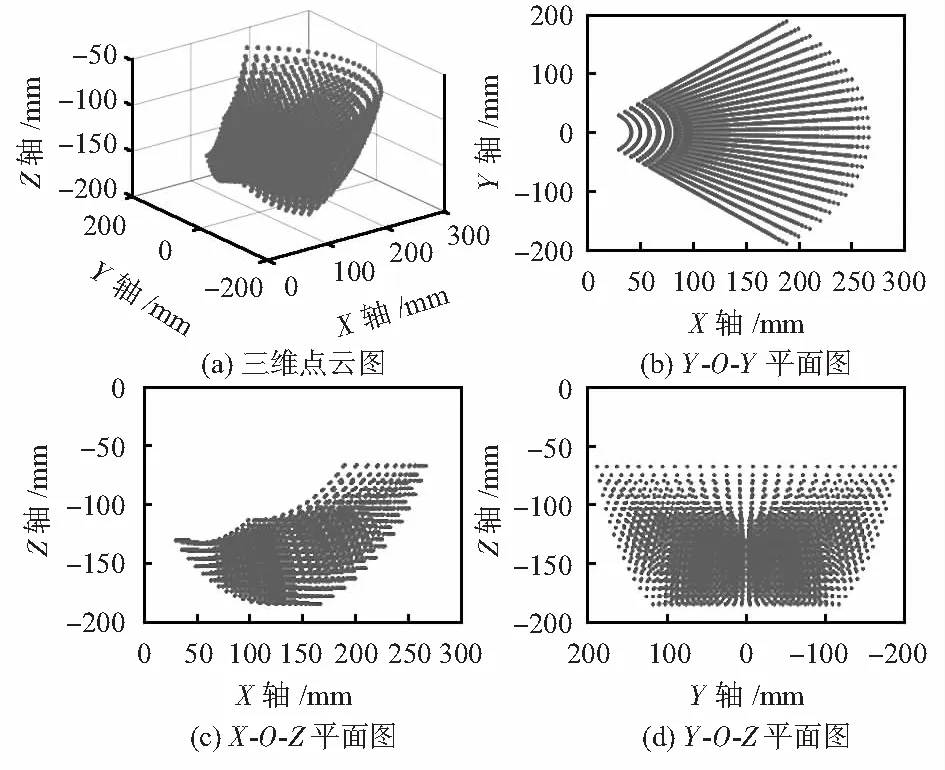
图1 足端三维点云图和平面图

1.2 避障实验环境搭建

六足机器人进行避障的环境设计准则为：障碍物尺寸应设置在六足机器人运动能力范围内，并且设计尺寸不应该为六足机器人运动极限位置，且应该设置在六足机器人运动极限位置之间来防止测试时六足机器人与障碍物发生碰撞损伤；为保证模型的训练速度，防止迭代时间过长，避障环境的尺寸范围不应过大，且障碍物分布应该尽量均匀[11]。为此，对机器人避障环境进行设计。六足机器人避障环境总体尺寸设计为360 cm×300 cm。障碍物类型共有4种，分别为长、宽、高为100 cm×90 cm×14 cm的台阶；长、宽、高为90 cm×30 cm×27 cm的隧道；沿轨迹行进的巡检小车，巡检速度恒定且巡检轨迹为往返370 cm的直线；高度为40 cm的围墙和长、宽、高为200 cm×40 cm×40 cm长方形障碍物。根据设计的避障任务在Unity仿真器中进行避障环境搭建，如图2所示。

图2 仿真器中的避障环境

2 深度强化学习算法

2.1 强化学习

强化学习为一种标记延迟的监督学习，其根据外界环境的反馈学习到一套行动策略，帮助智能体取最大化的预期奖励目标。强化学习的过程将通过马尔科夫决策过程来表示，而六足机器人的避障问题可以视为一个马尔科夫决策过程，机器人下一时刻可能面对的场景只与当前所处场景和状态转移方程相关，与机器人过去经历的历史状态无关[12,13]。

状态、动作、状态转移方程和回报函数为马尔科夫决策过程中的4个主要元素。通过当前时刻的状态，决策出下一时刻的动作，再根据输出动作和状态，经过状态转移方程，就能够得到下一个时刻智能体所处的状态，并遵循奖惩函数的计算，获得此次状态转移的回报。

在马尔科夫决策过程中需要通过值函数来评价某个决策过程中获得的总的回报。当前时刻后的所有回报的值函数可分表示为

(1)

式中γ为折合系数，γ≤1，V(s)为值函数的值。

进而推出贝尔曼方程

V(s)=E(r0+γ·V(st+1)|s=st)

(2)

式中γ·V(st+1)为未来回报，r0为当前回报。γ越小，表示算法越希望智能体当前所获得的回报值最大。

根据贝尔曼方程，当智能体处于某一状态时，让其采取能够使当前回报和未来回报之和最大化的动作，用贝尔曼最优方程表示如下

a(s)=maxa∈AE(r0+γ·V(st+1)|s=st)

(3)

2.2 双重深度强化学习模型

深度强化学习结合了深度学习的感知能力和强化学习的决策能力，智能体在环境中输入的状态经过神经网络编码之后映射成离散的Q值，每个Q值对应一个动作，并根据贝尔曼最优方程来选取执行动作，然后通过反向传播(back propagation，BP)来更新神经网络的参数[14]。本文采用Double-DQN算法训练六足机器人避障模型，算法通过解耦目标Q值动作的选择和目标Q值的计算来消除过度估计的问题和使用经验回放来避免训练数据的相关性[15]。通过实际动作价值Q网络在现实中训练参数，迭代C次后将权重复制更新到目标动作价值Q网络中以降低过估计对训练结果的影响。Double-DQN的目标Q值定义如下

Qtagret=r+γQ(s′,argmaxaQ(s′,a|w)|w′)

(4)

式中γ为折扣因子，w为Q现实中网络结构权重，w′为Q估计中网络结构权重,s′为下一时刻感知的环境状态，a为选择的动作，r为奖惩回报值。

本文的网络结构主要是由长短期记忆(long short-term memory,LSTM)层和2层全连接层构成。六足机器人在某一状态时，测距模块采集得到的数据经过预处理后，通过LSTM层将障碍物数据变为长度固定的编码向量，然后将机器人自身状态信息同障碍物信息合并输入全连接层处理。最终网络输出设计的离散动作对应的Q值。

3 PNN结构

PNN是一种适用于机器人控制领域从仿真到现实的迁移方法[6]，PNN可以将模型在源任务中学到的特征迁移学习到目标任务中，而不会出现Finetune方法应用到机器人控制策略时，特征提取层从源任务中学习到的知识出现灾难性遗忘，导致经验迁移的效率发生显著下降的情况。仿真环境与真实环境间存在较大的现实误差，当模型从仿真迁移到现实中时，采用PNN能够给模型每层增加新的输入连接，相当于增大了模型网络的容量，有助于弥合现实误差。

图3 PNN示意

(5)

4 实验结果与分析

4.1 实验平台搭建

本文搭建的六足机器人避障控制系统结构如图4所示。六足机器人样机的避障控制架构由感知系统、决策系统和执行机构3个部分构成。计算能力强的PC作为决策系统，用于处理算法运算和训练避障策略，通过无线通信模块将上层运算处理得到的指令发送给下位机。下位机主控为STM32F4单片机，单片机得到指令后，将控制由舵机构成的执行机构，使样机动作，并协调控制激光测距传感器、六轴加速度传感器组成的感知系统采集样机在环境中的状态信息，最后下位机再通过WiFi模块将采集得到的信息反馈给上位机处理。控制系统将循环以上操作直至目标任务结束。

图4 控制系统结构

本文基于PNN的迁移实验将完成如表2所示的3个实验内容。

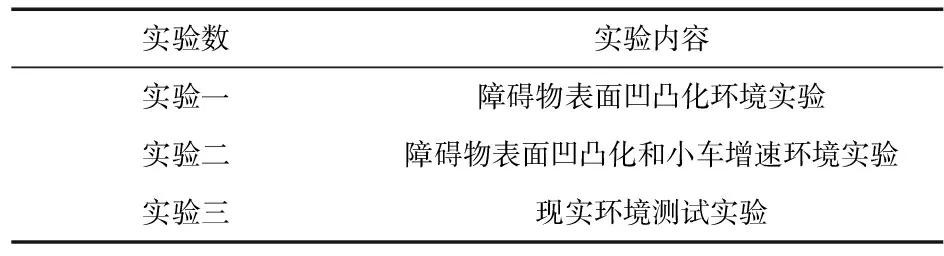
表2 PNN实验任务

实验一和实验二将在Unity仿真器中通过提高四驱小车的速度和将障碍物的表面随机凹凸处理来改变环境复杂性，并分别采用PNN结构搭建的模型和无PNN结构搭建的模型来训练六足机器人避障。实验中PNN结构的预训练模型网络参数将会被冻结，不会因为反向传播而更新。实验中无PNN结构搭建的模型方法有2种：1)采用Finetune将训练模型的参数作为新搭建模型中前2层的初始参数；2)新搭建的模型中前2层的参数值随机初始化，该方法本文称为Rand。实验一和实验二最终将对比3种模型训练六足机器人在避障环境中获得的回报曲线。实验三将实验一和实验二中训练的模型作为PNN的初始列在仿真环境中训练后迁移进六足机器人样机中进行测试，对比并总结六足机器人在仿真环境和现实环境中避障测试的表现。实验中采用的模型结构如图5所示。

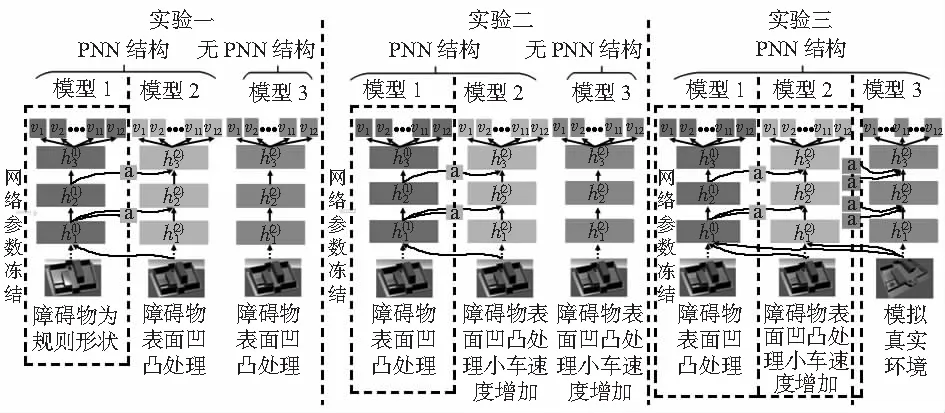
图5 实验中采用的模型结构

4.2 障碍物表面凹凸化环境实验

实验一将前文构建的环境障碍物表面随机凹凸化处理，凹凸表面的随机误差在±20 mm之间，障碍物表面随机凹凸化处理后的环境相较于规则形状的障碍物环境，更贴合真实环境。实验一环境中动态障碍物四驱小车沿轨迹行进的速为14 cm/s，仿真环境中六足机器人行进速度为8.6 cm/s，加速行进速度为16 cm/s。

避障环境中完成目标任务300次后的奖惩值对比，由图6中回报曲线可以看出PNN比Finetune和Rand对目标任务的学习更加迅速，提高了六足机器人在实验一避障环境中学习完成目标任务的效率，说明了PNN在对源任务和目标任务之间的经验迁移是成功的。

图6 实验一中各模型测试的回报值对比

4.3 障碍物表面凹凸化环境加小车增速实验

实验二将延续采用实验一构建的障碍物表面随机凹凸化处理的环境，并将四驱小车沿轨迹行进的速度提高为20 cm/s。六足机器人行进速度和加速行进速度与实验一一致。该实验小车的巡检速度大于六足机器人加速行进的速度，若六足机器人仍采用实验一训练得到的避障策略必然会与小车发生碰撞。

图7为3种模型训练六足机器人在实验二的避障环境中完成目标任务300次后的回报值对比，由图看出，PNN仍比另外2种模型的学习效率高。而在该环境中采用Finetune的收敛速度慢于Rand，是因为Finetune在进行目标任务的训练时，源任务模型部分有效参数被梯度更新所覆盖，从而导致灾难性的遗忘现象发生。而在PNN的迁移方法中，因前列网络参数被冻结，不会在训练中发生改变，所以可以有效防止遗忘现象的发生。实验一和实验二的训练结果证明了PNN用于机器人执行动作空间相似，但环境存在差异的场景中能够有效提高六足机器人的学习效率。

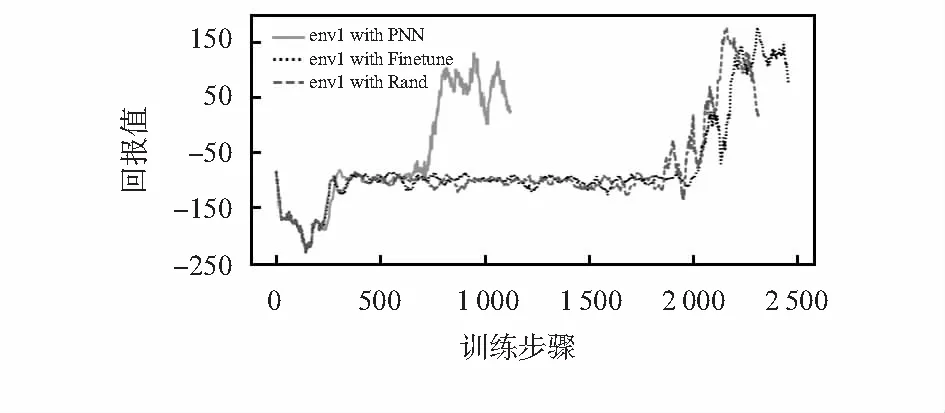
图7 实验二中各模型测试的回报值对比

4.4 PNN现实环境测试实验

实验三在仿真器中搭建与实验一和实验二不同的避障环境如图8(a)所示。在该环境中，六足机器人常速行进速度为8.6 cm/s，加速行进速度为16 cm/s，四驱轨迹小车移动平均速度约为24 cm/s，抵达轨迹端点处小车停顿和转向间隔时间共计为15 s。并在现实中搭建避障环境，如图8(b)所示。

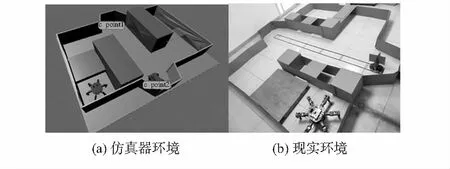
图8 实验三的环境

在仿真环境中，采用PNN训练六足机器人完成避障任务，并将训练后的模型植入样机的避障控制系统中，攀爬动作和匍匐动作为设定的离散动作，在执行该动作的过程中上位机将不会处理感知系统接收的信息，当动作执行完毕后再返回六足机器人的状态信息到上位机中处理。实验三的六足机器人避障测试效果如图9所示。图中六足机器人各状态的时序不连续，在状态1时，六足机器人由初始位置执行常速向前运动，四驱小车沿箭头向前行驶；在状态2时，六足机器人检测到台阶并开始执行攀爬动作；在状态3时，六足机器人将完成攀爬动作；在状态4时，六足机器人检测到有动态障碍物时采取加速向左运动躲避；在状态5时，六足机器人采取加速向后运动和加速向右运动通过四驱小车巡检轨迹路段，四驱小车此时正执行等待转向动作；在状态6时，六足机器人检测到前方的隧道障碍并执行匍匐动作；在状态7时，六足机器人执行完匍匐动作并顺利通过隧道；在状态8时，六足机器人抵达目标位置，成功完成动态避障任务。

图9 实验三的六足机器人避障测试效果

5 结 论

本文采用PNN结构与Double-DQN算法相结合的方法来克服深度强化学习应用在六足机器人避障学习效率低下的问题，提出一种跨环境经验迁移模型来提高六足机器人从源任务中学习避障策略的效率。通过在仿真器中搭建2种更为复杂的环境来评估本文提出的PNN模型，实验结果表明：该模型成功地令六足机器人在目标环境中更有效的学习到避障策略。并且，通过将仿真器中训练的模型迁移到六足机器人样机中测试，因为仿真环境与真实环境存在现实误差，会导致样机出现避障失败的情况，但样机能够成功完成目标任务，证明本文提出的基于PNN的避障模型具有可行性。