基于费兹定律变导纳控制的手术机器人人机交互

陆玮铭, 胡 陟, 王泽华, 倪双涛

(上海工程技术大学 电子电气工程学院,上海 201620)

0 引 言

近年来，对医疗机器人的研究受到了越来越多研究人员的关注，其中，对使用机器人来协助医生完成手术又是医疗机器人技术领域中的研究热点。颅颌面部外科手术是一项复杂程度和危险性较高的外科手术，将医疗机器人技术引入到颌面部外科手术之中，能够大幅度提高手术的稳定性、精确性[1]。在机器人辅助手术操作过程中，医生快速拖动机器人末端从初始位置移动至手术区域位置内的移动过程是大范围的点到点移动操作，由于手术空间的复杂性，不仅需要保证拖动过程的快速平稳，过程中的安全性也是需要解决的难题[2]。

与其他机器人相比，手术机器人有其不同特点和控制要求，其性能必须满足对个体差异和环境变化的适应性、人机交互的柔顺性、面对异常情况的安全性等要求，从而对控制系统的准确性、可靠性、智能化水平等都提出更高的要求。为了解决这个问题，越来越多的研究者开始关注基于导纳或阻抗控制的人机交互控制。段星光等人[3]提出了一种基于速度控制的方法来研究人机协同交互问题。杜志江等人[4]通过在线学习将人的操作特性考虑到交互过程之中，根据操作者自适应地调整导纳参数。王应健等人[5]采集检测人体上肢力信息，利用运动意图检测提高人机交互的自然性。Tsumugiwa T等人[5，6]以人机间作用力的微分形式估计人手臂刚度并以此修改虚拟阻尼值。

手术机器人协同控制中比较常用的导纳控制可以建立机器人的力与位移/速度的动态关系，使用导纳控制对机械臂进行操作时，力与速度之间呈正相关关系，施加力大则速度快，力小则速度慢，更加符合操作习惯。单纯的导纳控制难以解决人机协同控制中强非线性、时变性以及干扰等问题，若导纳控制参数能根据任务和环境的变化进行动态规划调整，则控制性能将会明显提升。保罗·费茨受到信息论的启发，对人类操作过程中的运动时间、范围和准确性进行研究，提出了费兹定律(Fitts’Law)，预测在人机交互中操作者控制一个物体从某一位置移动至目标区域所需要的时间[7]。

基于此，本文提出了基于费兹定律的可变导纳控制方法，通过费兹定律预测操作者拖拽机械臂的操作时间，构建合适的变导纳控制模型，在机械臂的拖动过程中对导纳控制阻尼参数进行自动调整，以提高机器人控制过程中的拖动效果以及操作的安全性。

1 基于费兹定律的可变导纳控制原理

1.1 导纳控制基本原理

导纳理论来源于机械阻抗、速度和作用力之间的关系，是一种基于广义惯量、阻尼和刚度的等效网络思想[8]，因此，该控制方法想要做到的是控制机械臂在与外界交互时所表现出的动力学特性。导纳控制相当于给机器人加上了虚拟的弹簧和阻尼，这就使机器人在与环境交互时会产生一种类似于谦让的特性。

导纳控制的期望模型在理论上有许多种表达方式，为了直观地表现出质量、阻尼、弹簧的运动特性，通常将模型表达为二阶线性定常微分方程，一般表达方式如下

(1)

式中Md,Bd,Kd分别为期望惯性、期望阻尼、期望刚度，Fh为操作者施加在机器人末端的力，x为笛卡尔空间内机械臂末端执行器的位置，xr为期望位置。因为惯量Md在人机协作的过程中影响很小，常用的导纳模型对其忽略不计[9]。因此，上式简化为

BdV+KdX=Fh

(2)

式中V为机器人末端输出速度。由于应用场景为颌面部手术中操作者将机械臂大范围移动拖拽至手术区域内，主要考虑柔顺性以及运动效果，不涉及运动限制不需要恢复力，因此,将期望刚度Kd设置为零。由此可知，人机协同控制中导纳控制本质上是对速度进行控制，控制器模型如下

BdV=Fh

(3)

1.2 费兹定律基本原理

根据费兹定律，预测在人机交互中操作者控制一个物体从某一位置移动至目标区域所需要的时间主要由两个因素所决定:1)起始位置离目标区域的距离A；2)目标区域的大小W。该定律常用的具体形式如下式

MT=a+blog2(A/W+1)

(4)

式中MT为预测时间，log2(A/W+1)称为难度指数(index of difficult,ID)，代表在该运动过程中需要进行传递的信息量，单位为bit。a,b为经验参数，操作设备不同，则这2个参数也会不同，具体求解方法是设置不同的难度指数并进行多次实验，记录操作时间与难度指数，通过拟合求得。

1.3 基于费兹定律的可变导纳控制器

导纳控制是一种将交互力作为系统输入，将机器人的位置或者速度作为系统输出的控制方法。在实际使用中根据任务场合不同，机器人也有不同的控制需求:有时需要机器人高速移动到指定位置，有时需要机器人进行精准慢速的控制[10，11]；对于柔性拖动环节，机器人协助操作者完成拉钩的放置任务，引导进行更加稳定的运动使拉钩到达手术位置，在这过程中，人与机器人之间是一种协作关系，将机器人高精度特点与人的高决策能力结合起来，实现较高的控制输出效果。

医生拖动手术机器人的过程中，在初始位置进行自由拖动时环境复杂度较低，拖拽力逐渐增加，而在接近手术目标区域时为保证安全性与精准性，拖拽力会逐渐减小，操作者的目标是精准而缓慢地将机器人运动至手术区域内。因此，要构建合适的变导纳控制模型，使其可以根据当前任务调整虚拟阻尼完成对不同控制模式的调整:人机交互力快速增大时，设定一个较小的虚拟阻尼值，操作者只需提供一个很小的力，即可操控机器人完成快速、灵活的运动；人机交互力递减时，使虚拟阻尼处于一个较大的值，操作者可以控制机器人完成精准且慢速的动作。本文设计的机器人导纳控制系统框图如图1所示。

图1 控制系统结构框图

上文得到的人机协同控制中导纳控制器的输出速度主要由导纳控制参数Bd决定，设

Bd′=Bd+δB

(5)

式中Bd′为修改后的导纳控制参数，δB为引入的变导纳因子，Bd为原期望阻尼值。在操作者拖动初期，应设定较小的虚拟阻尼起始值；随操作时间增加，虚拟阻尼值递增；在拖动机器人接近终点时以及超过预测时间后，应保持在较高的虚拟阻尼值。并且为保证费兹定律经验参数不变，Bd′满足以下的条件

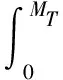
(6)

设定δB随时间线性变化，λ为线性变化率。Bd′满足:当t=MT/2时，Bd′=Bd；操作时间超过MT时，保持较大的导纳值。得到

(7)

将上式代入式(5)，得

(8)

2 实验设计与结果

2.1 实验设计

本文手术辅助机器人系统主要由六维力传感器、计算机、UR5机器人、拉钩等部分组成，主要任务为医生从初始位置P1拖动机器人至手术区域位置P2，拖动过程如图2所示。本文采用常州坤维KWR75系列六维力传感器，安装在机器人法兰与手术拉钩之间，由六维传感器检测手术拉钩受到的力信号。主要结构如图3所示。

图2 机器人拖动过程示意

图3 力传感器与手术拉钩

由式(4)可知，费兹定理在人机交互时的常用模型，公式中经验参数通过多次试验并拟合求得。为求得经验参数进行固定参数的机械臂点对点拖动实验,分别取不同的ID指数进行试验，操作者通过拖拽将拉钩移动至立方体区域内，如图4所示，其中，A为拉钩与立方体区域的距离，W为立方体区域的大小。实验中，分别设置如表1所示的5组不同的难度指数，由3名操作者多次拖动机械臂，取操作时间平均值进行线性拟合。拟合结果如图5。

图4 拖动测试示意

表1 不同ID的平均操作时间

图5 移动时间与难度指数拟合结果

为评价本文中提出的变导纳控制算法性能，利用MATLAB进行仿真验证。为方便表达演示,可以只考虑机器人末端执行器笛卡尔空间某一维的情况,它可以代表空间任意维，假设机器人初始速度为零，阻尼参数5(s·N)/m，线性变化率λ为0.25，输入力为正弦信号，设置3组不同的难度指数ID并进行仿真对比实验。

进一步，为讨论本文所提出的变导纳控制算法中线性变化率λ对控制效果的影响，设计2组对比实验分析，初始条件不变，设置2组不同线性变化率进行仿真对比实验。

2.2 实验结果

实验结果如图6所示，对比机器人的位置状态可以发现，在运动启动段时，利用本文所提出的变导纳参数控制相比于固定导纳参数控制响应更快，并随着难度指数ID增加，在运动初期的控制效果更加明显，在输入力不变的情况下，运动更加快速。

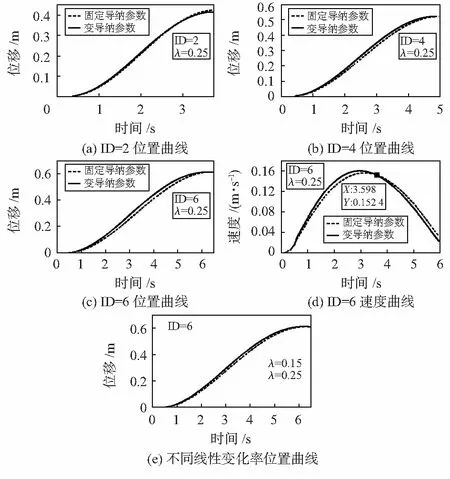
图6 固定导纳参数与变导纳配置参数的机器人响应对比实验结果

如图6(c),(d)分别为难度指数为6时的机器人仿真位置曲线与速度曲线，0～3.6 s前变导纳控制算法设置较低的导纳值，机器人运动速度更快；在运动后期导纳值递增，机器人运动速度快速下降，在运动后期机械臂末端接近目标区域时阻尼参数增大，位置曲线相较固定导纳参数控制方法更加平缓，满足运动末期的精准性和平稳性要求。为讨论线性变化率λ对控制效果的影响，选择难度指数为6，改变线性变化率观察实验结果，如图6(e)所示，线性变化率增大可以提高运动速度，总体运动控制效果差异度较小，因此，根据实际情况选取合适的线性变化率即可。

3 结 论

本文根据手术机器人在辅助颅颌面部手术过程的任务中对于人机协同交互的实际需求，提出了一种基于费兹定律的变导纳控制方法，该方法应用于医生将机器人从起始位置拖动至目标位置的快速移动，结合费兹定律对操作时间进行预测，在拖动的过程中实时改变导纳系数以满足不同运动阶段的控制需求。

仿真实验结果表明：基于费兹定律的变导纳控制方法与固定导纳参数控制方法对比,提升了不同阶段的控制效果，使机器人在运动初始位置较快移动、在接近目标区域时进行精准慢速的运动，也可以满足手术机器人移动过程柔顺性的要求。