棱锥图若干性质的研究
侯胜哲
(吉林化工学院, 吉林 吉林 132022)
图G1与图G2的联图是指图G1的每个顶点G2和的每个顶点相连的图,记作G1∨G2.锥图(cone graph)指的是圈Cm与空图On的联图Cm∨On,记作Pm,n(如图1).图G中经过每个顶点的圈称为图G的哈密顿圈;一个包含哈密顿圈的图称为哈密顿图.图G的邻接矩阵A(G)的特征值及其重数叫做图G的邻接谱.使得图G中相邻两点着不同颜色所需要的最少颜色数,称为图G的色数.
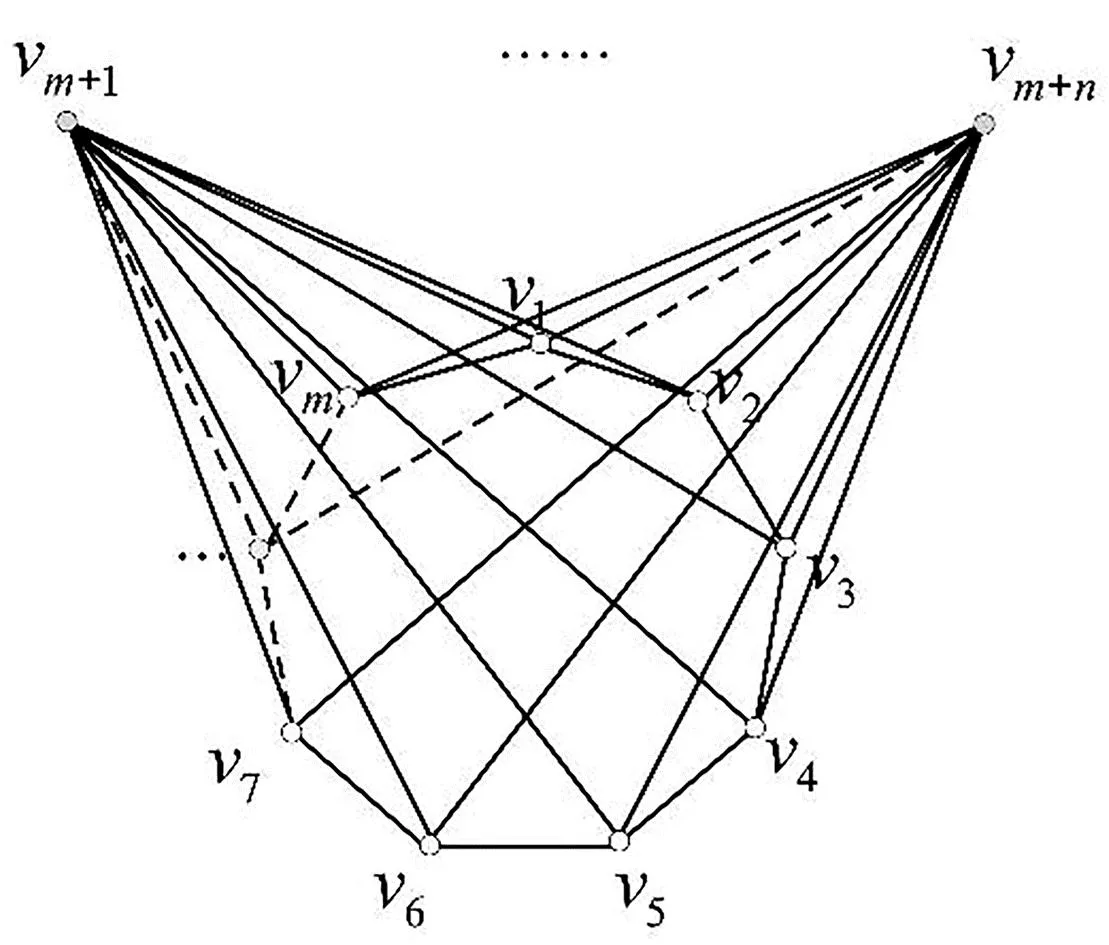
图1 锥图Pm,n
锥图最早是Buckley和Harary[1]在研究广义轮图时提出的,但未正式命名,也未深入探究.Gallian[2]等人在研究优美图时,发表了数篇文章对锥图进行了简要说明.最近几年,Daouda[3]研究了锥图的生成树的个数;Bosco等[4]给出了锥图的无线电平均D-距离数(radio mean D-distance number);徐连诚等[5]给出了锥图的独立数的确切值. Pan等[6]研究了锥图的多重着色问题.Kook[7]研究了特殊锥图的α-不变性.Alfaro等[8]研究了以任意图为基图所构造的锥图的沙堆群;吴宝丰等[9]研究了基于正则图的锥图的Q-谱确定性;郑文萍在她的博士论文中[10]研究了锥图等一系列图的交叉数问题.
本文主要研究了多锥图的色数、可平面性、邻接矩阵、邻接矩阵特征值(谱)、哈密顿性.
1 棱锥图的色数与可平面性
轮图(wheel graph)Wn(如图2)的定义为圈Cm与一个点的联图,即Cm∨O1,易知Pm,1(如图3)即为轮图Wm;Pm,2为双锥图(如图4,5,6).
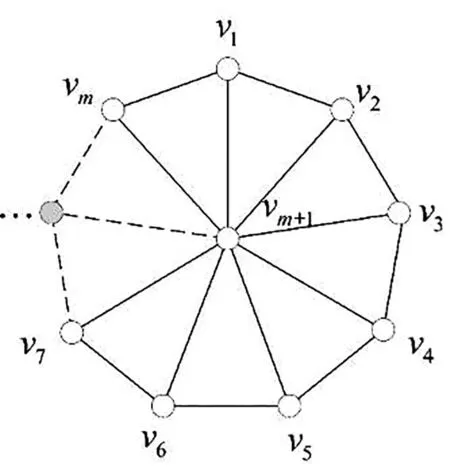
图2 轮图Wm
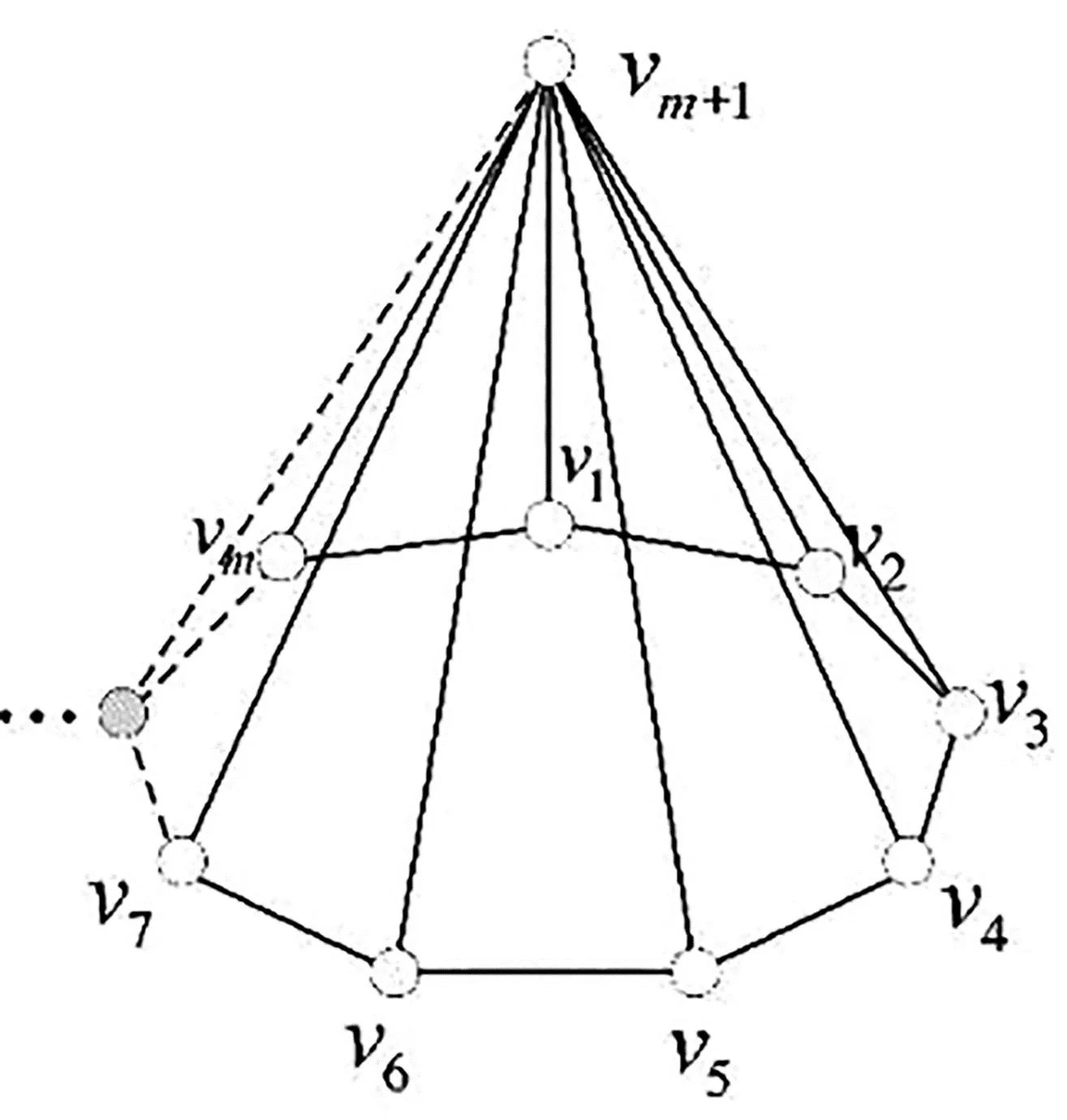
图3 棱锥Pm,1
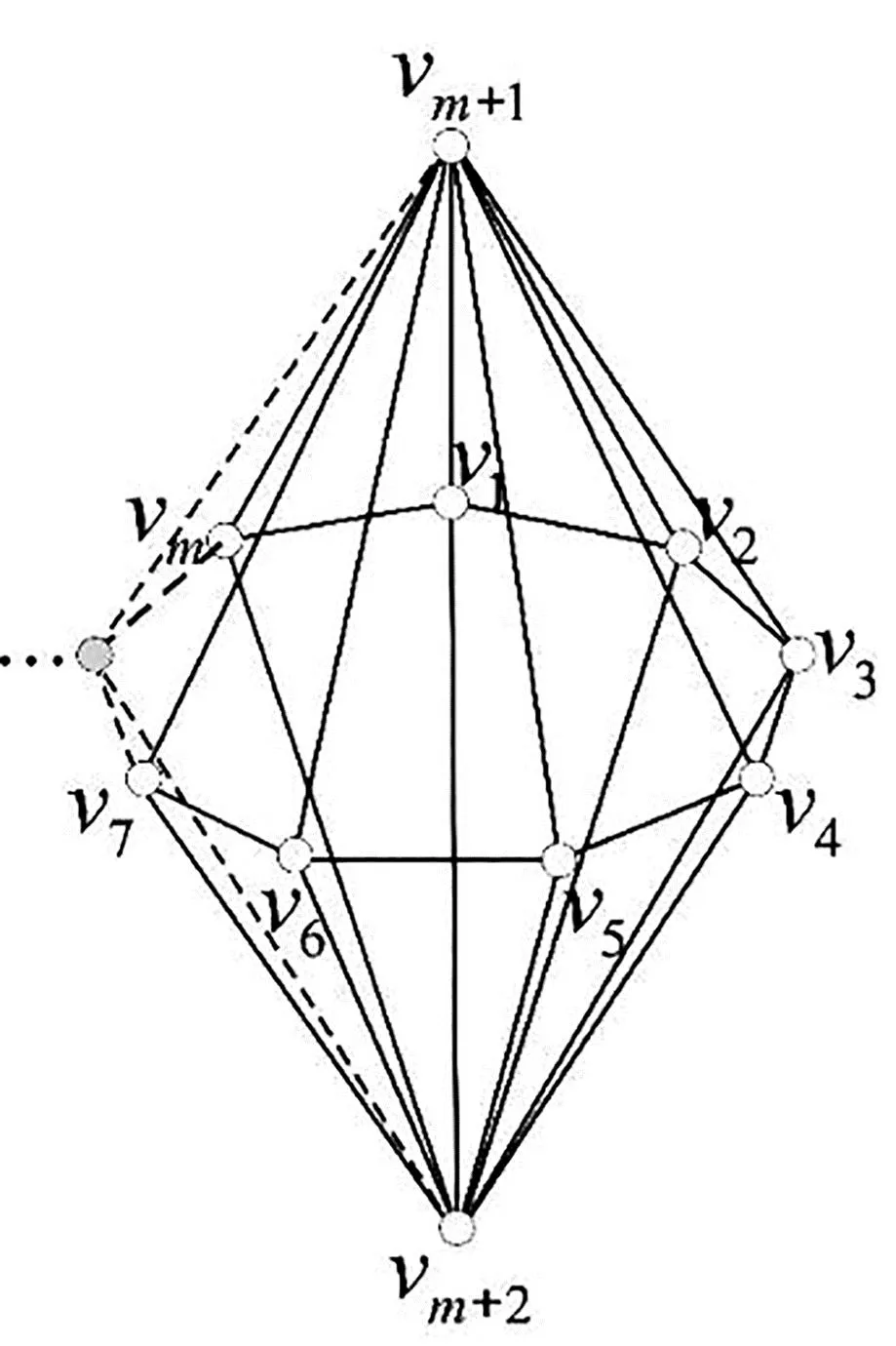
图4 双锥图Pm,2
定理1.1P3,1为完全图K4,P4,2为完全3部图K2,2,2,P4,n为完全3部图K2,2,n.
证明事实上,P3,1为四面体(tetrahedral)骨架图所对应的平面图;P4,2为八面体(octahedral)骨架图对应的平面图,即K2,2,2(如图5);P4,n为完全3部图K2,2,n(如图7).

图5 P4,2为K2,2,2
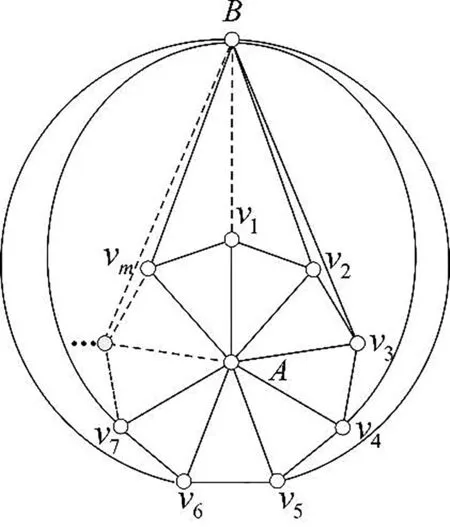
图6 棱锥图Pm,2是平面
定理1.2当锥图的顶点划分尽可能少时,Pm,n可为4部图.
证明在锥图Pm,n=Cm∨On中,若Cm是偶圈时,Cm的顶点集可以用两种颜色正常着色,空图On中的点用第三种颜色,此时Pm,n为完全3部图;若Cm是奇圈时,Cm的顶点集需要用三种颜色才能正常着色,而空图On中的点和Cm中的每个点相邻,故On中的点必须取另一种颜色.此时Pm,n需要4种颜色才能正常着色,把每种颜色看作一个划分.故Pm,n是4部图.
推论1.3锥图Pm,n是四可着色的.
定理1.4锥图Pm,n在n=1,2时是平面图;锥图Pm,n(m≤3,n≥3)是平面图;锥图Pm,n(m≥3,n≥3)不是平面图.
证明(1)Pm,1与轮图同构显然是平面图,如图6所示;对于Pm,2,O2中的点设为A和B,将A点与Cm的顶点的连边按轮图的平面图Wm画出,将B点放置在最外侧的无界面,再分别连接Cm上的点,该种连接方式可以做到与Wm边不交,这显然是Pm,2的一个平面嵌入.
(2)对于P1,n,n≥3根据定义P1,n=C1∨On, 即为星图K1,n, 显然是平面图.对于P2,n, 根据定义P2,n=C2∨On, 容易得到P2,n的一个平面嵌入(图8), 易知P2,n是可平面的.
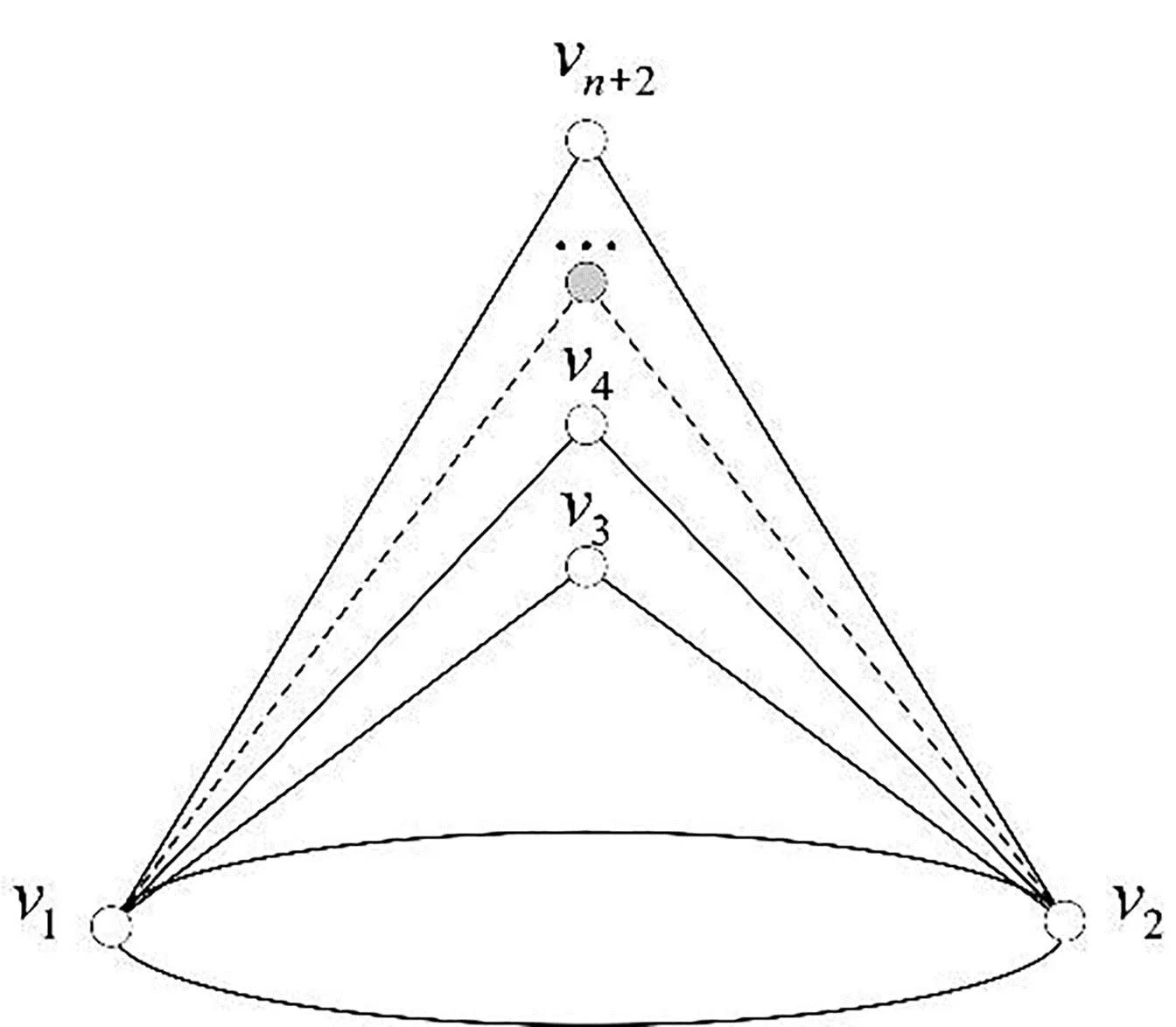
图8 锥图P2,n是平面
(3)对于P3,3, 我们有P3,3-E(C3)≅K3,3(图9和图10),P3,3包含一个K3,3的子图,根据Kuratowski定理,故其是非平面图.当Pm,n(m≥3,n≥3),任取Cm中的三个点和On中的三个点, 在这六个点中间只保留Cm与On之间的边,故形成了K3,3,所以Pm,n都包含了K3,3,知其都是非平面图.

图9 P3,3含有K3,3

图10 K3,3
众所周知,四色定理保证“每个平面图都是四可着色的”,那么自然会问“每个四可着色的图都是平面图”对吗?由推论1.2和定理1.3可知,答案是否定的,锥图Pm,n就是一个反例.
2 锥图的邻接矩阵(谱)与哈密顿性
在本节中的圈Cm都满足m≥3.在下面的定理3.3中分别用Pm,n来表示锥图Pm,n的邻接矩阵,Cm表示圈Cm的邻接矩阵,On表示空图On的邻接矩阵,Em代表m阶的单位阵.
对于锥图Pm,n=Cm∨Om,给定一种顶点标号方式记为(*):先将Cm按照顺时针方向进行标号v1,v2,…,vm,接着对其它n个独立顶点进行任意标号vm+1,vm+2,…,vm+n.

例2.1画图(如图11所示),并求出P4,6的邻接矩阵,并验证定理2.1.

图11 P4,6
解:如图12与定理2.1吻合.

图12 A(P4,6)
引理2.1[11]在一个有向简单图(对于无向图亦成立)的邻接矩阵中,若能找到一组n个1,使得其中任意两个1不在同一行也不在同一列,且不关于主对角线对称,则该图为哈密尔顿图.
定理2.2锥图Pm,n(m≥n)是哈密顿图.
证明当m≥n时,在右上角的分块矩阵In,m、左下角的分块矩阵Im,n中显然可以找到n个既不同行也不同列的1,根据引理2.1可知,锥图Pm,n(m≥n)是哈密顿图.
注: (1)定理2.2也可以利用定义法证明,按照(*)的标号方式,顶点v的角标按照1-(m+i1)-2-(m+i2)-…-(m+in)-n-(n+1)-(n+2)-…-m,其中i1,i2,…,im∈[1,n]∩N+,进行标号,便得到至少一个哈密顿圈,故其为哈密顿图.
(2)m的值要大于等于n,例如P4,6就不行,但是P4,3可以,1-(m+i1)-2-(m+i2)-3-(m+i3)-4-1,其中i1i2,…,i3∈[1,3]∩N+.
当然Pm,n不一定是欧拉图很好判断,因为每个点的度不一定是偶的.
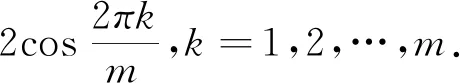
证明
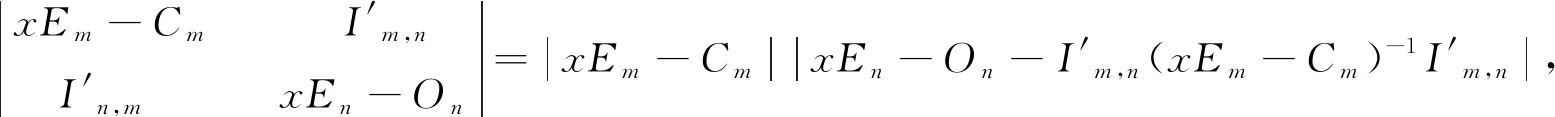
例2.2利用P6,7、C6和P7,5、C7验证定理2.3的结论.
解:(1)P6,7的特征多项式为f(A,P6,7)=(x-1)2x6(x+1)2(x+2)(x2-2x-42),C6的特征多项式为f(A,C6)=(x-2)(x-1)2(x+1)2(x+2), 可以看出除了2这个根以外,P6,7的特征根中必含有C6的特征根.
(2)P7,5的特征多项式为f(A,P7,5)=(x-7)x4(x+5)(x3+x2-2x-1)2,C7的特征多项式为f(A,C7)=(x-2)(x3+x2-2x-1)2, 可以看出除了2这个根以外,P7,5的特征根中必含有C7的特征根.

证明


