费米耀变体和射电噪类窄线赛弗特1 星系之间的关系

黄 霞，陈永云，马 力，李怀珍

（1.昆明医科大学 海源学院，云南 昆明 651700；2.曲靖师范学院，云南 曲靖 655000；3.云南师范大学 物理与电子信息学院，云南 昆明 650500；4.玉溪师范学院 物理与电子工程学院，云南 玉溪 653100）

0 引 言

Blazars 是活动星系核（AGNs）中特殊的一个子类，它的喷流指向观测者[1,2].多普勒效应增强了耀变体的喷流发射，因此它们呈现出很强的聚束效应.根据光学发射线的等值宽度（EW），Blazars 分为平谱射电类星体（FSRQs）和蝎虎天体（BL Lacs）.FSRQs 具有较强的发射线（EW ＞5A），BL Lacs的发射线则很弱甚至没有发射线（EW ＜5A）.然而，Ghisellini 等人认为用发射线等值宽度划分FSRQs和BL Lacs 并不是最好的指标，因此他们提出了FSRQs 和BL Lacs 之间更多的物理区别，他们发现FSRQs 和BL Lacs 可以用LBLR/LEDD～5×10-4来划分[3]，也有一些作者会用吸积盘光度在爱丁顿单位（LDisk/LEDD～10-2）来划分FSRQs 和BL Lacs[4,5]，FSRQs 的LDisk/LEDD＞10-2，而BL Lacs 的LDisk/LEDD＜10-2.他们认为，是由于吸积模式的变化而造成FSRQs 和BL Lacs 不同.

Osterbrock，Pogge 在1985 年发现了一类有趣的AGN 星系——窄线赛弗特1 星系（NLS1s）[5]，窄线赛弗特1 星系是赛弗特1 星系中的一个子类，它的特点是半峰全宽（FWHM）Hβ≤2 000 km/s，发射线较弱（OIII/Hβ＜3），有强的Fe II 发射线[6]，在软X 射线光谱波段有较明显的起伏、大振幅和快速的X 射线变化[7,8]，较小的黑洞质量（106～108）和较高的爱丁顿极限[9].NLS1s 通常认为是射电静类星系（射电噪度RL=Sradio/Soptical＜10，其中Sradio是5 GHz 辐射流密度，Soptical是在4 400 A 光学辐射流密度[10]）.因此，首次发现射电噪类窄线Seyfert 1 星系（RLNLS1s）RL ＞10 似乎很反常，只有5%～7%的NLS1s 是射电噪类的[11].因为RLNLS1s 具有致密的射电核、非常高的亮温度、高偏振的射电辐射流量和高的吸积率[12,13].因此，一些研究者认为blazars 和RLNLS1s 之间可能存在关系.Yuan 等人发现强RLNLS1s （RL ＞100）的光谱能量分布与blazars 相似[14]，Foschini 等人提出RLNLS1s 的中心引擎与blazars 的非常相似[15].Berton 等人认为RLNLS1s 可能是早期的低光度blazars[13].从而，可能存在RLNLS1 →FSRQs → BL Lacs 的演化系列[16].Singh、Chand 发现RLNLS1 经常会表现出与blazars 一样的特性，例如致密的射电核区、射电偏振等[17].Chen 等人发现RLNLS1 属于blazars 系列[18].

自从费米空间望远镜（Fermi-LAT）发射以来[19]，Fermi-LAT 陆续检测到一些NLS1s.这些具有γ射线发射的NLS1s 引起了天文学家的注意.特别是，γ射线的发射证实了NLS1s 中存在强的相对论喷流.更重要的是，这些γ射线通常是在RLNLS1 中被探测到.Sun 等人比较了GeV 波段的NLS1s 和blazars 的性质，他们发现GeV 波段NLS1s 的喷流特性更类似于FSRQs[20].Paliya 等人认为γ波段NLS1s 的观测性质与blazars 相类似[21].Paliya 等人发现γ波段NLS1s 的宽波带光谱能量分布（SED）类似于费米blazars，尤其是与FSRQs 相似[22].虽然耀变体与NLS1s 之间的关系已经有了一些研究，但是目前仍存在一些问题，如FSRQs、BL Lacs 和RLNLS1 之间的关系是什么？这三种不同类型的AGN 的喷流形成机制相同吗？是什么原因导致这三种星系的黑洞质量、吸积率或聚束效应之间的差异？

为了研究上述问题，我们采用Fermi blazars 和RLNLS1s 的大样本，通过喷流功率、黑洞质量、吸积盘光度、吸积率和核主导参数来探讨它们之间的关系.本文的第1 部分是样本，第2 部分是结果，第3 部分是讨论，第4 节是结论.本文采用以下宇宙学参数：H0=70 kms-1Mpc-1，Ωm=0.3，ΩA=0.7.

1 数 据

1.1 费米耀变体数据

本文中选取了费米耀变体的大样本，它们具有确定的红移、黑洞质量、宽线区光度、光学B 波段数据、光学V 波段数据、1.4 GHz 射电延展光度和1.4 GHz 射电核光度.我们采用Chen 等人的样本，他们已经收集了大量具有可靠红移、光学V 波段数据、1.4 GHz 射电延展光度和1.4 GHz 射电核光度的费米blazars 样本[23].我们从NED 得到了这些费米blazars 的光学B 波段数据，其中黑洞质量和宽线区光度来自Chen 和Xiong 等人，他们已经详细地描述了计算黑洞质量和宽线区光度的方法[24,25].

1.2 射电噪窄线赛弗特1 星系

我们还收集了具有可靠的红移、黑洞质量、宽线区光度、光学B 波段幅值、光学V 波段幅值、1.4GHz延展射电光度和1.4 GHz 射电核光度的rlnls1 的大样本.我们选用了Foschini 等人的样本，他们列出了42 个具有可靠的红移、黑洞质量、吸积盘光度和15 GHz 射电核流量的rlnls1[15]，并且从NED 中得到了这42 个RLNLS1 光学B 波段和 V 波段的数据.我们通过假设αcore=0，用15 GHz 射电核流量外推得到1.4GHz 射电核流量Score，从而得到1.4 GHz 延展射电光度，Sext=Stotal-Score，其中，1.4 GHz 的总射电流量Stotal来自NED.我们将RLNLS1 通过射电噪度参数（1.4 GHz 与光学B 波段流量之比，R1.4=F1.4GHz/FB-band）[10]分为低射电噪窄线赛弗特1 星系（L-RLNLS1s）和高射电噪窄线赛弗特1 星系（V-RLNLS1s）.当R1.4＜300 时，定义为L-RLNLS1s，当R1.4＞300 时，则定义为V-RLNLS1s.

Cavagnolo 等人使用了Chanard X 射线和射电数据研究喷流动能与射电光度的关系，他们发现喷流动能和延展射电光度之间有显著的相关性[26].为了避免聚束效应，Meyer 等人使用300 MHz 的低频射电延展光度来估计喷流的动能功率[27].因此，喷流动能功率不受聚束效应的影响，喷流动能功率计算公式如下.

喷流动能功率的单位是erg s-1.Zhang 等人将辐射能流密度从1.4 GHz 外推到300 MHz，并估算了AGN 的喷流功率[28].根据Meyer 和Zhang 等人文中提到的假设光谱指数α=1.2[27,28]，我们也将延展辐射能流密度从1.4 GHz 外推至300 MHz.并利用公式（1）得到喷流功率.

2 结 果

2.1 射电延展光度与红移和核心光度的关系

根据统一模型，FSRQ 和FRII 射电星系是统一的，而BL Lacs 和FRI 射电星系也是统一的，F-RLNLS1s的特性与FSRQ 类似.因此，我们在下文中讨论FSRQ、BL Lacs、RLNLS、FRII 和FRI 射电星系之间是否存在统一或演化关系.图1 左图显示的是1.4 GHz 延展射电光度与红移之间的关系，右图显示的是1.4GHz 延展射电光度与1.4 GHz 射电核光度之间的关系，实线表示FRI 和FRII 的界线[29].左图中，我们发现V-RLNLS1 和FSRQ 大部分在FRII 射电光度范围内，部分BL Lacs 则趋近FRI/FRII 的范围.结果表明，在V-RLNLS1、FSRQs 和FRII 射电星系之间可能存在一种统一的关系.同时，我们发现L-RLNLS1s的红移比费米blazars 小（见左图），这一结果可能表明这些L-RLNLS1s 是处于演化早期的类星体.

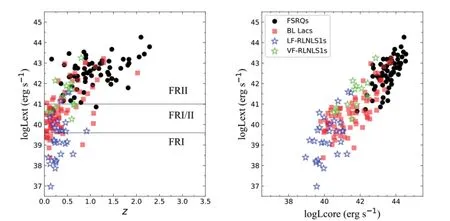
图1 1.4GHz扩展射电光度与红移之间的关系（左），1.4GHz扩展射电光度与1.4GHz射电核心光度之间的关系（右）.

从图1 的右图中，我们排除红移的影响（rx,y,z=0.74），通过偏相关回归分析后，得到射电核光度与射电延展光度之间存在较强的相关性.这种相关性意味着射电瓣的喷流与AGNs 的中心核区密切相关.我们还得到FSRQs 的logLcore平均值为，BL Lacs 的logLcore平均值为L-RLNLS1s的logLcore平均值为，V-RLNLS1s的logLcore平均值为我们发现V-RLNLS1s 比BL Lacs 具有更高的射电核光度，这一结果表明V-RLNLS1s 比BL Lacs 具有更强的聚束效应.

2.2 指向效应

强统一模型认为，观测AGN 的差异是由于多普勒效应（聚束效应）.我们用两个参数来描述聚束效应，即logRcore和logRv.采用射电核流量密度（Score）与延展射电流量密度（Sext）之比作为核主导参数（Rcore），它也被用作多普勒效应的指针[30].对流量密度进行k修正，最后用公式计算出核主导系数，其中αcore=0，αext=0.8.Kharb 等人使用另一个参数Rv作为MOJAVE blazars 样本的聚束效应指针[31].Rv是用射电核光度与经过k 校正的绝对V 波段星等（Mabs）的比值来定义[32]，即其中k修正光谱指数为αopt=0.5.根据Kharb 等[31]的方法，我们估算了费米blazars 和F-RLNLS1s 样本的Rv参数.

图2 是样本的logRcore和logRv分布图.从左图中，可以看到FSRQ 的logRcore在 0 到 2.5 的范围之内，其平均值为；BL Lacs 的logRcore分布范围从-0.5 到3.0，其平均值为；L-RLNLS1s 的logRcore分布范围从-1.0 到3.0，其平均值为；V-RLNLS1s 的logRcore分布范围从-1.0 到1.5，其平均值为通过K-S 检验，结果显示FSRQs 与V-RLNLS1s 的logRcore分布上存在显著差异，但在右图中两者之间没有显著差异.这个结果表明，FSRQs 与V-RLNLS1s 之间的差异可能是由于观测角度的不同造成的.

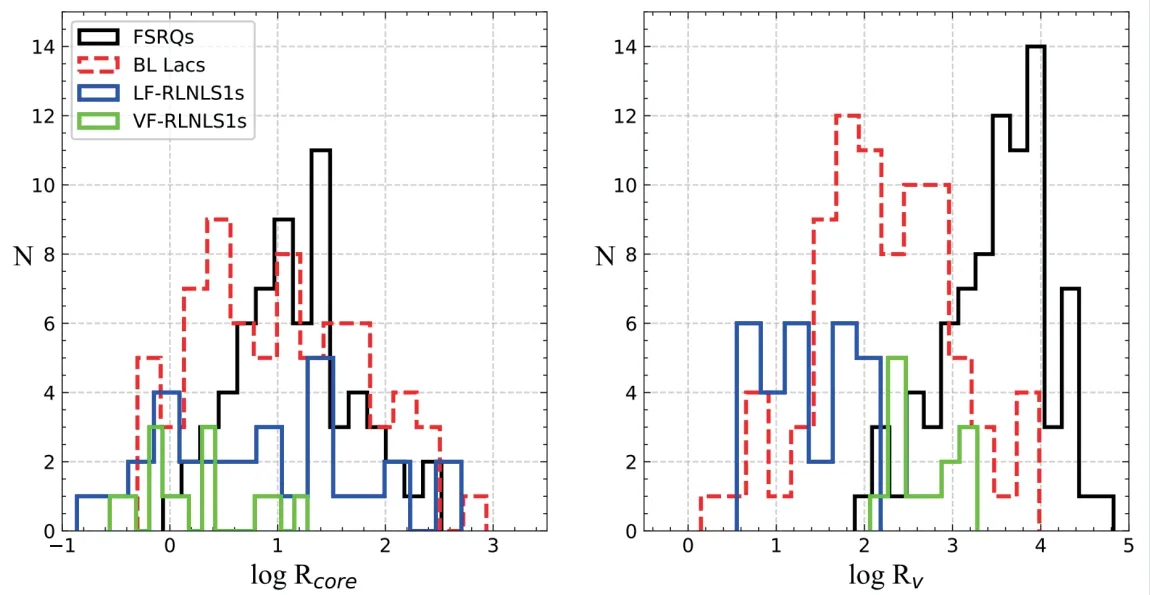
图2 logRcore（左）和 logRv（右）分布图.

从右图中，可以看出，FSRQs 和BL Lacs 的logRv具有明显的双峰分布，FSRQs 的logRv高于BL Lacs.FSRQs 的logRv分布范围在2.0 到5.0 之间，平均值为；BL Lacs 的logRv分布范围在0 到4.0 之间，平均值为；L-RLNLS1s 的logRv分布范围在0.5 到2.0之间，平均值为；V-RLNLS1s 的logRv分布范围在2.0 到3.3 之间，平均值为结果显示V-RLNLS1s 具有较高的logRv，这表明除了FSRQs，V-RLNLS1s 也具有较强的聚束效应.更重要的是，我们可以看到V-RLNLS1s 占据了FSRQs 分布的低logRv端.使用K-S 检验，我们发现不同类型间存在显著差异.这些结果表明，聚束效应可能导致不同AGNs 观测的差异.

为了比较Rcore和Rv，哪一个更好指示聚束效应，我们分别研究了它们与1.4 GHz 射电光度之间的关系.图3 的左图是logRcore与1.4 GHz 射电核光度的关系，右图是logRv与1.4 GHz 射电核光度的关系.我们发现，logRv与1.4 GHz 射电核光度之间存在强相关性，这一结果表明Rv比Rcore能更好的指示聚束效应.Kharb 等人在2010 年也发现了Rv能更好的指示聚束效应[34].Chen 等人研究了3 期费米blazars的Rv、Rcore和γ射线光度之间的关系，他们发现Rv和γ射线光度之间存在显著的相关性，他们的结果同样表明了Rv确实比Rcore能更好的指示聚束效应[23].图4 是1.4 GHz 射电延展光度与logRcore和logRv的关系图，从图中，我们还发现Rv似乎与延展射电光度显示出正相关性，然而，偏相关回归分析表明当排除logLcore的影响时（rx,y,z= - 0.15，p=0.056），Rv和延展射电光度之间没有显著的相关性，这个结果表明延展射电光度没有聚束效应.

欧阳修致力于收集古金石拓本，积至千卷，又将其为拓本所作题跋汇集，编为《集古录》(亦称《集古录跋尾》)一书，其子欧阳棐又编次其目，成《集古录目》。从内容上讲，这两本书显然各有不同，一则近于文章评论与史学考证，一则为专门目录；但从文献形态而言，二者皆以书籍的面目出现并传世。对朱熹来说，这些“古金石”的吸引力不仅来自其作为古物的一面，更是来自其作为文本或文献的一面，他更看重的是其“古金石文字”的属性。他将欧、赵二书进行比较，指出《金石录》“铨序益条理，考证益精博”，也着眼于其书籍与文献的属性，而无关于古物的收藏。从这一段话中也可以看出，在朱子看来，金石学与书籍及文献都有密切的关系。

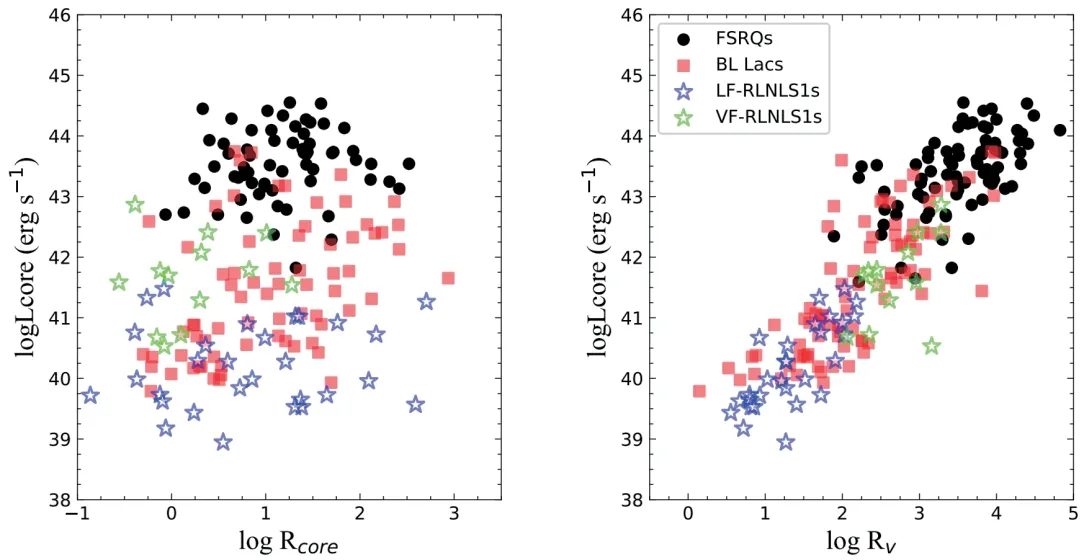
图3 1.4 GHz 射电核光度与logRcore 和logRv 的关系.

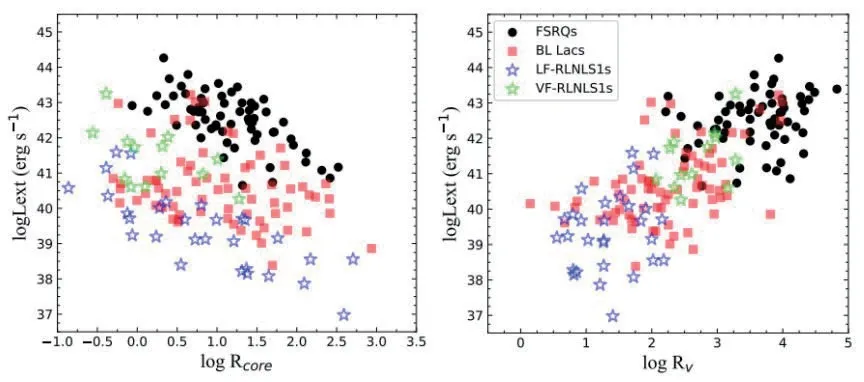
图4 1.4 GHz 射电延展光度与logRcore 和logRv 的关系.

2.3 喷流的性质

2.3.1 喷流功率的分布

图5 显示了喷流动能功率的分布.FSRQs 和BL Lacs 的喷流动能功率呈现双峰分布.FSRQs 的峰值为1045.5；BL Lacs 的峰值为1044.0.BL Lacs 和V-RLNLS1s 的喷流动能功率相同，L-RLNLS1s 的喷流动能功率最小（表1）.

表1 样本的平均值

图5 喷流功率的直方图.

2.3.2 喷流功率与爱丁顿比和喷流产生效率的分布

图6 左图显示了样本的喷流功率与爱丁顿比喷流功率之比（logPjet/LEdd）的分布.我们发现FSRQs和BL Lacs 的爱丁顿比喷流功率呈双峰分布；FSRQs 的平均值大于-2，BL Lacs 的平均值小于-2，同时，我们还发现，V-RLNLS1s 和FSRQs、BL Lacs 和L-RLNLS1s 的爱丁顿比喷流功率的分布大致重叠，经K-S检验得到，V-RLNLS1s 和FSRQs、BL Lacs 和L-RLNLS1s 具有相似的分布.

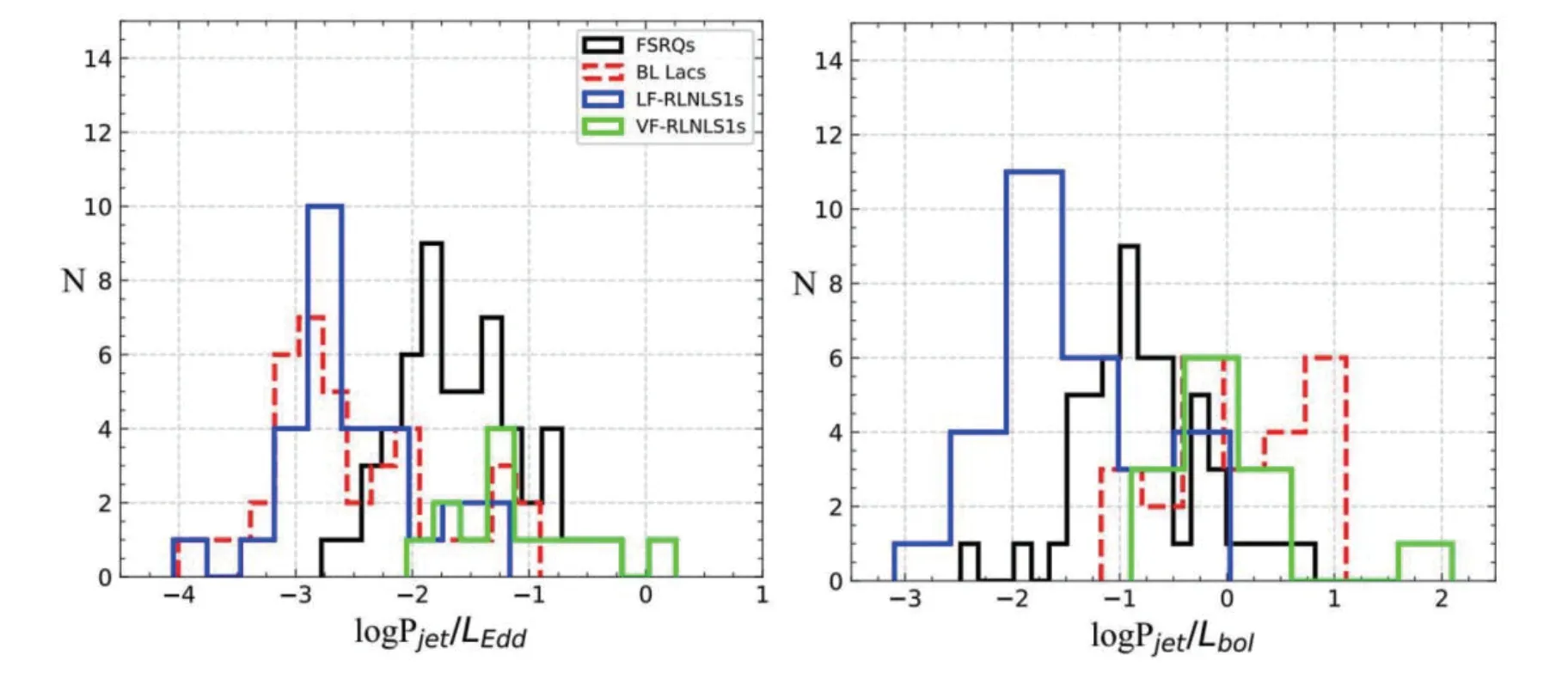
图6 爱丁顿比喷流功率(左)和喷流产生效率(右)的直方图.

2.3.3 喷流功率和黑洞质量

射电星系根据射电光度[36]分为两种类型，FRI 和FRII.Ledlow，Owen 利用180 个射电星系来研究FRI/FRII 分界，在1.4 GHz 射电光度与绝对星等的比中这种分界更加显著[29,37].Wu，Cao 使用logPjetlogMBH划分FRI 和FRII 射电星系[38].Xu 等人通过使用不同宇宙学参数对喷流功率和黑洞质量进行了修正[39]，可以表示为：

Blundell、Rawlings 认为因子f最有可能在10～20的范围内[40].图7 是FSRQs、BL Lacs、L-RLNLS1s和V-RLNLS1s 的黑洞质量（MBH）与射流功率（Pjet）之间的关系.值得注意的是，在logM-logPjet关系中，FRI 和FRII 使用f=10 和20 的分界线将FSRQs 和V-RLNLS1s 与BL Lacs 大致分离开，这支持了FSRQs、V-RLNLS1s 和FRII 是统一的射电星系.Willott 等人认为，f=10 可能是磁场演化的结果，他们发现f= 20对应于Lion/～2.5×10-2[41].

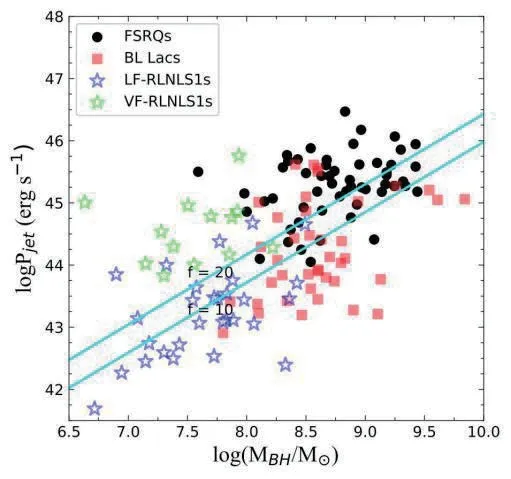
图7 黑洞质量与喷流功率的关系图.

2.3.4 喷流功率和吸积盘光度

图8 是喷流功率和吸积盘光度之间的关系，我们使用线性回归方法拟合喷流功率和吸积盘光度之间的关系（紫红色实线）.我们发现喷流功率与吸积盘光度有很强的相关性（r=0.64，p=3×10-15），关系式为：

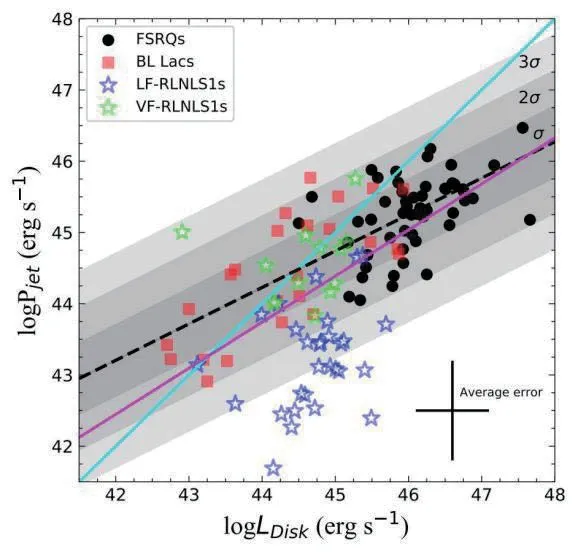
图8 喷流功率与吸积盘光度的关系.

我们还拟合了费米blazars 的喷流功率与吸积盘光度的关系（黑色虚线），关系式为：

同时还拟合了费米blazars 和VF-RLNLS1s 的射流功率与吸积盘光度的关系，关系式为：

青色实线表示喷流功率和吸积盘光度相等（Pjet=Ldisk），阴影区域对应1σ，2σ和3σ误差范围，其中σ= 0.5.平均误差棒对应logLDisk的不确定度为0.5，logPjet的不确定度为0.7.喷流功率与吸积盘光度有显著的相关性，表明喷流与吸积关系密切.有趣的是，当包含V-RLNLS1s 样本时，费米blazars 的斜率没有显著变化，说明V-RLNLS1s 遵循费米blazars 的logPjet-logLDisk关系.但是，L-RLNLS1s 不遵循这种关系，这些结果更可能说明V-RLNLS1s 喷流的形成机制与费米blazars 相似.我们还发现大多数FSRQs、L-RLNLS1s 和V-RLNLS1s 具有logPjet＜logLDisk，这可能意味着这些源具有强的吸积盘.

3 讨 论

3.1 射电噪类窄线赛弗特1 星系的喷流功率

一般认为喷流功率与黑洞质量之间有一定的关系.大的黑洞质量可能导致高喷流功率.一些作者认为，当喷流功率被黑洞质量归一化时，黑洞系统具有类似的喷流功率[15,22].我们用喷流功率除以爱丁顿光度，发现V-RLNLS1s 和FSRQs、L-RLNLS1s和BL-Lacs 的logPjet/LEdd有相似分布（表2）.Heinz，Sunyaev 提出，喷流功率与黑洞质量成比例，即Pjet∝（归一化的喷流功率），这适用于高辐射效率和低吸积率[42].我们研究了整个样本的Pjet∝的分布情况（图9）.我们发现，L-RLNLS1s 和V-RLNLS1s倾向于具有高归一化的喷流功率.这些结果意味着，L-RLNLS1s 和V-RLNLS1s 由于低的黑洞质量导致低的喷流功率.

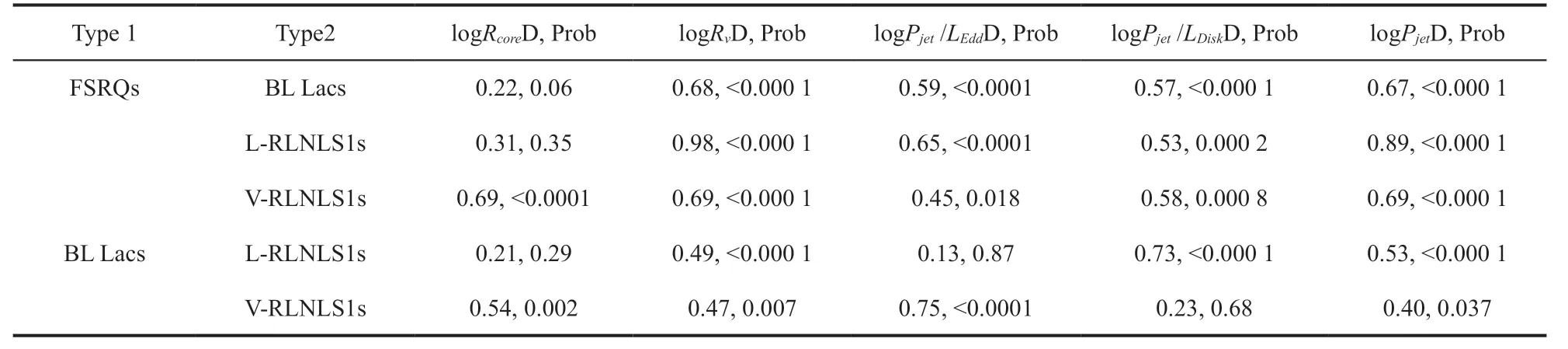
表2 样本的K-S 检验

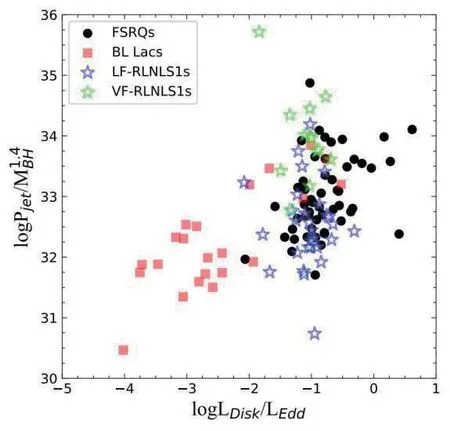
图9 喷流功率和吸积率的关系.

3.2 费米blazars、RLNLS1s 和射电星系的统一

通常认为blazars 和射电星系具有相同的物理特性.他们的观测差异是由于多普勒聚束效应引起的各向异性辐射[1].Hovatta 等人比较了FSRQs、BL Lacs 和射电星系的多普勒因子分布，他们发现FSRQs和BL Lacs 的多普勒因子高于射电星系[43]，这表明blazars 具有较强的聚束效应，而射电星系的聚束效应较弱.许多研究者已经通过使用相对较小的样本证实了blazars 和射电星系之间的统一情况[24,39]，在本文中，我们发现基于1.4 GHz 延展射电光度和红移的关系，FSRQs 位于FRII 区域（图1）中.此外，我们还发现FSRQs 和BL Lacs 被Ledlow、Owen[29]的FRI/FR II 分界线分开，这些结果支持了FR I/FR II 与BL Lacs/FSRQs 之间的统一性.

到目前为止，γ射线的NLS1 通常在RLNLS1 中被探测到，这说明RLNLS1 有强相对论喷流.为什么这些RLNLS1 有一个强的相对论喷流？Paliya 等人研究了γ射线的NLS1 的物理性质，他们发现，相较于blazars，γ射线的NLS1 具有更低的多普勒因子[22].根据Urry、Padovani[1]的统一模型，AGN 的观测差异可以通过使用视角的差异解释，即聚束效应.随后，Shen 和Ho 建议，可以使用两个简单的量：爱丁顿比（相对Fe II 强度RFeII）和指向效应（Hβ的FWHM）来解释不同类型的AGN[44].我们研究Fermi 类星体和RLNLS1s 的吸积率（LDisk/LEdd）和指向效应（logRv）.尽管L-RLNLS1s 和V-RLNLS1s的吸积率分布类似于FSRQs，但FSRQs 倾向于具有较高的logRv.使用K-S 测试，L-RLNLS1s、V-RLNLS1s和FSRQs 在logRv的分布上存在显著差异（表1）.我们的结果证实，可以使用吸积率（LDisk/LEdd）和指向效应（logRv）来解释AGN 之间的观测差异.

Ledlow 和Owen 发现可以用射电喷流功率和寄主星系绝对星等之间的关系来将FR I/FR II 分类[29].我们研究了费米blazars 和RLNLS1 的射电功率与黑洞质量之间的关系.通过使用FR I/FR II 分界线（图7），把FSRQs 和V-RLNLS1 大致与BL Lacs 分隔开.FSRQs 和 V-RLNLS1 位于 FR I/FR II 分界线之上，而BL Lacs 和 L-RLNLS1 位于该分界线之下.此外，基于1.4 GHz 延展射电光度和红移，FSRQs 和V-RLNLS1倾向于位于FR II 区域，而L-RLNLS1 倾向位于FR I 区域（图1）.这些结果暗示了FSRQs、V-RLNLS1和FRII 射电星系的统一.

3.3 喷流吸积关系

人们普遍认为，喷流与吸积之间存在着密切的联系.许多研究者已经证实喷流和吸积之间存在着密切的相关性[22,24,25].根据 Heinz、Sunyaev[42]的理论，喷流和吸积之间的关系也可以用来理解相对论喷流的统一[16].研究 RLNLS1 是否也遵循同样的模式是很有意义的.同时，比较低黑洞质量系统和高黑洞质量系统（即费米blazars）的喷流-吸积关系也很有趣.这个比较将使我们理解驱动这两种AGN 的中心引擎的异同.

我们发现整个样本的喷流功率与吸积盘光度之间有很强的相关性，这表明喷流与吸积有密切的联系.此外，V-RLNLS1 遵循费米blazars 之间的logPjet-logLDisk相关性.然而，L-RLNLS1 则不遵循，它们的喷流功率明显比费米blazars 小很多，而盘光度与低喷流功率的费米blazars 差不多.这些结果表明V-RLNLS1 的喷流形成机制与费米blazars 相似.

我们还发现大多数FSRQs、L-RLNLS1s 和V-RLNLS1 的logPjet＜logLDisk，而大多数的BL Lacs 的logPjet＞logLDisk.可能的解释是：FSRQs、L-RLNLS1s 和V-RLNLS1s 是年轻的AGN，它们具有低的黑洞质量，高的吸积率和辐射效率.随着时间推移，FSRQs, L-RLNLS1s 和V-RLNLS1s 将具有更低的吸积率和更低的吸积效率.当LDisk/LEdd＜- 2 时，吸积模式发生改变，具有较低的辐射效率，因此 L-RLNLS1s、V-RLNLS1s 和FSRQs 变成了BL Lacs[16].

4 结 论

我们使用了大样本的费米blazars 和F-RLNLS1s 研究它们之间的关系，得到了以下结论：

（1）与BL-Lacs 和L-RLNLS1s 相比，V-RLNLS1 具有较高的logRv，这一结果表明V-RLNLS1 具有很强的聚束效应.

（2）通过FRI 和FRII 之间的分界线（logPjet-logMBH），V-RLNLS1 和FSRQ 与BL Lacs 能被分开，这些结果表明FSRQ、V-RLNLS1 与FRII 射电星系统一.

（3）V-RLNLS1 遵循费米blazars 中的logPjet-logLdisk相关性，这些结果表明V-RLNLS1s 喷流的形成机制类似于费米耀变体.

（4）大多数L-RLNLS1、V-RLNLS1s 和FS RQ 具有logPjet＜logLdisk，这支持L-RLNLS1s、V-RLNS1和FSRQ 可能具有很强的吸积盘.