基于改进局部保持投影算法的轴承故障特征提取*

刘庆强，曹 栩

(东北石油大学电气信息工程学院，大庆 163318)

0 引言

由于现代工业技术飞速发展的推动，在工业领域中每天都将面临着海量的数据，这些数据具有多样、高维的特点，因此基于这些数据的分析与计算带来了一定的困难。为了解决这一难题，流形学习作为一种高效的数据处理方法被提出，其可以极大地提高数据的处理效率和性能。流形学习方法可分为全局和局部算法，等距映射(isometric feature mapping，ISOMAP)[1]是经典的全局算法，局部线性嵌入(locally linear embedding，LLE)[2]、拉普拉斯特征映射(laplacian eigenmap，LE)[3]、局部保持投影(local preserving projection，LPP)[4]、局部切空间排列(local tangent space alignment，LTSA)[5]等均为经典的局部算法。其中全局算法能够较好的保持数据的本质流形结构，但其存在时间复杂度高、不利于工业数据应用的确缺点；而局部算法通过挖掘数据的局部结构，保持样本点的局部结构在降维前后不变，从而降低了计算的复杂度，得到了广泛应用。

LPP作为经典的局部流形学习算法，其具有线性降维算法简单的优点，同时也有非线性问题处理的能力，因此LPP算法已广泛应用在人脸图像分析、模式识别、故障诊断等领域。但在原始的局部保持投影算法中，使用欧氏距离度量样本间的相似性再由K近邻算法得到局部邻域图，并不能有效地应用于高维非线性数据结构中。因此近年来许多学者对近邻点的度量方式提出了不同的改进方法，其中ISOLLE(LLE with geodesic distance)算法[6]使用测地线距离来度量近邻点，较好的保持了流形的全局结构；戴永奋等[7]提出以马氏距离为度量的局部保持投影算法；王海燕等[8]提出样本列信息与自适应邻域图的局部保持投影算法，根据不同样本所对应的同一维度信息统计加权从而度量样本间的相似性。甘航萍等[9]利用凸轮权重距离代替欧氏距离构造邻接图有效地处理了数据分布不均匀所造成的度量问题；李霁蒲等[10]提出一种近邻概率距离用于度量近邻点的相似性。以改进算法均采取不同的距离进行样本相似性度量，但均未考虑到非线性数据间存在的相关信息，影响样本相似性度量的准确性，从而破坏高维非线性数据局部结构的保持。

因此，本文提出了基于相关性Rank-order度量的局部保持投影算法。该方法首先采用相关系数计算数据间的相关性距离信息，并对相关性高的数据中使用Rank-order距离度量数据点之间共享的近邻信息从而提高相似性度量的准确性，其次再构造局部近图进而计算其权重，进行局部线性映射到低维空间。最后在公开标准的轴承故障数据集和实验室实际采集的轴承故障数据集上的实验表明，所提算法具有较好的特征提取效果。

1 局部保持投影算法

局部保持投影算法(LPP)的主要思想是通过构建近邻图在保持数据局部结构特征不变的条件下，将高维数据X通过投影矩阵P映射为低维数据Y，使得在高维空间中的近邻点在低维空间中也保持近邻。LPP算法通过优化以下目标函数求解投影矩阵P：

(1)

式中，wij为数据xi与xj投影权值。即：

由式推导，投影矩阵P由以下目标函数获得，即：

argmintr(PTXDXTP-PTXWXTP)=argmintr(PTXLXTP)

(2)

式中，D为对角矩阵，即D=∑ijWij；L=D-W为拉普拉斯特征映。

最后引入约束条件PTXTDXPT=1，则式(2)最优问题转化为求解广义特征值问题：

XLXTP=λXDXTP

(3)

则求出前m个最小特征值对应的特征向量构成的投影矩阵P，即P=[p1,p2,…,pm]。最后则由Y=PTX得到低维投影数据。

2 相关性Rank-order距离

在数据处理过程中，如果采用欧氏距离度量数据间的相似性，缺失了数据间相关性信息并不能很好地挖掘每个数据点在高维空间中局部流形结构，同时也忽略了数据间的相对位置关系从而不能选择出真正有效的近邻点[11]。其中Rank-order距离[12-13]利用数据点间共享的近邻点位置信息从而计算两个数据点间的距离。由此本文提出了相关性Rank-order距离，在Rank-order度量的基础上，通过加入数据相关距离信息不仅保持了高维数据点之间的流行结构，而且可以由效提高数据距离度量的可靠性。其相关示意如图1和图2所示，图1中黑灰两点仅依靠欧氏距离来度量两者的相似性，而图2中，将黑灰周围近邻点的相关性考虑在内，从而进行相似性度量。其中黑线表示与黑色点近邻，灰线表示与灰色点近邻。

图1 欧氏度量 图2 相关性Rank-order度量

其步骤可总结为：

步骤1：由式(4)和式(5)计算每个数据点与其它点之间的相关距离并按升序排列。

(4)

d(xy)=1-ρ(xy)

(5)

步骤2：根据各数据点之间的相关性，计算每两个数据点之间的非对称相关性Rank-order距离，计算公式为：

(6)

式中，fxi(m)为在xi的相关性近邻列表中第m个近邻数据点；Oxi(xj)为xj在xi相关性近邻点列表中的位置，即xj为xi的第几个近邻点。当xi与xj之间的非对称相关性Rank order距离越小，说明它们共享的近邻点相关性越高，近邻点间结构越相似。如图3所示。

图3 相关性Rank-order距离

步骤3：将D(xi,xj)距离对称化和归一化得到相关性Rank-order距离(CRD距离)，即：

(7)

3 改进的局部保持投影算法

局部保持投影算法常使用欧氏距离度量样本间的相似性，从而选择k个近邻构建邻域图，然而对于高维空间中大量复杂的非线性数据点，欧氏距离度量对近邻点的选择并不可靠，会破坏高维局部结构的保持[14-15]，影响算法的特征提取能力。因此，本文给出相关性Rank-order距离定义及步骤替换局部保持投影算法中的欧氏距离，其他步骤与局部保持投影算法步骤一致，其伪代码描述如下：

输入：原始数据集X={x1,x2,…,xn}∈RD，目标维数d≪D，初始邻域参数k。

输出：d维向量Y。

步骤1：运用相关系数公式计算每个样本点xi与其其他样本点间的相关距离，并对距离信息进行升序排列。

步骤2：计算相关性Rank-order距离。

fori=1 toN

end

步骤3：根据相关性Rank-order距离查找每个数据点的K近邻点并构建邻域图。

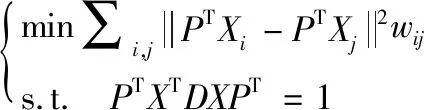
步骤5：由式Y=PTX计算得到d维数据Y。

4 实验

4.1 实验数据

实验所使用的CWRU数据集是由凯斯西储大学(CWRU)提供的公开轴承故障数据。其采集装置如图4所示，主要由电机、扭矩传感器、测力计及电子设备组成[17]。该数据集在电机转速为1797 rpm，轴承负载为0，采集频率为12 kHz条件下获得的，共包含4类数据，分别为：正常轴承数据、滚珠故障数据、轴承内圈损伤数据、轴承外圈损伤数据，其中损伤直径为0.007 in。每一种类型的数据共采集了100个样本点，每个样本的维数为1024。

图4 CWRU实验平台 图5 实验室测试平台

NED数据集为实验室测试平台上采集的轴承数据，其采集装置如图5所示，由电机、轴承和变速箱组成。通过由加速度计和模拟量采集模块采集振动信号。该平台配有3个不同位置有损伤的轴承：内圈、滚珠和外圈及无损伤的正常轴承。一共采集了4类数据，分别为：正常数据、滚珠故障数据、内圈损伤数据和外圈损伤数据。采集的数据负载为0 hp，采样频率为10 kHz。其中每一中类型的数据共100个样本，每个样本的维度为1024。

4.2 实验结果及分析

首先，为了验证本文所提改进算法在特征特征提取中的有效性，在第一组实验中将CWRU数据集经过预处理得到的时频域特征作为原始特征集，分别使用LLE算法、LE算法、LPP算法及本文改进算法CRO-LPP将提取的样本特征投影到三维空间中。图6为算法在CWRU数据集上的实验结果，其中近邻点个数为K=12，其他参数保持不变。由于有效的低维数据是进行分类识别最重要的特征，进而实现了重要特征提取。由图6可以看出，在欧氏距离的度量下，LLE、LTSA算法所提取的特征在低维空间中出现了不同程度的混叠可分性较差，无法有效识别样本类型。LPP算法和LE算法只能将其中两类故障特征有效地分离。而在CRO-LPP算法中所提取的特征在异类可分离性表现明显，同时也具有较好的聚类效果。

(a) LLE算法 (b) LE算法

图6中，红点为正常数据；绿点为内圈损伤数据；蓝点为滚珠故障；黑点为外圈损伤数据。

在第二组实验中将定量评估算法性能，引入了Fisher测度作为评估的指标[16]。该指标将通过类间散度与类内散度的比值，衡量样本之间的分离程度，其值越大，则说明该算法提取到样本特征的可分离性就越好。其定义为：

F=tr(Sb)/tr(Sw)

(8)

式中，Sb、Sw分别为样本的类间散度和类内散度，定义如下：

(9)

(10)

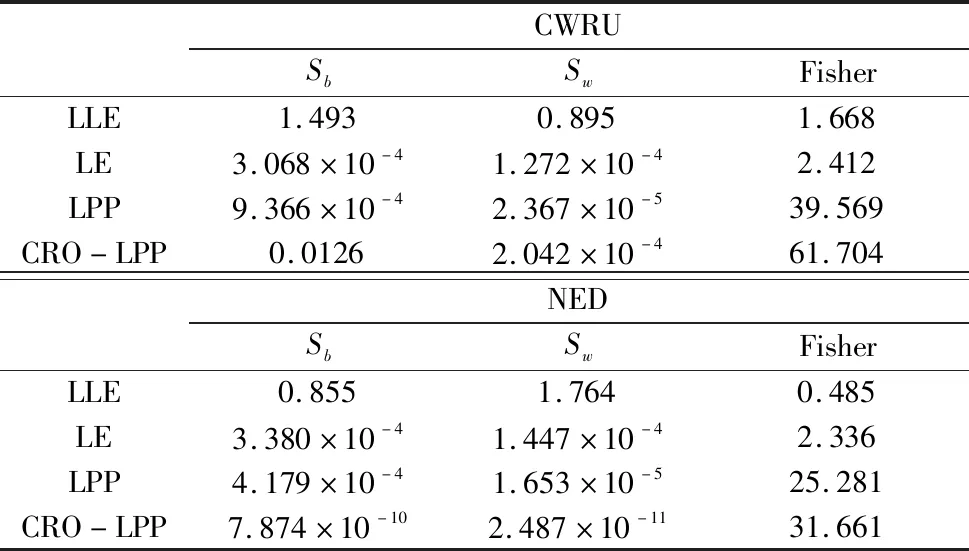
表1 不同算法在两种数据集上的Fisher度量

第三组实验在NED数据集上将对比使用不同距离度量方法与相关性Rank-order距离度量进行比较，如图7所示。在三维空间中，在余弦距离度量的度量下，算法所提取的故障特征重叠，分离性较差；Manhattan度量和杰卡德相似性度量仅能分离其中部分故障特征，分类效果并不明显；而在相关性Rank-order距离度量中，所提取的故障特征均表现出了较好的分离和聚类性能，优于其他度量方法，适合特征提取，进而证明了改进算法的有效性。

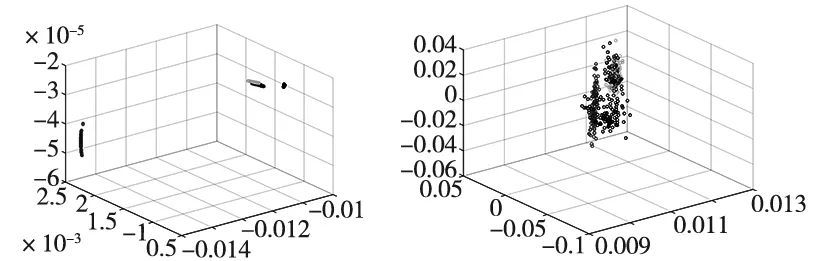
(a) LPP算法Manhattan距离 (b) LPP算法余弦距离

在第四实验中，本文将对改进算法的特征提取性能进行验证分析。分别在CWRU数据集和NED数据集中选择80个数据样本进行训练，剩余20个样本作为测试集分别使用局部算法进行特征提取，最后由KNN分类模型测试特征正确识别精度，并求其四次平均作为最后测试结果，如图8所示。在图中实验的局部算法中，LTSA算法所提取特征识别精度较差，而CRO-LPP算法提取的特征识别率均高于其他算法，更进一步证明了算法对轴承故障特征有较好的提取性能。

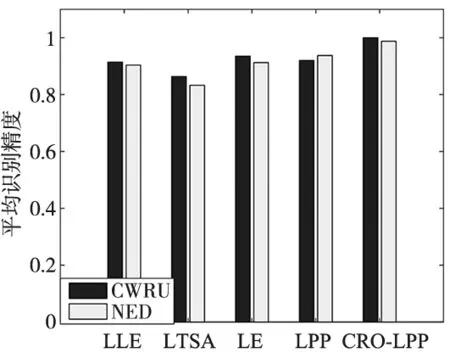
图8 算法在数据集上正确识别率

5 结束语

本文提出了一种基于相关性Rank-order度量的局部保持投影算法。该算法首先利用相关距离融合Rank-order距离度量样本间的相似性，构建了降维模型。该方法极大的提高了原算法相似性度量的准确性，使样本的聚类效果更加明显。通过将该算法应用在两种轴承数据集上，由可视化及识别精度等实验对比验证了所提算法的有效性。同时，未来将进一步对离群点进行研究并进一步优化邻域参数的选择，使得到更好的降维效果。