双挂汽车列车右转弯内轮差分析与改善
巩长伟,张树翠,张欣刚,姚文莉
(1.青岛理工大学 机械与汽车工程学院,山东 青岛 266520; 2.青岛理工大学 理学院,山东 青岛 266520)
近年来,大型汽车运输在我国的公路运输中占有越来越重要的地位,但由于国内外大型汽车在右转弯过程中会产生内轮差且普遍不受信号灯的调控,所以大型货车右转弯事故频频发生,成为致人死亡最多的交通事故类型,据杭州市交警部门统计,杭州市2019年重型货车右转弯事故占重型货车交通事故死亡数的28.76%,2020年上升到33.33%[1]。双挂汽车列车作为大型货车运输的主要车辆之一,相比于普通半挂车,车辆单元多,车身较长,所以双挂汽车列车在右转弯运动过程所需空间更大,时间更长,其仿真结构如图1所示。

图1 双挂汽车列车仿真结构图
因此,对其右转弯的运动轨迹和内轮差进行研究分析,对于提高汽车行驶的安全性具有重要的意义。李英帅等提出了一种铰链车右转内轮差区域范围的确定方法[2]。王珂等分析了不确定性对车辆轨迹预测的影响机理及控制方法[3]。鄢勇飞等分析了车辆内轮差在典型车辆轴距、路缘石转弯半径情况下的变化规律[4]。石永金等对拖拽多台挂车的汽车列车的最小转弯半径进行了分析计算[5]。刘斐等对比分析了道路几何参数对双挂汽车列车在弯道行驶时安全车速阈值的影响[6]。张卫华等基于汽车转弯原理建立了半挂车转弯盲区障碍物危险判别轨迹模型[7]。王清洲等探究了半挂汽车右转过程中轨迹盲区与右后视镜视野盲区的形成过程及其相互关系[8]。周立平等通过定量分析法对内轮差的各种影响因素进行了分析[9]。
在以往对于汽车转弯内轮差的研究中,大多数的研究对象都是小汽车和半挂车,很少有人双挂汽车列车的研究,而且采用建模方法都为传统的运动学建模方法,少有运用多体运动学方法进行建模,在对车辆单元多和结构复杂的车辆进行运动学建模时,传统运动学建模方法步骤繁琐且易出错。因此,本文将运用多体系统运动学建立双挂汽车列车右转弯运动学模型,推导其右转弯的运动方程并进行轨迹仿真分析,通过对挂车后轮轴进行主动转向控制,研究车辆内轮差的变化情况。
1 双挂汽车列车运动学建模
双挂汽车列车是由牵引车、一挂车、Dolly和二挂车四部分组成,其中第一节挂车与牵引车之间通过在一定限度内可自由转动的牵引鞍座相连接,第二节与第一节挂车之间通过Dolly相连接。将大地看作为零号物体,并建立绝对坐标系(g1,g2),其中g1表示横向,g2表示纵向。假设汽车的外部形态不发生变化,则可将车辆整体看作为3个刚体通过两个平面旋转铰相连接,其中牵 引车,一挂车和二挂车分别看作1号、2号和3号刚体,在各个刚体上建立连体基,i=1,2,3。将牵引车、一挂车和二挂车之间的旋转铰看作1号铰和2号铰,并分别建立内外接铰坐标系,j=1,2,3,4。各个车辆单元的夹角表示以及具体运动学建模示意图如图2所示。
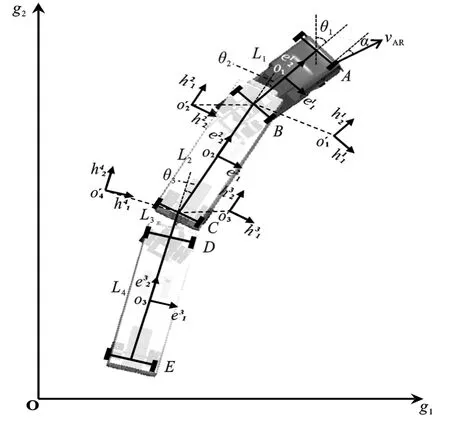
图2 双挂汽车列车双轨运动学模型示意图
2 双挂汽车列车右转弯运动方程求解
2.1 车辆各车轮位置矢量方程求解
双挂汽车列车各个车轮右转弯的运动过程在绝对坐标系可分解为位置平动和姿态转动两个过程,将上述两个过程进行矢量合成,就可得到各车轮运动后的具体位置,其公式如式(1)所示,具体示意图如图3所示。
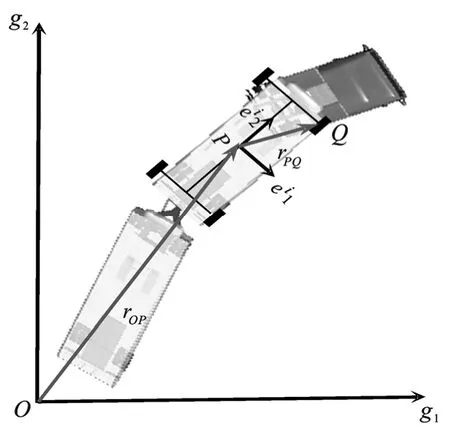
图3 双挂汽车列车运动矢量示意图
式(1)中,rOP为位置平动;rPQ为姿态转动。
2.2 坐标系转换矩阵系数求解
根据双挂汽车列车多体系统建模示意图可知零号物体、1号、2号和3号刚体依次通过垂直于地面的平面旋转铰相连,且夹角分别为θ1、θ2、θ3。根据多体运动学理论可得各刚体连体基坐标系与绝对坐标系转换关系矩阵系数为
式(2)、式(3)中,当j=1时,Aj0=A(j+1)j;当j=2,3时,Aj0=A(j+1)jA(j-1)0,cj=cosθj,sj=sinθj。
2.3 各个车辆单元车轮运动方程求解
2.3.1 1号刚体各车轮轨迹求解
根据多体系统运动学可知各车轮在总体坐标系的运动可分解为其所在刚体连体基原点的平动和车轮绕连体基原点的转动两个过程,已知A轮轴右前轮初始速度vAR,通过速度投影定理可以求得1号刚体连体基原点P1的速度v1,其质心速度与方向的夹角a1,与g2方向的夹角为θ1,故基点P1在绝对坐标系的运动关系式为
式中,下标AL和AR代表A轮轴左侧和右侧车轮,其他轮轴左右侧车轮表示方法与此相同。
2.3.2 2号刚体各车轮轨迹求解
基于上述分析可知1号刚体为2号旋转铰的内接物体,根据几何关系可得2号旋转铰在绝对坐标系的位置坐标GK2。由于( )1 112h,h和( )2 212h,h坐标系原点固结在同一个点上,故原点运动轨迹相同,具体关系式如下:
已知2号旋转铰外接铰坐标系原点在绝对坐标系的运动轨迹GK2,由几何关系可知2号刚体连体基原点P2在铰坐标系的位置坐标,相加可得基点P2在绝对坐标系的运动轨迹GP2。同理可知2号刚体各车轮在连体基的位置坐标,通过转换矩阵计算并与GP2相加便可得到各车轮在绝对坐标系的位置坐标,具体关系式如下:
2.3.3 3号刚体各车轮轨迹求解
根据几何关系可知3号刚体连体基原点P3在铰坐标系的位置坐标,通过转换矩阵计算并与GK4相加可得到其在总体坐标系的运动轨迹GP3。同理可知3号刚体各车轮在连体基得姿态位置坐标,通过转换矩阵计算并GP3相加,可得其在绝对坐标中的位置坐标,以上具体关系式如下:
2.4 其他参数求解
根据上述模型可知,θ1表示为1号刚体连体基坐标轴方向与绝对坐标轴g2方向的夹角;θ2表示2号刚体连体基坐标轴与1号刚体连体基坐标轴的夹角;θ3表示3号刚体连体基坐标轴与2号刚体连体基坐标轴的夹角,具体关系如下:
根据多刚体角速度叠加原理可得
对上述方程进行求解可得θ1、θ2、θ3。
3 双挂汽车列车右转弯轨迹仿真分析
3.1 车辆右转弯各车轮轨迹仿真结果
首先设置仿真工况,路段选用平缓公路,设置转弯方向为右转弯且转角为90°,当t=0时,α=8°,VAR=5 m/s,g1AR=1,g2AR=2,θ1、θ2和θ3均为0,转弯过程中θ1≤90°,其他结构参数具体如表1所示。根据上述结构分析可知双挂汽车列车共有5个轮轴,在右转弯的工况中各轮轴的右 车轮作为内侧车轮,根据上述公式对各个轮轴的右侧车轮轨迹进行仿真,仿真结果如图4所示,各个轮轴的右侧车轮轨迹均存在内轮差,其中A、B与C、D轮轴右侧车轮内轮差较小,B、C和D、E轮轴右侧车轮内轮差较大。对于整体分析而言,以A轮轴右侧车轮作为参照,其他轮轴越靠近双挂汽车列车尾部,其内轮差越大,其中E轮轴与A轮轴的右侧车轮内轮差最大。

图4 双挂汽车列车右转弯各车轮运动轨迹图
3.2 挂车后轮轴主动转向的影响
3.2.1 第一节挂车后轮轴主动转向
假设C轮轴车轮主动转向角与22e的夹角大小为β=Kα,转角方向与牵引车转角方向相反[10],根据上述分析模型可知相比于未对C轮轴施加主动转向控制,变化量及其具体关系式如下:
当只对挂车后轮轴右侧车轮运动轨迹变化情况进行分析,由于C轮轴和D轮轴距离较短,故忽略D轮轴车轮的运动轨迹,仅对A、B、C、E轮轴的运动轨迹进行仿真分析,当K=1时,仿真结果如图5示,A轮轴和B轮轴各车轮的运动情况均不受C轮轴主动转向的影响,C轮轴和E轮轴各轮运动轨迹均向弯道外侧方向具有明显偏移,与A轮轴和B轮轴运动轨迹的差值明显减小,车辆整体的内轮差也变小。
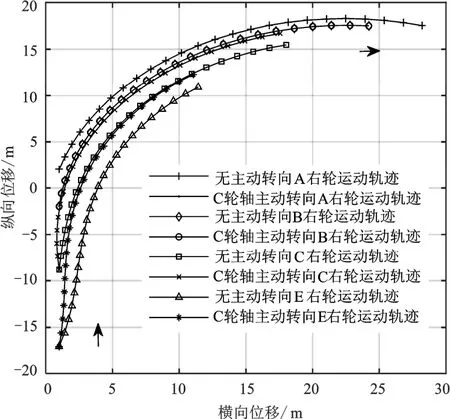
图5 C轮轴主动转向时A、B、C、E各车轮运动轨迹图
3.2.2 第二节挂车后轮轴主动转向
同样只对挂车后轮轴右侧车轮运动轨迹进行分析,忽略D轮轴的运动轨迹,结果如图6所示,当K=1时,A、B和C轮轴各车轮运动轨迹不变,E轮轴各轮运动轨迹均向弯道外侧偏移,与前轮轨迹的差值明显减小,车辆整体的内轮差变小。当K取不同数值时,仿真结果如图7所示,随着K值的不断增大,E轮轴车轮轨迹向外偏移,与A轮轴车轮的轨迹差值逐渐减小,当K>1时,虽然车 辆的内轮差会减小,但由于转向角度过大,会使车辆的侧向力增大,降低汽车行驶的横向稳定性,所以挂车主动转向的角度需要设定在适当的范围内。
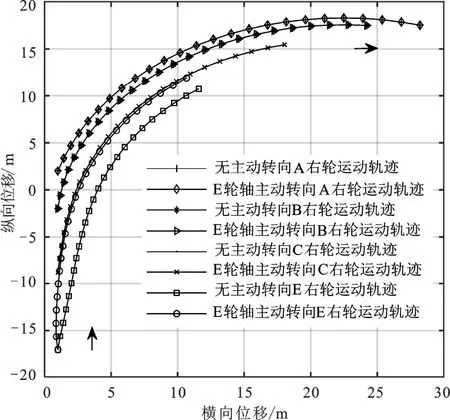
图6 E轮轴主动转向时A、B、C、E各车轮运动轨迹图
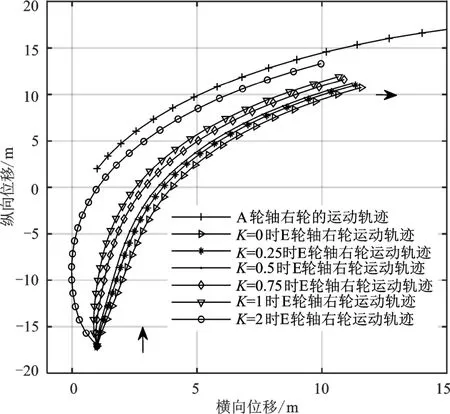
图7 当K取不同值时A、E轮轴车轮运动轨迹图
4 结论
1)双挂汽车列车在右转弯的过程中,其挂车后轮的运动轨迹较牵引车前轮向弯道内侧偏移,产生内轮差,并存在尾部放大效应,越靠近车辆尾部其内轮差越大。
2)在低速工况下控制第一节或第二节挂车后轮轴主动转角方向与牵引车前轮转角方向相反,均可以明显减小双挂汽车列车右转弯时的内轮差。
3)控制挂车后轮轴主动转向的转角要在适当范围内,转向角度过大会降低汽车行驶的横向稳定性,易使车辆发生失稳。

