某汽车盘式制动器制动噪声分析

何代澄

（南方天合底盘系统有限公司，重庆 402760）

汽车制动器系统产生的噪声会严重影响驾驶汽车的舒适性，进而影响汽车产品的市场竞争力，因此，对汽车开发过程中的制动器系统产生的制动噪声的研究具有重要意义[1-2]。

有限元仿真分析方法可以有效缩短产品开发周期，已广泛应用到汽车及其零部件的开发过程中，以验证产品结构设计的合理性[3-4]。在有限元仿真分析中采用复特征值法，可以有效预测制动器系统发生噪声的可能性，已得到了较多学者的认可[5-8]。

因此，本文主要是基于复特征值法，建立某汽车盘式制动器制动噪声分析的有限元仿真模型，包括从频率、振型、负阻尼比、模态参与系数、模态应变能等仿真结果进行制动器制动噪声分析，为汽车盘式制动器系统的噪声、振动与声振粗糙度（Noise, Vibration and Harshness, NVH）开发提供理论依据。

1 仿真分析方法

1.1 几何模型

本文基于UG软件进行三维几何设计建模，建立的某汽车盘式制动器系统的三维几何模型如图1所示，包括制动盘、制动卡钳、钳体支架、活塞、制动块、消音片、回位弹簧、导向销、轮毂轴承、转向节等零部件。

图1 几何模型

1.2 仿真模型

本文基于ANSYS Workbench仿真分析平台进行仿真分析建模和求解计算，并采用HyperView软件进行仿真结果后处理查看，建立的某汽车盘式制动器制动噪声分析的有限元仿真模型如图2 所示。在划分有限元网格前，需对该汽车盘式制动器系统三维几何模型中的一些细小特征进行适当的简化，从而提高有限元网格的单元质量，进而缩短有限元仿真模型的求解计算时间，提高求解计算的收敛性和效率。此外，制动块的摩擦材料采用各向异性材料，其仿真参数如表1所示，其余零部件均采用线弹性材料，其仿真参数如表2所示。

图2 仿真模型

表1 摩擦材料参数

表2 零部件材料参数

1.3 分析设置与求解控制

根据制动器系统的装配关系，定义适当的各零部件间连接关系，其中制动盘与摩擦块材料、摩擦块背板与消音片、消音片与活塞及制动卡钳间的接触定义为摩擦接触，钳体支架与导向销、轮毂轴承与转向节及制动盘间的接触定义为绑定接触。制动盘和制动块的摩擦系数设置为0.4，对制动卡钳活塞腔和活塞分别施加制动液压力，释放制动盘的旋转自由度，同时分别约束转向节的摆臂孔、转向孔和减振孔的3个平动自由度。

在ANSYS仿真软件中采用APDL命令流的方式，进行某汽车盘式制动器系统的复特征值模态分析，包括：1）定义制动盘和制动块的摩擦接触对；2）建立系统的应力-应变状态及接触压力分布结果；3）对制动盘施加轴向旋转运动，形成非对称刚度矩阵；4）运用完全非线性摄动模态分析法，并采用非对称模态求解器进行求解计算，求解频率范围为0～16 kHz。

2 仿真结果及分析

2.1 复特征值

图3为某汽车盘式制动器系统的复特征值分析结果，其中横坐标是复特征值的虚部，为振动频率；纵坐标是复特征值的实部，为模态的稳定系数，当实部为正值时则表明该阶模态不稳定，易产生噪声。从复特征值计算结果可以看出，频率为5973 Hz、7170 Hz、7355 Hz、8337 Hz、9764 Hz、9870 Hz、10613 Hz、11435 Hz、11708 Hz、 11786 Hz、12049 Hz时制动器系统的复特征值实部为正，表明该制动器系统存在着这11阶不稳定模态频率，其对应的复特征值实部大小分别为30.4、7.5、16.2、45.5、1.3、8.1、6.1、36.7、4.6、25.8、7.0。由此可得出，频率在8337 Hz时该汽车盘式制动器系统的复特征值实部为最大值45.5，表明该汽车盘式制动器系统在8337 Hz频率附近发生制动噪声的可能性最大。

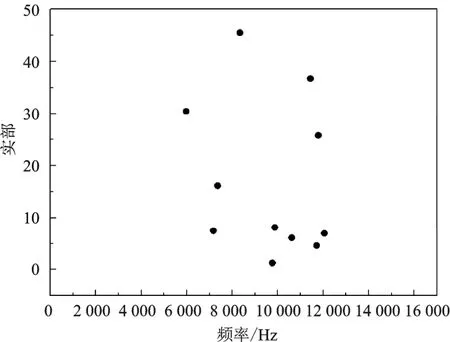
图3 复模态计算结果

2.2 复模态振型

图4 为某汽车盘式制动器系统不稳定模态频率为8337 Hz时的模态振型，该阶模态被认为是最有可能引发该制动系统噪声的一阶模态。

图4 复模态计算得到的不稳定模态振型

2.3 负阻尼比

图5 为某汽车盘式制动器系统的负阻尼比结果，可以看出该制动器系统出现负阻尼的频率分别为5973 Hz、7170 Hz、7355 Hz、8337 Hz、9764 Hz、9870 Hz、10613 Hz、11435 Hz、11708 Hz、 11786 Hz、12049 Hz，对应的负阻尼比分别为-0.5097%、-0.1043%、-0.2198%、-0.5456%、-0.0130%、-0.0824%、-0.0577%、-0.3210%、-0.0395%、-0.2190%、-0.0579%。由此可得出，频率在8337 Hz时该汽车盘式制动器系统的负阻尼比为最小值-0.5456%，负阻尼的出现会导致系统的振荡增大，表现为一个发散的不稳定系统，同样表明该汽车盘式制动器系统在8337 Hz频率附近发生制动噪声的可能性最大。

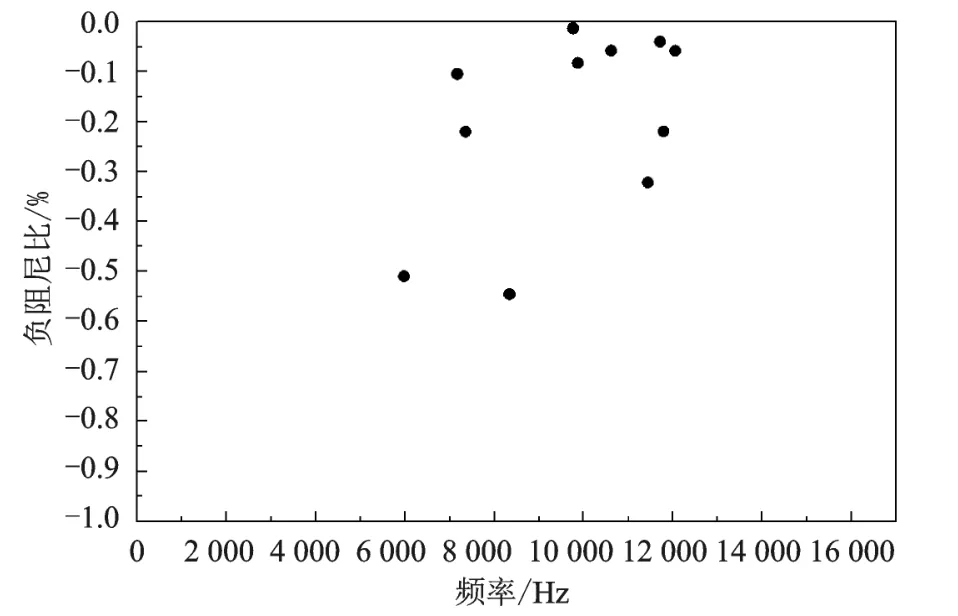
图5 负阻尼比

2.4 模态参与系数

参与系数表示某阶模态在某个方向上的质量运动，可以用来表征在某一特定方向上某个振型在多大程度上参与了振动。图6为某汽车盘式制动器系统不稳定模态频率为8337 Hz时在X、Y、Z方向的模态参与系数，可以看出，该汽车盘式制动器系统在Z方向的参与系数值最大，表明该汽车盘式制动器系统在Z方向受到动载荷作用时，该汽车盘式制动器系统的结构振动响应越大，进而引发噪声的可能性越大。

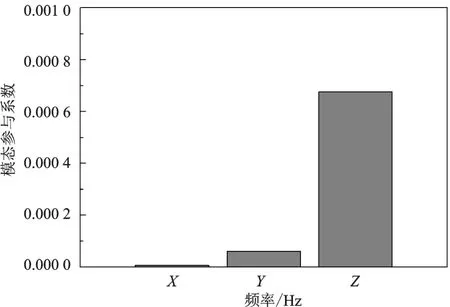
图6 模态参与系数

2.5 模态应变能

为了得到制动器系统的能量分布情况，本文对某汽车盘式制动器系统进行了模态应变能分析。首先，计算了整个制动器系统的总应变能，以及分别计算出制动盘、制动卡钳、钳体支架、活塞、制动块、导向销、轮毂轴承、转向节等零部件各自的应变能。图7为不稳定模态频率为 8337 Hz时对应的模态应变能云图，可以看出， 8337 Hz时制动盘为整个制动器系统结构中吸收能量最集中的部位。

图7 模态应变能云图

进一步计算出各个零部件的模态应变能与整个制动器系统的总应变能的比值，确定该阶不稳定模态下各个零件的贡献程度，为制动器系统的结构设计提供参考。图8为不稳定模态频率为 8337 Hz时各个零部件的模态应变能与整个制动器系统的总应变能的比值，可以看出，8337 Hz时制动盘和制动块的应变能比值较大。

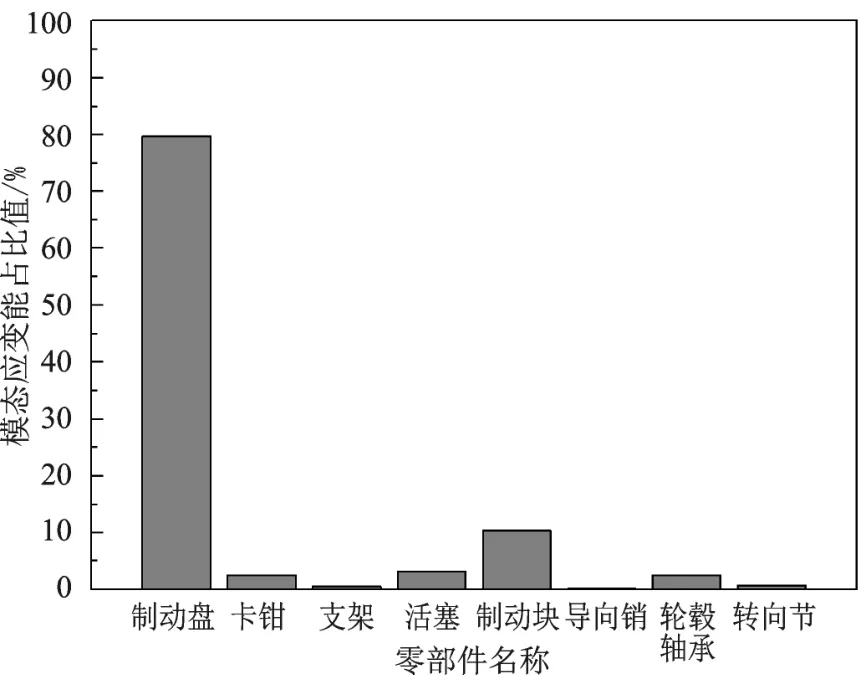
图8 模态应变能占比值

鉴于制动盘和制动块的应变能比值较大，进一步提取出该汽车盘式制动器系统不稳定模态频率为8337 Hz时制动盘与制动块的模态振型，如图9所示，可以看出，制动盘和制动块之间发生模态耦合。

图9 制动盘与制动块不稳定模态振型

由此可得出，8337 Hz时该制动器系统的不稳定模态，主要是由于制动盘和制动块之间发生模态耦合引起的。因此，通过改进制动盘或制动块的结构，包括改进制动盘的散热筋尺寸参数、制动盘厚度、制动块背板结构、制动块背板厚度等，避免制动盘和制动块之间在8337 Hz时发生模态耦合，可以有效消除该阶不稳定模态，从而防止该制动器系统发生制动噪声。

3 结论

1）某汽车盘式制动器系统频率在 8337 Hz时，复特征值实部为最大值45.5，负阻尼比为最小值-0.5456%，均表明在8337 Hz频率附近发生制动噪声的可能性最大。

2）某汽车盘式制动器系统频率在8337 Hz时，Z方向的参与系数值最大，表明在Z方向受到动载荷作用时，该汽车盘式制动器系统的结构振动响应越大，进而引发噪声的可能性越大。

3）某汽车盘式制动器系统频率在8337 Hz时，制动盘和制动块的应变能比值较大，且该不稳定模态主要是由于制动盘和制动块之间发生模态耦合引起的。