移动荷载下功能梯度梁的快速力学算法研究★

石智锋,姜志杰,姚 达,顾夏炜

(南通大学交通与土木工程学院,江苏 南通 226019)

1 概述

在工程实际应用中,经常会出现移动载荷的情况,如汽车过桥、座椅电梯运行以及轨道运输等,一般这些问题可以视为移动荷载作用下梁的横向振动响应问题。这时的载荷作用位置沿行进方向随时间发生变化,在控制方程中常借用狄拉克函数来表达,从而给力学求积带来了一些麻烦。同时,随着人们生产和生活需求的不断提升,不断地对承受移动荷载的梁也提出了更高的性能要求。功能梯度梁(Functionally Graded Beam,FGB)就是一种为满足在极限环境下能反复地正常工作而发展起来的一种新型功能材料梁。通过材料设计,可以使其功能、性能随内部位置的变化而变化,从而使优化构件的整体性能得以满足，所以功能梯度梁的应用越来越广泛。而当移动载荷遇到功能梯度材料梁,两者在力学计算中都具有一定地挑战性,如何通过快速力学计算,优化此类产品设计是一个非常重要且亟需解决的问题。

目前,移动荷载作用下梁的响应研究已经得到了很多学者的关注。文献[1]采用多尺度法和Galerkin法分析移动载荷作用下 Euler 梁的频率响应曲线。文献[2]研究了梁的跨长对移动荷载下梁稳态响应的影响,所得结论有助于更深入地理解移动荷载作用下有限长梁的响应以及梁结构影响线问题。更有研究者[3]提出了一种计算单个移动质量作用下两层简支梁动力响应的简便方法,并分析了质量大小、移动质量速度、温克尔层弹簧的刚度和阻尼对系统动力响应的影响。龚云轩等[4]基于铁木辛科梁理论,采用连续体传递矩阵法计算了阶梯梁的受迫振动响应。文中研究了转动效应的影响因素，指出移动载荷的质量相较于移动速度和加速度而言,是最主要的转动效应影响因素。当移动载荷的质量较大时,必须要考虑速度和加速度引起的是转动惯性的影响。闫镜宇等[5]利用奇异函数推导了简支梁在移动载荷作用下的挠曲线微分方程,并研究了横向强迫振动下简支梁的响应问题。指出随移动载荷的速度增大,将使简支梁的挠度最大值和位移最大值呈抛物线形分布。而对于指定截面而言,最大静挠度和载荷移动速度无关。目前,基于功能梯度材料梁的研究相对不多,且对于物性参数的变化主要考虑的是沿厚度方向的梯度变化。张靖华等[6]研究了外加集中力沿着梁的轴向移动时功能梯度材料梁的动力响应规律。基于模态叠加法和经典梁理论,解析求得简支梁的基础频率和振型,并研究了共振特性及其影响因素。

以上研究表明,移动载荷下结构的响应问题不管是理论研究还是数值求解均受到了国内外学者的广泛关注,尤其是对材料性能梯度变化的功能梯度梁而言,准确预测移动荷载作用下结构的振动响应具有重要的理论意义和工程实用价值。但是对于大多数动态响应问题,分析计算的关键在于选取合理的时间步长。时间步长太小会浪费计算资源,而时间步长太大也将使得高阶模态产生误差。因此,基于选取合理的时间步长的考虑,本文将采用弱式求积单元法进行研究。

弱式求积单元法最初是由Striz等[7]提出的,经过多年的发展已逐渐成为一种全新的数值解法来求解初边值问题。由于在推导单元矩阵时采用了微分求积法的权系数公式,这样可以得到节点数可以变化的单元矩阵的显式计算式,便于编程的同时也提高了数值计算的效率[8]。本文借助弱式求积单元法的快速高效的优异特点,对移动载荷下功能梯度梁的动态响应进行力学算法研究。只要集中载荷作用在结点处,就可以很方便的采用弱式求积单元法进行求解。

2 基本公式

考虑图1所示的欧拉-伯努利功能梯度梁,受移动集中载荷作用。图1中梁的长度、移动集中荷载、荷载的移动速度以及时间分别用L，P，v和t来表示,而h和b则分别代表梁的厚度以及宽度。材料性能沿梁高梯度变化趋势和文献[9]一致,采用幂指数的形式。由于时间变化,集中载荷的作用点也不断变化,所以需要先根据等效变换的做法,把集中载荷等效到各个结点上。

假设解耦后的位移场如下：

(1)

其中,u*(x,z,t)和w*(x,z,t)分别是轴向和横向位移分量,u*(x,e,t)=0,e为几何中面和物理中面间的距离。

功能梯度材料欧拉梁的弯曲应变能可以写为：

(2)

研究中基于欧拉梁理论,忽略转动惯量和耦合的影响,功能梯度材料梁的动能写为：

(3)

外载荷P作的功可以写为：

W=Pw(vt) (0≤t≤L/v)

(4)

研究基于高效的弱式求积单元法,采用一个欧拉梁单元进行计算。为了使后期计算步长最长且合理,因此选用扩展的切比雪夫(E-Chebyshev)结点。图2给出了一个11结点的弱式求积欧拉梁单元的示例。

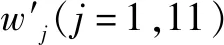
(5)

其中,[m]和[k]分别为欧拉梁单元的质量矩阵和刚度矩阵；{f(t)}为载荷向量。之后采用中心差分法求解该二阶常微分方程组,囿于篇幅,此处不再赘述。

3 算例和讨论

功能梯度材料梁的跨中位移和弯矩的动态放大因子为Wam和Mam定义如下[10]：

(6)

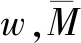
图5给出了S-S功能梯度材料梁的跨中弯矩的动态放大因子Mam。单元节点数仍从11变化到21。α取值为0.25，对比发现，收敛性方面，弯矩的收敛性要比位移的略低。从这一角度看，和常规有限单元法求解的应力和位移在精度方面的结论是一致的。也再次说明了，本质上，弱式求积单元法也是一种高阶有限元方法。

图6,图7给出了两端固定(C-C)时，跨中位移和弯矩的动态放大因子Wam和Mam。因为解析解无法获得，所以采用改进的微分求积法结果来进行比较。可以看到，随着参数α的变化，两种方法中，Wam彼此相近，而Mam也几乎完全相同。表明N-节点弱式求积欧拉FGB单元可以用较少的结点快速得到准确的位移和弯矩。

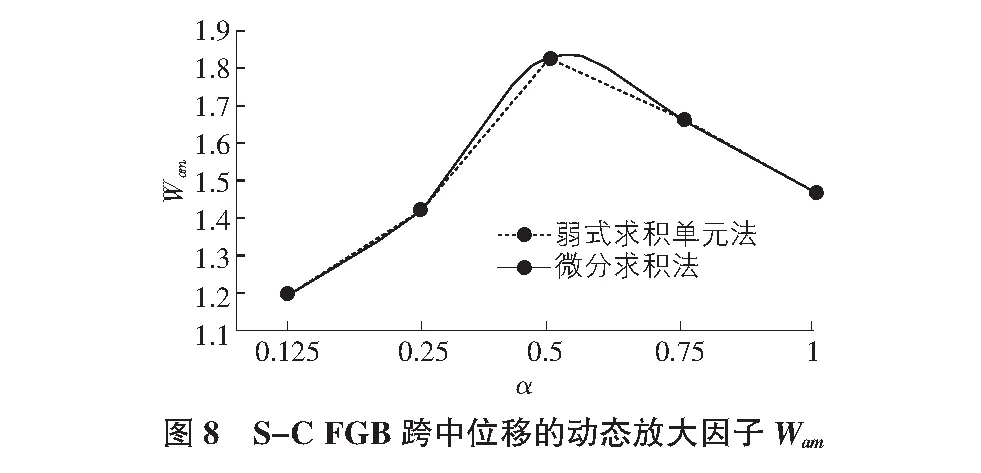
而对于一端简支，一端固支的情况，从图8,图9也可以得到相似的结论。弱式求积单元法的计算结果和微分求积法的几乎完全吻合，但由于边界条件不同，跨中位移和弯矩的数据结果也不同。随着参数α的增大，跨中位移和弯矩大致都呈先增大后减小的趋势，说明移动速度的影响不可忽略。且不论哪种边界支承条件，同一个参数α下功能梯度梁跨中的Wam和Mam与材料梯度参数均无关。这对工程实践应用来说，就可以借助各向同性材料梁的计算结果，大大减少计算工作量。

4 结语

采用弱式求积单元法可以很方便地进行功能梯度材料梁的动态力学分析,结点数目较少时也可以快速获得准确的计算结果。移动载荷作用在功能梯度梁上时,梁的动态响应与两端的支承条件以及点载荷移动的速度有较大的关系。在固定综合体现点载荷移动速度和材料属性的无量纲参数α下,功能梯度材料梁跨中位移和弯矩的最大动态放大因子与材料梯度参数无关,可以考虑借助各向同性材料梁的结果来计算功能梯度材料梁。