一种可解释的自由文本击键事件序列分类模型
张 畅 韩继红 张玉臣 李福林
(信息工程大学 郑州 450000)
1 引言
随着人工智能技术的飞速发展,人脸等生物特征在身份认证和识别领域得到广泛的应用。研究表明,人敲击键盘的“节奏”可以作为身份认证和识别的行为特征[1]。通常把按键事件发生的时间间隔作为击键行为特征,一般包括从前一按键释放到后继按键按下的时长UD time、从前一按键按下到后继按键按下的时长DD time(或称digraph)、从前一按键释放到后继按键释放的时长UU time、按键从按下到释放的时长Hold time、n(n≧2)个按键事件从第1个按键按下到第n个按键按下的时长n-graph等。击键行为研究一般分为固定文本和自由文本两大类,如果击键事件序列对应文本内容和长度都相同,属于固定文本研究;如果内容和长度不确定,则属于自由文本研究。
人们研究击键行为已有40多年。期间,固定文本研究文献较多,取得了很好的分类效果,而自由文本研究的文献偏少,且分类效果一直不佳[2]。近期,Acien等人[2]用孪生网络模型大幅提升了自由文本击键事件序列的分类效果。本文在Acien的工作的基础上展开深入研究,探索分类效果好且具有可解释性的模型。
自由文本击键事件序列因为键值不确定、长度不一,所以无法得到像固定文本一样“整齐”的特征向量。常见的自由文本击键事件序列特征有:(1)以按键组合的n-graph均值为特征[3–6];(2)以基于n-graph均值的按键或按键组合的排序为特征[7,8];(3)以分组组合的用时均值为特征,例如把键盘划分成左手区、右手区和空格3组[9,10],以这3组按键事件的时间间隔为特征,或者按元音、辅音、标点、功能键等划分按键[11],以元、辅音等分组按键事件的时间间隔为特征。上述方法中,文献[5]和文献[6]在Clarkson II自由文本数据集获得了15.3%和7.8%的等错误率(Equal Error Rate, EER),但得到这样的结果需要至少200个digraph的测试样本和10000个digraph 的训练样本,因此不适用于短自由文本击键事件序列的分类。因为自由文本击键事件序列的特征不“整齐”,很长一段时期,自由文本击键事件序列的分类效果远不及固定文本。
近期该问题有了转机:生成模型POHMM[12]把击键事件序列看作被试者受“积极”、“消极”两种隐状态的影响对键入文本的响应,如果有覆盖全面的训练集,理论上可以消除文本内容差异对分类的影响,但采集这样全的样本数据并不现实。芦效峰等人[13]尝试用卷积神经网络+循环神经网络结构的深度神经网络模型做自由文本击键事件序列的分类,在Buffalo 数据集中使用相同键盘的75个被试者的数据上,取得了3.04%的EER。作者声称其研究不足之处在于使用的数据量小。另外,这种方法解决的是闭集识别问题。Acien等人[2]用Aalto University自由文本数据集[14]的6万多被试者的数据训练基于长短时记忆网(Long-Short Term Memory,LSTM)的孪生神经网模型TypeNet,在剩余10多万被试者的数据上测试,获得了2.2%的EER,分类效果明显优于POHMM。Morales等人[15]在Acien工作的基础上,提出用SetMargin Loss训练TypeNet模型。和Acien采用的Contrastive loss和Triplet loss不同,SetMargin Loss使得同类特征序列集围成的面积小,而不同类特征序列的间距离大。该做法使TypeNet模型能够更好地适应类内变化,取得了1.85%的EER。
2 研究思路
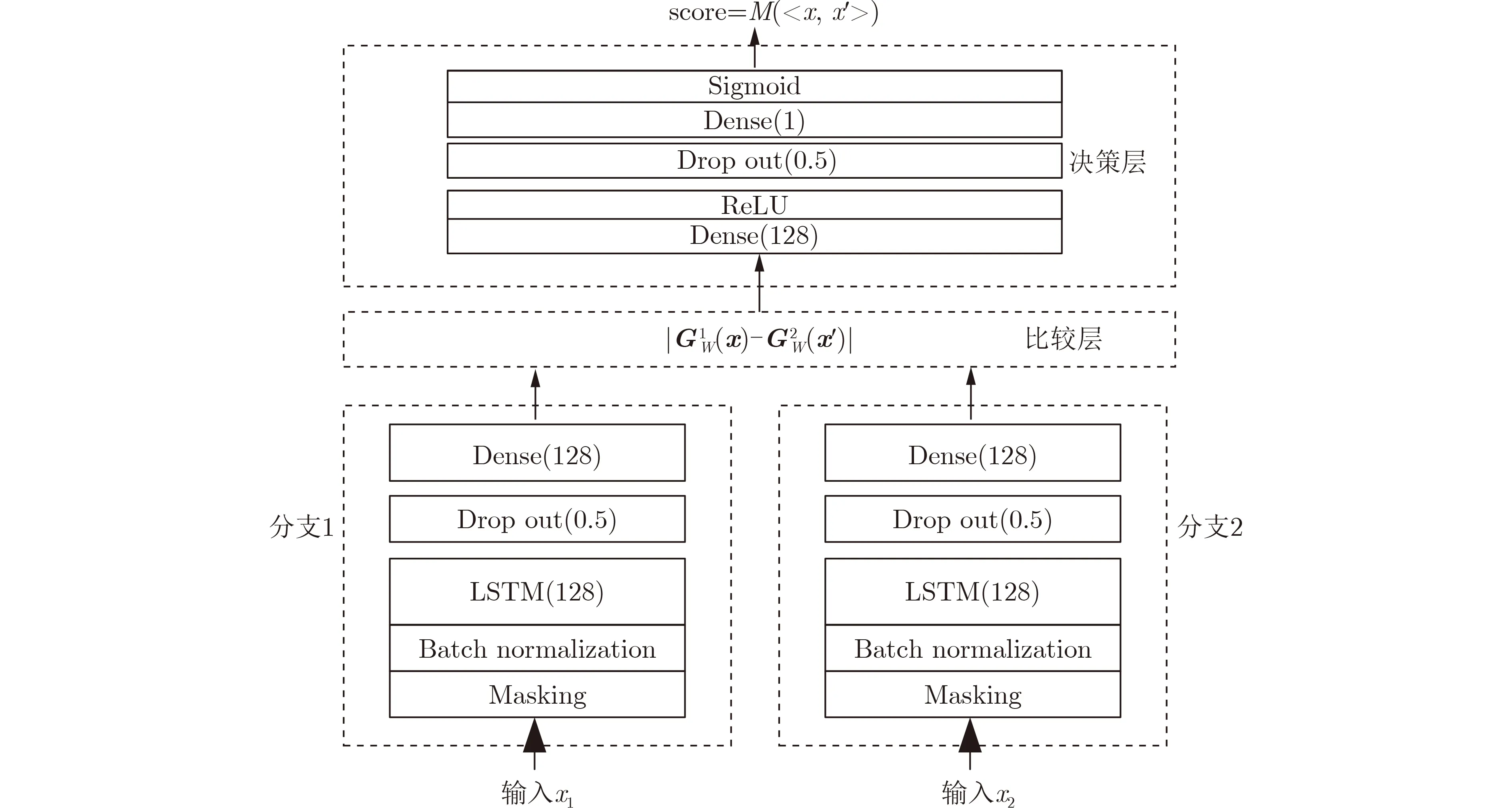
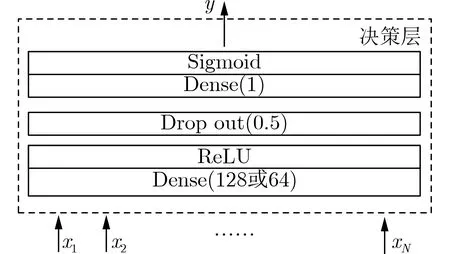
Acien和Morales的实验结果验证了TypeNet网络结构的有效性,即用双层LSTM将击键事件序列对应的特征序列映射到表征空间(embedding space),基于孪生网络结构采用对比学习方法,使得在表征空间上,属于同一人的特征序列的欧氏距离小,不同人的特征序列的欧氏距离大。TypeNet的表征空间是128维,使用欧氏距离度量表征向量(embedding)的相似度,所以表征空间的维度缺乏可解释性。本文用多层感知机替换TypeNet模型中的对比损失函数,来度量表征向量的相似度。具体做法是:把孪生网络模型的分支输出的表征向量差的绝对值作为多层感知机的输入,多层感知机输出作为孪生网络模型输入特征序列对的相似度量值,激活函数为sigmoid,采用交叉熵损失函数训练模型。为了解释表征向量,把多层感知机的输入X(即表征向量)的元素xi作为自变量,输出y作为因变量,用多元多项式模拟多层感知机的输入X和输出y之间的关系y=f(X)=f(x1,x2,...,xN)。根据多元多项式f分析X各维度与相似度量的关系。
3 孪生网络模型
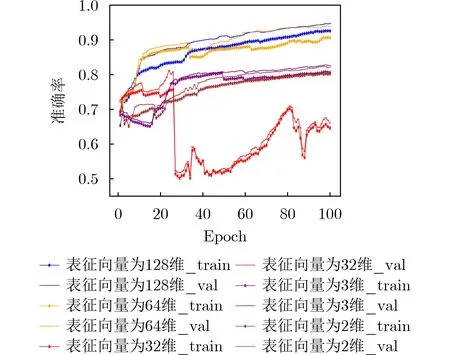
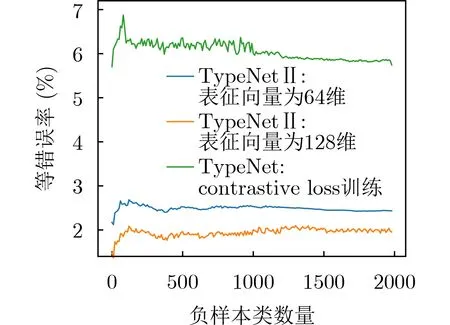
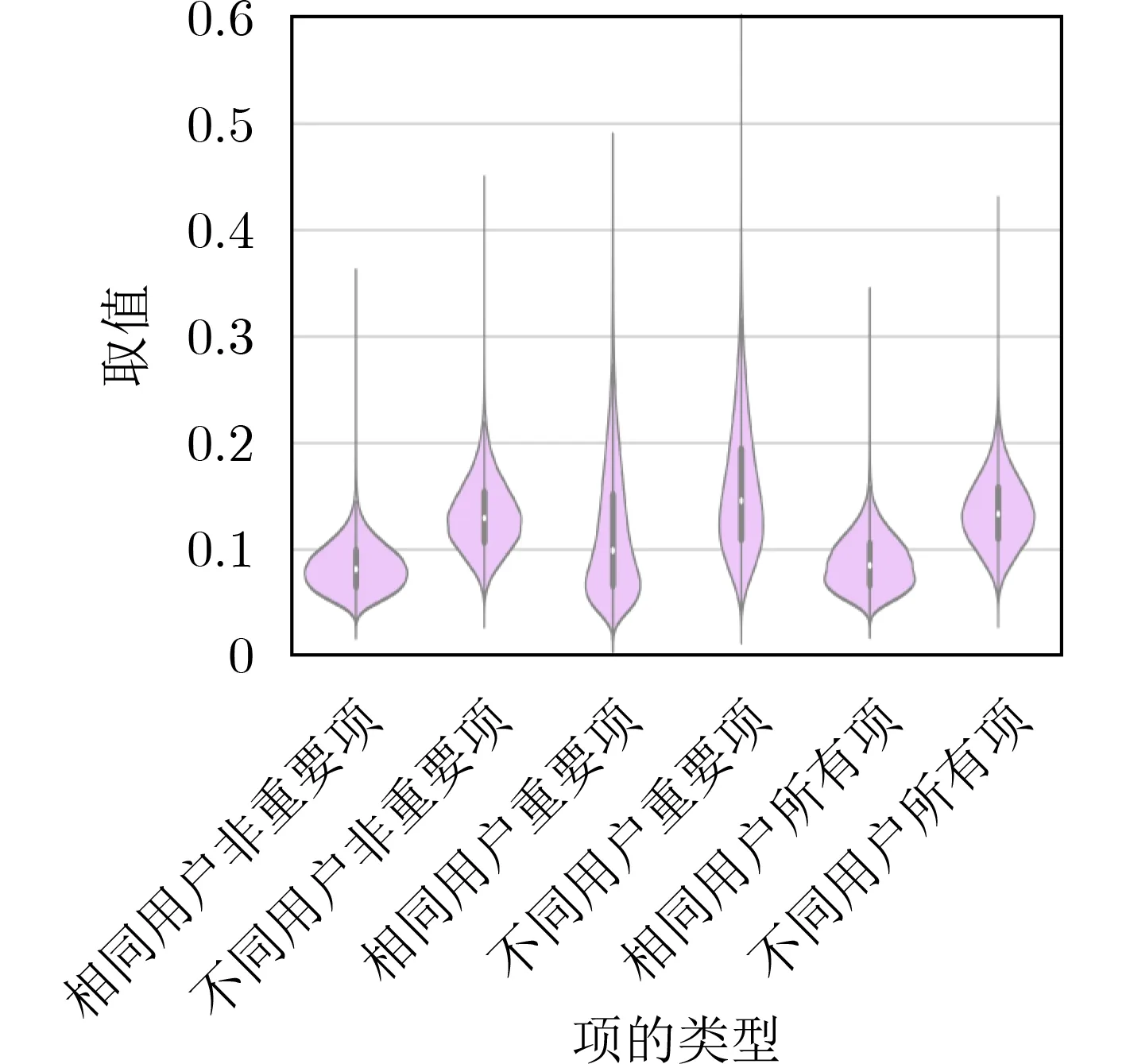
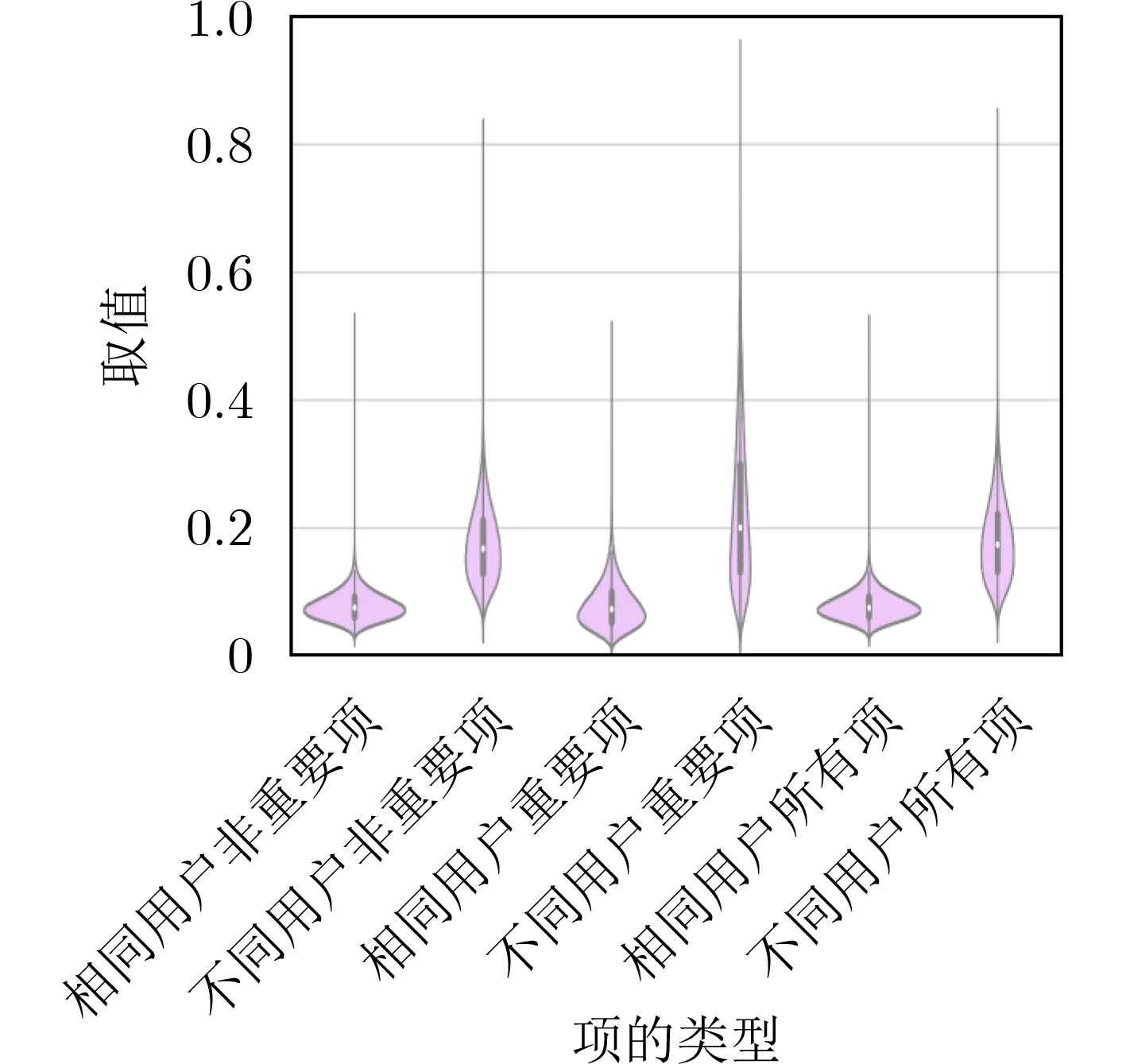
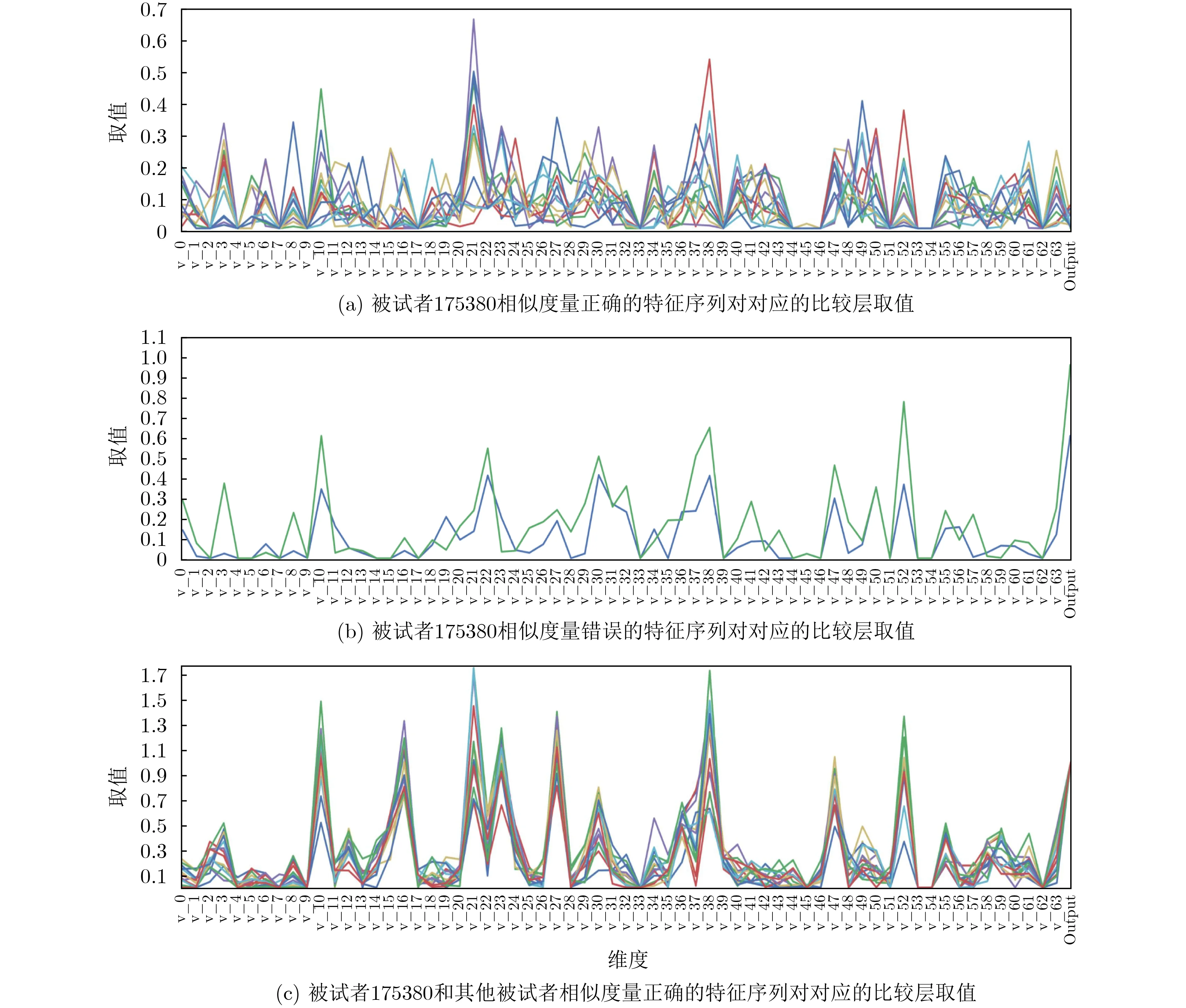
TypeNet模型[2]的分支的输入为长度为M的特征序列。特征序列的元素是一个5元组:<按键值、按键的Hold time、本按键与后一按键的UD time、本按键与后一按键的DD time、本按键与后一按键按键的U U t i m e>。若特征序列长度N>M,则截断丢弃超出长度M的部分;如果N 本文最初尝试用和TypeNet模型一样的分支结构,即两层L S T M,得到的训练效果远不及TypeNet模型,之后转而用单层LSTM网络作分支结构,得到测试准确率超出了用contrastive loss训练的TypeNet模型近5个点。下面介绍改进的模型TypeNet II。 单层LSTM的输出是128维,若不降维处理,分支输出的表征向量也是128维。为了降低模型的复杂度,在确保分类准确率的前提下,应尽量降低表征向量的维度(分支的Dense层的作用类似于bottleneck layer),所以本文也尝试了一些比128小的维度。实验中,表征向量维度取值范围为{128, 64,32, 3, 2}。 为了弄清楚比较层各维度与相似度量的关系,本文用多元多项式模拟决策层(原理如图2所示)。多元多项式的自变量对应于比较层的各维度,因变量是决策层的输出,亦模型的输出。将大量特征序列对输入训练好的模型产生因变量和自变量数据集,在此数据集上用岭回归学习多元多项式f(X)=f(x1,x2,...,xN),根据多项式分析比较层对决策层输出的影响。 图1 TypeNet II的结构 图2 决策层的多元多项式回归模型 和Morales一样,本文用Aalto University自由文本数据集的68000个被试者的数据训练TypeNet II,在剩余数据中选5000个被试者的数据测试分类效果。从Acien和Morales的文献中无法得知这些数据来自哪些具体被试者。本文随机抽取符合上述数量的数据作为训练和测试数据。实验分两部分:实验1训练TypeNet II模型,并和Morales提出的模型的分类效果进行比较;实验2用多元多项式模拟TypeNet II模型的决策层,用参与训练TypeNet II模型的10000个被试者的数据学习得到多元多项式f1,用未参与模型训练的10000个被试者的数据学习得到多元多项式f2, 比较f1和f2的系数以验证多元多项式回归的泛化性,最后结合多元多项式分析比较层与决策层输出的关系。实验代码的地址为:https://github.com/zcmail/TypeNet_II。 图3展示了TypeNet II模型训练过程中的训练(train)和验证(val)准确率。模型输出小于0.5判定输入特征序列对属于同一人,反之,不属于同一人。图4反映表征向量维度为128和64时模型的准确率高,维度为3和2时准确率低,维度为32时准确率最低。表2展示经过100个epoch的训练,采用不同表征向量维度的模型取得的最佳验证准确率。根据图4,本文选择测试了表征向量为128和64维的模型的分类效果。测试时,根据每个被试者的特征模板确定分类阈值(不一定是0.5)。表3展示TypeNet II模型和TypeNet模型的分类效果。可以看出,表征向量为128维时,TypeNet II的分类效果超过了目前已知最好的方法(即Morales的方法[1])。 表1 TypeNet II模型的主要超参数 表2 TypeNet II模型不同表征向量维度对应的最佳训练验证准确率 表3 模型的分类效果 图3 TypeNet II模型的训练和验证准确率 图4 分类效果随负样本类数量的变化情况 表4 两个表征向量维度下P tr上 多元多项式f 不同自由度对应的R2 表5 两个表征向量维度下P tr上多元2阶项式岭回归结果 为了验证在Ptr上 训练得到的多元二项式f的泛化能力,本文在Str以外的10000个被试者的特征序列对数据集Pte上做了同样的工作,得到的多元2阶多项式回归结果如表8—表10所示。综合表6、表7、表9、表10可以得:在Pte上,表征向量为128维的模型的决策层的多元二项式回归系数大于0.5的有16项(表9),这16项和Ptr上学习得到多元二项式(表6)基本一致。由于多元二项式的项多,逐个分析难度大,所以本文把比较层的维度分为两类:把表6的16项对应的维度作主要维度,剩余的为其他维度。同样地,表征向量为64维的模型的决策层的多元二项式回归系数绝对值大于0.4的有7项,除了二次项v18×v19外,这6项和Ptr上学习得到回归式(表7)基本一致,本文把这6项对应的维度作为主要维度。 表6 P tr上表征向量为128维,多元2阶多项式系数绝对值超过0.5的项 表7 P tr上表征向量为64维,多元2阶多项式系数绝对值超过0.4的项 表8 两个表征向量维度下P te上多项式岭回归结果 表9 P te上表征向量为128维,多元2阶多项式系数绝对值超过0.5的项 表10 P te上表征向量为64维,多元2阶多项式系数绝对值超过0.4的项 这里比较分析比较层的主要维度和其他维度对决策层输出的影响。图5和图6是将Str之外10000个被试者的特征序列对分别输入表征向量维度为128和64的TypeNet II模型得到比较层的数值的小提琴图。图中第1、第3、第5列分别属于同一人的特征序列对得到的其他维度、主要维度以及所有维度取值的均值,第2、4、6列分别对应不同人的特征序列对得到的均值。图5和图6表明:(1)属于同一人的特征序列对得到的值要低于不同人的特征序列对得到的值;(2)主要维度取值的均值的分布相对分散。 图5 表征向量维度为128的TypeNet II模型得到比较层的数值的小提琴图 图6 表征向量维度为64的TypeNet II模型得到比较层的数值的小提琴图 为了进一步分析比较层各维度与决策层输出(相似度量)的关系,下面选用表征向量维度为64的模型,分析从Str以外的数据中抽取2个被试者(175380, 179773)的样本对应的特征序列。图7(a)是相似度量正确的被试者175380的特征序列对对应的比较层取值,图7(b)是相似度量错误的被试者175380的特征序列对对应的比较层取值,图7(c)是相似度量正确的被试者175380和其他被试者的特征序列对应的比较层取值。被试者175380的第7和第8个特征序列对的 s core超过了0.96,第6和第7个特征序列对的 s core超过了0.6,这是两个错误的相似度量。和图7一样,图8是被试者179773的比较层取值情况。图8(b)展示被试者179773的第5个特征序列和其他被试者的特征序列的s core为0.08,第14个特征序列和其他被试者的特征序列的s core为0.16,第1个特征序列和其他被试者的特征序列的s core为0.23,这是3个错误的相似度量。图7和图8的横坐标的最后一个刻度是 s core。对比图7(c)和图8(c),除了取值变化的幅度稍大外,两者的线型走势没有明显相似之处,但它们对应的决策层的输出都超过0.95。图7(b)相对于图7(a)取值的幅度变化稍大一些,和图7(c)的线型走势没有相似之处,但图7(b)和图7(c)对应的决策层的输出都超过0.6。图8(b)相对于图8(c)取值的幅度变化稍小,和图8(a)没有明显相似之处,但图8(b)对应的 s core都低于0.5。以上分析表明决策层的输入和输出之间是非线性关系。 另外,图7和图8中,比较层的一些维度取值始终是0,例如,v_33, v_53等,还有一些维度取值绝大多数为0,少许为较小的数(1e-2),例如v_9,v_62等。其原因是分支输出的表征向量的这些维度取值为0或者绝大多数取值为0。 实验1的结果表明,和TypeNet模型的分支不同,TypeNet II模型虽然只用了单层LSTM,但分类效果超过了Acien和Morales提出的方法。模型的表征向量维度是128和64维时,分类效果差别不大,当维度降到32或更小维度时,分类效果出现了明显下降。图7和图8表明模型的表征向量是64维时,部分表征向量维度没有提供对样本分类有用的信息,表明模型的表征向量维度还可以继续压缩。 图7 被试者175380的特征序列对应的比较层和模型输出的可视化 图8 被试者179773的特征序列对应的比较层和模型输出的可视化 实验2的结果表明TypeNet II模型中,特征序列的表征向量差的绝对值可以用来判断特征序列是否属于同一被试者。比较层和决策层的输出呈非线性关系,用多元二项式模拟该关系可达到92%以上的准确率。整体上,多元二项式系数大的项对应的比较层的维度的取值大于其他维度,且分布较为分散。说明这些维度的值对决策层的输出的影响较大。但要注意,多元二项式某项的系数大并不一定意味着该项对应的维度对决策层的影响大,因为有可能该维度值始终为0。 基于孪生网络的TypeNet模型采用欧氏距离度量特征向量在表征空间的相似度。由于表征空间每个维度没有明确含义而缺乏可解释性。和TypeNet不同,TypeNet II的分支使用单层LSTM,用多层感知机度量两个分支输出表征向量差的绝对值体现出来的输入特征序列的相似度,其分类效果超过了现有方法。用多元二项式模拟TypeNet II模型中的多层感知机,尔后基于多元二项式,可以分析多层感知机输入和输出之间的关系,对模型作出的分类判断进行解释。本文下一步可以做以下几个方面的工作:(1)结合一些特殊的击键事件序列样本,解释TypeNet II模型如何消除特征序列的键值和长度差异对分类的影响;(2)尝试用在自然语言任务中取得很大成功的transformer处理特征序列;(3)击键行为特征在一些安全级别较高的领域得到了应用[17],但一般不作为独立的身份认证或识别因子[18],可以将其作为基于口令的认证密钥交换协议[19,20]的安全增强,从而降低口令遭受猜测和字典攻击的风险。3.1 TypeNet II模型




3.2 决策层的多元多项式回归

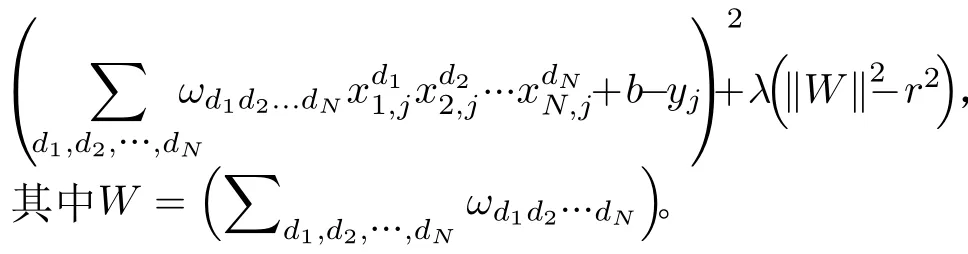
4 实验及结果
4.1 实验1






4.2 实验2








4.3 结果分析

5 结束语

