单有向电磁矢量传感器的参数估计方法
胡毅立 赵永波 陈 胜 牛 奔
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
1 引 言
参数估计是信号处理过程中的重要环节。常见的参数估计方法可以根据是否需要网格搜索,大致分为两大类。一类是免搜索类算法[1–3];另一类是搜索类算法[4–7]。免搜索类算法大多利用旋转不变性[1]获得参数的闭式解,而搜索类算法大多利用信号和噪声子空间的正交性[6,7],然后通过寻找最值估计信源参数。免搜索类算法计算量小但对天线结构有要求,而搜索类算法可应用于任何天线结构但计算量大。
电磁矢量传感器(ElectroMagnetic Vector Sensor, EMVS)是由电偶极子或/和磁环构成的传感器,并且同一个传感器的电偶极子和磁环的数量不会超过3个,单个电偶极子或磁环也可以称为传感器的一个通道[8]。如果按照电偶极子和磁环的中心位置关系划分,可以将EMVS阵列划分成分离式和共点式[8–11]。如果按照EMVS阵列中每个传感器的通道数量划分,可以分成1~6个通道[12–16],其中应用较多的是双电偶极子通道[12,13],3电偶极子通道[14,15]等。EMVS阵列中每个传感器的通道数量较多会造成数据冗余,并且加重系统运算负担。文献[8]首次提出只用6个通道构成的单电磁矢量传感器(Uni-ElectroMagnetic-Vector-Sensor, UEMVS)通过矢量叉积方法就可实现对角度和极化的估计。相比于EMVS阵列,UEMVS由于只需6个通道数据实现对目标参数的估计,极大降低了计算量。但是在研究UEMVS和EMVS阵列的现有文献[8–15]中大多针对传感器内部单元全向模型,并不适用于有向方向图模型,并且单有向电磁矢量传感器(Uni-Direction-ElectroMagnetic-Vector-Sensor, UDEMVS)与UEMVS的最大区别就是内部单元的有向性。
本文建立了UDEMVS的回波模型,然后针对UDEMVS回波模型特点,分别提出了基于免搜索的旋转不变子空间和矢量叉积(Estimation of Signal Parameters via Rotational Invariant Technique and Vector Cross Product, ESPRIT-VCP)方法以及基于网格搜索的多重信号分类和最小瑞利商(MUltiple SIgnal Classification and Minimum Rayleigh Quotient, MUSIC-MRQ)方法。ESPRIT-VCP方法利用旋转不变特性和矢量叉积,在有向方向图模型中找到2维角度和2维极化的闭式解。MUSIC-MRQ方法通过信号和噪声子空间的正交性与最小Rayleigh商问题,结合Rayleigh-Ritz定理[17]得到Rayleigh商最小时的特征值和特征矢量,进而得到2维角度的估计,并利用估计的2维角度结合信号模型得到2维极化参数的估计值。最后仿真验证了所提两种方法在UDEMVS中对角度和极化参数估计的有效性。
2 信号模型
2.1 全局坐标系与局部坐标系的转换
共形UDEMVS阵列的传感器在空间分布上有很大的自由度,但是整个阵列面临着信号被遮蔽[18],全/局坐标转换复杂[19]等问题。共形UDEMVS阵列由依附在共形载体上的多个UDEMVS构成,本节将重点介绍UDEMVS模型面临的全局坐标系和局部坐标系的转换。回波在全局笛卡儿坐标系下的信号模型见图1。
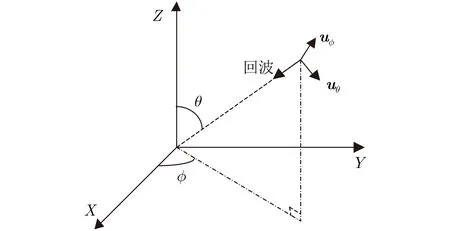
图1 回波信号模型

2.2 单有向电磁矢量传感器信号模型
由UDEMVS构成的共形UDEMVS阵列模型见图3。
图3(a)中Ex−Ey−Ez是 电场分量,Hx−Hy−Hz是磁场分量,图3(b)是以圆环阵为例,N2个UDEMVS与圆环共形的示意图。由于图3(b)中每个传感器有6个通道,导致整个圆环阵列的通道数高达 6N2,系统运算负担大。同时,实际雷达系统在长期工作状态下,难免存在传感器坏损的问题,而图3(b)中通道数较多也增加了传感器坏损的概率。幸运的是,只需要在图3(b)的N2个UDEMVS中选择某个仍可正常工作的UDEMVS接收回波数据就可以实现对回波中信源4维参数的估计,进而有效避免图3(b)的共形阵列中1个或多个传感器的通道坏损时对整个雷达系统参数估计的影响。但是由于每个UDEMVS只能采集6个通道的数据,所以利用UDEMVS采样数据估计信源时的最大信源数不能超过5个[8]。基于此应用背景,本文将重点研究在一个UDEMVS模型下的参数估计问题。UDEMVS的接收信号y(t)可以表示成
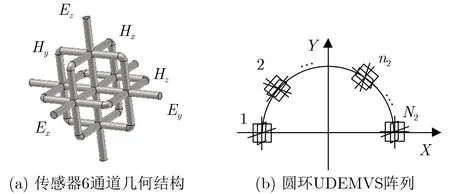
图3 由UDEMVS构成的共形UDEMVS阵列模型
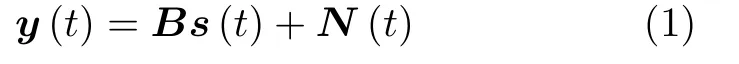
其中,B ∈C6×P是极化-空间导向矩阵,s(t)∈CP×L是回波信号,N(t)∈C6×L是高斯白噪声,P是入射目标数,L是快拍数。回波信号可以表示为s(t)=[s1(t),s2(t),...,sP(t)]T,第p个入射信号为sp(t)=Apej(2πfpt+φp),Ap是 回波幅度,fp是回波频率,φp是 回波初相,1≤p ≤P,[·]T是转置符号。
极化-空间导向矩阵B与角度和极化参数有关[21]。假设目标回波都是完全极化波[21,22], (γ,η)是2维极化参数。极化-空间导向矩阵B可以表示成
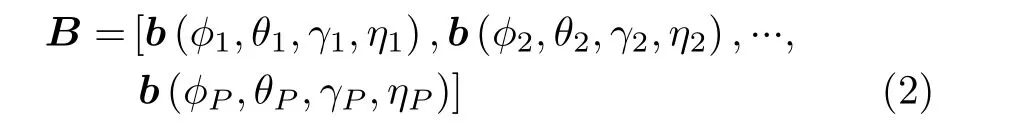
第p个目标的导向矢量b(ϕp,θp,γp,ηp)可以表示成
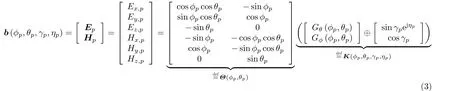
其中,⊕是Hadamard积,Ep和Hp分 别是第p个目标的电场和磁场矢量,Gθ(ϕp,θp)和Gϕ(ϕp,θp)是全局球坐标系下的正交分量,可以通过图2过程得到。式(3)适用于Jones模型[21]表征回波极化的电磁回波,Θ(ϕp,θp)和K(ϕp,θp,γp,ηp)具体形式在式(3)中。为了后文描述方便,Gθ(ϕp,θp)和Gϕ(ϕp,θp)将被分别简写成Gθ和Gϕ,且本文只考虑完全极化电磁回波。
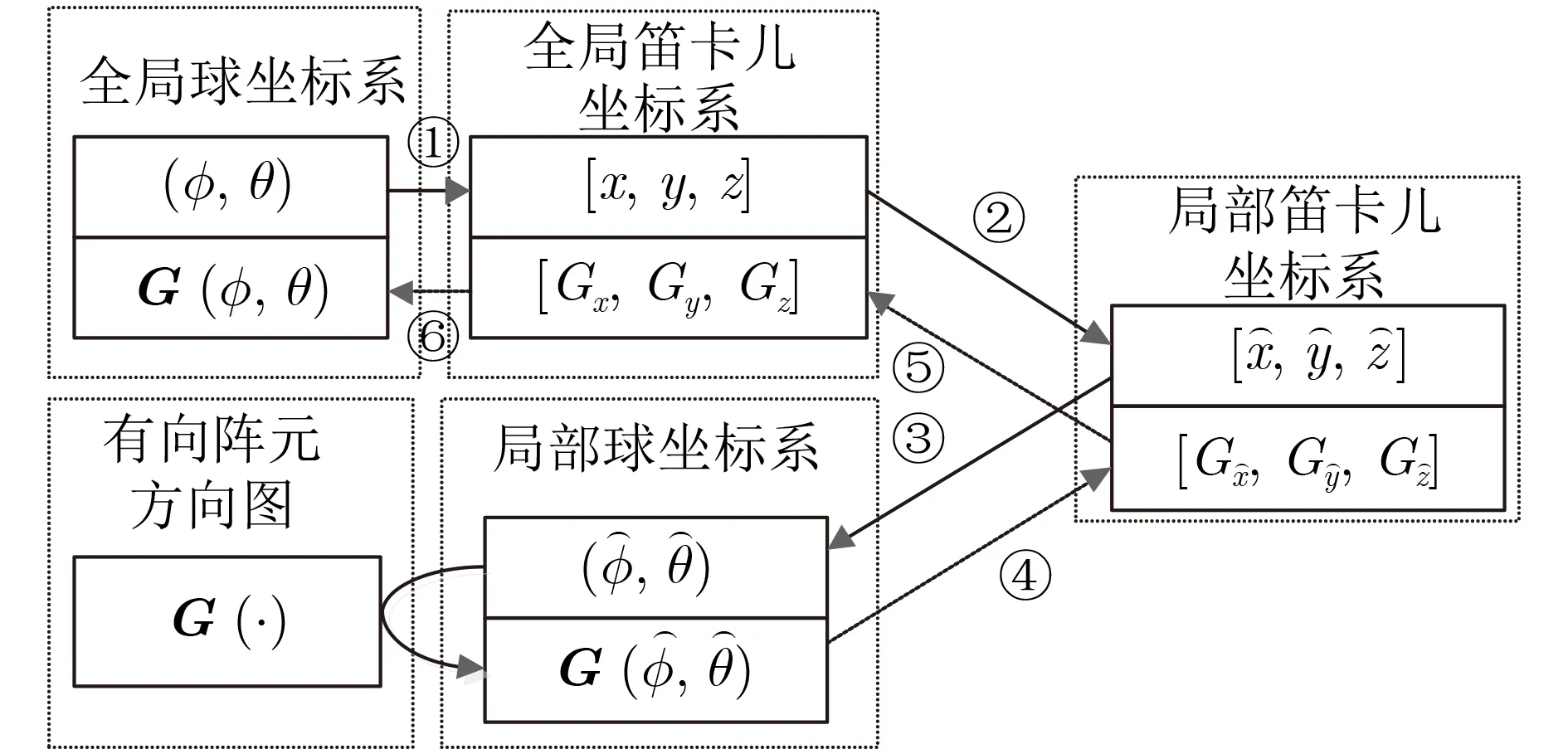
图2 不同坐标系的转换过程
3 所提方法
3.1 ESPRIT-VCP方法的参数估计


对UDEMVS回波进行L次采样得到y(tl),1≤l ≤L。然后间隔时间∆T再进行L次采样得到y(tl+∆T) 。将得到的y(tl) 与y(tl+∆T)组合在一起,得到

令Ψ=T−1ΦT,又由于Es1和Es2可以通过回波采样数据Y(tl)估计出来的,因此可以根据式(7)得到Ψ

其中。[·]†是伪逆符号。然后对Ψ进行特征值分解,可以估计出Tˆ 和Φˆ 。进而得到估计的导向矩阵Bˆ∈C6×P为
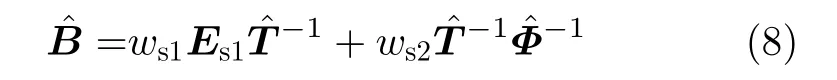
其中。ws1和ws2分别是式(4)两次数据采样对应的加权系数。在现有文献中多采用均匀加权[8],即
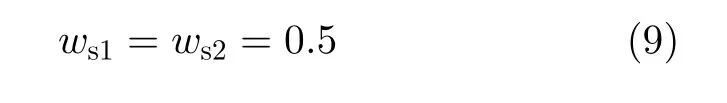
其实对于实际雷达信号处理,两次采样数据y(tl)和y(tl+∆T)的回波信噪比不会完全相同。同时,由于信噪比与估计精度成正比,所以式(8)中Es1Tˆ−1和Tˆ−1Φˆ−1与 实际目标导向矩阵B的近似程度也不同,如果式(8)继续采用式(9)的均匀加权方案,将无法准确地估计导向矩阵Bˆ。幸运的是,可以利用两次采样数据的功率或者目标和噪声的特征值等信息对两次采样的信噪比进行有效估计,进而合理设计式(8)中的权系数。接下来将提出两种有效的加权方案,方案1是基于回波功率的加权方法;方案2是基于特征值的加权方法。基于回波功率的加权方法可以表示成


3.2 MUSIC-MRQ方法的参数估计
在介绍MUSIC-MRQ方法之前简单介绍一下Rayleigh-Ritz定理[17],Rayleigh-Ritz定理可用来解决Rayleigh商的最大最小值问题。假设d是待选择向量,V是Hermite矩阵,V的特征值λ1,λ2,...,λm的大小关系为λmin=λ1≤λ2≤...≤λm=λmax,则根据Rayleigh-Ritz定理,Rayleigh商dHV d/dHd的最大最小值[17]可表示成
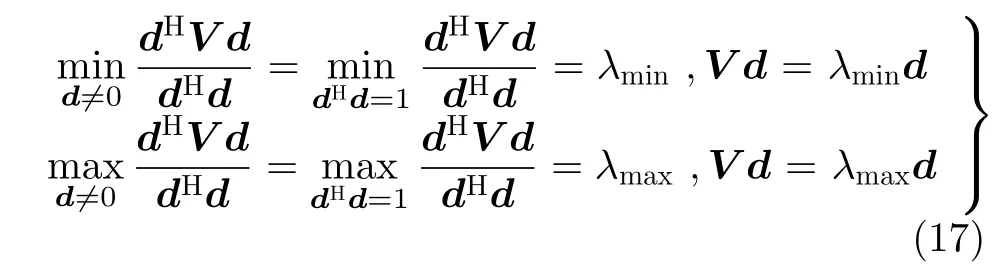
其中,λmin和λmax是 Rayleigh商dHV d/dHd的最小值和最大值。
MUSIC-MRQ方法的主要思路是,通过信号子空间与噪声子空间的正交关系得到谱函数,并将其推导成Rayleigh商的形式,再通过Rayleigh-Ritz定理得到Rayleigh商的最小值。Rayleigh商取最小值时对应的角度就是估计的角度值,然后利用估计的角度和Rayleigh商最小特征值对应的特征向量得到目标2维极化参数估计值。本节信号模型和2.2节相同,UDEMVS的接收信号y(t)的协方差矩阵为

其中, repmGT(ma,mb)表示将矩阵GT中的元素平铺扩展ma行mb列,得到维度为mgama×mgbmb的新矩阵,mga和mgb分别表示矩阵GT的行与列。同时注意到PsHPs=1,因此式(21)可以进一步转变成

MUSIC-MRQ方法通过将式(19)的谱函数巧妙转变成式(23)的形式,进而利用Rayleigh-Ritz定理,实现了只通过2维角度搜索找D(φ,θ)的特征值最小时对应的角度,就可以在角度-极化未知的4维模型中求解出目标的2维角度,然后再利用式(3)中的回波模型关系,计算出2维极化估计值。相比于传统的MUSIC方法,避免了复杂的4维搜索,极大地降低了搜索计算负担。然而MUSIC-MRQ方法本质上属于一种秩亏算法[23,24],并且只用了6个通道的回波数据,因此MUSIC-MRQ方法受快拍和信噪比(Signal-to-Noise Ratio, SNR)的影响明显。
需要注意的是,ESPRIT-VCP方法和MUSICMRQ方法估计极化参数的过程是相同的,只是估计角度参数时两种方法所用思路不同,因此所提两种方法的角度估计结果都会影响对应的极化估计精度。
4 仿真分析
为了分析所提方法的有效性,本节通过仿真实验分析了ESPRIT-VCP方法和MUSIC-MRQ方法的4维参数估计结果,对比了不同方法的分辨概率;散点图;均方根误差(Root Mean Square Error,RMSE)结果。UDEMVS的有向方向图[20]定义为
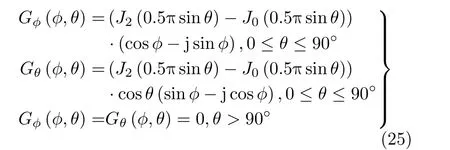
其中,J0(·)是 第1类0阶贝塞尔函数,J2(·)是第1类2阶贝塞尔函数。每个目标的2维角度和2维极化的分辨概率表达式为

假设有两个目标,目标1的4维参数为(25◦,20◦,45◦,60◦),归一化回波频率为0.85,目标2的4维参数为( 50◦,40◦,65◦,105◦),归一化回波频率为0.53,快拍L=1000 , 蒙特卡洛实验次数Mc=100,MUSIC-MRQ方法的搜索间隔为0.01◦,估计的背景噪声功率P˜n ≈0.9962。
假设ESPRIT-VCP方法中式(4)两次采样数据y(tl) 和y(tl+∆T) 的信噪比差值为∆,即∆=SNRy(tl+∆T)−SNRy(tl)。 在图4中验证了在∆=4 dB和∆∈U[−4,4] dB条件下,式(9)—式(11)中不同加权方案对ESPRIT-VCP方法估计性能的影响,其中U[−4,4]表 示服从[−4,4]的均匀分布且横坐标是数据y(tl)的SNR。
图4中,ESPRIT-VCP方法与式(9)—式(11)结合其实就是采用了不同的加权方案。当∆=4时,E S P R I T-V C P 方法的整体估计性能要比∆∈U[−4,4]好 ,不过∆∈U[−4,4]更符合实际情况。从图4可知,不管是2维角度还是2维极化,ESPRITVCP-(9)的性能最差,说明均匀加权方案并不是最优的权系数解决方案。在SNR> 5 dB时,ESPRITVCP-(10)与ESPRIT-VCP-(11)方法的RMSE结果相差不超过0.01°,同时考虑到ESPRIT-VCP-(10)更适合工程应用,而ESPRIT-VCP-(11)方法的加权方案涉及奇异值分解,运算量大,所以后续将以ESPRIT-VCP-(10)方法代表在3.1节的所提方法。
新一轮后勤改革完成后,华中师范大学形成了以分管校领导亲自抓、部门主要负责人直接抓的层层落实责任制,全面落实食品安全应急处置机制,实施食品安全责任追究机制。通过建章立制形成科学、高效、规范、有序的工作机制,制定《食品安全工作站成员工作职责》、《食品安全工作流程》、《食品安全应急处置预案》、《二次供应管理细则》,涉及信息报送、日常巡查、绩效体系考评、突发事件应急处置、监管户档案管理等。
在图5中展示了S NR=20 dB且∆∈U[−4,4] dB时2维角度和2维极化的估计结果散点图。
图5中,ESPRIT-VCP-(10)相比于MUSIC-MRQ而言,目标1和目标2的2维角度RMSE结果分别提高了约0.16°和0.26°;目标1和目标2的2维极化RMSE结果分别提高了约0.51°和0.79°。可从两方面解释ESPRIT-VCP-(10)估计精度优于MUSICMRQ的原因,一方面是,ESPRIT-VCP-(10)方法需要两次采样过程且每次采样L个快拍,而MUSIC-MRQ方法只需要1次采样过程,所以ESPRITVCP-(10)需要更多的快拍数据;另一方面是,MUSIC-MRQ属于秩亏算法且通道数只有6个,再加上极化估计精度受角度估计结果的影响,所以MUSIC-MRQ不管是角度还是极化的估计结果都比ESPRIT-VCP-(10)方法差。
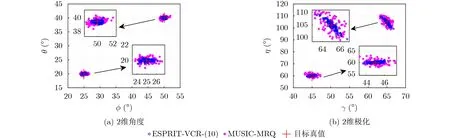
图5 参数估计散点图
图6和图7分别展示了所提两种方法的分辨概率和RMSE随SNR变化的结果,其中∆∈U[−4,4] dB。
随着SNR的增加,MUSIC-MRQ方法与ESPRIT-VCP-(10)的估计偏差越来越小,但是两种方法对2维极化的估计都需要用到2维角度的估计值,所以在图6和图7中2维极化的估计偏差都大于对应的2维角度。
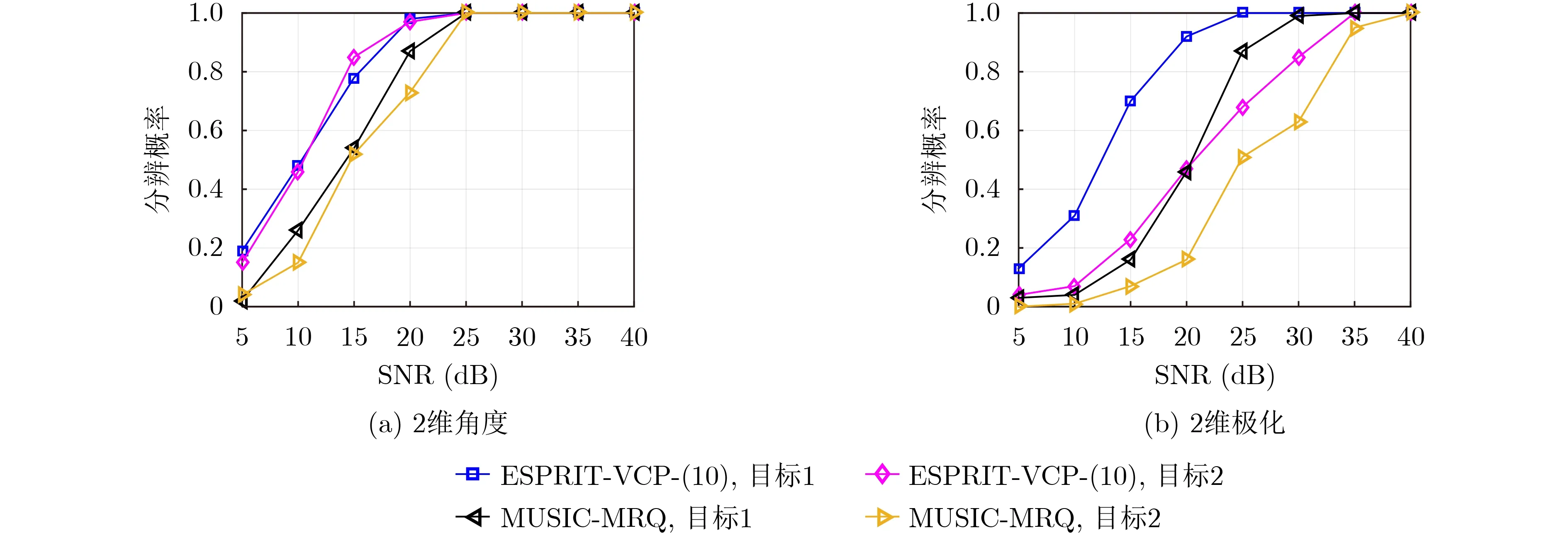
图6 分辨概率随SNR变化的结果,其中分辨门限∆ϕ =∆θ =∆γ =∆η =1◦
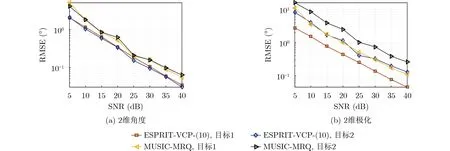
图7 RMSE随SNR变化的结果
图8展示了 S NR=20 dB 且∆∈U[−4,4] dB时,所提的两种方法随快拍变化的RMSE结果。
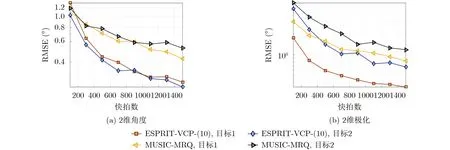
图8 RMSE随快拍变化的结果
从图8可以看到,不管是ESPRIT-VCP-(10)还是MUSIC-MRQ,RMSE受快拍的影响还是很明显的。这是因为它们都需要对协方差矩阵进行奇异值分解,而协方差矩阵是通过极大似然估计过程得到的,因此当快拍越多时,奇异值分解后得到的信号子空间和噪声子空间才更准确。
从图5—图8可看到,MUSIC-MRQ方法的整体估计性能比ESPRIT-VCP-(10)方法差,并且ESPRIT-VCP-(10)由于不需要网格搜索,所以计算复杂度比MUSIC-MRQ方法小。但ESPRITVCP-(10)方法只能应用于UDEMVS模型中,而MUSIC-MRQ方法可以应用于共形UDEMVS阵列中。需要注意的是,在第4节的仿真实验中,MUSIC-MRQ方法的整体估计性能较差除了因为MUSIC-MRQ是一种秩亏算法外,另外一个原因是所用模型的通道数太少,如果将MUSIC-MRQ方法应用到通道数足够多的共形UDEMVS阵列中,MUSIC-MRQ方法的估计性能会有显著提升。
5 结束语
本文考虑到共形UDEMVS阵列的通道数较多,长时间工作后部分通道容易出现坏损的情况影响参数估计的性能,提出了两种只需利用一个正常工作的UDEMVS的采样数据实现信源参数估计的方法,分别是ESPRIT-VCP方法和MUSIC-MRQ方法,并对ESPRIT-VCP提出了两种工程有效的加权方案。根据第4节UDEMVS的仿真结果,可看到ESPRIT-VCP的参数估计性能比MUSIC-MRQ好,并且ESPRIT-VCP的计算复杂度比MUSICMRQ低,但是MUSIC-MRQ适用面更广,不仅可以应用到UDEMVS模型中,也可以应用于共形UDEMVS阵列中。
然而,不管是ESPRIT-VCP方法还是MUSICMRQ方法,极化参数的估计都需要先估计出角度参数,导致角度估计误差直接影响极化参数的估计精度。后续将对如何提高极化参数的估计精度展开进一步研究。

