冲击荷载下白云岩块度分布及分形特征*

秦 梨，邓 涛，张成良，廖元欢，周 成

(昆明理工大学 国土资源工程学院，云南 昆明 650093)

0 引言

露天矿山开采的主要工序是台阶爆破[1-3]。单孔药量的选择会直接影响爆破的质量，台阶爆破过程中，越靠近炮孔的位置，加载应变率越高。应变率直接反映岩石变形和破碎的程度[4-6]，因此，研究岩石在给定应变率范围内的响应特征，实现炸药用量与岩石破碎块度的合理匹配，可为优化台阶爆破施工参数提供依据，对改善岩石爆破效果、降低爆破作业成本具有重要意义。

为了研究岩石在高应变率下的动力响应特征，一些学者将分离式霍普金森压杆(SHPB)实验装置应用于爆破领域。WANG等[7-9]对SHPB在爆破领域的实用性进行了初探。代仁平等[10-12]利用φ100 mm的SHPB对隧道围岩进行了损伤防护试验，从应力波衰减、试件宏观破坏和能量变化等方面进行了定量分析。杨立云等[13]通过焦散线实验系统和SHPB动静组合加载装置，在亚克力模型中施加爆炸动态载荷和初始静态应力场，探讨了不同切槽角度(0°、45°和90°)下初始应力场对爆炸后碎块裂纹扩展的影响规律。蒲传金等[14-15]利用一级轻气炮开展了岩石的冲击损伤实验，并对冲击后的试件进行了损伤测试，根据宏-细观观测结果研究了损伤特性与声波速率变化的关系。杨东辉等[16]利用改进的SHPB系统研究了堵塞器和黏土炮泥在动态载荷下的力学特性。郭浩等[17]通过大量的理论计算和冲击试验，总结了SHPB在爆破实验中的应用效果，进一步验证了SHPB在爆破领域的实用性。

目前的研究主要聚焦于岩石的动力学响应与破坏形态等方面，对不同应变率下试件分形特征与细观裂纹扩展的研究较少。本文利用SHPB对现场所取岩样进行动力压缩试验，探究了白云岩在不同应变率下的应力-应变曲线和破碎特征，通过直接筛分的方法，分析了在不同应变率下试件的破碎块度分布与分形特征。

1 试验准备

1.1 试样制备

白云岩试样取自四川攀枝花某露天采石场，选择完整、均质的岩样作为研究对象。根据国际岩石力学学会(ISRM)的试验要求，试样尺寸定为φ50 mm×50 mm。对岩样两个端面分别打磨、抛光，使其不平整度小于0.02 mm[18]。部分试样见图1。试样的静态物理力学参数见表1。

表1 试样的静态物理力学参数Table 1 Static physical and mechanical parameters of the sample

1.2 试验装置及原理

利用昆明理工大学爆破实验室现有的SHPB试验装置(见图2)对试样开展单轴冲击试验，试验装置主要由压杆系统、加载装置、数据采集系统以及测速装置组成。压杆系统包括缓冲杆、透射杆、入射杆，长度分别为500、2 000、2 000 mm，均由Cr40制成，其弹性模量均为210 GPa，纵波波速为5 190 m/s。有研究[19]表明，采用纺锤形子弹可以实现恒应变率加载。

图1 部分白云岩试样Fig.1 Part of the dolomite sample

图2 试验装置Fig.2 Testing device

试验原理是：在动力源的驱动作用下，子弹撞击入射杆并在杆内形成入射波，入射波传至入射杆与试样的交界处，一部分应力波穿过试样进入透射杆形成透射波，另一部分入射波发生反射进入入射杆形成反射波。反射波、透射波和入射波信号由安装在压杆上的应变片获得。

(1)

式中，C0、E0分别为压杆波速和弹性模量，Ls为试样长度，A0、As分别为压杆和试样的横截面积，εI(t)、εR(t)、εT(t)分别为测得的入射、反射、透射应变信号。

SHPB试验基于一维假定和应力均匀性假定。为了满足一维假定，试验过程中压杆与试样之间需要紧密接触。为了满足应力均匀假定，试验前需要进行应力平衡检验。试样两端的动态应力平衡图见图3。由图3可知，试验过程中试样两端受力大致相等，满足平衡条件[21-22]。冲击压缩试验前需确定冲击气压。以 0.4 MPa 的冲击气压试冲了2次，试样未发生宏观破坏；再用 0.5 MPa的冲击气压试冲，试样发生破坏，且示波器显示的波形较好。因此，选择冲击气压为0.5、0.6、0.7、0.8、0.9 MPa，各种气压冲击3次以减小误差。

图3 动态应力平衡图Fig.3 Dynamic stress equilibrium diagram

2 结果分析

冲击压缩试验结果见表2。

表2 冲击压缩试验结果Table 2 Impact compression test result

2.1 应力-应变曲线及破坏形态分析

不同应变率下的试样应力-应变曲线见图 4。

图4 应力-应变曲线Fig.4 The curve of stress-strain

由图4可知，试样的应力-应变曲线可分为裂隙闭合阶段、弹性阶段、塑性变形阶段和峰后软化阶段。在裂隙闭合阶段，曲线微凹，试样内部的裂隙被压实，曲线斜率逐渐增大。在弹性阶段，将试样视为弹性体，应力与应变大致呈线性关系，内部的弹性应变能逐渐积聚，试样未发生宏观损伤。超过弹性极限后曲线进入塑性变形阶段，表现出应变软化特征，斜率减小，试样内储存的弹性应变能得到释放，有少量微裂隙产生，原有裂隙扩张，损伤不断累积。当曲线进入峰后软化阶段后，损伤达到极限，试样发生宏观破裂[23]。

试样的峰值应力与峰值应变随平均应变率的变化如图5所示。由图5可知，随着应变率的增加，峰值应力不断增大，说明试样的峰值应力对于应变率有较强的依赖性。这是因为瞬态载荷作用下，试样没有足够时间去积累能量，所以通过增大内部应力的方式补偿试样内部冲量的变化，致使材料内部产生了更多的微裂纹，试样的破坏程度加剧。由图5还可以看出，随着应变率的增加，试样的峰值应变逐渐减小，说明其抗变形能力逐渐减弱，更易破坏。

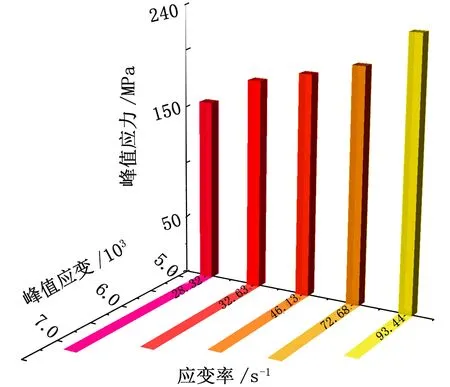
图5 峰值应力与峰值应变随应变率的变化曲线Fig.5 Curves of peak stress and peak strain varied with strain rate

2.2 破坏块度分布特征

采用直接测量法筛分破坏后的岩石块度，将平均粒径 δ 作为试样的破坏评价指标。利用分级筛筛分，孔径由小到大依次为1.0、2.0、5.0、10.0、15.0 mm。粒径范围设置为15.0～50.0、10.0～15.0、5.0～10.0、2.0～5.0、1.0～2.0、0～1.0 mm，各粒径范围记为i(i=1～6)，将不同碎块的最大与最小粒径的平均值作为平均粒径(δ)。

块度分析的主要步骤为：①用分级筛筛分碎块，使用高精度电子秤测量碎块质量(mi)；②由碎块质量(mi)和总质量(m)得出碎块质量分数(ηi)；③将质量分数(ηi)乘以对应粒径的平均粒径(Ri)，得到该粒径在所有碎块中的比例(δi)；④将碎块粒径质量分数叠加，得到平均粒径。计算式[24]分别为

(2)

(3)

根据式(2)、式(3)可获得不同冲击荷载作用下的试样碎块质量分数与平均粒径，计算结果见表3 。

表3 试样破坏后的块度分布特征Table 3 Block size distribution characteristics of testing sample after breakage

冲击荷载下粒径分布及尺寸变化规律如图6所示。由表 3和图6可知，随着应变率的变化，试样破碎粒径和粒径尺寸的变化呈现出了一定的规律。应变率由从28.32 s-1增至 93.44 s-1时，最大粒径(≥15.0 mm)碎块质量分数从92.17%降至 5.37%，降幅为 94.17%；而粒径在10.0～15.0、5.0～10.0、2.0～5.0、1.0～2.0、0～1.0 mm的质量分数均随应变率的增加而增大；粒径范围不同，其碎块质量分数不同，具体表现为：当粒径在10.0～15.0 mm范围内时，碎块质量分数从3.76%增至 15.37%；当粒径在5.0～10.0 mm范围内时，碎块质量分数由0.23%增至29.14%；当粒径在2.0～5.0 mm范围内时，碎块质量分数由2.65%增至19.37%；当粒径在1.0～2.0 mm范围内时，碎块质量分数由0.24%增至21.14%；当粒径在0～1.0 mm范围内时，碎块质量分数由0.95%增至9.61%。随着冲击气压的增大，岩样破碎平均粒径呈逐渐减小的趋势，说明试样的破坏程度不断增大。应变率由28.32 s-1增至93.44 s-1，平均粒径由30.54 mm减至6.90 mm，减幅为 77.41%。

图 6 冲击荷载下粒径分布及尺寸变化规律Fig.6 The particle size distribution and the size change under impact loads

2.3 试样破碎分形特征

针对岩石破碎后的自相似性，谢和平[25]引入了分形理论。分形维数可以定量地描述冲击过程中试样的破碎程度。利用筛分获得的不同粒径下的碎块质量和质量-等效粒径模型计算分形维数D，计算式[26]为

(4)

D=3-k,

(5)

式中，k为直线的斜率，MT为碎块累计质量，M为试样总质量。计算得到的不同应变率下试样碎块累积质量及分形维数见表4。

表4 不同应变率下试样碎块累积质量及分形维数Table 4 Accumulated mass and fractal dimensions of testing sample at different strain rate

根据表4绘制了不同应变率下lg(MT/M)-lgR曲线(见图7)。由图7可知，直线拟合的数据相关性较好，说明试样在冲击压缩后的破碎分布具有较好的相似性。这是因为裂隙族的集中导致试样宏观破碎，小裂隙族又由更小裂隙族演化聚集，这种自相似性必然会产生具有自相似特征的块度碎片[27]，因此可以用分形维数来定量描述试样在冲击作用下的破碎程度。

图7 不同应变率下lg(MT/M)-lgR 曲线Fig.7 The curve lg(MT/M)-lgR at different strain rate

将各应变率下lg(MT/M)与lgR关系的斜率代入式(5)便可得到试样破坏后的碎块分形维数。分形维数随应变率的变化曲线见图8。由图8可知：分形维数随着应变率的增加近似呈线性增大；当应变率从28.32 s-1增至93.44 s-1时，分形维数由1.69增至2.42，增幅为43.20%；分形维数与试样破碎程度呈正相关，表明随着应变率的增加，分形维数逐渐增大，试样的破碎程度加剧，分形维数的变化在一定程度上反映了试样内部的性质变化[28]。

图 8 分形维数随应变率的变化曲线Fig.8 The curve of fractal dimensions vs. strain rate

表 5为不同应变率下不同碎块的分布特征。图9为不同粒径质量分数随应变率的变化曲线。由图9可知：随着应变率的增加，大粒径碎块质量分数呈线性下降趋势，中粒径及小粒径碎块质量分数呈线性升高趋势；当应变率从28.32 s-1增至 93.44 s-1时，大粒径碎块质量分数由92.17%降至5.37%，中粒径碎块质量分数由6.64%升至63.88%，小粒径碎块质量分数由1.19%升至30.75%，

表5 各应变率下试样碎块的质量分数 单位：%Table 5 The content of broken pieces of testing sample at different strain rate Unit：%

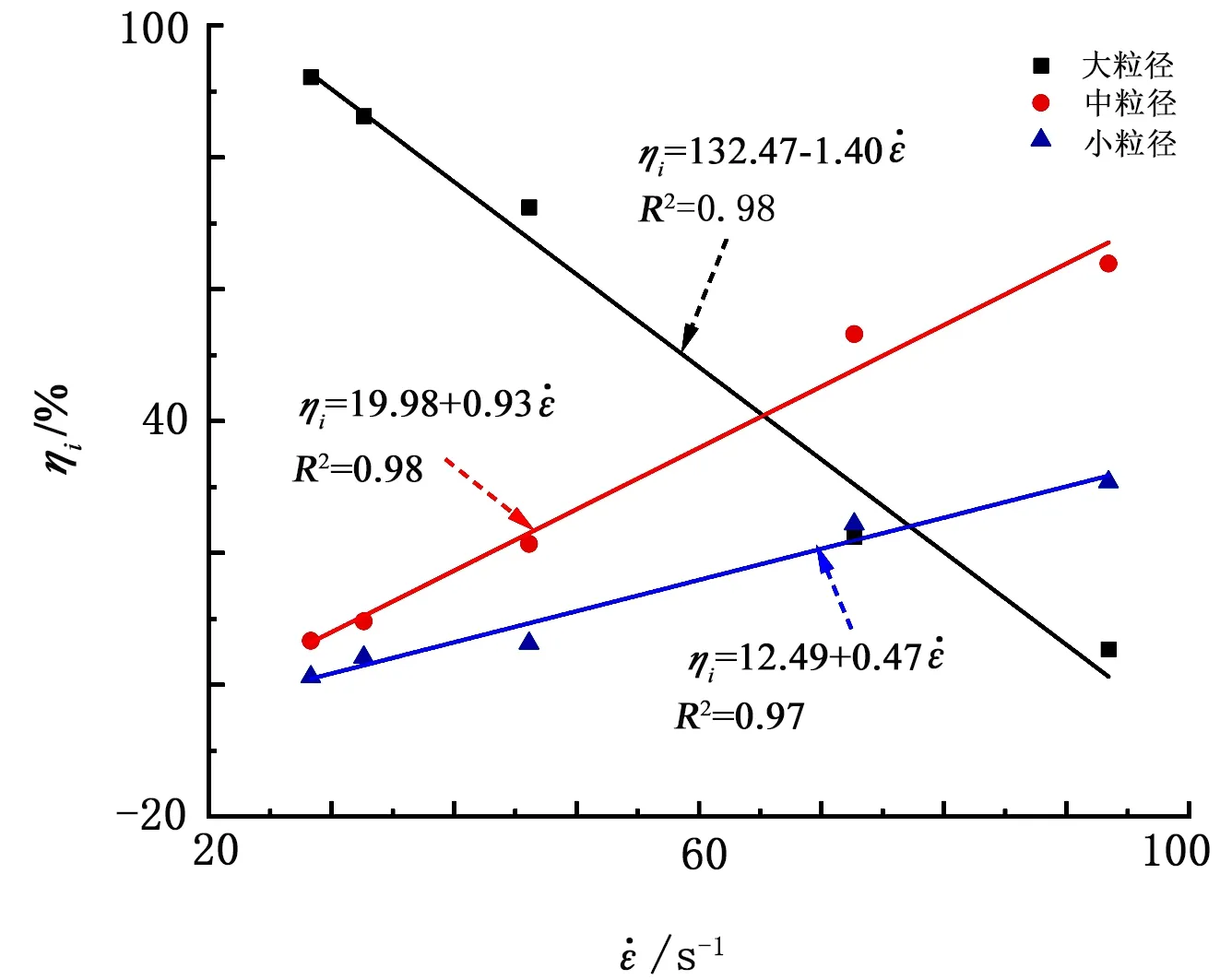
图 9 不同尺度碎块质量分数随应变率的变化曲线Fig.9 The curve of mass fraction of broken pieces with different particle size as a function of strain rate

3 结论

利用分离式霍普金森压杆系统对5种冲击气压(0.5、0.6、0.7、0.8、0.9 MPa)作用下的白云岩试样进行了冲击压缩试验，研究了白云岩在5种不同应变率下(28.32、32.63、46.13、72.68、93.44 s-1)的应力应变特性及破坏特征，采用筛分法求得块度分布特征，利用分形维数对试样的破碎程度进行了定量描述，得到以下主要结论：

a.随着应变率的增加，试样的破坏范围由边缘向中心扩展，破碎块度由大块过渡为小块及粉末，破碎试样的平均粒径随应变率的增加而减小。

b.分形维数随着应变率的增加呈近似线性增大，当应变率由28.32 s-1增至 93.44 s-1时，分形维数由1.69 增至2.42，增幅为43.20%。

c.大粒径碎块质量分数随应变率的增加而降低，中粒径和小粒径质量分数随应变率的增大而升高。